本文考虑如下边值问题$L\left( {p, q, h} \right)$:

其中$\rho$为谱参数, $h$为实数, $p\left( x \right), q\left( x \right)$为实值函数, 且$p\in L^1(0, 1), q\in C[0, 1]$. 边值问题$L\left( {p, q, h} \right)$源于量子力学中的粒子互相碰撞问题, ${\rho ^2}$表示粒子的能量, $p\left( x \right), q\left( x \right)$称为势函数^[1]. 当$p\left( x \right) = 0$时, 方程(1.1)–(1.2) 即为经典的Sturm-Liouville问题^[2-5]. 对于方程(1.1), 经典的逆谱问题旨在由其谱信息(如: 两组谱、Weyl函数, 或者一组谱和部分势函数信息等)重构算子的系数^[6-9]. Buterin和Yurko研究了方程(1.1) 在Dirichlet边界条件的逆谱问题, 并给出了由相应的谱信息重构势函数的算法^[6]. 王於平、杨传富、黄振友以及Koyunbakan和Panakhov等学者研究了相关的半逆问题和逆结点问题^[7-10]. 本文将研究边值问题$L\left( {p, q, h} \right)$基于一类特殊特征值的逆谱问题, 即考虑无穷个具有不同边界条件的边值问题, 从每一个边值问题中抽取第$n$个特征值, 以其组成的谱数据来重构方程(1.1) 中的势函数. 这种思想最早是由McLaughlin和Rundell给出的^[2] (后被称为McLaughlin-Rundell问题), 他们研究了带有边界条件

的Sturm-Liouville方程, 证明了一类特殊的谱集合$\left\{ {{\lambda _n}\left( {q, {H_k}} \right)} \right\}_{k = 1}^{ + \infty }$可以唯一确定势函数$q\left( x \right)$, 其中$n$是固定的, ${H_k}\left( {k \ge 1} \right)$是不同的实数. 对于方程(1.1), 王於平首先研究了带有如下边界条件的McLaughlin-Rundell问题^[10]

并且证明了唯一性定理, 然而从该唯一性定理中并不能获得相应的重构算法. 受到文献[6] 和[10]的启发, 本文将研究边值问题$L\left( {p, q, h} \right)$的McLaughlin-Rundell问题, 并且给出一种比文献[10] 更为简单的唯一性定理证明, 而且我们的证明中还蕴含了重构势函数的算法.

本文约定${\Bbb Z}$为整数集, ${\Bbb N}$为正整数集, ${\Bbb R}$为实数集, ${\Bbb C}$为复平面.

设$\varphi \left( {x, \rho } \right)$为方程(1.1) 满足$\varphi \left( {1, \rho } \right) = 0, \;\varphi '\left( {1, \rho } \right) = 1$的解. 由文献[6] 知, 对于固定的$x \in [0, 1]$, $\varphi \left( {x, \rho } \right)$和$\varphi' \left( {x, \rho } \right)$为$\rho$的整函数, 并且对于充分大的$|\rho|$, 有

其中

记

易知$\Delta \left( \rho \right)$的零点即为边值问题$L\left( {p, q, h} \right)$的特征值, 将(2.1)–(2.2) 式代入(2.3) 式得: 当$\rho\to\infty$时, $\Delta \left( \rho \right)$有如下渐近估计

由标准的方法^{[2, p9]}, 利用Rouché 定理及(2.4) 式知$\Delta \left( \rho \right)$有无穷多个零点, 记为

其满足如下渐近性

记

这是$\rho$的亚纯函数, 被称为Weyl函数. 注意到$\varphi '(0, \rho)$与$\varphi (0, \rho)$不可能同时为零, 所以$M(\rho)$的极点即为$\varphi (0, \rho)$的零点, 记$\varphi (0, \rho)$的零点为${\left\{ {{\mu _k}} \right\}_{\left| k \right| \in{\Bbb N}}}$, 其重数为$m_k$. 由文献[6] 知

其中${M_{k + {m_k} - 1}} \ne 0$, $M_k^0\left( \rho \right)$为$M\left( \rho \right)$在$\mu_k$展开的正则部分, 序列${\left\{ {{M_n}} \right\}_{\left| n \right| \in {\Bbb N}}}$称为Weyl序列.

Buterin和Yurko证明了Weyl函数$M(\rho)$可以唯一确定势函数$p(x)$和$q(x)$, 并且给出了由谱数据${\left\{ {{M_n}, {\mu _n}} \right\}_{\left| n \right| \in {\Bbb N}}}$重构$p(x)$和$q(x)$的算法^[6].

本节将给出唯一性定理和重构算法.对于边值问题$L\left( {p, q, h} \right)$, 我们考虑另一个边值问题$L\left( {\tilde{p}, \tilde{q}, h} \right)$. 本文约定：若$\delta$表示$L\left( {p, q, h} \right)$的物理量, 则$\tilde{\delta}$表示$L\left( {\tilde{p}, \tilde{q}, h} \right)$相应的物理量.

选择序列${\left\{ {{h_k}} \right\}_{k \in {\Bbb N}}}$满足

其中$C\in {\Bbb R}.$

定理3.1 (唯一性)    设序列${\left\{ {{h_k}} \right\}_{k \in {\Bbb N}}}$满足(3.1) 式, 若对某个固定的$n\in {\Bbb Z}$有

则$p\left( x \right) \mathop = \limits^{a.e.} \tilde p\left( x \right), q\left( x \right) = \tilde q\left( x \right), x\in [0, 1].$

引理3.1    设${\left\{ {{h_k}} \right\}_{k \in {\Bbb N}}}$满足(3.1)式, 则${\left\{ {{\rho _n}\left( {p, q, {h_k}} \right)} \right\}_{n \in {\Bbb Z}}} \cap {\left\{ {{\rho _n}\left( {p, q, {h_{k + 1}}} \right)} \right\}_{n \in {\Bbb Z}}} = \emptyset .$

引理3.1的证明可参考文献[10] 中引理2.1. 结合(2.5) 式及引理3.1, 我们得到如下引理.

引理3.2   对于任意固定的$n\in {\Bbb Z}$, 谱集合$\left\{ {{\rho _n}\left( {q, p, {h_k}} \right)} \right\}_{k = 1}^\infty$是一个有界无穷数集.

引理3.3^[11]   设$f_1(z)$和$f_2(z)$为整函数, ${\left\{ {{z_n}} \right\}_{n \ge 1}}$为有聚点的序列. 若${f_1}\left( {{z_n}} \right) = {f_2}\left( {{z_n}} \right)$, $n\in {\Bbb N}$, 则${f_1}\left( z \right) = {f_2}\left( z \right), \;z \in {\Bbb C}$.

证   文献[6] 已经证明：若$M(\rho ) = \tilde M(\rho )$, 则$p\left( x \right) \mathop = \limits^{\rm a.e.} \tilde p\left( x \right), q\left( x \right) = \tilde q\left( x \right).$下面我们仅需证明: 若(3.2) 式成立, 则$M(\rho ) = \tilde M(\rho )$. 固定$j_1\in {\Bbb Z}$, 记$\rho _k^{{j_1}}: = {\rho _{{j_1}}}(p, q, {h_k}), k \in {\Bbb N}$. 由$M(\rho )$的定义知

类似地, 也有

结合(3.3) 和(3.4) 式得

记

则${f_1}\left( \rho \right)$和${f_2}\left( \rho \right)$为整函数. 由引理3.2知, ${\big\{ {\rho _k^{{j_1}}} \big\}_{k \in {\Bbb N}}}$为有界无限点集, 所以必有聚点. 因此, 由引理3.3知${f_1}\left( \rho \right) = {f_2}\left( \rho \right), \;\rho \in {\Bbb C}.$结合$M(\rho )$和$\tilde M(\rho )$的定义得

证毕.

下面考虑对应于定理3.1的重构算法. 文献[6] 已经给出由序列${\left\{ {{M_k}} \right\}_{{\rm{|}}k{\rm{|}} \in {\Bbb N}}}$和${\left\{ {{\mu _k}} \right\}_{{\rm{|}}k{\rm{|}} \in {\Bbb N}}}$重构$p(x)$和$q(x)$的算法, 我们仅需给出由${\left\{ {{\rho _{{j_1}}}\left( {q, p, {h_k}} \right)} \right\}_{k \in {\Bbb N}}}$和${\left\{ {{h_k}} \right\}_{k \in {\Bbb N}}}$重构序列${\left\{ {{M_k}} \right\}_{{\rm{|}}k{\rm{|}} \in {\Bbb N}}}$和${\left\{ {{\mu _k}} \right\}_{{\rm{|}}k{\rm{|}} \in {\Bbb N}}}$的算法即可. 为此我们需要如下引理.

引理3.4   如果$R>0$是如下幂级数的收敛半径

则$f(z)$在$\left\{ {z:\left| {z - {z_0}} \right| < R} \right\}$上解析, 并且在$\left\{ {z:\left| {z - {z_0}} \right| = R} \right\}$上至少存在一个奇点.

因为两集合${\left\{ {{h_k}} \right\}_{k \in {\Bbb N}}}, {\big\{ {\rho _k^{{j_1}}} \big\}_{k \in {\Bbb N}}}$有界并且无限, 所以存在聚点(分别记为$h_*, \rho_*$)满足

令

由(3.3)、(3.5) 和(3.6) 式知$a_n\;(n\ge 0)$为$M(\rho)$的Taylor系数, 因此

其中$R_*>0$为级数(3.7) 的收敛半径, 且

利用幂级数解析延拓法对$M(\rho)$进行解析延拓. 由引理3.4知, $M(\rho)$在

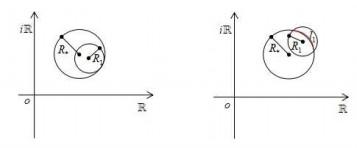
上至少存在一个(至多有限个^[6])极点. 下面确定$M(\rho)$在${\Omega _*}$上的极点. 在$D_1$内任取一点${\rho _{1{\rm{*}}}}$, 将$M(\rho)$在${\rho _{1{\rm{*}}}}$处Taylor展开, 则存在一个收敛半径$R_1$, 使得级数(3.7) 在${D_2} = \left\{ {\rho: \left| {\rho - \rho _{1*}} \right| < {R_1}} \right\}$内收敛. $D_1$和$D_2$有两种情况:

1. 内切;

2. 相交(如图 1所示).

若内切, 则由引理3.4, 说明切点为极点. 若是第二种情况, 则$M(\rho)$在$D_2$内的一段弧$l_1$上(不包括端点) 无极点, 此时可以令$\rho$从$D_1$内趋于弧$l_1$的两个端点, 观察$M(\rho)$是否趋于无穷来判断这两个端点是否为$M(\rho)$的极点. 这样可以通过在$D_1$内选择有限个点, 将$M(\rho)$在这有限个点处Taylor展开, 从而找出$M(\rho)$在$\Omega_*$上的所有极点$\left\{ {\rho _{1k}} \right\}_{k = 1}^{{N_1}}$.

下面来确定每个极点的阶数. 注意到, $M(\rho)$的任意一个极点, 虽然不一定是简单极点, 但一定是有穷极点. 利用公式

通过取$m = 1, 2, \cdots$来判断极点的阶数. 若${c_{ - m}} = \infty$, 则$m$的值需要继续增加; 若$c_{-m}$为非零常数, 则$\rho_{1k}$为$m$阶极点.

设$\rho_{1k}$的阶数为$m_{1k}\;(k = 1, 2, \cdots , {N_1})$, 则利用公式(2.6) 得到$\left\{ {\rho _{1k}^{}} \right\}_{k = 1}^{{N_1}}$所对应的Weyl序列

由已找到的$M(\rho)$的极点$\rho_{1k}$及其重数$m_{1k}\;(k = 1, 2, \cdots , {N_1})$, 构造函数

显然函数$M_1(\rho)$在$\Omega_*$上解析. 在$D_1$内找一点$z_1\;(z_1\ne \rho_*)$, 将$M_1(\rho)$在$z_1$处Taylor展开得

其中

对函数$M_1(\rho)$重复上面$M(\rho)$的步骤(此时在$D_3\setminus D_1$内选择有限个点), 可以获得$M_1(\rho)$在$D_3$边界上的极点及其重数, 然后再次利用公式(2.6) 获得对应的Weyl序列. 这样一直进行下去可以得到Weyl函数$M(\rho)$的所有极点及Weyl序列, 然后运用文献[6] 中的方法可以重构出$p(x)$和$q(x)$.

对上述由序列${\left\{ {{\rho _{{j_1}}}(p, q, {h_k})} \right\}_{k \in {\Bbb N}}}$和${\left\{ {{h_k}} \right\}_{k \in {\Bbb N}}}$重构势函数$p(x)$和$q(x)$的算法总结如下:

第1步: 定义集合${\left\{ {{\rho _{{j_1}}}(p, q, {h_k})} \right\}_{k \in {\Bbb N}}}$到集合${\left\{ {{h_k}} \right\}_{k \in {\Bbb N}}}$的映射, 记为$M(\rho)$;

第2步: 从上述两个集合中分别选取聚点$\rho_*$和$h_*$, 满足(3.5) 式;

第3步: 构造幂级数(3.7), 其中$a_n$由(3.6) 式给出, $R_*$由(3.8) 式给出;

第4步: 运用上述的幂级数解析延拓法找到Weyl函数$M(\rho)$的所有极点和Weyl序列;

第5步: 应用文献[6] 中的方法重构$p(x)$和$q(x)$.