无界算子在应用偏微分方程求解问题, 弹性力学、流体力学等数学物理问题中有重要的应用, 因此, 无界算子的谱性质及谱分布的研究受到了国内外诸多学者的广泛关注^[1-2].在谱性质及谱分布的研究中, 较为常用的方法有谱函数、Schur补分解、数值域、二次数值域和Gershgorin定理等, 其中二次数值域是刻画算子的谱分布范围的有效工具.

1998年, Tretter和Langer^[3]首次提出了二次数值域的概念, 并利用二次数值域对分块算子矩阵的谱范围进行了估计.二次数值域是数值域的一个子集, 它不一定是凸集, 且至多由两个连通区域构成.对于有界算子而言, 二次数值域的闭包包含其谱, 但对于无界算子而言, 二次数值域只能无条件的包含其点谱, 二次数值域的闭包也不一定能包含其近似点谱. 2001年, Langer, Markus和Matsaev^[4]研究了$2\times2$阶分块算子矩阵的二次数值域, 谱包含性质及Schur补的分解定理. 2004年, Kraus和Langer等人^[5]利用二次数值域研究了三类无界块分块算子矩阵的性质, 建立了无界分块算子矩阵特征值的变分原理, 并给出了特征值估计的渐近公式.对于无界分块算子矩阵${\cal A} = \left[\begin{array}{ccc} A& B\\ C& D \end{array} \right],$ 2009年, Tretter^[6]给出了${\cal A}$为主对角占优或次对角占优且相对界为$0$时, 其二次数值域的谱包含性质. 2012年, Muhammad和Marletta^[7]先给出了一类有界分块算子矩阵的二次数值域的近似估计式, 进一步推广到了无界算子情形, 并在2013年给出了Hain-Lüst型算子的二次数值域的范围^[8]. 2017年, Langer和Strauss^[9]利用Schur补和二次数值域研究了主对角占优和次对角占优的无界${\cal J}$-自伴分块算子矩阵, 给出了谱为实数的充分条件, 并导出了非实谱存在的情况下某些实特征值的变分原理. 2018年, Jacob, Tretter, Trunk和Vogt^[10]研究了Hilbert空间中与二阶偏微分方程相关联的分块算子矩阵${\cal A} = \left[\begin{array}{ccc} 0& I\\ -A_{0}& -D \end{array} \right]$, 利用数值域和二次数值域给出了关于算子${\cal A}$的一种新的谱估计方法.

二阶偏微分方程

可转化为抽象的一阶方程

其中$x = (z, \dot{z})^{\top}$, 这样对二阶偏微分方程问题的研究就转化为分析算子${\cal M}$的性质.因此本文我们将研究算子${\cal M}:{\cal D}({\cal M})\subset {\cal D}(A^{\frac{1}{2}})\times H\rightarrow {\cal D}(A^{\frac{1}{2}})\times H,$

其中$H$为Hilbert空间, $A : {\cal D}(A)\subset H\rightarrow H$为一致正的自伴算子, $B : {\cal D}(B)\subset H\rightarrow H$为无界增生线性算子, 即${\rm Re}\langle Bx, x\rangle\ge 0$.对于一致正的自伴算子$A$, 及任意的$\alpha\geq0$, 可定义$H_{\alpha}: = {\cal D}(A^{\alpha})$, 及$\| z \|_{H_{\alpha}} = \| A^{\alpha}z\|_{H}$, 此时$H_{\alpha}$为Hilbert空间; 当$\alpha>0$时, $H$存在完备化空间$H_{-\alpha}: = H_{\alpha}^{*}$, 且伴有范数$\| z \|_{H_{-\alpha}} = \| A^{-\alpha}z\|_{H}$.我们用$\langle \cdot, \cdot\rangle_{H}$或$\langle \cdot, \cdot\rangle$表示空间$H$上的内积, $\langle \cdot, \cdot\rangle_ {H_{-\alpha} \times H_{\alpha}}$表示空间$H_{-\alpha} \times H_{\alpha}$上的一种二元运算.根据Risez表示定理, 任取$x\in H_{\alpha}$, 存在唯一的$x'\in H$, 使得$\langle x', x\rangle_{ H_{-\alpha} \times H_{\alpha}} = \langle x', x\rangle_{H}$, 详见文献[11].特别地, 当$\alpha = 1$时, 有$H_{1}: = {\cal D}(A)$, 对任意的$x\in H_{1}$, 总有一个确定的实数$\| x \|_{H_{1}}$与之对应, 且满足$\| x \|_{H_{1}} = \| Ax\|$; 当$\alpha = \frac{1}{2}$时, 有$H_{\frac{1}{2}}: = {\cal D}(A^{\frac{1}{2}})$, 对于$x\in H_{\frac{1}{2}}$, 有$\| x \| _{H_{\frac{1}{2}}} = \| A^{\frac{1}{2}}x\|$; 当$\alpha = -\frac{1}{2}$时, 存在$H$的一个完备化空间$H_{-\frac{1}{2}}: = H_{\frac{1}{2}}^{*}$, 且任取$x\in H_{-\frac{1}{2}}$, 满足$\| x \|_{H_{-\frac{1}{2}}} = \| A^{-\frac{1}{2}}x\|$.显然, $H_{1}, H_{\frac{1}{2}}$, $H_{-\frac{1}{2}}$均为复数域${\mathbb C}$上的Hilbert空间.此外, 不难验证$A:H_{\frac{1}{2}}\rightarrow H_{-\frac{1}{2}}$与$A^{-1}:H_{-\frac{1}{2}}\rightarrow H_{\frac{1}{2}}$均为有界线性算子.此外, 本文假设$B$为从空间$H_{\frac{1}{2}}$到空间$H_{-\frac{1}{2}}$的有界线性算子且${\cal D}(A)\subset {\cal D}(B)$.

一般来说, 在Hilbert空间中, 并不是所有的无界线性算子都可以表示成分块算子矩阵.对本文中的算子${\cal M}$而言, 它的定义域并不一定能根据空间$H_{\frac{1}{2}}\times H$的分解而进行分解, 因此算子${\cal M}$并不一定是算子矩阵.事实上, 由(1.1)式给定的算子${\cal M}$等于分块算子矩阵${\cal M}|_{H_{1}\times H_{1}}$的闭包, 所以本文利用分块算子矩阵${\cal M}|_{H_{1}\times H_{1}}$的二次数值域来估计算子${\cal M}$的谱的范围.

根据算子${\cal M}$的结构, 结合算子$B$为增生算子, 我们定义以下参数

下面给出本文用到的定义和主要引理.

定义1.1  设${\cal M}$为由(1.1)式给定的算子, 对于$f, g\in H_{1}\times H_{1}\subset{\cal D}({\cal M}), f, g\neq0,$定义

则称集合

为分块算子矩阵${\cal M}|_{H_{1}\times H_{1}}$在空间$H_{\frac{1}{2}}\times H$上的二次数值域.

引理1.1  设$A$为一致正的自伴算子, 则对任意的$x \in {\cal D}(A)$, 有$\| x \|_{H_{\frac{1}{2}}} \geq a \| x \| \geq a^{2}\| x \|_{H_{-\frac{1}{2}}}$, 其中$a = \| A^{-\frac{1}{2}}\|^{-1}$.

证  由$A$为一致正的自伴算子知

进而$\| x \|\geq\| A^{-\frac{1}{2}}\|^{-1} \| x \|_{H_{-\frac{1}{2}}}$, 令$a = \| A^{-\frac{1}{2}}\|^{-1},$则

又

易得

从而有$\| x \|_{H_{\frac{1}{2}}}\geq a \| x \|\geq a^{2}\| x \|_{H_{-\frac{1}{2}}}$.

引理2.1  设${\cal M}$为由(1.1)式给定的算子, 则

(ⅰ) ${\cal M}$为具有有界逆的闭算子且$\overline{{\cal M}|_{ H_{1}\times H_{1}}} = {\cal M}$.

(ⅱ) ${\cal M}$为有界线性算子当且仅当$A$在$H$上有界.

证  (ⅰ)因$A$为一致正自伴算子, 故$0\in\rho (A)$, 即$A^{-1}$存在, 且

由于$A^{-1}:H_{-\frac{1}{2}}\rightarrow H_{\frac{1}{2}}$, $B :H_{\frac{1}{2}}\rightarrow H_{-\frac{1}{2}}$均有界, 则对任意$x\in H_{\frac{1}{2}}$, 存在$M_{1}>0$, $M_{2}>0$使得

即$A^{-1}B$为$H_{\frac{1}{2}}$到$H_{\frac{1}{2}}$的有界线性算子.

任取$x\in H$, 有

即$A^{-1}:H\rightarrow H_{\frac{1}{2}}$有界, 又$I:H_{\frac{1}{2}}\rightarrow H$有界, 所以${\cal M}^{-1}$为$H_{\frac{1}{2}}\times H$到$H_{\frac{1}{2}}\times H$的有界线性算子.

下证${\cal M}$为闭算子.对任意的$(x_{n}, y_{n})^{\top}\subset{\cal D}({\cal M})$, 存在$(x, y)^{\top}\in H_{\frac{1}{2}}\times H_{\frac{1}{2}}$满足

且对于${\cal M}\left[\begin{array}{ccc} x_{n}\\y_{n} \end{array}\right] = \left[\begin{array}{ccc} y_{n}\\-Ax_{n}+By_{n} \end{array}\right]$, 存在$(z, w)^{\top}\in H_{\frac{1}{2}}\times H$满足

由引理1.1及(2.3)式得$\lim \limits _{n \rightarrow \infty} \| y_{n}-z\| = 0$, 又由极限的唯一性及(2.2)式知$y = z$.

又$\lim \limits _{n \rightarrow \infty} a\|-Ax_{n}+By_{n}-w\|_{H_{-\frac{1}{2}}}\leq \lim \limits _{n \rightarrow \infty} \|-Ax_{n}+By_{n}-w\|$, 由(2.4)式得$\lim \limits _{n \rightarrow \infty} \|-Ax_{n}+By_{n}-w\|_{H_{-\frac{1}{2}}} = 0$.进一步, 结合(2.1), (2.3)式与$A, B :H_{\frac{1}{2}}\rightarrow H_{-\frac{1}{2}}$的有界性得$(x, y)^{\top}\in H_{\frac{1}{2}}\times H$且$\lim \limits _{n \rightarrow \infty} \|-Ax+By-w\|_{H_{-\frac{1}{2}}} = 0,$显然$-Ax+By = w$, 故$(x, y)^{\top}\in {\cal D}({\cal M})$且

即${\cal M}$为闭算子.

下证$\overline{{\cal M}|_{ H_{1}\times H_{1}}} = {\cal M}$.因${\cal M}$为闭算子, 且$H_{1}\times H_{1}\subset {\cal D}({\cal M})$, 故$\overline{{\cal M}|_{ H_{1}\times H_{1}}}\subset {\cal M}$, 因此要证$\overline{{\cal M}|_{ H_{1}\times H_{1}}} = {\cal M}$, 只需证${\cal M}\subset\overline{{\cal M}|_{ H_{1}\times H_{1}}}$.

任取$(x, y)^{\top} \in {\cal D}({\cal M})$, 令$f: = -Ax+By\in H$.因$H_{1}$在$H_{\frac{1}{2}}$中稠密, 存在$y_{n}\in H_{1}$, 使得$\lim \limits _{n \rightarrow \infty} \| y_{n}-y\| _{ H_{\frac{1}{2}}} = 0$.再令$x_{n}: = -A^{-1}f+A^{-1}B y_{n}\in H_{1}$, 显然$\lim \limits _{n \rightarrow \infty} \| x_{n}-x\| _{ H_{\frac{1}{2}}} = 0$.由引理1.1得$(x_{n}, y_{n})^{\top}\in H_{1}\times H_{1}$在$H_{\frac{1}{2}}\times H$中收敛且$({\cal M}(x_{n}, y_{n})^{\top})_{n\in{\mathbb N}} = \left(y_{n}, f\right)$在$H_{\frac{1}{2}}\times H$中收敛, 即$(x, y)^{\top}\in {\cal D}(\overline{{\cal M}|_{ H_{1}\times H_{1}}})$, 故${\cal M}\subset\overline{{\cal M}|_{ H_{1}\times H_{1}}}$.

(ⅱ)设${\cal M}$为有界线性算子, 则存在$(x, 0)^{\top}\in {\cal D}({\cal M}), M>0$使得

令$y: = A^{\frac{1}{2}}x$, 则$x = A^{-\frac{1}{2}}y$且(2.5)式化为$\| A^{\frac{1}{2}}y\|\leq M\| y\|$, 即$A^{\frac{1}{2}}$为$H$上的有界线性算子, 于是$A$在$H$上有界.

设$A$在$H$上有界, 存在$x\in H$, 及$N>0$, 使得$\| Ax\|\leq N \| x\|,$即

令$A^{\frac{1}{2}}x = y$, 则$x = A^{-\frac{1}{2}}y$, 将其代入(2.6)式有

由引理1.1知三个范数$\| \cdot\|_{H_{\frac{1}{2}}}, \| \cdot\|_{H_{-\frac{1}{2}}}$, $\| \cdot\|$相互等价, 又${\cal D}(A) = H$, 故$H_{\frac{1}{2}} = H_{-\frac{1}{2}} = H$, 综上所述${\cal M}$为有界线性算子.

性质2.1  设${\cal M}$为由(1.1)式给定的算子, 任取$(f, g)^{\top}\in H_{1}\times H_{1},$$f, g\neq0$, 记

则

引理2.2  设${\cal M}$为由(1.1)式给定的算子, 若$\dim H>1$, 则

其中$W(B)$为$B$的数值域.并且有

证  当$\dim H_{\frac{1}{2}}, \dim H >1$时, 由文献[6, 定理2.4]知$W(B)\cup\{0\}\subset W^{2}({\cal M}|_{H_{1}\times H_{1}})$, 且易得

引理2.2得证.

命题2.1  设${\cal M}$为由(1.1)式给定的算子, 则

证  我们先证明$\sigma_{ap}({\cal M})\subset \overline{W^{2}({\cal M}| _{H_{1}\times H_{1}})}$.由文献[12, 引理2.5.16]知任取$\lambda\in \sigma_{ap}({\cal M}| _{H_{1}\times H_{1}}) = \sigma_{ap}({\cal M})$, 存在$(f_{n}, g_{n})^{\top}\in H_{1}\times H_{1}$满足

可得

不失一般性, 设$b: = \lim \limits _{n \rightarrow \infty}\| f_{n}\| _{ H_{\frac{1}{2}}}, c: = \lim \limits _{n \rightarrow \infty}\| g_{n}\| = 1-b$.若$b = 0$, 则$c = 1-b = 1$与(2.11)式所得的$c = 0$矛盾, 因此$b>0.$

下面考虑

根据(2.11)和(2.12)式可得

代入(2.13)式得

显然$\triangle (\lambda) = 0$, 且$\triangle \not\equiv 0$当且仅当$\lambda\neq z.$根据文献[13, 定理7.2.5]知, 任取$\varepsilon>0$, 存在$N\in {\mathbb N}$, 当$n> N$时, $\bigtriangleup(f_{n}, g_{n};z) = 0$存在零点$z_{n}$使$| z_{n}-\lambda| < \varepsilon.$又因为$z_{n}\in W^{2}({\cal M}| _{H_{1}\times H_{1}}),$所以$\lambda \in \overline{ W^{2}({\cal M}| _{H_{1}\times H_{1}})}$, 即$\sigma_{ap}({\cal M})\subset \overline{W^{2}({\cal M}| _{H_{1}\times H_{1}})}$.再由文献[14, 定理V.3.2]及引理2.1知$\sigma({\cal M})\subset \overline{ W^{2}({\cal M}| _{H_{1}\times H_{1}})}.$

根据命题2.1, 下面我们利用分块算子矩阵${\cal M}|_{H_{1}\times H_{1}}$的二次数值域估计算子${\cal M}$的谱的范围.

定理3.1  设${\cal M}$为由(1.1)式给定的算子, 且存在$k\geq0$使得

则

(ⅰ)若$\xi>0$, 则$\sigma({\cal M})\subset \{\lambda \in {\mathbb C}|\ 0<{\rm Re}\lambda<\frac{\xi}{2}, \ | {\rm Im}\lambda | \leq h_{\xi}({\rm Re}\lambda)\}$, 其中$h_{\xi}(x):[0, \infty)\rightarrow[0, \infty)$且

(ⅱ)若$0<\varphi<\infty$, 则$\sigma({\cal M})\subset \{\lambda \in {\mathbb C}| \ \frac{\varphi}{2}<{\rm Re}\lambda\leq\varphi, \ | {\rm Im}\lambda | \leq h_{\varphi}({\rm Re}\lambda)\}$, 其中$h_{\varphi}(x):[0, \infty)\rightarrow[0, \infty)$且

证  对任意$\lambda\in\sigma({\cal M})\setminus \{0\}\subset W^{2}({\cal M}| _{H_{1}\times H_{1}})\setminus \{0\}$, 由性质2.1知存在$(f, g)^{\top}\in H_{1}\times H_{1},$$\| f\|_{H_{\frac{1}{2}}} = \| g\| = 1$使得

进而得

(ⅰ)由$\xi>0$, 易得${\rm Re}\lambda>0$.当${\rm Im} \lambda\neq 0$时, 由(2.14)与(2.15)式得

等式两边同乘$\frac{{\rm Re}\lambda {\rm Im} \lambda}{{\rm Re}\langle Bg, g\rangle}$得

那么对于$0<{\rm Re}\lambda<\frac{\xi}{2}$, 有${\rm Re}\langle Bg, g\rangle\geq\xi$且

因$h_{\xi}({\rm Re} \lambda) = \frac{k{\rm Re}\lambda}{1-2\frac{{\rm Re}\lambda}{\xi}},$故$| {\rm Im}\lambda |\leq h_{\xi}({\rm Re}\lambda)$, 进而得

当${\rm Im} \lambda = 0$时, 结论显然成立.

(ⅱ)当${\rm Im} \lambda\neq 0$时, 因${\rm Re}\langle Bg, g\rangle\leq\varphi$, 对于$\frac{\varphi}{2}<{\rm Re}\lambda\leq\varphi$, (2.16)式可化为

由$h_{\varphi}({\rm Re}\lambda) = \frac{k{\rm Re} \lambda}{2\frac{{\rm Re} \lambda}{\varphi}-1},$得$| {\rm Im} \lambda |\leq h_{\varphi}({\rm Re}\lambda)$, 故

不难看出, 当${\rm Im} \lambda = 0$时, 结论仍成立.

下面我们对于算子${\cal M}$取具体的参数, 如$\xi = 4, \varphi = 5$, 得到定理3.1中的谱范围如下图.

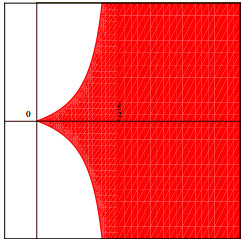
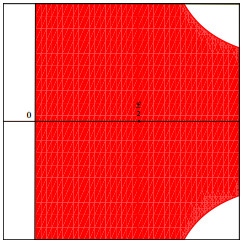
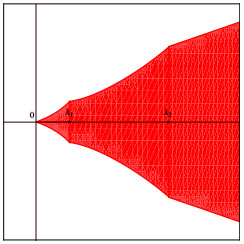
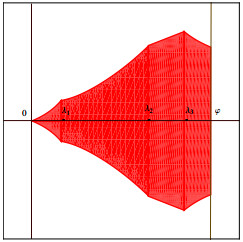
注3.1   图 1和图 2中红色区域为包含二次数值域的区域. 图 1中当${\rm Re} \lambda\in(0, \frac{\xi}{2})$时, 可利用$\xi$对算子${\cal M}$的谱范围进行估计; 当${\rm Re} \lambda\in[\frac{\xi}{2}, \infty)$时, 无法估计谱范围. 图 2中若${\rm Re} \lambda\in(0, \frac{\varphi}{2}]$, 无法估计算子${\cal M}$的谱范围; 当${\rm Re} \lambda\in(\frac{\varphi}{2}, \varphi]$时, 可利用$\varphi$对其谱范围进行估计.

定理3.2  设${\cal M}$为由(1.1)式给定的算子, 存在$k\geq0$使得

若$\delta>0$, 则

其中$h_{\delta}(x)$为函数$\left(x^{2}+y^{2}\right)(y-kx) = \frac{2}{\delta}xy$关于$y$的最大非负解.

证  设$\lambda\in \sigma({\cal M})\setminus \{0\}\subset\overline{ W^{2}({\cal M}| _{H_{1}\times H_{1}})}\backslash\{0\}$, 由性质2.1知存在$(f, g)^{\top}\in H_{1}\times H_{1},$$\| f\|_{H_{\frac{1}{2}}} = \| g\| = 1$使得(2.14), (2.15)式成立.因$\delta>0,$故${\rm Re} \lambda>0$.当${\rm Im}\lambda\neq 0$时, 结合(2.14)和(2.15)式可得

等式两边同乘$\frac{{\rm Re}\lambda {\rm Im} \lambda|\lambda|^{2}}{{\rm Re}\langle Bg, g\rangle}$有

由(1.2)式知$| \langle f, g\rangle_{H_{\frac{1}{2}}}|^{2}\ \ \leq \| g\|_{H_{\frac{1}{2}}}^{2}\leq\frac{{\rm Re} \langle Bg, g\rangle}{\delta},$故有

由$h_{\delta}(x)$为函数$\left(x^{2}+y^{2}\right)(y-kx) = \frac{2}{\delta}xy$的最大非负解, 易得(2.17)式成立当且仅当$|{\rm Im} \lambda|\leq h_{\delta}({\rm Re} \lambda),$因此

易验证, 当${\rm Im} \lambda = 0$时, 结论显然成立.

定理3.1和定理3.2分别给出了算子${\cal M}$关于参数$\xi$, $\delta$的谱估计范围.下面我们将结合利用两个参数$\delta, \xi$研究算子${\cal M}$的谱包含性质.

定理3.3  设${\cal M}$为由(1.1)式给定的算子, 存在$k\geq0$使得

若$\delta>0$, 则

其中$h_{\delta\xi}(x)$为函数$\left(x^{2}+y^{2}\right)^{3}\left(y^{3}-k^{3}x^{3}\right) = \frac{2x^{3}y^{3}}{\delta}\left(\frac{3(x^{2}+y^{2})^{2}}{\xi^{2}}+\frac{1}{\delta^{2}}\right)$关于$y$的最大非负解.

证  任取$\lambda\in\sigma({\cal M})\setminus \{0\}\subset \overline{ W^{2}({\cal M}| _{H_{1}\times H_{1}})}\backslash\{0\}$, 存在$(f, g)^{\top}\in H_{1}\times H_{1},$$\| f\|_{H_{\frac{1}{2}}} = \| g\| = 1$使得(2.14)和(2.15)式成立.由于$\delta>0,$易得${\rm Re} \lambda>0$.当${\rm Im} \lambda\neq 0$时, 结合(2.14)和(2.15)式可得

等式两边同乘$\frac{({\rm Re}\lambda)^{3}({\rm Im} \lambda)^{3}| \lambda|^{6}}{({\rm Re}\langle Bg, g\rangle)^{3}}$有

由于$| \langle f, g\rangle_{H_{\frac{1}{2}}}|^{2}\leq \| g\|_{H_{\frac{1}{2}}}^{2}\leq\frac{{\rm Re}\langle Bg, g\rangle}{\delta}, {\rm Re}\langle Bg, g\rangle\geq\xi,$所以有

记$h_{\delta\xi}(x)$为函数$\left(x^{2}+y^{2}\right)^{3}\left(y^{3}-k^{3}x^{3}\right) = \frac{2x^{3}y^{3}}{\delta}\left(\frac{3\left(x^{2}+y^{2}\right)^{2}}{\xi^{2}}+\frac{1}{\delta^{2}}\right)$的最大非负解, 易得(2.18)式成立当且仅当$|{\rm Im} \lambda|\leq h_{\delta\xi}({\rm Re} \lambda),$故有

当${\rm Im} \lambda = 0$时, 结论显然成立.

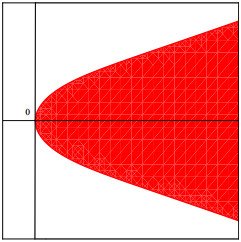
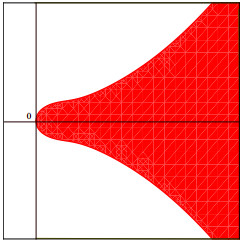
下面我们取具体的参数, 如$\delta = 1.05, \xi = 4$得到定理3.2和定理3.3中的谱范围如下图.

注3.2   图 3和图 4中红色区域为二次数值域的范围, 且分别为算子${\cal M}$关于参数$\delta$及结合两个参数$\delta$与$\xi$时的谱估计范围.

定理3.1, 定理3.2, 定理3.3分别利用参数$\varphi$, $\xi$, $\delta$, 以及结合两个参数$\delta, \xi$给出了算子${\cal M}$谱的范围, 下面我们为了分析定理3.1, 定理3.2, 定理3.3中谱估计之间的关系, 作如下的数值分析.

若$\delta>0$, 则$\xi>0$, 所以当定理3.2成立时, 定理3.1$({\rm i})$, 定理3.3均成立.对于以上参数值$\delta = 1.05, \xi = 4$, 计算得$h_{\xi}(x)$与$h_{\delta\xi}(x)$交点的实部为$\lambda_{1}: = 0.82$, $h_{\delta\xi}(x)$与$h_{\delta}(x)$交点的实部为$\lambda_{2}: = 3.25$, 且当$0<x<\lambda_{1}$时, $h_{\xi}(x)\leq h_{\delta\xi}(x)$; 当$\lambda_{1}\leq x\leq\lambda_{2}$时, $h_{\delta\xi}(x)\leq\min\{h_{\xi}(x), h_{\delta}(x)\}$; 当$x>\lambda_{2}$时, $h_{\delta}(x)\leq h_{\delta\xi}(x)$.如图 5, 任取${\rm Re}\lambda\in(0, \lambda_{1})$, 有$|{\rm Im}\lambda|\leq h_{\xi}({\rm Re}\lambda)$, 显然定理3.1 (i)的估计最为精确; 对于${\rm Re}\lambda\in[\lambda_{1}, \lambda_{2}]$, 有$|{\rm Im}\lambda|\leq h_{\delta\xi}({\rm Re}\lambda)$, 此时定理3.3的估计较为精确; 设${\rm Re}\lambda\in(\lambda_{2}, \infty)$, 有$|{\rm Im}\lambda|\leq h_{\delta}({\rm Re}\lambda)$, 即定理3.2的估计更为精确, 故有

在此基础上, 若$\varphi$有界, 不妨取$\varphi = 5$, 此时${\cal M}$为有界算子且计算得$h_{\delta}(x)$与$h_{\varphi}(x)$交点的实部为$\lambda_{3}: = 4.26$, 且当$\lambda_{3}\leq x\leq\varphi$时, $h_{\varphi}(x)\leq h_{\delta}(x)$.如图 6, 对任意${\rm Re}\lambda\in[\lambda_{3}, \varphi]$, 有$|{\rm Im}\lambda|\leq h_{\varphi}({\rm Re}\lambda)$, 此时定理3.1 (ⅱ)的估计较为精确, 故有

于是对于有界算子${\cal M}$得到了更为精细的谱包含关系.