1 引言
以往的研究工作大都侧重于从流动的稳定性和分岔理论开展研究,主要是利用分岔理论来解释和分析实验中观察到的流动发展到湍流前的各种涡流及其相互演化的过程,以及从层流过渡到湍流的方式及仿真等,而对截断模型的物理背景、物理意义以及流动的生成机理和能量演化等问题很少有文献涉及,诸如能量的守恒,内能,耗散和外力等相互转化和物理意义等问题几乎无人关注.因此探讨复杂流动模式和混沌的生成机理及其物理意义等相关问题是非常有意义和具有挑战性的.本文把五模类Lorenz系统的状态变量视为角动量,将矢量场分解为惯性力矩,耗散力矩和外力矩,不同的力矩的耦合视为不同的动力模式,通过分析各种力矩耦合模态和混沌生成的因果关系,揭示五模类Lorenz系统动力学和能量特征以及混沌生成的力学机理.
混沌系统按其各项及相互作用是相当复杂的.如果从力学角度对混沌进行研究,可以从中发现更多的混沌基本成因.从力学角度研究混沌系统已经有了良好的开端,阿诺德用Kolmogorov系统来描述具有哈密顿函数的不同的强迫动力系统,流体动力系统等[13]. Pasini和Pelino对Lorenz系统进行了研究,并给出了统一的柯尔莫哥洛夫(Kolmogorov)和洛伦茨(Lorenz)系统[14-16].齐和梁将混沌系统转换成Kolmogorov形系统,进行力的分析,解释角动量的混沌状态,讨论能量循环[17-19].借助扩展的Kolmogorov系统, Pelino等研究了洛伦兹系统的能量转换[20].文献[16]研究了Chen混沌系统力学机理与能量转换,将Chen混沌系统转换成Kolmogorov形系统,通过不同力矩的结合分析和研究了Chen混沌系统产生混沌的关键因素和物理意义.研究了哈密顿能量,动能和势能之间的相互转换.讨论了能量与雷诺数之间的关系.文献[17]研究了齐四翼混沌系统的力学机理与能量转换,通过与Kolmogorov系统和欧拉方程的比较,把四翼混沌系统的矢量场分解为惯性力矩、内力矩、耗散和外力矩来探讨产生混沌的基本因素.利用Lie-Poisson括号揭示哈密顿能,动能与势能的相互转换.通过五种情形分析研究了四翼混沌吸引子不同类型力矩的功能和作用以及产生不同类型动力学模式的关键因素.此外,借助扩展的Kolmogorov系统, Pelino等研究了洛伦兹系统的能量转换[18].基于这些工作本文研究了五模类Lorenz系统力学机理、物理意义和能量演化.并估计了混沌吸引子的界.
由于五模系统的全局吸引子是非常复杂和难于计算的.系统的轨道从一个不稳定的平衡点移动到另一个不稳定的平衡点,相应地,轨道和平衡点之间的距离随参数和时间的不同而变化.我们发现,卡西米尔(Casimir)函数与距离有密切关系,关于洛伦茨吸引子的可预测性和能量可以通过能量转换来进行研究[20].因此,通过引入卡西米尔函数的导数,我们给出了五模系统的能量演化,并且分析了它们的动力学和能量演化.
本文的结构如下:第2节将五模系统转换为Kolmogorov系统.第3节分析了不同动力模式的力学机理.在第4节,引入卡西米尔函数来获得混沌吸引子的边界,探讨它的动态行为.第5节按扩展Kolmogorov系统和能量转换,分析了五模系统的力学机制,能量转换和卡西米尔函数的关系.最后,第6部分是总结.
2 五模类Lorenz系统及其Kolmogorov系统
Lorenz方程源于满足一定的边界条件的Navier-Stokes方程的适当截断,通常的程序是在方程的展开式中截取有限项. Boldrighini和Franceschini考虑平面不可压缩Navier-Stokes方程,得到了下列五模方程组
这里
为了发现系统(2.1)的状态变量的物理意义和系统(2.1)的力学机理我们引进如下的Kolmogorov系统
其中
其中
注1 变量
3 系统(2.5)的动力学机制及其分析
本节我们研究不同类型的力矩对系统(2.5)的影响,从而发现产生混沌的关键因素.
情形1 系统只包含惯性力矩(由动能
Hamiltonian(动能)函数的导数
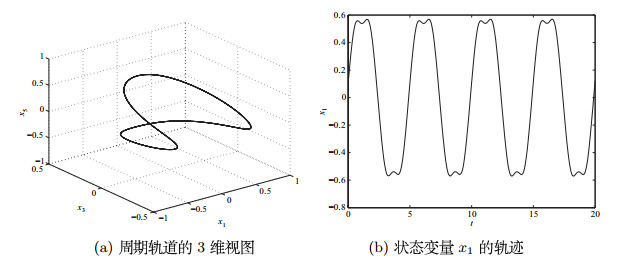
图 1
图 2
情形2 系统包含哈密顿函数中的惯性力矩(由动能
容易获得
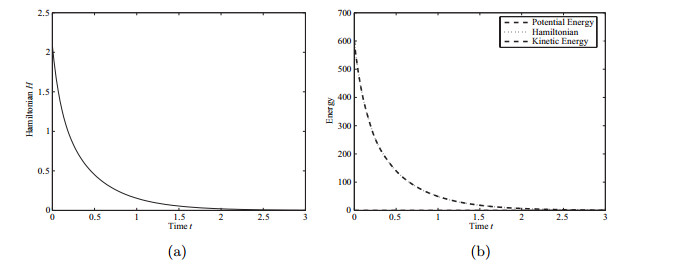
其中V是系统相空间的体积.因此,此情形下系统是耗散的,即相空间的体积在流量下以指数形式收缩[22].哈密顿函数的变化率是
图 3
情形3 系统在惯性力矩和外力矩下,即系统包含内能和驱动因素,但不包含耗散因素,相应的方程为
由于有了外力矩
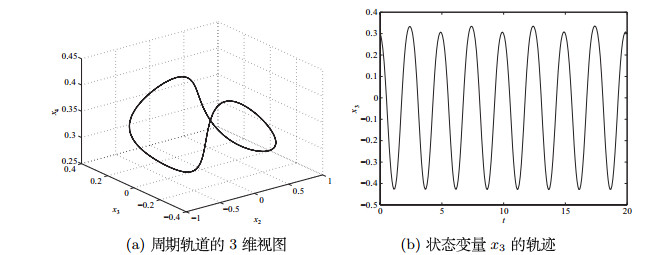
图 4
图 5
为了分析和比较各种力矩对五模系统动力学所起的作用,我们讨论了上面虚拟的三种情形,下面的情形4才具有真实的物理意义.
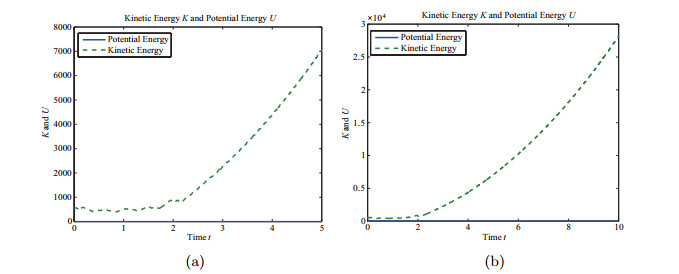
情形4 系统在全部力矩下,即系统包含内能,同时包含耗散因素和驱动因素,相应的方程为,
当
图 6
图 7
4 系统(2.5)的卡西米尔(Casimir)函数及其全局稳定性分析
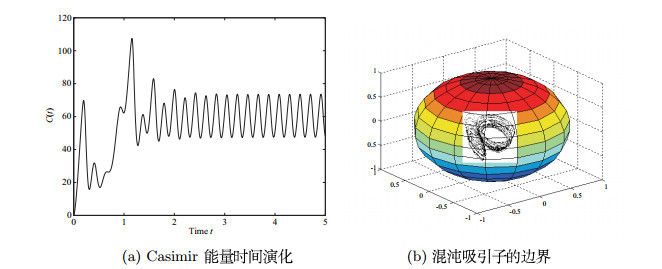
混沌系统具有一些奇异的性质:如初始灵敏性和解的有界性.对于非混沌系统,正Lyapunov指数意味着系统解无限制地增长.然而,对于一个有界的混沌吸引子来说,其轨线增长的同时在不断的折叠,因此,解的边界性质在混沌系统研究中是至关重要的.通常很难找到混沌吸引子的边界,利用拉格朗日乘数法和卡西米尔函数法,我们得到了五模系统混沌吸引子的边界.数值模拟表明,这是一个清晰的边界.卡西米尔函数
这意味着在Lie-Poisson括号下卡西米尔函数与每个函数交换[21].对于五模系统来说,卡西米尔函数定义为
从方程(2.4)和文献[21],我们有
其中
令
显然
定理4.1 卡西米尔函数被限制在如下集合内
证 根据上述分析,
定义拉格朗日函数
通过计算我们得到如下关于变量的导数
因此得到两个解
所以,
证毕.
图 8
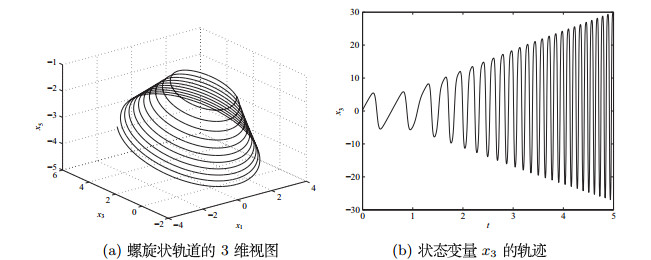
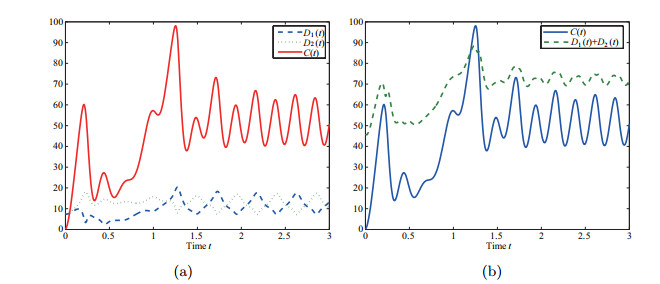
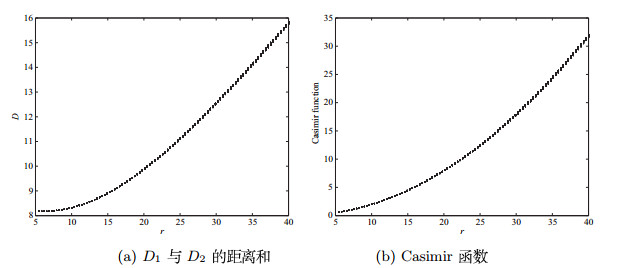
为了显示卡西米尔函数与平衡点
这表示系统(2.5)的轨道与平衡点
图 9
图 10
图 11
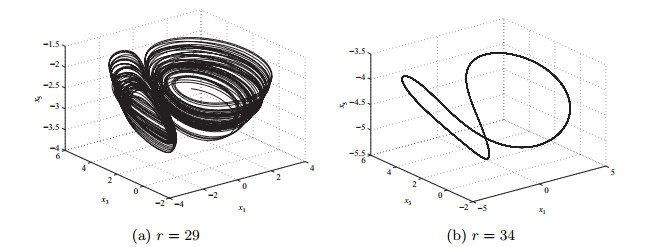
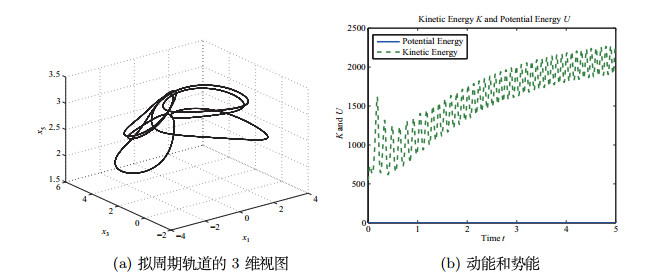
根据以上理论分析和仿真结果,我们得出如下结论,当
表 1
0 | |||||
| 定点 | 稳定结点 | 鞍结点(一个方向不稳,另两个方向稳定) | |||
| 定点 | 不存在 | 稳定结点 | 稳定焦点 | 稳定焦点 | 鞍点 |
| 系统(2.1)相空间中的运动情况 | 趋于稳定定态 | 趋于稳定定态 | 运动最终按螺旋线趋于 | 同左,但越靠近 | 不稳定极限环(亚临界霍普夫分岔) |
| 动能 | 最小值 | 逐渐增大 | 保持增大 | 增长 | |
| Casimir函数 | 最小值 | 逐渐增大 | 保持增大 | 增长 | |
| 不存在 | 逐渐递增 | 递增增大 | 逐渐 | ||
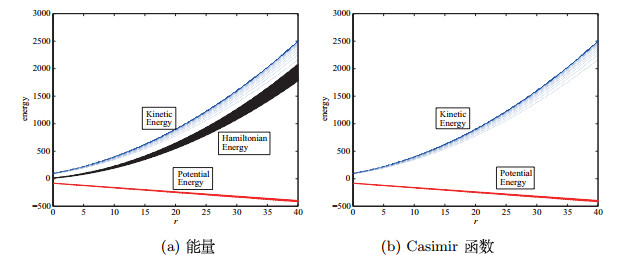
5 能量转换
其中
其中
根据方程(2.3)和(5.2),我们有
那么
因此,动能的变化率与势能、耗散能、外能量有一定的关系.
由于
然后,五模系统的能量转换可以写成
这考虑了在
五模系统有螺旋式轨道,它的轨道从一个不稳定的平衡点移动到另一个不稳定的平衡点.当轨道远离不稳定的平衡点之一时,
虽然五模系统与Lorenz系统不同,但能量转换时间演化与文献[18]的结果相似,能量、西米尔函数以及
6 结论
本文研究了五模类洛伦兹系统的动力学机理和能量转换,通过理论和数值结果揭示了五模系统的力学机制和物理意义.首先,探讨了五模类洛伦兹系统作为柯尔莫哥洛夫系统的力学和物理意义.剖析了五模混沌系统三种不同类型的力矩,研究了这些力矩的耦合的四种情况,探讨了产生混沌的关键因素.在保守的情况下,哈密顿量是一个常数,相应的方程产生周期解.当耗散力矩或外力矩加入到保守系统中时,哈密顿函数趋近于零或无穷大,对应的系统不会产生混沌.当考虑到所有力矩时,五模系统才产生混沌.对于五模系统,内能、耗散因素和驱动因素并存是产生混沌的必要条件,而且,只有当耗散与驱动相匹配时,系统才能生成混沌.增加的动能导致流动不稳定,通过分岔最终到达混沌.其次,本文将五模混沌系统作为一个扩展的Kolmogorov系统研究了其力学和物理意义.引进卡西米尔函数来分析系统动力学和能量转换.两种不稳定平衡点的距离之和与卡西米尔函数有密切的关系,它们的时间演化是一致的.卡西米尔函数是内能,因此,它的变化速率是耗散与供给能量(外力矩)之间的交换速率.内能的导数起着能量转换的作用,平衡点距离的时间演化也有类似的动态.
五模系统是耗散系统,其有界性是不平凡的,通过拉格朗日乘数法和卡西密尔函数法,得到了混沌吸引子的一个清晰的边界,数值仿真显示了方法的有效性.
参考文献
Deterministic nonperiodic flow
DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [本文引用: 1]
Numerical and physical modeling of the dynamics of the lorenz system
A five-dimensional truncation of the plane incompressible Navier-Stokes equations
DOI:10.1007/BF01197511 [本文引用: 1]
A seven-modes truncation of the plane incompressible Navier-Stokes equations
A five-mode truncation of the Navier-Stokes equations on a three-dimensional torus
Lyapunov dimension formula for the global attractor of the Lorenz system
DOI:10.1016/j.cnsns.2016.04.032
On differences and similarities in the analysis of Lorenz, Chen, and Lu systems
Three-dimensional Navier-Stokes equations trancated on a torus
Breaking and disappearance of tori
DOI:10.1007/BF01224828 [本文引用: 1]
Torsion and attractors in the Kolmogorov hydrodynamical system
DOI:10.1016/S0375-9601(98)00113-3 [本文引用: 1]
A unified view of Kolmogorov and Lorenz systems
DOI:10.1016/S0375-9601(00)00620-4 [本文引用: 1]
Dissipation in Lie-Poisson systems and the Lorenz-84 model
DOI:10.1016/S0375-9601(01)00764-2 [本文引用: 2]
Mechanical analysis and energy conversion of Chen chaotic system
Mechanical analysis of Chen chaotic system
DOI:10.1016/j.chaos.2017.03.021 [本文引用: 2]
Mechanical analysis of Qi four-wing chaotic system
DOI:10.1007/s11071-016-2949-0 [本文引用: 2]
Energy cycle for the Lorenz attractor
DOI:10.1016/j.chaos.2013.09.005 [本文引用: 3]
Thoughts on brackets and dissipation:old and new