平面不可压缩Navier-Stokes方程五模系统的力学机理及能量演化

摘要/Abstract

摘要：

该文研究了平面不可压缩Navier-Stokes方程五模系统的力学机理及能量演化问题，通过将五模混沌系统转换成Kolmogorov形系统，把系统的力矩分为三种类型：惯性力矩，耗散力矩和外力矩.通过不同力矩的结合分析和研究了系统产生混沌的关键因素和物理意义.讨论了能量与雷诺数之间的关系.研究表明三种力矩的耦合是产生混沌的必要条件，而且只有耗散力矩和驱动力矩（外力矩）相匹配时，系统才能产生混沌，其中任何两种力矩耦合均不可能产生混沌.外力矩给系统提供能量，导致系统失稳出现分岔与混沌.引进Casimir函数分析系统的动力学行为和能量演化，并估计混沌吸引子的界.Casimir函数反映了能量转换和轨道与平衡点间的距离.

关键词: 力学机理, 能量演化, Kolmogorov系统, 混沌

Abstract:

In this paper we study dynamical mechanism and energy evolution of a five-modes system of the Navier-Stokes equations for a two-dimensional incompressible fluid on a torus. The five-modes system is transformed into Kolmogorov type system, which is decomposed into three types of torques:inertial torque, dissipation and external torque. Combining different torques, key factors of chaos generation and the physical meaning of the five-modes system are studied. The evolution of energy is investigated, the relationship between the energies and the Reynolds number is discussed. We conclude that the combination of the three torques is necessary conditions to produce chaos, and only when the dissipative torques match the driving torques (external torque) the system can produce chaos. While any combination of two types of torques cannot produce chaos. The external torque supply the energy for the system, and that leads to bifurcation and chaos. The Casimir function is introduced to analyze the system dynamics, and its derivation is chosen to formulate energy evolution. The bound of chaotic attractor is obtained by the Casimir function and Lagrange multiplier. We find that the Casimir function reflects the energy evolution and the distance between the orbit and the equilibria.

Key words: Dynamical Mechanism, Kolmogorov system, Chaos

中图分类号:

O175.1

王贺元. 平面不可压缩Navier-Stokes方程五模系统的力学机理及能量演化[J]. 数学物理学报, 2020, 40(2): 315-327.

Heyuan Wang. Dynamical Mechanism and Energy Evolution of a Five-Modes System of the Navier-Stokes Equations For a Two-Dimensional Incompressible Fluid on a Torus[J]. Acta mathematica scientia,Series A, 2020, 40(2): 315-327.

图/表 12

图 1

图 2

图 3

图 4

图 5

图 6

图 7

图 8

图 9

图 10

图 11

表 1

参考文献 24

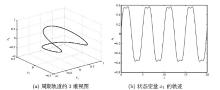
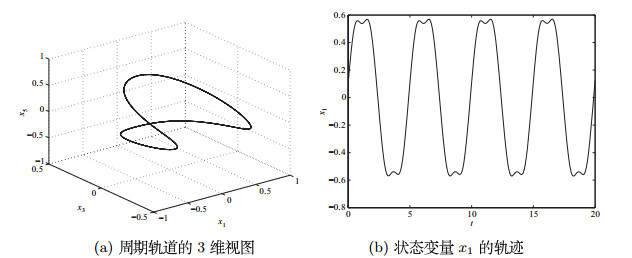
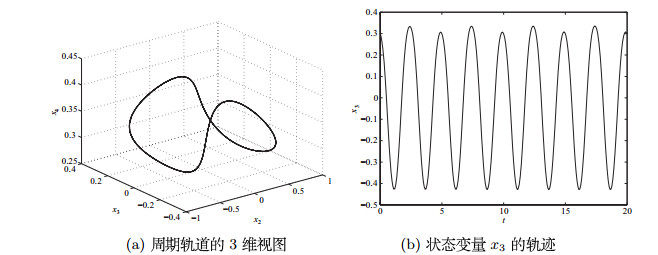
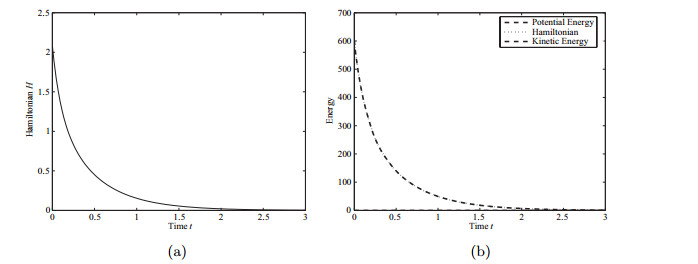
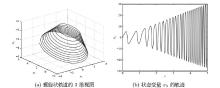
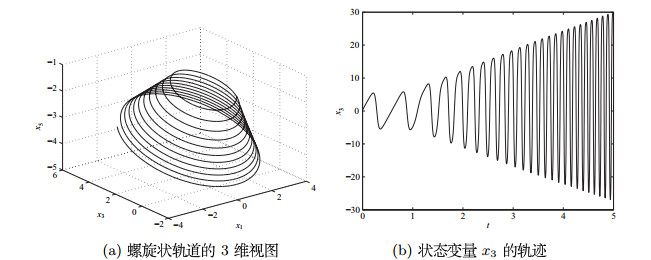
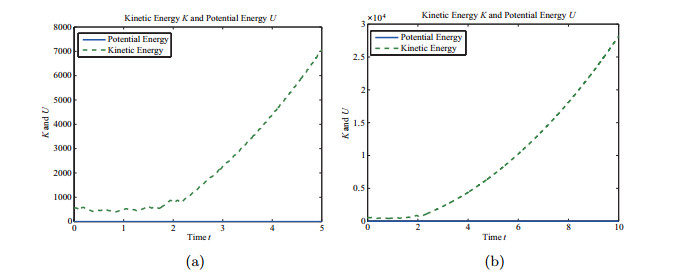
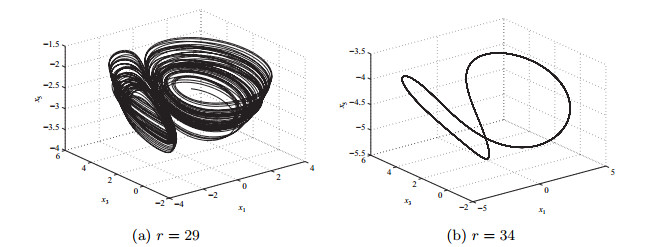
1	Lorenz N E . Deterministic nonperiodic flow. Journal of the Atmospheric Sciences, 1963, 20, 130- 141 doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
2	Teman R. Infinite Dimensional Dynamic System in Mechanics and Physics. New York: Springer-Verlog, 2000
3	Pchelintsev A N . Numerical and physical modeling of the dynamics of the lorenz system. Numerical Analysis and Applications, 2014, 7 (2): 159- 167 doi: 10.1134/S1995423914020098
4	Boldrighini C , Franceschini V . A five-dimensional truncation of the plane incompressible Navier-Stokes equations. Communications in Mathematical Physics, 1979, 64, 159- 170 doi: 10.1007/BF01197511
5	Sparrow C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors. New York: Springer Verlag, 1982
6	Franceschini V , Tebaldi C . A seven-modes truncation of the plane incompressible Navier-Stokes equations. Journal of Statistical Physics, 1981, 25 (3): 397- 417
7	Hilborn R C . Chaos and Nonlinear Dynamics. Landon: Oxford Univ Press, 1994
8	Franceschini V , Inglese G , Tebaldi C . A five-mode truncation of the Navier-Stokes equations on a three-dimensional torus. Commun Mech Phys, 1988, 64, 35- 40
9	Leonov G A , Kuznetsov N V , Korzhemanova N A , Kusakin D V . Lyapunov dimension formula for the global attractor of the Lorenz system. Communications in Nonlinear Science and Numerical Simulation, 2016, 41, 84- 103 doi: 10.1016/j.cnsns.2016.04.032
10	Leonov G A , Kuznetsov N V . On differences and similarities in the analysis of Lorenz, Chen, and Lu systems. Applied Mathematics and Computation, 2015, 256, 334- 343 doi: 10.1016/j.amc.2014.12.132
11	Franceschini V , Zanasi R . Three-dimensional Navier-Stokes equations trancated on a torus. Nonlinearity, 1992, 4, 189- 209
12	Franceschini V , Tebaldi C . Breaking and disappearance of tori. Commun Math Phys, 1984, 94, 317- 329 doi: 10.1007/BF01224828
13	Arnold V . Kolmogorov's hydrodynamic attractors. Proc R Soc Lond A, 1991, 434 (19): 19- 22
14	Pasini A , Pelino V , Potesta S . Torsion and attractors in the Kolmogorov hydrodynamical system. Phys Lett A, 1998, 241, 77- 83 doi: 10.1016/S0375-9601(98)00113-3
15	Pasini A , Pelino V . A unified view of Kolmogorov and Lorenz systems. Phys Lett A, 2000, 275, 435- 446 doi: 10.1016/S0375-9601(00)00620-4
16	Pelino V , Pasini A . Dissipation in Lie-Poisson systems and the Lorenz-84 model. Phys Lett A, 2001, 291, 389- 396 doi: 10.1016/S0375-9601(01)00764-2
17	Liang X Y , Qi G Y . Mechanical analysis and energy conversion of Chen chaotic system. General and Applied Physics, 2017, 47 (4): 288- 294
18	Liang X Y , Qi G Y . Mechanical analysis of Chen chaotic system. Chaos, Solitons and Fractals, 2017, 98, 173- 177 doi: 10.1016/j.chaos.2017.03.021
19	Qi G , Liang X . Mechanical analysis of Qi four-wing chaotic system. Nonlinear Dyn, 2016, 86 (2): 1095- 1106 doi: 10.1007/s11071-016-2949-0
20	Pelino V , Maimone F , Pasini A . Energy cycle for the Lorenz attractor. Chaos Soliton Fract, 2014, 64, 67- 77 doi: 10.1016/j.chaos.2013.09.005
21	Marsden J, Ratiu T. Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems. Berlin: Springer, 2002
22	Strogatz S H. Nonlinear Dynamics and Chaos. Reading, MA: Addison-Wesley, 1994
23	Morrison P J . Thoughts on brackets and dissipation:old and new. Journal of Physics:Conference Series, 2009, 169 (1): 012006
24	Doering C R , Gibbon J D . On the shape and dimension of the Lorenz attractor. Dyn Stab Syst, 1995, 10 (3): 255

$r$ -值范围	$0 < r < r_1$ 0 $r_1=5\sqrt{3/2}$	$r>r_1$ $r_e=28.71\quad r_g=28.72\quad r_h=28.73$
定点$O$	稳定结点	鞍结点(一个方向不稳,另两个方向稳定)
定点$P^{+}$和$P^{-}$	不存在	稳定结点	稳定焦点	稳定焦点	鞍点
系统(2.1)相空间中的运动情况	趋于稳定定态$O$	趋于稳定定态$P^{+}$或$P^{-}$	运动最终按螺旋线趋于$P^{+}$或$P^{-}$	同左,但越靠近$r_h$,轨线在$P^{+}$和$P^{-}$之间来回跳动的越频繁,出现暂态混沌,最终趋于$P^{+}$或$P^{-}$	不稳定极限环(亚临界霍普夫分岔)
动能	最小值	逐渐增大		保持增大	增长
Casimir函数	最小值	逐渐增大		保持增大	增长
$D_1$与$D_2$之和	不存在	逐渐递增		递增增大	逐渐

[1]	王贺元. Couette-Taylor流的力学机理与能量转换[J]. 数学物理学报, 2020, 40(1): 243-256.
[2]	王志,闫理坦,余显烨. 分数噪声驱动的随机热方程解的局部时[J]. 数学物理学报, 2019, 39(3): 582-595.
[3]	黄燮桢,刘永建,黄秋健. 一类新混沌系统的几何分析[J]. 数学物理学报, 2019, 39(2): 339-347.
[4]	王建军. ∑(X)上权移位算子的不变分布混沌性[J]. 数学物理学报, 2018, 38(3): 446-453.
[5]	姚玉武, 陈秀, 牛欣. 复扇形指标集上的分布混沌[J]. 数学物理学报, 2017, 37(5): 950-961.
[6]	吴新星. 关于弱Specification性质的一个注记[J]. 数学物理学报, 2017, 37(4): 601-606.
[7]	杨纪华, 张二丽, 刘媚. 具时滞反馈金融系统的动力学分析与混沌控制[J]. 数学物理学报, 2017, 37(4): 767-782.
[8]	王贺元, 崔进. 旋转流动混沌行为的全局稳定性分析及数值仿真[J]. 数学物理学报, 2017, 37(4): 783-792.
[9]	王贺元. 平面不可压缩磁流体动力学五模类Lorenz方程组的动力学行为及其数值仿真[J]. 数学物理学报, 2017, 37(1): 199-216.
[10]	吴新星, 王建军. 关于P-极小动力系统的一些注记[J]. 数学物理学报, 2016, 36(5): 879-885.
[11]	卢天秀, 朱培勇, 吴新星. 非自治离散系统的分布混沌性[J]. 数学物理学报, 2015, 35(3): 558-566.
[12]	袁大琏, 吕杰. 可数度量空间上的完全分布混沌映射[J]. 数学物理学报, 2011, 31(2): 298-304.
[13]	王立冬;楚振艳;廖公夫. ∑上的非弱几乎周期的回复点集和SS混沌集[J]. 数学物理学报, 2006, 26(5): 778-784.
[14]	胡汉平, 刘双红, 王祖喜, 吴晓刚. 一种混沌多相伪随机序列[J]. 数学物理学报, 2004, 24(2): 251-256.
[15]	丁义明, 范文涛. 一簇Lorenz映射的混沌行为与统计稳定性[J]. 数学物理学报, 2001, 21(4): 559-569.