分数阶微分方程产生于一些反常扩散模型,有着深入的物理背景和丰富的理论意义^[1].其特点在于它反映的不仅是局部或某个点的性质或数量,还考虑了历史以及非局部分布式的影响.与此同时分数阶微分算子在建立物质的力学和电学性能模型方面也有非常好的优势,具有参数物理意义清楚、描述准确等特点,已成为一个描述各种复杂力学行为的重要工具^[2-4].由于分数阶微分方程的解析解大多很难显式给出,因此研究解决分数阶微分方程的数值解法是必要的^[5-7].

近些年对于各类分数阶扩散方程的数值解法,已有不少的研究成果. Tadjeran等^[8]研究了在时间和空间上具有二阶精度的数值方法来解决一类变系数初边值分数阶扩散方程,其精度估计采用了经典Crank-Nicholson(C-N)方法与空间外推法的结合. Zhao^[9]等利用Caputo分数阶导数对一系列二维多项时间分数阶扩散方程构造了完全离散格式,通过插值处理技术给出其超收敛于时间$2-\alpha$阶,空间二阶. Chen^[10]等人根据对分数阶导数的不同定义,利用傅里叶方法证明了显式及隐式格式的稳定性,同时结合外推技术构造了一类高精度算法. Gao和Sun^[11]对分数阶扩散方程构造了一类紧致差分格式,用能量法证明了格式无条件稳定的同时在时间$2-\alpha$阶,空间四阶收敛.

时间分数阶慢扩散方程是将经典扩散方程的一阶时间导数项用时间分数阶导数项$\alpha$ ($0 < \alpha < 1$)替换而成,该方程在自然科学和工程应用方面运用较广. Liu等^[12]对时间分数阶扩散方程提出了一个离散的非马尔科夫随机游走近似分析,在空间和时间上都采用一阶离散的方式,得到了一些稳定性条件.一类无条件稳定和收敛的时间分数阶扩散方程的隐式差分方法被Shen等提出,其在时间上$2-\alpha$阶、空间上二阶收敛^[13]. Yuste等^[14-15]对时间分数阶慢扩散问题用Grunwald-Letnikov(G-L)逼近的方法构建了向前Euler差分格式及加权平均有限差分方法并证明了稳定性. Xu等^[16]将Galerkin谱方法和Legendre配点法直接运用在时间分数阶导数的求解中,通过多项式函数组合来逼近原方程的解,在时间维上得到了$2-\alpha$阶的误差估计.

本文根据传统差分方法给出了求解时间分数阶慢扩散方程的显-隐格式和隐-显格式,该格式在保证良好精度的前提下加快了计算速度.理论证明了该类格式是无条件稳定的,通过数值试验验证了理论分析,表明格式对于解决时间分数阶慢扩散方程是有效的.

考虑如下时间分数阶慢扩散方程

(2.1) $ \begin{equation}\label{1} \frac{\partial^\alpha u(x, t)}{\partial t^\alpha}=\frac{\partial^2 u(x, t)}{\partial x^2}, \;\; x\in[0, L], t\in[0, T], \alpha\in(0, 1) , \end{equation} $

(2.2) $\begin{equation}\label{2} u(0, t)=u(L, t)=0, \;\;u(x, 0)=f(x), \end{equation} $

$u(x, t)$表示在t时刻x点处的扩散浓度值, $\frac{\partial^\alpha u(x, t)}{\partial t^\alpha}$以Caputo分数阶导数定义为

(2.3) $ \begin{equation}\label{3} \frac{\partial^\alpha u(x, t)}{\partial t^\alpha}=\frac{1}{\Gamma(1-\alpha)}\int_0^t\ \frac{\partial u(x, \xi)}{\partial \xi}\frac{1}{(t-\xi)^\alpha}{\rm d}\xi, \;\; 0<\alpha<1 .\end{equation} $

通过有限的正弦变换和拉普拉斯变换,可求得在边界条件(2.2)下方程(2.1)的解析解

(2.4) $\begin{equation}\label{4} u(x, t)=\frac{2}{L}\sum\limits_{n=1}^{\infty}E_\alpha(-a^2n^2t^\alpha)\sin(anx)\int_0^t\ f(r)\sin(anr){\rm d}r , \end{equation} $

其中$E_\alpha$是Mittag-Leffler函数^[5], $E_\alpha(z)=\sum\limits_{k=0}^{\infty}\frac{z^k}{\Gamma(\alpha k+1)}, a=\frac{\pi}{L}$,同时给出一些特殊的Mittag-Leffler类型函数

(2.5) $\begin{equation}\label{5} E_{\alpha, \beta}(z)=\sum\limits_{k=0}^{\infty}\frac{z^k}{\Gamma(\alpha k+\beta)}, \;\;E_{1, 1}(z)=\sum\limits_{k=0}^{\infty}\frac{z^k}{\Gamma(k+1)}=\sum\limits_{k=0}^{\infty}\frac{z^k}{k!}=\exp(z) , \end{equation}$

(2.6) $ \begin{equation}\label{6} E_{1}(-z)=\exp(-z), \;\;E_{\frac{1}{2}}(z)=\sum\limits_{k=0}^{\infty}\frac{z^k}{\Gamma(\frac{k}{2}+1)}=\exp(z^2)erfc(-z) , \end{equation} $

其中$erfc(z)$为误差函数, $erfc(z)=\frac{2}{\sqrt\pi}\int_z^\infty\exp(-t^2){\rm d}t$.

现对该模型进行显-隐差分格式的构造.定义$t_k=k\tau, k=0, 1, \cdots n; x_i=ih, $$i=0, 1, $$\cdots, m$.时间步长$\tau=\frac{T}{n}$,空间步长$h=\frac{L}{m}$,令$u_i^k$为$u(x_i, t_k)$的数值逼近,则时间分数阶导数可展开为如下形式

$ \begin{eqnarray*} \frac{\partial^\alpha u(x_i, t_k)}{\partial t^\alpha} &=& \frac{1}{\Gamma(1-\alpha)}\sum\limits_{j=0}^{k}\int_{j\tau}^{(j+1)\tau}\frac{\partial u(x, \xi)}{\partial\xi}\frac{1}{(t_{k+1}-\xi)^\alpha}{\rm d}\xi \\ &\approx& \frac{1}{\Gamma(1-\alpha)}\sum\limits_{j=0}^{k}\frac{u(x_i, t_{j+1})-u(x_i, t_j)}{\tau}\int_{j\tau}^{(j+1)\tau}\frac{{\rm d}\xi}{(t_{k+1}-\xi)^\alpha}\\ &=& \frac{1}{\Gamma(1-\alpha)}\sum\limits_{j=0}^{k}\frac{u(x_i, t_{j+1})-u(x_i, t_j)}{\tau}\int_{(k-j)\tau}^{(k-j+1)\tau}\frac{{\rm d}\eta}{\eta^\alpha}\\ &=& \frac{1}{\Gamma(1-\alpha)}\sum\limits_{j=0}^{k}\frac{u(x_i, t_{k+1-j})-u(x_i, t_{k-j})}{\tau}\int_{j\tau}^{(j+1)\tau}\frac{{\rm d}\eta}{\eta^\alpha}\\ &=& \frac{\tau^{1-\alpha}}{\Gamma(2-\alpha)}\sum\limits_{j=0}^{k}\frac{u(x_i, t_{k+1-j})-u(x_i, t_{k-j})}{\tau}[(j+1)^{1-\alpha}-j^{1-\alpha}].\end{eqnarray*}$

令$b_j=(j+1)^{1-\alpha}-j^{1-\alpha}$, $j=0, 1, \cdots $,定义以上近似形式为

$ \begin{eqnarray*} L_{h, \tau}^\alpha u(x_i, t_{k+1})=\frac{\tau^{-\alpha}}{\Gamma(2-\alpha)}\sum\limits_{j=0}^{k}b_j[u(x_i, t_{k+1-j})-u(x_i, t_{k-j})]\end{eqnarray*} $

为构造方程(2.1)的显-隐格式,首先给出两种离散格式

(1)古典隐式格式

(2.7) $\begin{equation}\label{7} L_{h, \tau}^\alpha u(x_i, t_{k+1})=\frac{1}{h^2}(u_{i+1}^{k+1}-2u_i^{k+1}+u_{i-1}^{k+1}) ;\end{equation} $

(2)古典显式格式

(2.8) $\begin{equation}\label{8} L_{h, \tau}^\alpha u(x_i, t_{k+1})=\frac{1}{h^2}(u_{i+1}^{k}-2u_i^{k}+u_{i-1}^{k}) .\end{equation} $

令$\mu=\frac{\tau^\alpha}{h^2}$, $r=\mu\Gamma(2-\alpha)$,上述格式可以写成如下形式

当$k=0$时

(2.9) $ \begin{equation}\label{9} -ru_{i+1}^{1}+(1+2r)u_i^1-ru_{i-1}^1=u_i^0, u_i^1=ru_{i+1}^0+(1-2r)u_i^0+ru_{i-1}^0 ;\end{equation} $

当$k>0$时

(2.10) $\begin{equation}\label{10} -ru_{i+1}^{k+1}+(1+2r)u_i^{k+1}-ru_{i-1}^{k+1}=(1-b_1)u_i^k+\sum\limits_{j=1}^{k-1}(b_j-b_{j+1})u_i^{k-j}+b_{k}u_i^0 ;\end{equation}$

(2.11) $ \begin{equation}\label{11} u_i^{k+1}=ru_{i+1}^{k}+(1-2r-b_1)u_i^{k}+ru_{i-1}^{k}+\sum\limits_{j=1}^{k-1}(b_j-b_{j+1})u_i^{k-j}+b_{k}u_i^0 .\end{equation} $

由于古典隐式格式(2.7)是绝对稳定的,但需要求解三对角矩阵.将古典显式格式(2.8)和古典隐式格式相结合,即在奇数时间层上运用古典显式,在偶数时间层上运用古典隐式,得到(2.12)式.这样在每一个双步求解一个含有三对角矩阵的方程组,计算效率将会得到明显改善.

(2.12) $ \begin{equation}\label{14} \left \{\begin{array}{ll} U^{k+1}=[(1-b_1)I-rG_1]U^k+b^k+\sum\limits_{j=2}^{k}c_jU^{k-j+1}+b_kU^0, \\(I+rG_1)U^{k+2}=(1-b_1)U^{k+1}+b^{k+2}+\sum\limits_{j=2}^{k+1}c_jU^{k-j+2}+b_{k+1}U^0 , \end{array} \right. \ k=0, 2, 4, \cdots, \end{equation} $

其中$b^k=[ru_0^k, 0, \cdots, 0, ru_m^k]^T, c_j=b_{j-1}-b_j(j=1, 2, \cdots, n), U^k=[u_1^k, u_2^k, \cdots, u_{m-1}^k]^T$对任意非负值$k$成立, $G_1=\left[\begin{array}{ccccc} 2& - 1&&&\\ - 1&2& - 1&&\\ &\ddots&\ddots&\ddots&\\ && - 1&2& - 1\\ &&& - 1&2\\ \end{array} \right]_{(m-1)\times(m-1)}$, $U^0=[f(x_1), \cdots, f(x_{m-1})]^T$.

引理3.1^[17] 若$\rho>0$,矩阵$A$是非负实阵,则$(I+\rho A)^{-1}$存在且$\|(I+\rho A)^{-1}\|_2\leq1.$

引理3.2 在显-隐格式中定义的$G_1$矩阵是非负定实阵.

证  由于$G_1 + G_1^T=\left[\begin{array}{ccccc} 4& - 2&&&\\ - 2&4& - 2&&\\ &\ddots&\ddots&\ddots&\\ && - 2&4& - 2\\ &&& - 2&4\\ \end{array} \right]_{(m-1)\times(m-1)}$为对角占优矩阵且其对角元素为非负实数,故$G_1$矩阵为非负定矩阵.证毕.

结合引理3.1和引理3.2, $(I+rG_1)^{-1}$存在.可以得到如下结论

定理3.1 时间分数阶慢扩散方程的显-隐格式解是存在唯一的.

运用函数$g(x)=x^{1-\alpha}(x\geq1)$的性质,可得如下一组结论^[13]

(4.1) $\begin{equation}\label{17} 1 = b_0 > b_1 > \cdots \rightarrow0, 1 > 2 - 2^{1 - \alpha} = c_1 > c_2 > \cdots \rightarrow0, \sum\limits_{j=1}^{k}c_j = 1 - b_k, \sum\limits_{j=1}^{\infty}c_j = 1. \end{equation}$

将显式格式(2.11)代入隐式格式(2.10)中消去每个奇数时间层的格式解$u_i^{2k+1}$,可得

(4.2) $ \begin{eqnarray}\label{18} && - ru_{i + 1}^{2k + 2} + (1 + 2r)u_i^{2k + 2} - ru_{i - 1}^{2k + 2}\\ & =& (1 - b_1)u_i^{2k + 1} + \sum\limits_{j=1}^{2k}(b_j - b_{j + 1})u_i^{2k + 1 - j} + b_{2k + 1}u_i^0\\ & =& (1 - b_1)[ru_{i + 1}^{2k} + (1 - 2r - b_1)u_i^{2k} + ru_{i - 1}^{2k} + \sum\limits_{j = 1}^{2k - 1}c_{j + 1}u_i^{2k - j} + b_{2k}u_i^0] \\ &&+ \sum\limits_{j = 1}^{2k}c_{j + 1}u_i^{2k + 1 - j} + b_{2k + 1}u_i^0\\ & =& c_1ru_{i + 1}^{2k} + c_1(c_1 - 2r)u_i^{2k} + c_1ru_{i - 1}^{2k} + c_2u_i^{2k}\\ && + c_1\sum\limits_{j = 1}^{2k - 1}c_{j + 1}u_{i}^{2k - j} + c_1b_{2k}u_{1}^{0} +\sum\limits_{j = 1}^{2k - 1}c_{j + 2}u_i^{2k - j} + b_{2k + 1}u_i^0\\&=& [c_1ru_{i + 1}^{2k} + c_1(c_1 - 2r)u_i^{2k} + c_1ru_{i - 1}^{2k} + c_2u_i^{2k}]\\ && + \sum\limits_{j = 1}^{2k - 1}(c_1c_{j + 1} + c_{j + 2})u_{i}^{2k - j} + c_1b_{2k}u_{1}^{0} + b_{2k + 1}u_i^0. \end{eqnarray} $

设$\widetilde{u}_i^k$为差分格式的近似解,误差$\varepsilon_i^k=\widetilde{u}_i^k-u_i^k, \varepsilon_0^k=\varepsilon_m^k=0, \varepsilon^k=(\varepsilon_1^k, \varepsilon_2^k, \cdots, \varepsilon_{m-1}^k)$.对于$k=0, 1, 2, \cdots, n$,定义如下函数

$ \varepsilon^k(x)=\left \{\begin{array}{ll} \varepsilon_l^k , \;\;&x\in(x_{l-\frac{1}{2}}, x_{l+\frac{1}{2}}], l=1, 2, \cdots , m-1, \\ 0 , & x\in\big[0, \frac{h}{2}\big]\cup\big(L-\frac{h}{2}, L\big] .\end{array} \right.$

对$\varepsilon^k(x)$进行傅立叶展开: $\varepsilon^k(x)=\sum\limits_{j=-\infty}^{+\infty}\nu_j^k{\rm e}^{{\rm i}\frac{2j\pi x}{L}}$$({\rm i}=\sqrt{-1}), k=0, 1, \cdots, n$.其中$\nu_j^k=\frac{1}{L}\int_0^L\varepsilon^k(x){\rm e}^{{\rm i}\frac{2j\pi x}{L}}{\rm d}x, j=0, \pm1, \cdots $.

定义范数$\|\varepsilon^k\|=\sqrt{\sum\limits_{j=1}^{m-1}h|\varepsilon_j^k|^2}$.由于$\varepsilon_0^k=\varepsilon_m^k=0$,有$\|\varepsilon^k\|^2=\int_0^L|\varepsilon^k(x)|^2{\rm d}x=\|\varepsilon^k(x)\|^{2}$.从而利用帕塞瓦尔定理$\|\varepsilon^k(x)\|^2=L\sum\limits_{j=-\infty}^{+\infty}|\nu_j^k|^2$,得出

$\|\varepsilon^k\|^2=\sum\limits_{j=1}^{m-1}h|\varepsilon_j^k|^2=L\sum\limits_{j=-\infty}^{+\infty}|\nu_j^k|^2, \;\; k=0, 1, \cdots , n.$

基于以上分析且$x_l=lh$,可以假设方程误差解的形式为$\varepsilon_l^k=\nu_k{\rm e}^{{\rm i}\lambda lh}(\lambda=\frac{2j\pi}{L})$.

当$n=1$时, $\varepsilon_i^1=r\varepsilon_{i+1}^0+(1-2r)\varepsilon_i^0+r\varepsilon_{i-1}^0, \quad \nu^1=[r{\rm e}^{{\rm i}\lambda h}+(1-2r)+r{\rm e}^{-{\rm i}\lambda h}]\nu^0$.因${\rm e}^{\pm {\rm i}\lambda h}=\cos\lambda h\pm {\rm i}\sin\lambda h, \sin^2\frac{\lambda h}{2}=-\frac{1}{4}({\rm e}^{{\rm i}\lambda h}-2+{\rm e}^{-{\rm i}\lambda h})$,可得

$|\nu^1|=\bigg|1-4r\sin^2\frac{\lambda h}{2}\bigg||\nu^0|\leq C|\nu^0|.$

当$n=2$时,在第一层用显式格式,第二层用隐式格式,即

$\begin{equation}\label{19} u_i^1=ru_{i+1}^0+(1-2r)u_i^0+ru_{i-1}^0 , \end{equation}$

$ \begin{equation}\label{20} -ru_{i+1}^2+(1+2r)u_{i}^2-ru_{i-1}^2=(1-b_1)u_{i}^1+b_1u_i^0 , \end{equation} $

将(4.3)式代入(4.4)式,有

$-ru_{i+1}^2+(1+2r)u_{i}^2-ru_{i-1}^2=c_1ru_{i+1}^0+c_1(1-2r)u_i^0+c_1ru_{i-1}^0+b_1u_i^0, $

$-r\varepsilon_{i+1}^2+(1+2r)\varepsilon_{i}^2-r\varepsilon_{i-1}^2=c_1r\varepsilon_{i+1}^0+c_1(1-2r)\varepsilon_i^0+c_1r\varepsilon_{i-1}^0+b_1\varepsilon_i^0 .$

将$\varepsilon_i^k$代入,得到

$[-r{\rm e}^{{\rm i}\lambda h}+(1+2r)-r{\rm e}^{-{\rm i}\lambda h}]\nu^2=[c_1r{\rm e}^{{\rm i}\lambda h}+c_1(1-2r)+c_1r{\rm e}^{-{\rm i}\lambda h}+b_1]\nu^0, $

则

$\bigg(1+4r\sin^2\frac{\lambda h}{2}\bigg)\nu^2 = \bigg(1-4c_1r\sin^2\frac{\lambda h}{2}\bigg)\nu^0, $

$\bigg |1+4r\sin^2\frac{\lambda h}{2}\bigg||\nu^2| =\bigg|1-4c_1r\sin^2\frac{\lambda h}{2}\bigg||\nu^0|, $

$|\nu^2|=\bigg|\frac{1-4c_1r\sin^2\frac{\lambda h}{2}}{1+4r\sin^2\frac{\lambda h}{2}}\bigg||\nu^0|\leq\bigg|\frac{1+4r\sin^2\frac{\lambda h}{2}}{1+4r\sin^2\frac{\lambda h}{2}}\bigg||\nu^0|=C|\nu^0|. $

假设当$n=2k$时,均有$|\nu^{2k}|\leq C|\nu^0|$,则当$n=2k+2$时, (4.2)式有

$\begin{eqnarray*} [-r{\rm e}^{{\rm i}\lambda h} + (1 + 2r) - r{\rm e}^{-{\rm i}\lambda h}]\nu^{2k + 2} &=& \bigg(c_1^2 + c_2 - 4c_1r\sin^2\frac{\lambda h}{2}\bigg)\nu^{2k} + \sum\limits_{j = 1}^{2k - 1}(c_1c_{j + 1} + c_{j + 2})\nu^0\\&& + c_1b_{2k}\nu^0 + b_{2k + 1}\nu^0, \end{eqnarray*} $

$\begin{eqnarray*} \bigg|1 + 4r\sin^2\frac{\lambda h}{2}\bigg||\nu^{2k + 2}| &\mathop{\leq}\limits^{k\rightarrow\infty}& \bigg|c_1^2 + c_2 - 4c_1r\sin^2\frac{\lambda h}{2}\bigg||\nu^{2k}| + \sum\limits_{j = 1}^{2k - 1}[c_1c_{j + 1} + c_{j + 2}]|\nu^0|\\ &\leq&C\bigg|4c_1r\sin^2\frac{\lambda h}{2}\bigg||\nu^0| + \sum\limits_{j = 1}^{2k}[c_1c_j + c_{j + 1}]|\nu^0|\\&\mathop{=}\limits^{k\rightarrow\infty}&C\bigg|4c_1r\sin^2\frac{\lambda h}{2}\bigg||\nu^0| + |\nu^0|\\&=&C\bigg|1+4c_1r\sin^2\frac{\lambda h}{2}\bigg||\nu^0|\\&\leq& C\bigg|1+4r\sin^2\frac{\lambda h}{2}\bigg||\nu^0|. \end{eqnarray*}$

即$|\nu^{2k+2}|\leq C|\nu^0|$.

根据方程$\|\varepsilon^k\|^2=\sum\limits_{j=1}^{m-1}h|\varepsilon_j^k|^2=L\sum\limits_{j=-\infty}^{+\infty}|\nu_j^k|^2$及上述结论,可以得出: $\|\varepsilon^k\|\leq C\|\varepsilon^0\|, $$k=1, 2, \cdots, n$.因此有如下结论

定理4.1 时间分数阶慢扩散方程的显-隐格式是无条件稳定的.

首先将显、隐两式分别在$u_i^{k+1}$处展开.由于$L_{h, \tau}^\alpha u(x_i, t_{k+1})=\frac{\partial^{\alpha} u(x_i, t_{k+1})} {\partial t^{\alpha}}+O(\tau^{2-\alpha})$ (参见文献[6]),显式格式的截断误差为

$ \begin{eqnarray*} R_{i1}^{k+1} &=&\frac{\partial^\alpha u(x_i, t_{k+1})}{\partial t^\alpha}-\frac{1}{h^2}(u_{i-1}^k-2u_i^k+u_{i+1}^k)\\ &=&\frac{\partial^\alpha u(x_i, t_{k+1})}{\partial t^\alpha}-u_{xx}+\tau u_{xxt}-\frac{\tau^2}{2}u_{xxtt}-\frac{h^2}{12}u_{xxxx}+O(\tau^{2-\alpha}+h^2), \end{eqnarray*} $

隐式格式的截断误差为

$ \begin{eqnarray*} R_{i2}^{k+1} &=&\frac{\partial^\alpha u(x_i, t_{k+2})}{\partial t^\alpha}-\frac{1}{h^2}(u_{i-1}^{k+2}-2u_i^{k+2}+u_{i+1}^{k+2})\\ &=&\frac{\partial^\alpha u(x_i, t_{k+1})}{\partial t^\alpha}+\tau \frac{\partial^{\alpha+1} u(x_i, t_{k+1})}{\partial t^{\alpha+1}}-u_{xx}-\tau u_{xxt}\\&&-\frac{\tau^2}{2}u_{xxtt}-\frac{h^2}{12}u_{xxxx}+O(\tau^{2-\alpha}+h^2). \end{eqnarray*} $

又因为

$ \begin{eqnarray*} \frac{\partial^{\alpha+1} u(x_i, t_{k+1})}{\partial t^{\alpha+1}} &=& \frac{1}{\Gamma(1-\alpha)}\int_0^t\frac{\partial^2u(x_i, \xi)}{\partial\tau^2}\frac{{\rm d}\xi}{(t_{k+1}-\xi)^\alpha}\\ &=& \frac{1}{\Gamma(1-\alpha)}\sum\limits_{j=0}^k\int_{j\tau}^{(j+1)\tau}\frac{\partial^2u(x_i, \xi)}{\partial\xi^2}\frac{{\rm d}\xi}{(t_{k+1}-\xi)^\alpha}\\ &\leq& \frac{1}{\Gamma(1-\alpha)}\max\limits_{t_0\leq t\leq t_{k+1}}{\mid u_{tt}\mid}\sum\limits_{j=0}^k\int_{j\tau}^{(j+1)\tau}\frac{{\rm d}\xi}{(t_{k+1}-\xi)^\alpha}\\ &=& \frac{c_u\tau^{1-\alpha}}{(1-\alpha)\Gamma(1-\alpha)}\sum\limits_{j=0}^k[(k+1-j)^{1-\alpha}-(k-j)^{1-\alpha}]\\ &=&O(\tau^{1-\alpha}) , \end{eqnarray*} $

得到$\tau\frac{\partial^{\alpha+1} u(x_i, t_{k+1})}{\partial t^{\alpha+1}}\leq C\tau^{2-\alpha}, C>0.$另外显式和隐式格式在交替使用时$\tau u_{xxt}$项会被抵消,所以显隐格式精度在空间上2阶,在时间上$2-\alpha$阶.

假设$\widetilde{U}_j^k$是微分方程的解, $U_j^k$是差分方程的解,有

(5.1) $\begin{equation}\label{21} \left \{\begin{array}{ll} E_l^1=rE_{l+1}^0+(1-2r)E_l^0+rE_{l-1}^0+\tau^{\alpha}R_l^1, \\ -rE_{l+1}^2+(1+2r)E_l^2-rE_{l-1}^2=c_1rE_{l+1}^0+c_1(1-2r)E_l^0+c_1rE_{l-1}^0+b_1E_l^0+\tau^\alpha R_l^2, \\ -rE_{l+1}^{2k+2}+(1+2r)E_l^{2k+2}-rE_{l-1}^{2k+2}=c_1rE_{l+1}^{2k}+c_1(c_1-2r)E_l^{2k}+c_1rE_{l-1}^{2k}+c_2E_l^{2k}\\ \;\;\;\;\;+\sum\limits_{j=1}^{2k-1}(c_1c_{j+1}+c_{j+2})E_l^{2k-j}+c_1b_{2k}E_l^0+b_{2k+1}E_l^0+\tau^\alpha R_l^{2k+2} , \end{array} \right. \end{equation} $

其中$E_l^k=U_l^k-\widetilde{U}_l^k, R_l^k=O(\tau^{2-\alpha}+h^2)$,且$E_0^k=E_m^k=0, E_l^0=0, k=0, 1, \cdots, n, $$l=0, 1, \cdots, m$.

同稳定性证明,定义两个网格函数

$ E^k(x)=\left \{\begin{array}{ll} E_l^k ,& x\in(x_{l-\frac{1}{2}}, x_{l+\frac{1}{2}}], l=1, 2, \cdots , m-1, \\ 0 , \;\;\;& x\in[0, \frac{h}{2}]\cup(L-\frac{h}{2}, L], \end{array} \right.$

$R^k(x)=\left \{\begin{array}{ll}R_l^k, \;\;\;\;&x\in(x_{l-\frac{1}{2}}, x_{l+\frac{1}{2}}], l=1, 2, \cdots , m-1, \\ 0 ,& x\in[0, \frac{h}{2}]\cup(L-\frac{h}{2}, L] , \end{array} \right. $

且$E^k(x)$和$R^k(x)$有傅里叶展开: $E^k(x)=\sum\limits_{j=-\infty}^{+\infty}E_j^k{\rm e}^{{\rm i}\frac{2j\pi x}{L}}$和$R^k(x)=\sum\limits_{j=-\infty}^{+\infty}R_j^k{\rm e}^{{\rm i}\frac{2j\pi x}{L}}, $$k=0, 1, \cdots, n, $$j=0, \pm1, \cdots $.

定义范数$\|E^k\|=\sqrt{\sum\limits_{j=1}^{m-1}h|E_j^k|^2}, \|R^k\|=\sqrt{\sum\limits_{j=1}^{m-1}h|R_j^k|^2}$.同理假设$E_l^k={\rm e}^k{\rm e}^{{\rm i}\lambda lh}, $$R_l^k=r^k{\rm e}^{{\rm i}\lambda lh}(\lambda=\frac{2\pi j}{L}), $$x_l=lh$.代入(5.1)式中,有

(5.2) $\begin{equation}\label{22} \left \{\begin{array}{ll} e^1=\tau^{\alpha}r^1, \\ {}[-r{\rm e}^{{\rm i}\lambda h}+(1+2r)-r{\rm e}^{-{\rm i}\lambda h}]e^2=\tau^\alpha r^2, \\ {}[-r{\rm e}^{{\rm i}\lambda h}+(1+2r)-r{\rm e}^{-{\rm i}\lambda h}]{\rm e}^{2k+2}=[c_1r{\rm e}^{{\rm i}\lambda h}+c_1(c_1-2r)+c_1r{\rm e}^{-{\rm i}\lambda h}+c_2]{\rm e}^{2k}\\ +\sum\limits_{j=1}^{2k-1}(c_1c_{j+1}+c_{j+2}){\rm e}^{2k-j}+\tau^\alpha r^{2k+2}, l=1, 2, \cdots , m-1, k\geq1 .\end{array} \right. \end{equation} $

由于$\sin^2\frac{z}{2}=-\frac{1}{4}({\rm e}^{{\rm i}z}-2+{\rm e}^{-{\rm i}z})$, (5.2)式可得

(5.3) $\begin{equation}\label{23} \left \{\begin{array}{ll} e^1=\tau^{\alpha}r^1, \\\bigg(1+4r\sin^2\frac{\lambda h}{2}\bigg)e^2=\tau^\alpha r^2, \\ \bigg (1+4r\sin^2\frac{\lambda h}{2}\bigg){\rm e}^{2k+2}=\bigg[c_1^2+c_2-4c_1\sin^2\frac{\lambda h}{2}\bigg]{\rm e}^{2k}\\\;\;\;\;+\sum\limits_{j=1}^{2k-1}(c_1c_{j+1}+c_{j+2}){\rm e}^{2k-j}+\tau^\alpha r^{2k+2}, \;\;\;l=1, 2, \cdots , m-1, k\geq1.\end{array} \right. \end{equation}$

引理5.1 设$e^k$为(5.2)式的解,则$\exists C_1>0$,使得$|{\rm e}^{2k+2}|\leq C_1b_{2k}^{-1}\tau^\alpha|r^1|, k=0, 1, \cdots $.

证  由于$R_l^k=O(\tau^{2-\alpha}+h^2)$,故$\exists G_2>0$,使$|R_l^k|\leq C_2(\tau^{2-\alpha}+h^2)$.根据式$\|R^k\|^2=\sum\limits_{j=1}^{m-1}h|R_j^k|^2=L\sum\limits_{j=-\infty}^{+\infty}|R_j^k|^2$,有$\|R^k\|\leq C_2\sqrt{L}(\tau^{2-\alpha}+h^2), |r^k|\equiv|R_l^k|\leq C_3|R_l^1|\equiv C_3|r^1|, $$k=1, 2, \cdots, n, C_3>0$.对(5.3)式有

$|e^1|\leq\tau^\alpha|r^1|=b_0^{-1}\tau^\alpha|r^1|, \quad|e^2|=\frac{|\tau^\alpha r^2|}{|1+4r\sin^2\frac{\lambda h}{2}|}\leq C_3\tau^\alpha|r^1|=C_3b_0^{-1}\tau^\alpha|r^1|.$

假设$|{\rm e}^{2k}|\leq C_1b_{2k-2}^{-1}\tau^\alpha|r^1|, C_1=\max{(1, C_3)}$,有

$\begin{eqnarray*} \bigg|1 + 4r\sin^2\frac{\lambda h}{2}\bigg||{\rm e}^{2k + 2}| &\leq&\bigg |\bigg(c_1^2 + c_2 - 4c_1r\sin^2\frac{\lambda h}{2}\bigg){\rm e}^{2k} \\&&+ \sum\limits_{j = 1}^{2k - 1}(c_1c_{j + 1} + c_{j + 2}){\rm e}^{2k - j}\bigg| + \tau^\alpha|r^{2k+2}|\\ &\leq& C_3\tau^\alpha|r^1| + \sum\limits_{j = 1}^{2k}(c_1c_j + c_{j + 1})|{\rm e}^{2k - j + 1}| + 4c_1r\sin^2\frac{\lambda h}{2}|{\rm e}^{2k}|\\ &\leq& \bigg(c_1 + \sum\limits_{j = 1}^{2k}c_{j + 1} + 4c_1r\sin^2\frac{\lambda h}{2} + b_{2k}\bigg)C_1b_{2k}^{-1}\tau^\alpha|r^1|\\ &\mathop{\leq}\limits^{k\rightarrow\infty}&\bigg (1 + 4c_1r\sin^2\frac{\lambda h}{2}\bigg)C_1b_{2k}^{-1}\tau^\alpha|r^1|. \end{eqnarray*} $

因此$|{\rm e}^{2k+2}|\leq C_1b_{2k}^{-1}\tau^\alpha|r^1|$.证毕.

由于$\lim\limits_{k\rightarrow\infty} \frac{b_k^{-1}}{k^{\alpha}}=\frac{1}{1-\alpha}$,因此$b_{k-2}^{-1}k^{-\alpha}\leq b_{k}^{-1}k^{-\alpha}\mathop{=}\limits^{k\rightarrow+\infty}\frac{1}{1-\alpha}$,则有

$|e^k|\leq C_1b_{k-2}^{-1}\tau^\alpha|r^1|=C_1b_{k-2}^{-1}k^{-\alpha}k^{\alpha}\tau^{\alpha}|r^1|\leq\frac{C_1}{1-\alpha}(k\tau)^{\alpha}|r^1|\leq\frac{C_1}{1-\alpha}T^\alpha|r^1|.$

根据帕塞瓦尔定理可得: $\|E^k\|\leq\frac{C_1}{1-\alpha}T^\alpha\|R^1\|\leq\frac{C_1}{1-\alpha}T^\alpha C_2\sqrt{L}(\tau^{2-\alpha}+h^2)=C(\tau^{2-\alpha}+h^2)$.

定理5.1 时间分数阶慢扩散方程的显-隐格式是无条件收敛的,且

$\|U^k-\widetilde{U}^k\|\leq C(\tau^{2-\alpha}+h^2), \;\;\;k=1, 2, \cdots , n, C>0.$

类似地,给出时间分数阶慢扩散方程(2.1)的隐-显格式,即在求解奇数时间层时用隐式格式,在偶数层上用显式格式,得到如下隐-显格式

(6.1) $ \begin{equation}\label{25} \left \{\begin{array}{ll} (I+rG_1)U^{k+1}=(1-b_1)U^k+b^{k+1}+\sum\limits_{j=2}^{k}c_jU^{k-j+1}+b_kU^0, \\ U^{k+2}=[(1-b_1)I-rG_1]U^{k+1}+b^{k+1}+\sum\limits_{j=2}^{k+1}c_jU^{k-j+2}+b_{k+1}U^0 , \end{array} \right. \ k=0, 2, 4, \cdots, \end{equation} $

其中$G_1$及$b_k$的定义同显-隐格式.

由于第一时间层的隐式格式是无条件稳定且收敛的^[13],则从第二时间层开始同显-隐格式的分析证明,有如下定理

定理6.1 时间分数阶慢扩散方程的隐-显格式是无条件稳定和收敛的,且

$\|U^k-\widetilde{U}^k\|\leq C(\tau^{2-\alpha}+h^2), \;\;\;k=1, 2, \cdots , n, C>0.$

数值试验基于Intel Core i5-2400 CPU,在MatlabR2014b环境下进行.

考虑如下时间分数阶慢扩散方程^[13]

$\frac{\partial^\alpha u(x, t)}{\partial t^\alpha}=\frac{\partial^2 u(x, t)}{\partial x^2}, \;\;\; 0\leq x\leq 2, t>0, $

在边界条件$u(0, t)=u(2, t)=0$,初始条件$ u(x, 0)=f(x)=\left \{\begin{array}{ll} 2x, & 0\leq x\leq0.5, \\ \frac{4-2x}{3}, \; \; \; & 0.5\leq x\leq2.\end{array} \right. $

在$t=0.4, \alpha=0.5$处,将本文格式数值解与精确解以及隐式(Implicit)格式的数值解^[13]相比较.取$n=500, m=500$,计算结果和时间如表 1,其中精确解时间为在$t=0.4$处的计算时间.

由表 1可以看出,本文构造的显-隐格式及隐-显格式的数值解比隐式格式解可以更好地逼近解析解.根据计算时间,相比于解析解,数值格式的CPU时间有着很大的优势.时间分数阶慢扩散方程解析解的计算量是非常庞大的,且我们只关心解析解在$t=0.4$处的数值及时间,其CPU时间约为174.60s.而两种格式数值解的整体CPU时间分别为6.73s和3.88s,且本文格式的计算效率比隐式提高了75%,因此该方法是解决分数阶慢扩散方程的一种有效的差分方法.

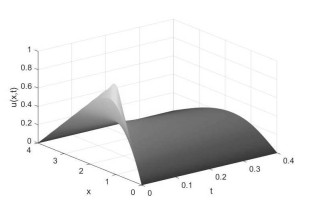
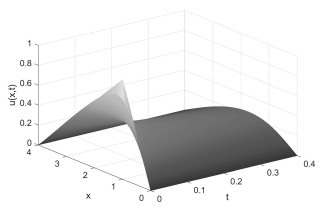
图 1和图 2比较了解析解与显-隐格式数值解曲面,可以看出它们是一致的且格式解曲面非常光滑.为了验证本文格式稳定性,给出相对误差随时间推移的变化情况.令格式数值解$\widetilde{U}_i^j$为扰动解,精确解$U_i^j$为控制解,定义相对误差SRET (the sum of relative error for every time level)

$SRET(j)=\sum\limits_{i=1}^{m}\frac{|\widetilde{U}_i^j-U_i^j|}{U_i^j}, $

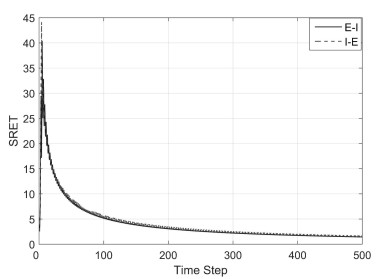
如图 3可以看出,虽然显-隐格式与隐-显格式的相对误差在初始时数值较大,但随着时间步数的变化误差迅速下降,两曲线变化相近且仍有下降趋势,且E-I格式相比I-E格式的误差更小.由于实际问题中只关心$t=0.4$时解的情况,因此可以得出时间分数阶慢扩散方程的显-隐格式是稳定的且有着良好的精度.由于显-隐与隐-显格式的解及相对误差值相近,因此以下分析显-隐格式.

定义误差的$L^2$模以及空间层收敛阶Order1和时间层收敛阶Order2如下^{[11, 18]}

$E_{2, h}^n=\|U_i^n-\widetilde{U}_i^n\|_2=\bigg\{\sum\limits_{i=1}^{m}(U_i^n-\widetilde{U}_i^n)^2h\bigg\}^{\frac{1}{2}} , \quad E_{2, \tau}^n=\|U_i^n-\widetilde{U}_i^n\|_2=\bigg\{\sum\limits_{i=1}^{m}(U_i^n-\widetilde{U}_i^n)^2\tau\bigg\}^{\frac{1}{2}}, $

${\rm Order1}=\log_{2}{(E_{2, h}^n/E_{2, h/2}^n)}, \quad{\rm Order2}=\log_{2}{(E_{2, \tau}^n/E_{2, \tau/2}^n)}, $

表 2和表 3分别求解了隐式格式和显-隐格式的计算误差和空间收敛阶以及在$\alpha$取不同值时的时间收敛阶.结果表明本文格式计算误差比隐式格式小,同时计算精度在空间上二阶,时间上$2-\alpha$阶,与理论分析是一致的.

最后将时间数值层数固定,比较分析空间网格点的增加对三种差分格式计算时间的影响.选取时间网格数和空间网格数分别为: $n=1000;$$ m=100, 200, 300, 400, 500, 600, 700, 800, $$ 900, 1000.$比较结果如图 4.

可以看出虽然在空间网格点数较小时本文格式的计算时间比隐式格式略大,但随着空间网格数的增加隐式格式的计算时间迅速增加且变化率较大,而本文构造的格式计算时间变化率较小且不大于$20s$,因此在精度相近的情况下显-隐格式和隐-显格式较隐式格式计算效率更高.

本文构造了时间分数阶慢扩散方程的显-隐(E-I)和隐-显(I-E)格式,理论证明了格式是无条件稳定且收敛的,在计算精度与隐式格式相当的情况下其计算效率随着差分网格数的增加有着明显提高.数值试验验证了理论分析,表明了用显-隐和隐-显差分格式求解时间分数阶慢扩散方程是有效的.