时间分数阶慢扩散方程的一类有效差分方法

摘要/Abstract

摘要：

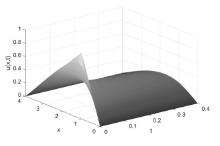
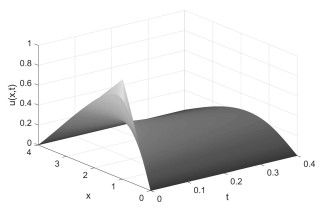
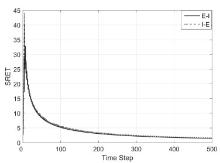
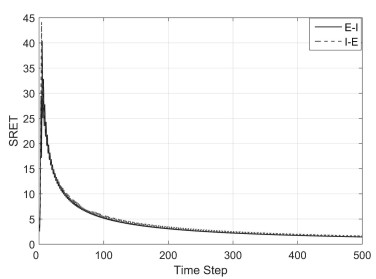
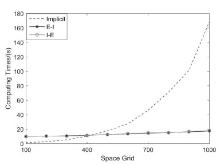
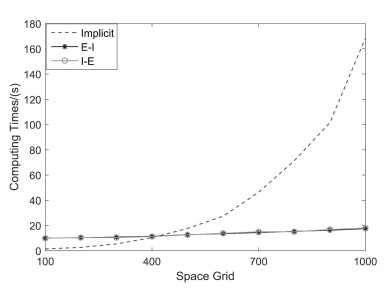
对时间分数阶慢扩散方程提出一类数值差分方法：显-隐（Explicit-Implicit，E-I）和隐-显（Implicit-Explicit，I-E）差分方法.它是将古典显式格式与古典隐式格式相结合构造出的一类有效差分格式.理论证明了格式解的存在唯一性，用傅里叶方法证明了格式的稳定性和收敛性.数值试验验证了理论分析，表明E-I格式和I-E格式在具有良好的精度且无条件稳定的情况下，计算速度比隐式格式提高了75%.从而用此格式解决分数阶慢扩散方程是可行的.

关键词: 时间分数阶慢扩散方程, 显-隐(隐-显)差分格式, 稳定性, 收敛性, 数值试验

Abstract:

In this paper, a kind of numerical difference method of explicit-implicit(E-I) scheme and implicit-explicit(I-E) scheme was constructed for solving the time fractional sub-diffusion equation. It is based on the combination of the explicit scheme and implicit scheme. Theoretical analyses have shown that the solution of E-I(I-E) scheme is uniquely solvable. At the same time the stability and convergence of the scheme were proved by the Fourier method. Numerical experiments verified the theoretical analyses and showed the computational efficiency of E-I scheme is 75% higher than the implicit scheme under the premise of unconditional stability and having better accuracy. Therefore it is feasible to use the scheme for solving the time fractional diffusion equation.

Key words: Time fractional sub-fractional equation, Explicit-implicit (implicit-explicit) difference scheme, Stability, Convergence, Numerical experiments

中图分类号:

O241.8

赵雅迪, 吴立飞, 杨晓忠, 孙淑珍. 时间分数阶慢扩散方程的一类有效差分方法[J]. 数学物理学报, 2018, 38(6): 1122-1134.

Yadi Zhao, Lifei Wu, Xiaozhong Yang, Shuzhen Sun. A Kind of Efficient Difference Method for the Time Fractional Sub-Diffusion Equation[J]. Acta mathematica scientia,Series A, 2018, 38(6): 1122-1134.

图/表 7

表 1

图 1

图 2

图 3

表 2

E-I格式的误差和空间收敛阶( $\tau=h^2$ )"

	Implicit		E-I
$m$	$L_{h, \tau}^2$	Order1	$L_{h, \tau}^2$	Order1
20	2.593343e-3	—	2.958102e-3	—
40	6.548375e-4	1.985604	6.245729e-4	2.243741
80	1.667856e-4	1.973142	1.418638e-4	2.138363
160	4.221036e-5	1.982326	3.564083e-5	1.992904
320	1.057340e-5	1.997158	8.933510e-6	1.996232

表 2

表 3

E-I格式的误差和时间收敛阶 $(m=80)$ "

		Implicit		E-I
$\alpha$	$n$	$L_{h, \tau}^2$	Order2	$L_{h, \tau}^2$	Order2
$0.7$	200	2.545864e-4	—	1.094796e-4	—
	400	1.047661e-4	1.280984	4.699933e-5	1.219950
	800	4.284855e-5	1.289853	2.031905e-5	1.209807
	1600	1.746390e-5	1.294870	8.822774e-6	1.203529
	3200	7.102732e-6	1.297930	3.842242e-6	1.199284
$0.5$	200	8.475178e-5	—	3.620591e-5	—
	400	3.023084e-5	1.487222	1.351384e-5	1.421788
	800	1.072535e-5	1.494997	5.109668e-6	1.403136
	1600	3.788677e-6	1.501259	1.950831e-6	1.389141
	3200	1.332788e-6	1.507247	7.514643e-7	1.376312
$0.4$	200	4.222321e-5	—	1.920942e-5	—
	400	1.399031e-5	1.593609	6.639797e-6	1.532603
	800	4.601493e-6	1.604254	2.352434e-6	1.496985
	1600	1.501415e-6	1.615779	8.522910e-7	1.464736
	3200	4.849225e-7	1.630497	3.161945e-7	1.430534

表 3

图 4

参考文献 18

1	Metzler R , Klafter J . The random walk's guide to anomalous diffusion:a fractional dynamics approach. Physics Reports, 2000, 339 (1): 1- 77
2	陈文, 孙洪广, 李西成, 等. 力学与工程问题的分数阶导数建模. 北京: 科学出版社, 2010
	Chen W , Sun H G , Li X C , et al. Fractional Derivative Modeling of Mechanics and Engineering Problems. Beijing: Science Press, 2010
3	Vladimir V , Uchaikin . Fractional Derivatives for Physicist and Engneers, Volume Ⅱ:Applications. New York: Springer, 2013
4	Li J , Guo B L . Parameter identification in fractional differential equations. Acta Mathematica Scientia, 2013, 33 (3): 855- 864 doi: 10.1016/S0252-9602(13)60045-4
5	Guo B L , Pu X K , Huang F H . Fractional Partial Differential Equations and Their Numerical Solutions. Beijing: Science Press, 2015
6	孙志忠, 高广花. 分数阶微分方程的有限差分方法. 北京: 科学出版社, 2015
	Sun Z Z , Gao G H . Finite Difference Methods for Fractional Differential Equations. Beijing: Science Press, 2015
7	覃平阳, 张晓丹. 空间-时间分数阶对流扩散方程的数值解法. 计算数学, 2008, 30 (3): 305- 310 doi: 10.3321/j.issn:0254-7791.2008.03.008
	Tan P Y , Zhang X D . Numerical solution of space-time fractional convection diffusion equation. Computational Mathematics, 2008, 30 (3): 305- 310 doi: 10.3321/j.issn:0254-7791.2008.03.008
8	Tadjeran C , Meerschaert Mark M , Scheffler H P . A second-order accurate numerical approximation for the fraction diffusion equation. Journal of Computational Physics, 2006, 213 (1): 205- 213 doi: 10.1016/j.jcp.2005.08.008
9	Zhao Y , Zhang Y , Liu F , et al. Convergence and superconvergence of a fully-discrete scheme for multi-term time fractional diffusion equations. Computers and Mathematics with Applications, 2017, 73 (6): 1087- 1099 doi: 10.1016/j.camwa.2016.05.005
10	Chen C M , Liu F , Burrage K . Finite difference methods and a fourier analysis for the fractional reaction-subdiffusion equation. Applied Mathematics and Computation, 2008, 198 (2): 754- 769 doi: 10.1016/j.amc.2007.09.020
11	Gao G H , Sun Z Z . A compact finite difference scheme for the fractional sub-diffusion equations. Journal of Computational Physics, 2011, 230 (3): 586- 595 doi: 10.1016/j.jcp.2010.10.007
12	Liu F , Shen S , Anh V , et al. Analysis of a discrete non-Markovian random walk approximation for the time fractional diffusion equation. Anziam Journal, 2005, 46 (E): C488- C504
13	Shen S , Liu F , Anh V , et al. Implicit difference approximation for the time fractional diffusion equation. Journal of Applied Mathematics and Computing, 2006, 22 (3): 87- 99 doi: 10.1007/BF02832039
14	Yuste S B . Weighted average finite difference methods for fractional diffusion equations. Journal of Computational Physics, 2004, 216 (1): 264- 274
15	Yuste S B , Acedo L . An explicit finite difference method and a new Von Neumann-type stability analysis for fractional diffusion equations. Siam Journal on Numerical Analysis, 2006, 42 (5): 1862- 1874
16	Lin Y , Xu C . Finite difference/spectral approximations for the time-fractional diffusion equation. Journal of Computational Physics, 2007, 225 (2): 1533- 1552 doi: 10.1016/j.jcp.2007.02.001
17	张宝琳, 袁国兴, 刘兴平. 偏微分方程并行有限差分方法. 北京: 科学出版社, 1994
	Zhang B L , Yuan G X , Liu X P . Parallel Finite Difference Methods for Partial Differential Equations. Beijing: Science Press, 1994
18	Zhang Y N , Sun Z Z , Wu H W . Error estimates of Crank-Nicolson-type difference schemes for the sub-diffusion equation. SIAM Journal on Numerical Analysis, 2011, 49 (6): 2302- 2322 doi: 10.1137/100812707

相关文章 15

[1]	章志华,陈平炎. $φ$ -混合序列加权和的完全收敛性[J]. 数学物理学报, 2018, 38(6): 1095-1102.
[2]	朱志锋,张绍义. 用概率距离研究非时齐马氏链的收敛性[J]. 数学物理学报, 2018, 38(5): 963-969.
[3]	王丹妮,杨红丽,杨联贵. 一类完整Coriolis力作用下的高阶非线性Schrödinger方程的推导[J]. 数学物理学报, 2018, 38(5): 883-892.
[4]	谷海波,高彩霞. 基于Razumikhin-Type理论的中立性随机切换非线性系统的P阶矩稳定性与几乎必然稳定性[J]. 数学物理学报, 2018, 38(5): 970-983.
[5]	郑立飞,郭洁,吴美华,王小瑞,万阿英. 一类具有时滞的捕食者-猎物-共生者系统的研究[J]. 数学物理学报, 2018, 38(5): 1001-1013.
[6]	吴斌, 高莹, 闫林, 余军. 一类带有非奇异主部系数矩阵的2×2强耦合偏微分系统的卡勒曼估计及其反源问题[J]. 数学物理学报, 2018, 38(4): 779-799.
[7]	杨轩, 阮小娥, 王彭. 时变切换信号驱动的线性连续切换系统的迭代学习控制收敛性分析[J]. 数学物理学报, 2018, 38(3): 599-612.
[8]	王军礼, 张兴伟, 刘健. 可压缩Navier-Stokes方程平面Couette-Poiseuille流的线性不稳定性[J]. 数学物理学报, 2018, 38(2): 322-333.
[9]	王晚生, 钟鹏, 赵新阳. 非线性中立型变延迟微分方程的长时间稳定性[J]. 数学物理学报, 2018, 38(1): 96-109.
[10]	孟笑莹. 具有非单调发生率的时滞随机传染病模型分析[J]. 数学物理学报, 2017, 37(6): 1162-1175.
[11]	李海侠. 一类食物链模型正解的稳定性和唯一性[J]. 数学物理学报, 2017, 37(6): 1094-1104.
[12]	王春, 许天周. 拟Banach空间上含参数的二次-可加混合型函数方程的解和Hyers-Ulam-Rassias稳定性[J]. 数学物理学报, 2017, 37(5): 846-859.
[13]	陈红斌, 甘四清, 徐大, 彭玉龙. 二维分数阶发展型方程的正式的二阶BDF交替方向隐式紧致差分格式[J]. 数学物理学报, 2017, 37(5): 976-992.
[14]	杨纪华, 张二丽, 刘媚. 具时滞反馈金融系统的动力学分析与混沌控制[J]. 数学物理学报, 2017, 37(4): 767-782.
[15]	熊君, 李俊民, 何超. 一阶双曲型偏微分方程的模糊边界控制[J]. 数学物理学报, 2017, 37(3): 469-477.

Metrics

Viewed

Full text

150

HTML			PDF

Just accepted	Online first	Issue	Just accepted	Online first	Issue
0	0	1	0	0	149

From	Others	local

Times	4	146
Rate	3%	97%

Abstract

Just accepted	Online first	Issue

0	0	94

	From	Others

	Times	95
	Rate	100%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed

	0.25	0.5	0.75	1	1.25	1.5	1.75	时间/s
精确解	0.1097	0.1946	0.2356	0.2351	0.2030	0.1487	0.0787	174.6007
隐式格式解	0.1090	0.1933	0.2339	0.2334	0.2014	0.1476	0.0781	6.7294
E-I格式解	0.1100	0.1951	0.2362	0.2358	0.2036	0.1492	0.0790	3.8812
I-E格式解	0.1100	0.1952	0.2363	0.2359	0.2037	0.1493	0.0790	3.8755