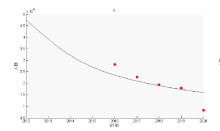
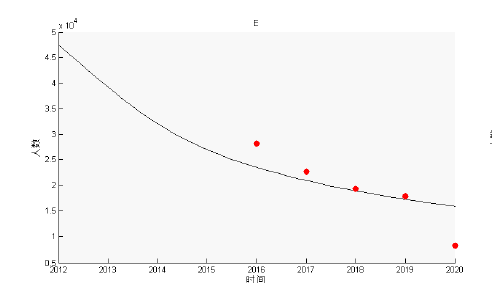
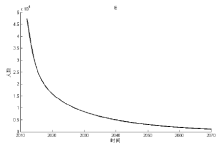
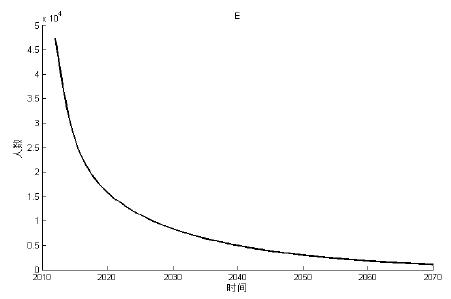
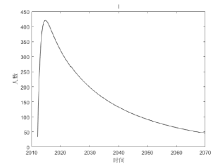
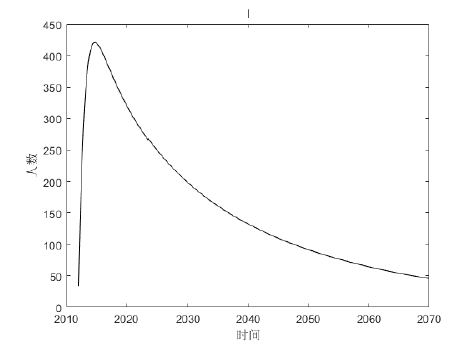
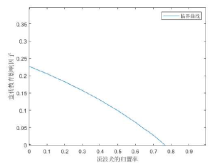
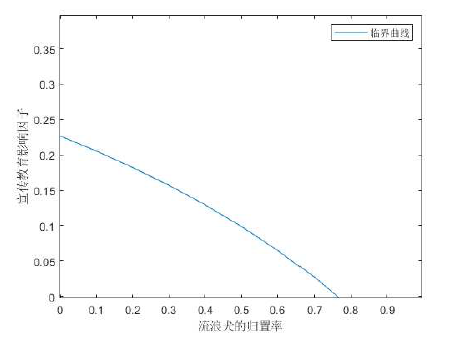
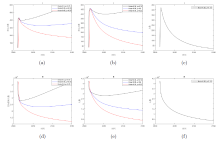
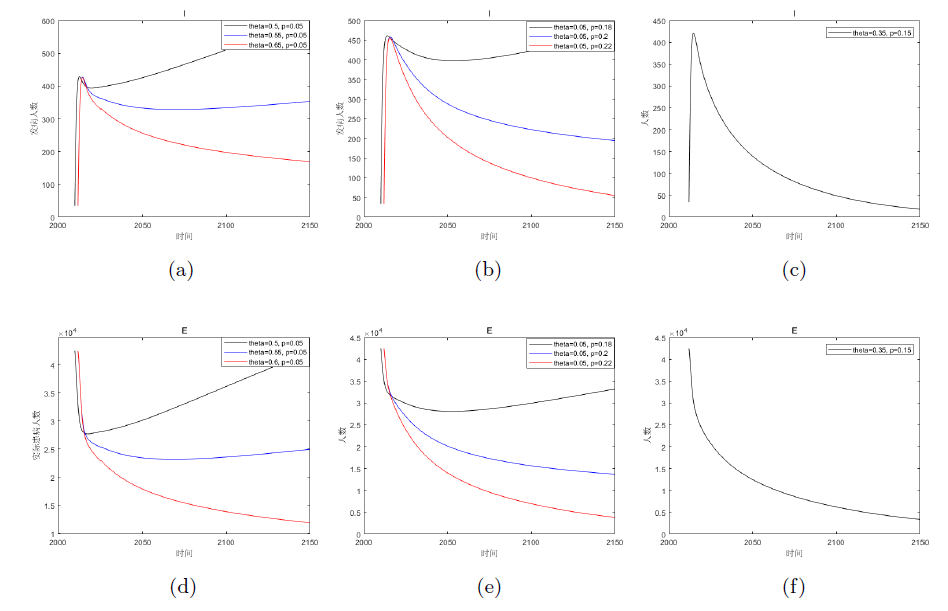
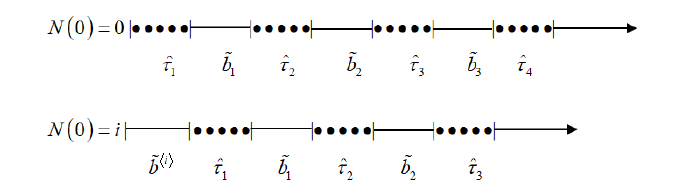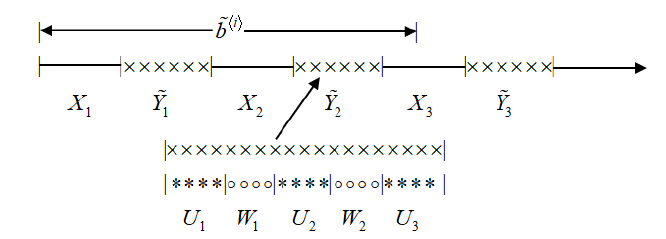Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (2): 646-656.
Mathematical Modeling and Dynamic Analysis of Echinococcosis Transmission in Tibet Autonomous Region
- College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070
-
Received:2022-01-29Revised:2022-10-17Online:2023-04-26Published:2023-04-17 -
Supported by:NSFC(12161079);Natural Science Foundation of Gansu Province(20JR10RA086)
CLC Number:
- O175.1
Cite this article
Xu Yue, Han Xiaoling. Mathematical Modeling and Dynamic Analysis of Echinococcosis Transmission in Tibet Autonomous Region[J].Acta mathematica scientia,Series A, 2023, 43(2): 646-656.
share this article
| [1] |
Eckert J, Deplazes P. Biological, epidemiological, and clinical aspects of echinococ-cosis, a zoonosis of increasing concern. Clin Microbiol Rev, 2004, 17(1): 107-135
doi: 10.1128/CMR.17.1.107-135.2004 |
| [2] |
Davidson R K, Romig T, Jenkins E, et al. The impact of globalisation on the distribution of Echinococcus multilocularis. Trends Parasitol, 2012, 28(6): 239-247
doi: 10.1016/j.pt.2012.03.004 pmid: 22542923 |
| [3] | 陈伟奇, 张雅兰, 贡桑曲珍, 等. 西藏自治区棘球蚴病病例分析. 中国寄生虫学与寄生虫病杂志, 2018, 36(1): 43-46 |
| Chen W Q, Zhang Y L, GongSang Q Z, et al. Analysis of hydatid disease cases in Tibet Autonomous Region. Chinese Journal of Parasitology and Parasitic Diseases, 2018, 36(1): 43-46 | |
| [4] | 韩帅, 蒉嫣, 薛垂召, 等. 2004-2020年全国棘球蚴病疫情分析. 中国寄生虫学与寄生虫病杂志, 2021, 39(5): 1-6 |
| Han S, Kuai Y, Xue C Z, et al. The endemic status of echinococcosis in China from 2004 to 2020. Chinese Journal of Parasitology and Parasitic Diseases, 2021, 39(5): 1-6 | |
| [5] | 蒉嫣, 伍卫平, 韩帅, 等. 2018-2019年全国棘球蚴病监测分析. 中国病原生物学杂志, 2021, 16(9): 1025-1029 |
| Kuai Y, Wu W P, Han S, et al. Analysis of the results of echinococcosis surveillance in China from 2018 to 2019. Journal of Pathogen Biology, 2021, 16(9): 1025-1029 | |
| [6] |
Gemmell M A, Lawson J R, Roberts M G. Population dynamics in echinococcosis and cysticercosis: biological parameters of Echinococcus granulosus in dogs and sheep. Parasitology, 1986, 92(3): 599-620
doi: 10.1017/S0031182000065483 |
| [7] |
Roberts M G, Lawson J R, Gemmell M A. Population dynamics in echinococcosis and cysticercosis: mathematical model of the life-cycle of Echinococcus granulosus. Parasitology, 1986, 92(3): 621-641
doi: 10.1017/S0031182000065495 |
| [8] | 杜守洪, 王蕾, 张学良, 等. 一类具有饱和发生率的包虫病传播模型研究. 数学的实践与认识, 2013, 43(20): 269-273 |
| Du S H, Wang L, Zhang X L, et al. A Echinococcosis model with saturation incidence. Journal of Mathematics in Practice and Theory, 2013, 43(20): 269-273 | |
| [9] |
Liu J, Liu L, Feng X, et al. Global dynamics of a time-delayed echinococcosis transmission model. Advances in Difference Equations, 2015, 2015(1): 1-16
doi: 10.1186/s13662-014-0331-4 |
| [10] | Xu Z, Ai C. A spatial echinococcosis transmission model with time delays: stability and traveling waves. International Journal of Biomathematics, 2017, 10(6): 1-32 |
| [11] | 赵瑜, 杨诗杰. 一类随机包虫病传播模型及CDC数据拟合. 生物数学学报, 2017, 32(1): 41-48 |
| Zhao Y, Yang S J. Modeling a stochastic Echinococcosis transmission and fitting the statistical data of CDC. Journal of Biomathematics, 2017, 32(1): 41-48 | |
| [12] |
Rong X M, Fan M, Sun X D, et al. Impact of disposing stray dogs on risk assessment and control of Echinococcosis in Inner Mongolia. Mathematical Biosciences, 2018, 299: 85-96
doi: S0025-5564(17)30436-4 pmid: 29526551 |
| [13] |
Wang K, Zhang X, Jin Z, et al. Modeling and analysis of the transmission of Echinococcosis with application to Xinjiang Uygur Autonomous Region of China. Journal of Theoretical Biology, 2013, 333: 78-90
doi: 10.1016/j.jtbi.2013.04.020 pmid: 23669505 |
| [14] | 唐丹丹. 新疆地区包虫病模型的建立与仿真. 乌鲁木齐: 新疆医科大学, 2016 |
| Tang D D. The Establishment and Simulation of Echinococcosis Model in Xinjiang. Urumqi: Xinjiang Medical University, 2016 | |
| [15] | Zhang Y, Xiao Y. Modeling and analyzing the effects of fixed-time intervention on transmission dynamics of echinococcosis in Qinghai province. Mathematical Methods in the Applied Sciences, 2018, 76: 1249-1267 |
| [16] |
Dreessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences, 2002, 180: 29-48
pmid: 12387915 |
| [17] | 刘平, 吴海荣, 张伟超, 等. 我国西部地区农牧民包虫病防控认知情况及其影响因素. 中国动物检疫, 2021, 38(5): 1-4 |
| Liu P, Wu H R, Zhang W C, et al. Awareness of herdsmen for the prevention and control of echinococcosis and potential risk factors in western china. China Animal Health Inspection, 2021, 38(5): 1-4 | |
| [18] | 马知恩, 周义仓, 王稳地, 靳帧. 传染病动力学的数学建模与研究. 北京: 科学出版社, 2004 |
| Ma Z E, Zhou Y C, Wang W D, Jin Z. Mathematical Modeling and Research on the Dynamics of Infectious Diseases. Beijing: Science Press, 2004 |
| [1] | Wenli Zheng,Jia Tang,Cairong Chen. A Dynamic Model for a Class of New Generalized Absolute Value Equations [J]. Acta mathematica scientia,Series A, 2022, 42(3): 818-825. |
| [2] | Yongjian Liu,Qiujian Huang. Jacobi Analysis of the Rabinovich System [J]. Acta mathematica scientia,Series A, 2021, 41(3): 783-796. |
| [3] | FENG Chun-Hua. Oscillatory Behavior for a Simplified n-neuron BAM Neural Networks Model with Time Delays [J]. Acta mathematica scientia,Series A, 2011, 31(6): 1490-1501. |
| [4] | Yuan Xiaofeng Guo Ruihai Wu Yunhua. Hopf bifurcation in the multi-dimension biomathematics model under small perturbation [J]. Acta mathematica scientia,Series A, 1999, 19(2): 187-195. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 127
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 80
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|