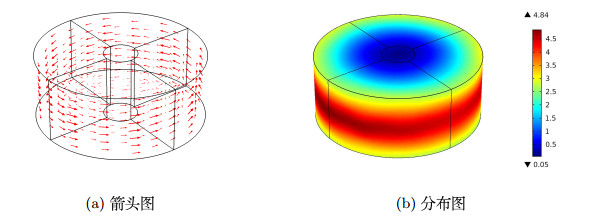
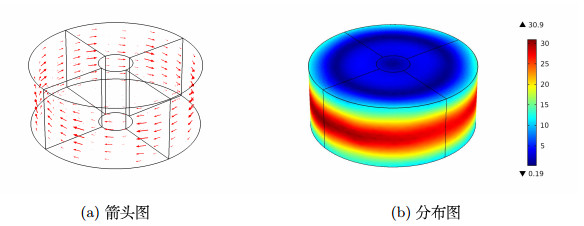
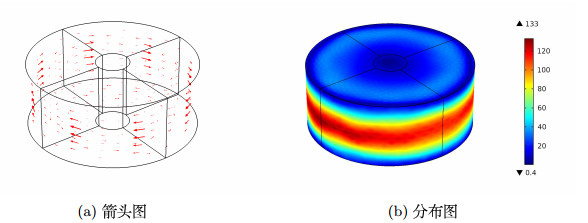
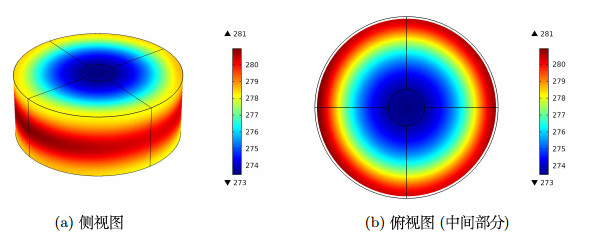
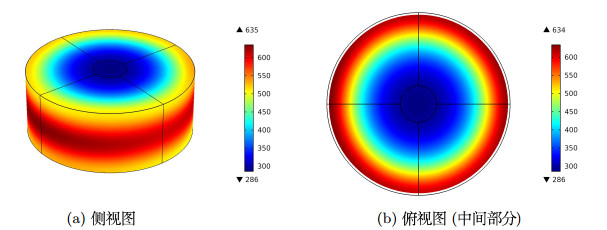
Acta mathematica scientia,Series A ›› 2022, Vol. 42 ›› Issue (4): 1238-1255.
Previous Articles Next Articles
Fully Discrete Finite Element Scheme for a Nonlinear Induction Heating Problem
Yuan Huang1,Yue Zhi3,Tong Kang1,2,Ran Wang1,2,*( ),Hong Zhang4
),Hong Zhang4
- 1 School of Data Science and Intelligent Media, Communication University of China, Beijing 100024
2 Key Laboratory of Computational Geodynamics, University of Chinese Academy of Sciences, Beijing 100049
3 Tongzhou Branch of Beijing Yucai School, Beijing 101101
4 Chaoyang Chuiyangliu Branch of Beijing Huiwen Middle School, Beijing 100021
-
Received:2021-03-30Online:2022-08-26Published:2022-08-08 -
Contact:Ran Wang E-mail:wangr@ucas.ac.cn -
Supported by:the National Key Research and Development Program of China(2020YFA0713401);the National Science Foundation of China(U2039207);the National Science Foundation of China(42074108);the National Science Foundation of China(41904067);the Fundamental Research Funds for the Central Universities
CLC Number:
- O241.82
Cite this article
Yuan Huang,Yue Zhi,Tong Kang,Ran Wang,Hong Zhang. Fully Discrete Finite Element Scheme for a Nonlinear Induction Heating Problem[J].Acta mathematica scientia,Series A, 2022, 42(4): 1238-1255.
share this article
| 1 |
Akrivis G , Larsson S . Linearly implicit finite element methods for the time dependent Joule heating problem. BIT Numerical Mathematics, 2005, 45: 429- 442
doi: 10.1007/s10543-005-0008-1 |
| 2 |
Barglik J , Doležel I , Karban P , et al. Modelling of continual induction hardening in quasi-coupled formulation. Compel-the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2005, 24 (1): 251- 260
doi: 10.1108/03321640510571273 |
| 3 |
Bermúdez A , Gómez D , Muniz M C , et al. Transient numerical simulation of a thermoelectrical problem in cylindrical induction heating furnaces. Advances in Computational Mathematics, 2007, 26: 39- 62
doi: 10.1007/s10444-005-7470-9 |
| 4 |
Bień M . Global solutions of the non-linear problem describing Joule's heating in three space dimensions. Mathematical Methods in the Applied Sciences, 2005, 28 (9): 1007- 1030
doi: 10.1002/mma.559 |
| 5 | Bossavit A , Emson C , Mayergoyz I D . Méthodes Numériques en Électromagnétisme. Paris: Eyrolles, 1991 |
| 6 |
Chovan J , Geuzaine C , Slodička M . \bmA-ϕ formulation of a mathematical model for the induction hardening process with a nonlinear law for the magnetic field. Computer Methods in Applied Mechanics and Engineering, 2017, 321: 294- 315
doi: 10.1016/j.cma.2017.03.045 |
| 7 | Elliott C M , Larsson S . A finite element model for the time-dependent Joule heating problem. Mathematics of Computation, 1995, 62 (212): 1433- 1453 |
| 8 | Evans L C. Graduate Studies in Mathematics: Partial Differential Equations. Second ed. New York: American Mathematical Society, 2010 |
| 9 |
Hömberg D . A mathematical model for induction hardening including mechanical effects. Nonlinear Analysis: Real World Applications, 2004, 5 (1): 55- 90
doi: 10.1016/S1468-1218(03)00017-8 |
| 10 | Hömberg D , Petzold T , Rocca E . Analysis and simulations of multifrequency induction hardening. Nonlinear Analysis: Real World Applications, 2005, 22: 84- 97 |
| 11 |
Kang T , Wang R , Zhang H . Potential field formulation based on decomposition of the electric field for a nonlinear induction hardening model. Communications in Applied Mathematics and Computational Science, 2019, 14 (2): 175- 205
doi: 10.2140/camcos.2019.14.175 |
| 12 |
Kang T , Wang R , Zhang H . Fully discrete \bmT-ψ finite element method to solve a nonlinear induction hardening problem. Numerical Methods for Partial Differential Equations, 2021, 37: 546- 582
doi: 10.1002/num.22540 |
| 13 | Nečas J . Introduction to the Theory of Nonlinear Elliptic Equations. Chichester: John Wiley & Sons Ltd, 1986 |
| 14 |
Nédélec J C . Mixed finite elements in R3. Numerische Mathematick, 1980, 35: 315- 341
doi: 10.1007/BF01396415 |
| 15 | Roubíček T . Nonlinear Partial Differential Equations with Applications. Berlin: Birkhöuser, 2005 |
| 16 |
Slodička M , Chovan J . Solvability for induction hardening including nonlinear magnetic field and controlled Joule heating. Applicable Analysis, 2017, 96: 2780- 2799
doi: 10.1080/00036811.2016.1243661 |
| 17 | Sun D , Manoranjan V S , Yin H M . Numerical solutions for a coupled parabolic equations arising induction heating processes. Conference Publications, 2007, 2007 (Special): 956- 964 |
| 18 | Vajnverg M . Variational Method and Method of Monotone Operators in the Theory of Nonlinear Equations. New York: John Wiley, 1973 |
| 19 |
Yin H M . On a nonlinear Maxwell's system in quasi-stationary electromagnetic fields. Mathematical Models and Methods in Applied Sciences, 2004, 14 (10): 1521- 1539
doi: 10.1142/S0218202504003787 |
| 20 |
Yin H M . Regularity of weak solution to Maxwell's equations and applications to microwave heating. Journal of Differential Equations, 2004, 200 (1): 137- 161
doi: 10.1016/j.jde.2004.01.010 |
| 21 |
Yin H M , Wei W . Regularity of weak solution for a coupled system arising from a microwave heating model. European Journal of Applied Mathematics, 2014, 25: 117- 131
doi: 10.1017/S0956792513000326 |
| [1] | Tingwei Pan,Suxiang He. The Greedy Simplex Algorithm for Double Sparsity Constrained Optimization Problems [J]. Acta mathematica scientia,Series A, 2022, 42(3): 920-933. |
| [2] | Ning-An LAI, Wei XIANG, Yi ZHOU. GLOBAL INSTABILITY OF MULTI-DIMENSIONAL PLANE SHOCKS FOR ISOTHERMAL FLOW [J]. Acta mathematica scientia,Series A, 2022, 42(3): 887-902. |
| [3] | Yingqiu LI, Xulan HUANG, Zhaohui PENG. CENTRAL LIMIT THEOREM AND CONVERGENCE RATES FOR A SUPERCRITICAL BRANCHING PROCESS WITH IMMIGRATION IN A RANDOM ENVIRONMENT [J]. Acta mathematica scientia,Series A, 2022, 42(3): 957-974. |
| [4] | Edcarlos D. SILVA, Jefferson S. SILVA. QUASILINEAR EQUATIONS USING A LINKING STRUCTURE WITH CRITICAL NONLINEARITIES [J]. Acta mathematica scientia,Series A, 2022, 42(3): 975-1002. |
| [5] | Changfeng Ma,Feiyang Ma. The Improved Convergence Theorems of Modulus-Based Matrix Splitting Iteration Methods for a Class of Nonlinear Complementarity Problems with H-Matrices [J]. Acta mathematica scientia,Series A, 2022, 42(2): 583-593. |
| [6] | Gonglin Yuan,Yulun Wu,Hongtruong Pham. A Modified HS-DY-Type Method with Nonmonotone Line Search for Image Restoration and Unconstrained Optimization Problems [J]. Acta mathematica scientia,Series A, 2022, 42(2): 605-620. |
| [7] | Hongwu Zhang. One Regularization Method for a Cauchy Problem of Semilinear Elliptic Equation [J]. Acta mathematica scientia,Series A, 2022, 42(1): 45-57. |
| [8] | Jing Zeng,Ruiting Hu. Stability of Benson Proper Efficient Solutions for Vector Optimization Problems [J]. Acta mathematica scientia,Series A, 2022, 42(1): 35-44. |
| [9] | Yuehong He,Xianjun Long. A Inertial Contraction and Projection Algorithm for Pseudomonotone Variational Inequality Problems [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1897-1911. |
| [10] | Zhibin Zhu,Yuanhang Geng. A Modified Three-Term WYL Conjugate Gradient Method [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1871-1879. |
| [11] | Xiaoxia Yang,Houchao Zhang. Discontinuous Galerkin Finite Element Analysis of for the Extended Fisher-Kolmogorov Equation [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1880-1896. |
| [12] | Zaiyun Zhang,Zhenhai Liu,Youjun Deng. Global Existence and General Decay for a Nonlinear Viscoelastic Equation with Time-Varying Delay and Velocity-Dependent Material Density [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1684-1704. |
| [13] | Cheng Ouyang,Jiaqi Mo. The Solitary Wave Solution to a Class of Nonlinear Dynamic System [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1830-1837. |
| [14] | Yuge Du,Shuying Tian. Existence and Blow-Up of a Parabolic Equation with Logarithmic Nonlinearity [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1816-1829. |
| [15] | Huaxin Chen,Wensheng Jia. Approximation Theorem and General Convergence of Population Games [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1566-1573. |
|