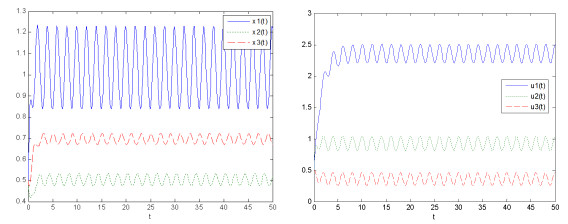
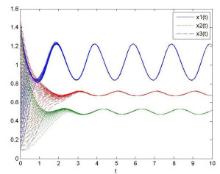
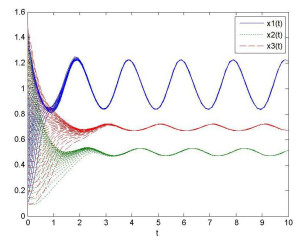
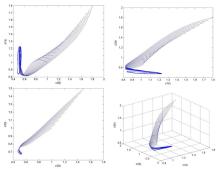
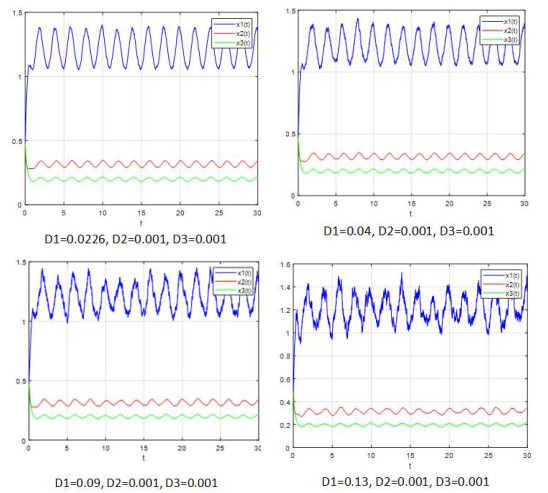
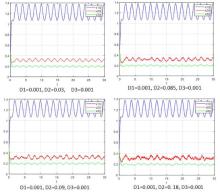
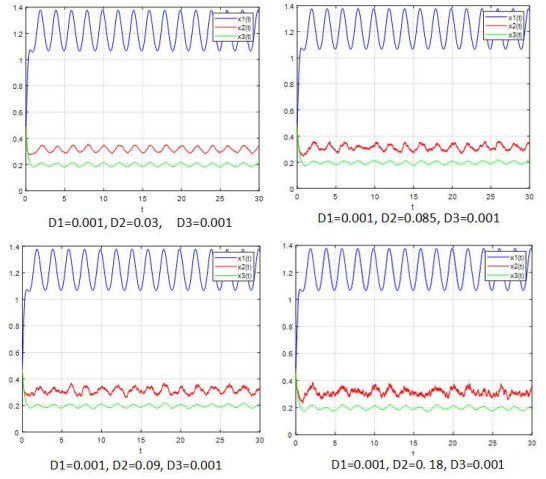
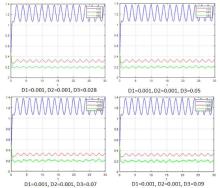
Acta mathematica scientia,Series A ›› 2022, Vol. 42 ›› Issue (1): 245-268.
Previous Articles Next Articles
On a Nonlinear Non-Autonomous Ratio-Dependent Food Chain Model with Delays and Feedback Controls
Changyou Wang1( ),Nan Li2,*(
),Nan Li2,*( ),Tao Jiang3,4,*(
),Tao Jiang3,4,*( ),Qiang Yang1
),Qiang Yang1
- 1 College of Applied Mathematics, Chengdu University of Information Technology, Chengdu 610225
2 Department of Applied Mathematics, Southwestern University of Finance and Economics, Chengdu 610074
3 Control Engineering College, Chengdu University of Information Technology, Chengdu 610225
4 State key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110169
-
Received:2020-09-26Online:2022-02-26Published:2022-02-23 -
Contact:Nan Li,Tao Jiang E-mail:wangchangyou417@163.com;2972028881@qq.com;jiangtop@126.com -
Supported by:the Robot Research Fund of State Key Laboratory(2019-O13);the Science Research Project of Sichuan Provincial Department(2021YFH0069);the Talent Introduction Project of Chengdu University of Information Engineering(KYTZ201820);the Sichuan Science and Technology Program(21ZYZYTS0158)
CLC Number:
- O175.12
Cite this article
Changyou Wang,Nan Li,Tao Jiang,Qiang Yang. On a Nonlinear Non-Autonomous Ratio-Dependent Food Chain Model with Delays and Feedback Controls[J].Acta mathematica scientia,Series A, 2022, 42(1): 245-268.
share this article
| 1 |
Arditi R , Ginzburg L R . Coupling in predator-prey dynamics: Ratio-dependence. Journal of Theoretical Biology, 1989, 139 (3): 311- 326
doi: 10.1016/S0022-5193(89)80211-5 |
| 2 | Basener W. Topology and Its Applications. Hoboken, NJ: John Wiley & Sons, 2006 |
| 3 |
Celik C . Stability and Hopf Bifurcation in a delayed ratio dependent Holling-Tanner type model. Applied Mathematics and Computation, 2015, 255: 228- 237
doi: 10.1016/j.amc.2014.11.086 |
| 4 |
Chen F . On a nonlinear nonautonomous predator-prey model with diffusion and distributed delay. Journal of Computational and Applied Mathematics, 2005, 180 (1): 33- 49
doi: 10.1016/j.cam.2004.10.001 |
| 5 |
Denaro G , Valenti D , La Cognata A , et al. Spatio-temporal behaviour of the deep chlorophyll maximum in Mediterranean Sea: Development of a stochastic model for picophytoplankton dynamics. Ecological Complexity, 2013, 13: 21- 34
doi: 10.1016/j.ecocom.2012.10.002 |
| 6 |
Ding W , Huang W Z . Global dynamics of a ratio-dependent holling-tanner predator-prey system. Journal of Mathematical Analysis and Applications, 2018, 460 (1): 458- 475
doi: 10.1016/j.jmaa.2017.11.057 |
| 7 |
Dubkov A A , Spagnolo B . Verhulst model with lévy white noise excitation. The European Physical Journal B, 2008, 65 (3): 361- 367
doi: 10.1140/epjb/e2008-00337-0 |
| 8 | Falci G, La Cognata A, Berritta M, et al. Design of a lambda system for population transfer in superconducting nanocircuits. Physical Review B, 2013, 87, ID: 214515 |
| 9 | Feistel R, Ebeling W. Evolution of Complex System. Dordrecht: Kluwer, 1989 |
| 10 | Freeze M , Chang Y , Feng W . Analysis of dynamics in a complex food chain with ratio-dependent functional response. Journal of Applied Analysis & Computation, 2014, 4 (1): 69- 87 |
| 11 |
Garay J , Cressman R , Xu F , et al. Optimal forager against ideal free distributed prey. The American Naturalist, 2015, 186 (1): 111- 122
doi: 10.1086/681638 |
| 12 |
Giuffrida A , Valenti D , Ziino G , et al. A stochastic interspecific competition model to predict the behaviour of Listeria monocytogenes in the fermentation process of a traditional Sicilian salami. European Food Research and Technology, 2009, 228 (5): 767- 775
doi: 10.1007/s00217-008-0988-6 |
| 13 | Gopalsamy K , Weng P . Global attractivity in a competition system with feedback controls. Computers and Mathematics with Applications, 2003, 45 (4/5): 665- 676 |
| 14 | Haken H . Advanced Synergetics. Berlin: Springer, 1985 |
| 15 | Horsthemke W , Lefever R . Noise-Induced Transitions. Theory and Applications in Physics. Chemistry, and Biology. Berlin: Springer, 1984 |
| 16 | Khalil H K. Nonlinear Systems. Englewood Cliffs: Prentice-Hall, 2002 |
| 17 | Liang Z Q , Pan H W . Qualitative analysis of a ratio-dependent holling-tanner model. Journal of Mathematical Analysis & Applications, 2007, 334 (2): 954- 964 |
| 18 |
Liang Z Q , Zeng X P , Pang G P , Liang Y H . Periodic solution of a leslie predator-prey system with ratio-dependent and state impulsive feedback control. Nonlinear Dynamics, 2017, 89 (4): 2941- 2955
doi: 10.1007/s11071-017-3637-4 |
| 19 | Louartassi Y , Alla A , Hattaf K , Nabil A . Dynamics of a predator-prey model with harvesting and reserve area for prey in the presence of competition and toxicity. Journal of Applied Mathematics and Computing, 2019, 59 (1/2): 305- 321 |
| 20 |
Lu G , Lu Z , Lian X . Delay effect on the permanence for lotka-volterra cooperative systems. Nonlinear Analysis: Real World Applications, 2010, 11 (4): 2810- 2816
doi: 10.1016/j.nonrwa.2009.10.005 |
| 21 |
Mikhaylov A N , Gryaznov E G , Belov A L , et al. Field- and irradiation-induced phenomena in memristive nanomaterials. Physica Status Solidi (c), 2016, 13: 870- 881
doi: 10.1002/pssc.201600083 |
| 22 |
Muhammadhaji A , Teng Z , Rehim M . Dynamical behavior for a class of delayed competitive-mutualism systems. Differential Equations and Dynamical Systems, 2015, 23 (3): 281- 301
doi: 10.1007/s12591-014-0226-6 |
| 23 |
Nakata Y , Muroya Y . Permanence for nonautonomous Lotka-Volterra cooperative systems with delays. Nonlinear Analysis: Real World Applications, 2010, 11 (1): 528- 534
doi: 10.1016/j.nonrwa.2009.01.002 |
| 24 | Nicolis G , Prigogine L . Self-Organization in Non-Equilibrium Systems. New Jersey: Wiley, 1977 |
| 25 | Nie L , Teng Z , Hu L , Peng J G . Permanence and stability in non-autonomous predator-prey Lotka-Volterra systems with feedback controls. Computers & Mathematics with Applications, 2009, 58 (3): 436- 448 |
| 26 |
Shen C X , You M S . Permanence and extinction of a three-species ratio-dependent food chain model with delay and prey diffusion. Applied Mathematics and Computation, 2010, 217 (5): 1825- 1830
doi: 10.1016/j.amc.2010.02.037 |
| 27 | Spagnolo B , La Barbera A . Role of the noise on the transient dynamics of an ecosystem of interacting species. Physica A: Statistical Mechanics and its Applications, 2002, 315 (1/2): 114- 124 |
| 28 | Spagnolo B , Dubkov A A , Pankratov A L , et al. Lifetime of metastable states and suppression of noise in interdisciplinary physical models. Acta Physica Polonica B, 2007, 38 (5): 1925- 1950 |
| 29 |
Spagnolo B , Valenti D . Volatility effects on the escape time in financial market models. International Journal of Bifurcation and Chaos, 2008, 18 (9): 2775- 2786
doi: 10.1142/S0218127408022007 |
| 30 | Valenti D , Schimansky-Geier L , Sailer X , Spagnolo B . Moment equations for a spatially extended system of two competing species. The European Physical Journal B, 2006, 50 (1/2): 199- 203 |
| 31 | Wang C Y , Li N , Zhou Y , Pu X , Li R . On a multi-delay lotka-volterra predator-prey model with feedback controls and prey diffusion. Acta Mathematica Scientia, 2019, 39B (2): 429- 448 |
| 32 | Wang C Y, Zhou Y Q, Li Y H, Li R. Well-posedness of a ratio-dependent lotka-volterra system with feedback control. Boundary Value Problems, 2018, 2018, ID: 117 |
| 33 |
Xu F , Cressman R , Křivan V . Evolution of mobility in predator-prey systems. Discrete and Continuous Dynamical Systems-Series B, 2014, 19 (10): 3397- 3432
doi: 10.3934/dcdsb.2014.19.3397 |
| 34 | Xu J, Chen F. Permanence of a Lotka-Volterra cooperative system with time delays and feedback controls. Communications in Mathematical Biology & Neuroscience, 2015, 2015, ID: 18 |
| 35 | Xu R , Chaplain M . Persistence and global stability in a delayed predator-prey system with michaelis-menten type functional response. Applied Mathematics and Computation, 2002, 130 (1): 441- 455 |
| 36 |
Xu R , Chen L S . Ersistence and global stability for a delayed nonautonomous predator-prey system without dominating instantaneous negative feedback. Journal of Mathematical Analysis and Applications, 2001, 262 (1): 50- 61
doi: 10.1006/jmaa.2001.7524 |
| 37 |
Zhou J , Mu C . Coexistence of a diffusive predator-prey model with holling type-Ⅱ functional response and density dependent mortality. Journal of Mathematical Analysis and Applications, 2012, 385 (2): 913- 927
doi: 10.1016/j.jmaa.2011.07.027 |
| 38 | Zhang Q M, Zhang X J, Yang H F. Global dissipativity of stochastic Lotka-Volterra system with feedback controls. International Journal of Biomathematics, 2017, 10(2), ID: 1750022 |
| [1] | Zhu Kaixuan, Xie Yongqin, Mei Xinyu, Deng Xijun. Uniform Attractors for the Sup-Cubic Weakly Damped Wave Equations with Delays [J]. Acta mathematica scientia,Series A, 2022, 42(1): 86-102. |
| [2] | Chenyang Xia,Zhenhui Wang,Zhibo Cheng. Positive Periodic Solutions for a Damped Duffing Equation with Singularity of Attractive Type [J]. Acta mathematica scientia,Series A, 2022, 42(1): 131-138. |
| [3] | Yue Sun,Daoxiang Zhang,Wen Zhou. The Influence of Fear Effect on Stability Interval of Reaction-Diffusion Predator-Prey System with Time Delay [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1980-1992. |
| [4] | Zaiyun Zhang,Zhenhai Liu,Youjun Deng. Global Existence and General Decay for a Nonlinear Viscoelastic Equation with Time-Varying Delay and Velocity-Dependent Material Density [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1684-1704. |
| [5] | Zhiyu Zhang,Cheng Zhao,Yuyu Li. Oscillation of Second Order Delay Dynamic Equations with Superlinear Neutral Terms on Time Scales [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1838-1852. |
| [6] | Guijiang Qin,Jiashan Yang. Oscillation Theorems of Second-Order Variable Delay Dynamic Equations with Quasilinear Neutral Term [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1492-1503. |
| [7] | Jing Yang,Changcheng Ke,Zhouchao Wei. Study on Periodic Solutions of a Class of Continuous and Discontinuous Piece-Wise Linear Systems [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1053-1065. |
| [8] | Jingnan Wang,Dezhong Yang. Stability and Bifurcation of a Pathogen-Immune Model with Delay and Diffusion Effects [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1204-1217. |
| [9] | Qingye Zhang,Bin Xu. Multiple Periodic Solutions for a Class of Stationary Dirac Equations with Local Nonlinearity [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1013-1023. |
| [10] | Shiping Lu,Shile Zhou,Xingchen Yu. Periodic Solutions for a Singular Liénard Equation with Sign-Changing Weight Functions [J]. Acta mathematica scientia,Series A, 2021, 41(3): 686-701. |
| [11] | Zhiyu Zhang. Oscillation Criteria of Second-Order Generalized Emden-Fowler Delay Differential Equations with a Sub-Linear Neutral Term [J]. Acta mathematica scientia,Series A, 2021, 41(3): 811-826. |
| [12] | Xiling Li,Fei Gao,Wenqin Li. Stability Analysis of Fractional-Order Hepatitis B Virus Infection Model With Immune Delay [J]. Acta mathematica scientia,Series A, 2021, 41(2): 562-576. |
| [13] | Tingting Jiang,Zengji Du. Periodic Solutions of a Neutral Impulsive Predator-Prey Model with Holling-Type IV Functional Response [J]. Acta mathematica scientia,Series A, 2021, 41(1): 178-193. |
| [14] | Kaixuan Zhu,Yongqin Xie,Feng Zhou,Xijun Deng. Pullback Attractors for the Complex Ginzburg-Landau Equations with Delays [J]. Acta mathematica scientia,Series A, 2020, 40(5): 1341-1353. |
| [15] | Jian Liu,Zhixin Zhang,Wei Jiang. Global Mittag-Leffler Stability of Fractional Order Nonlinear Impulsive Differential Systems with Time Delay [J]. Acta mathematica scientia,Series A, 2020, 40(4): 1053-1060. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 150
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 160
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|