物理信息神经网络求解五阶 emKdV 方程的正反问题

摘要/Abstract

摘要：

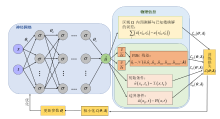
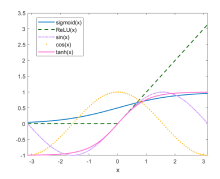
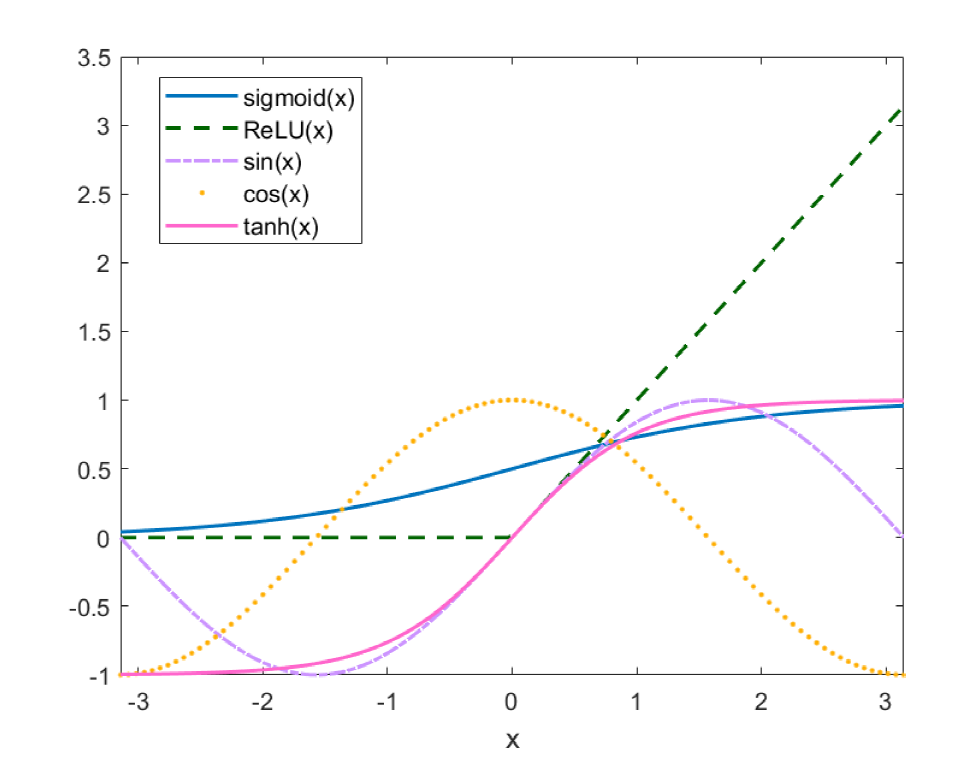
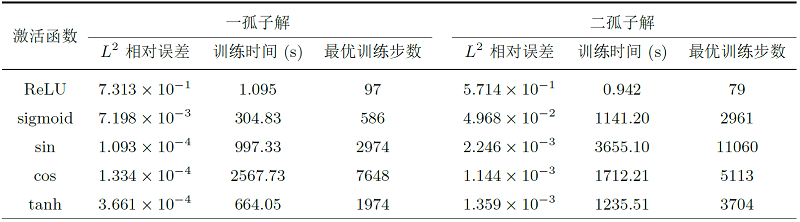
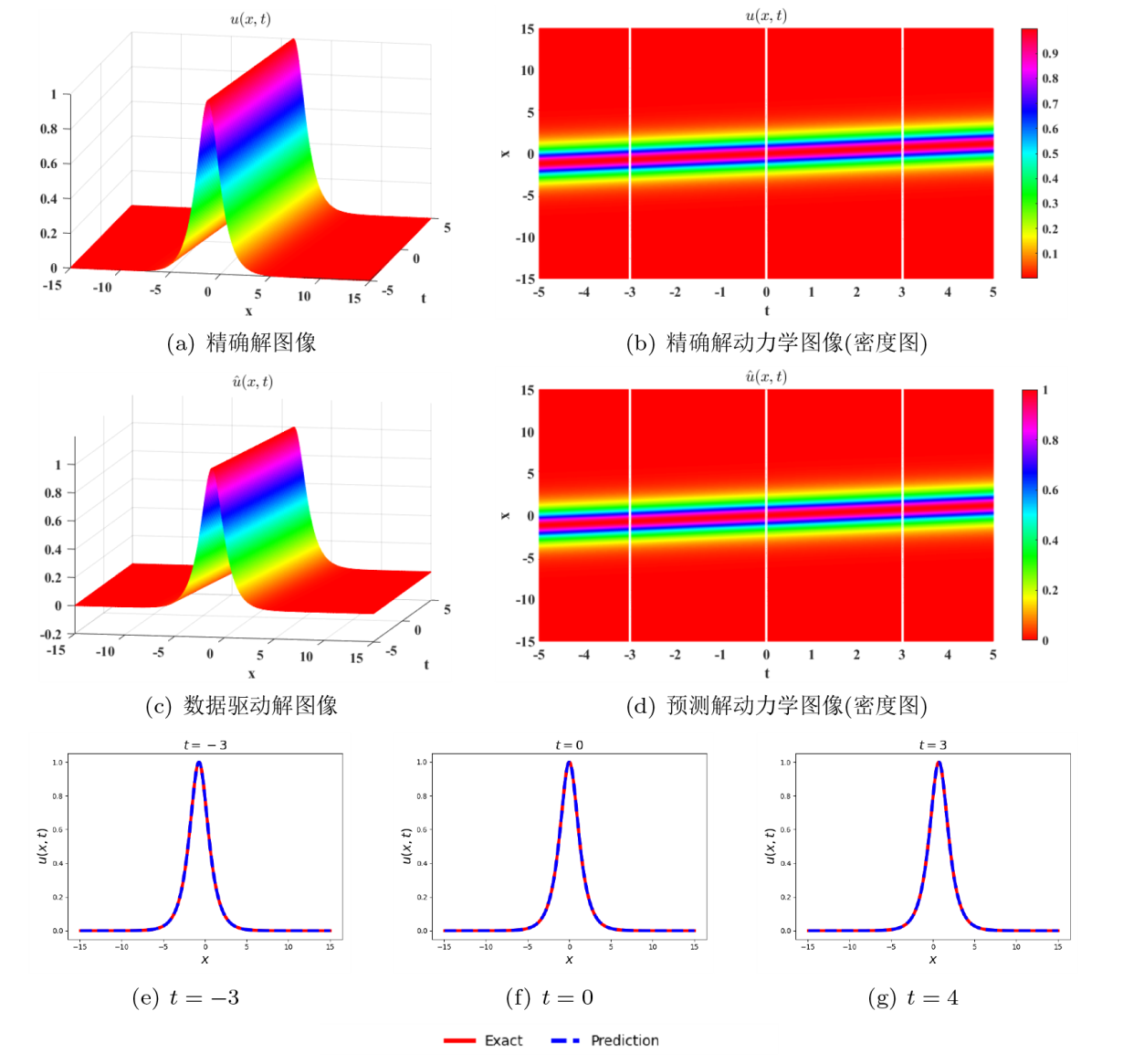
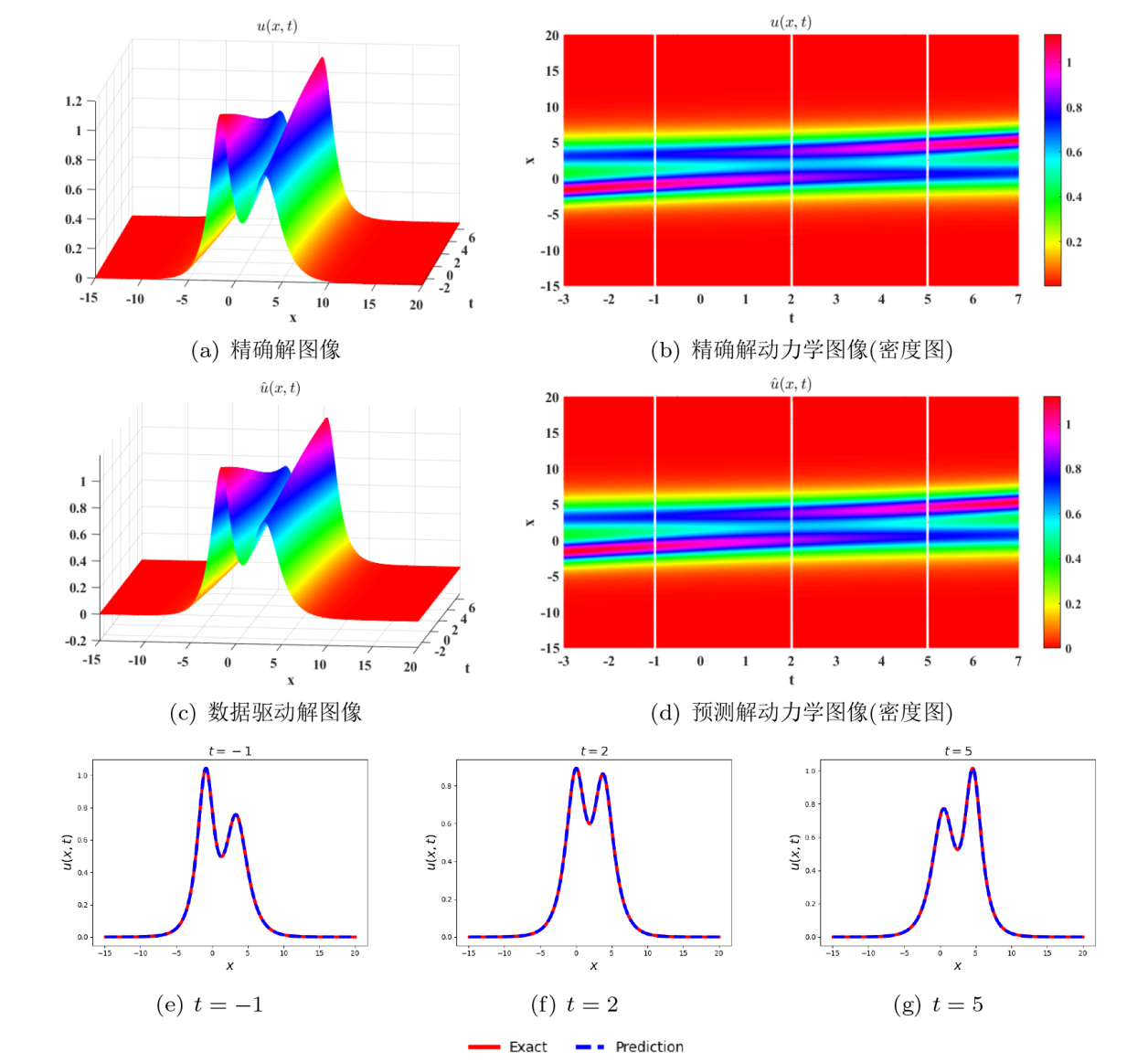
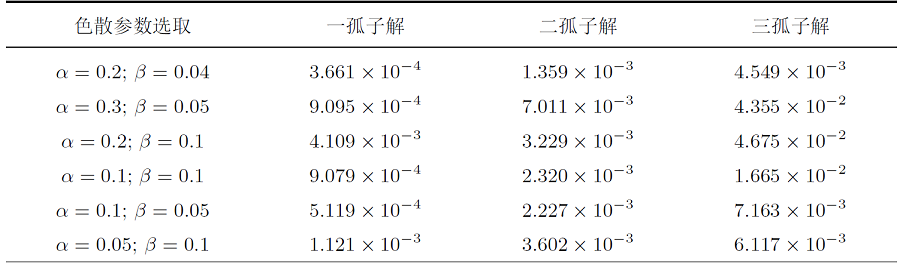
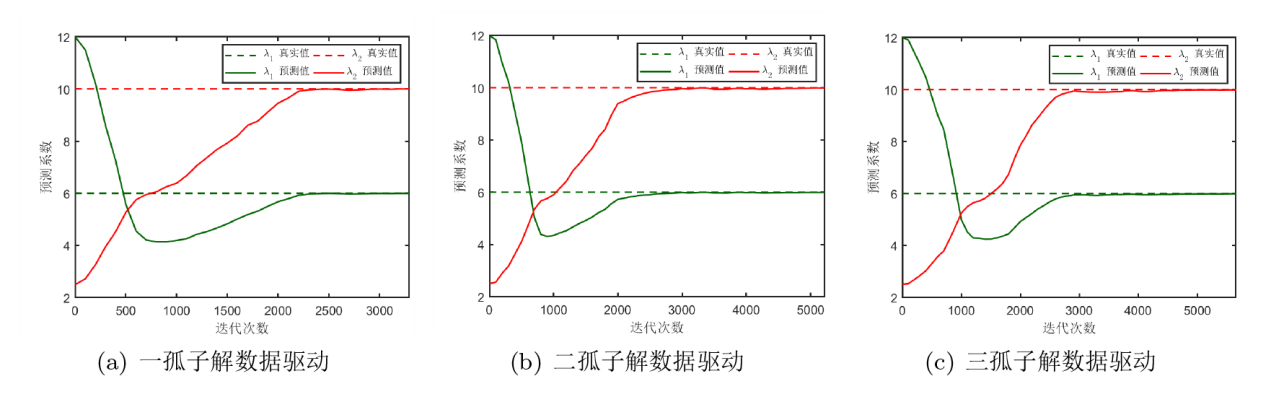
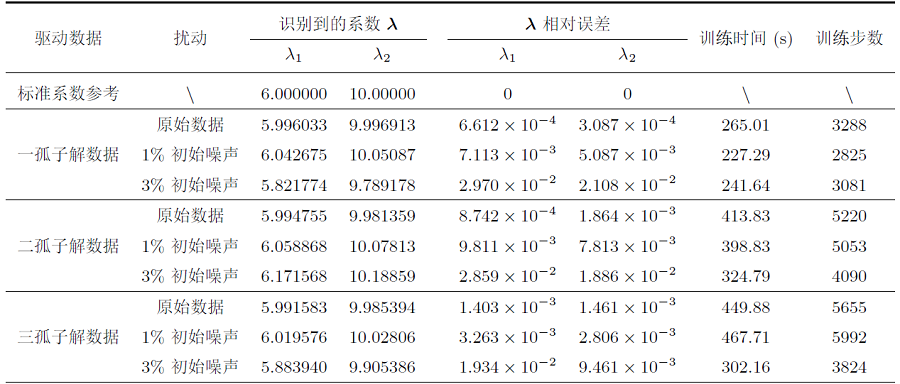
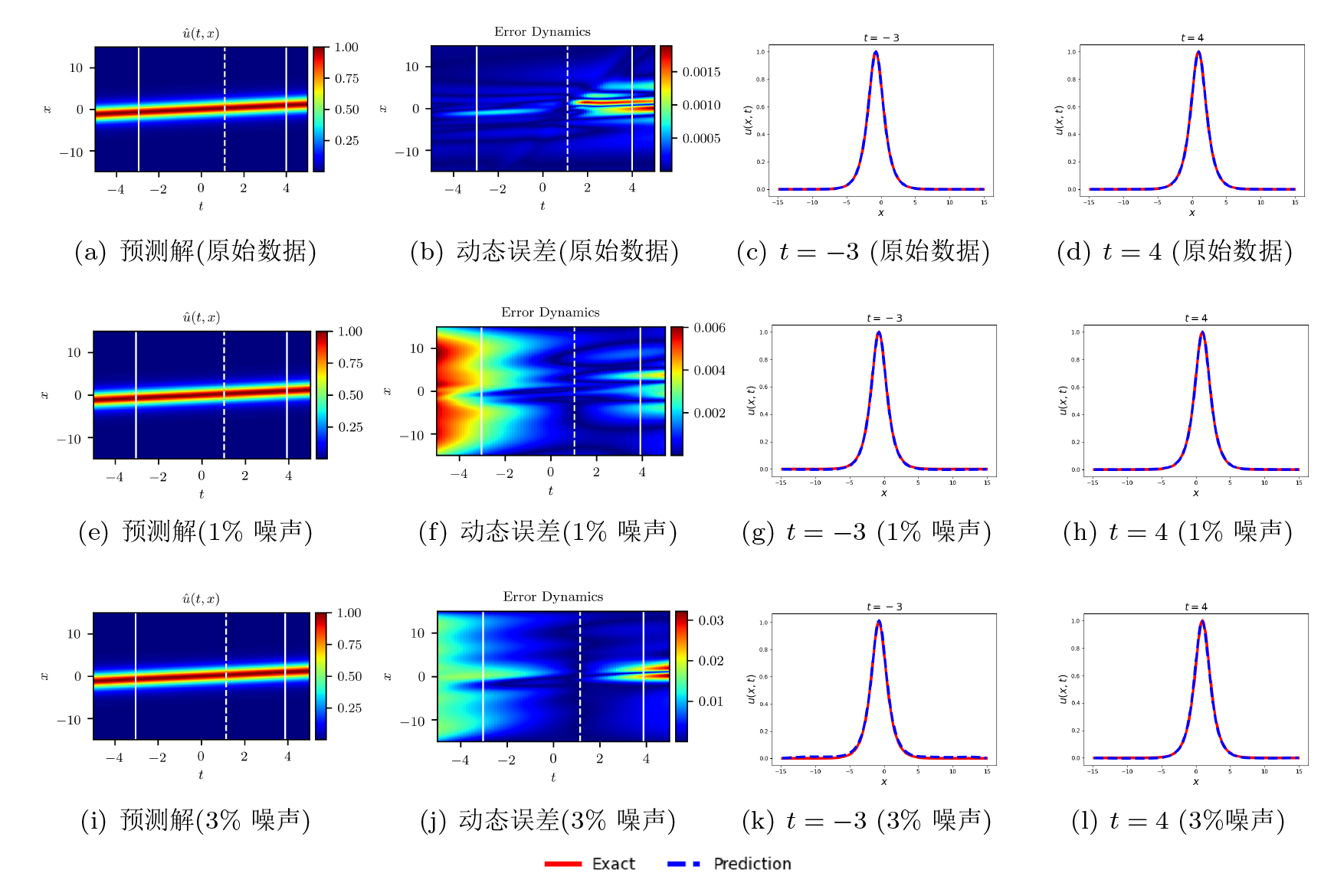
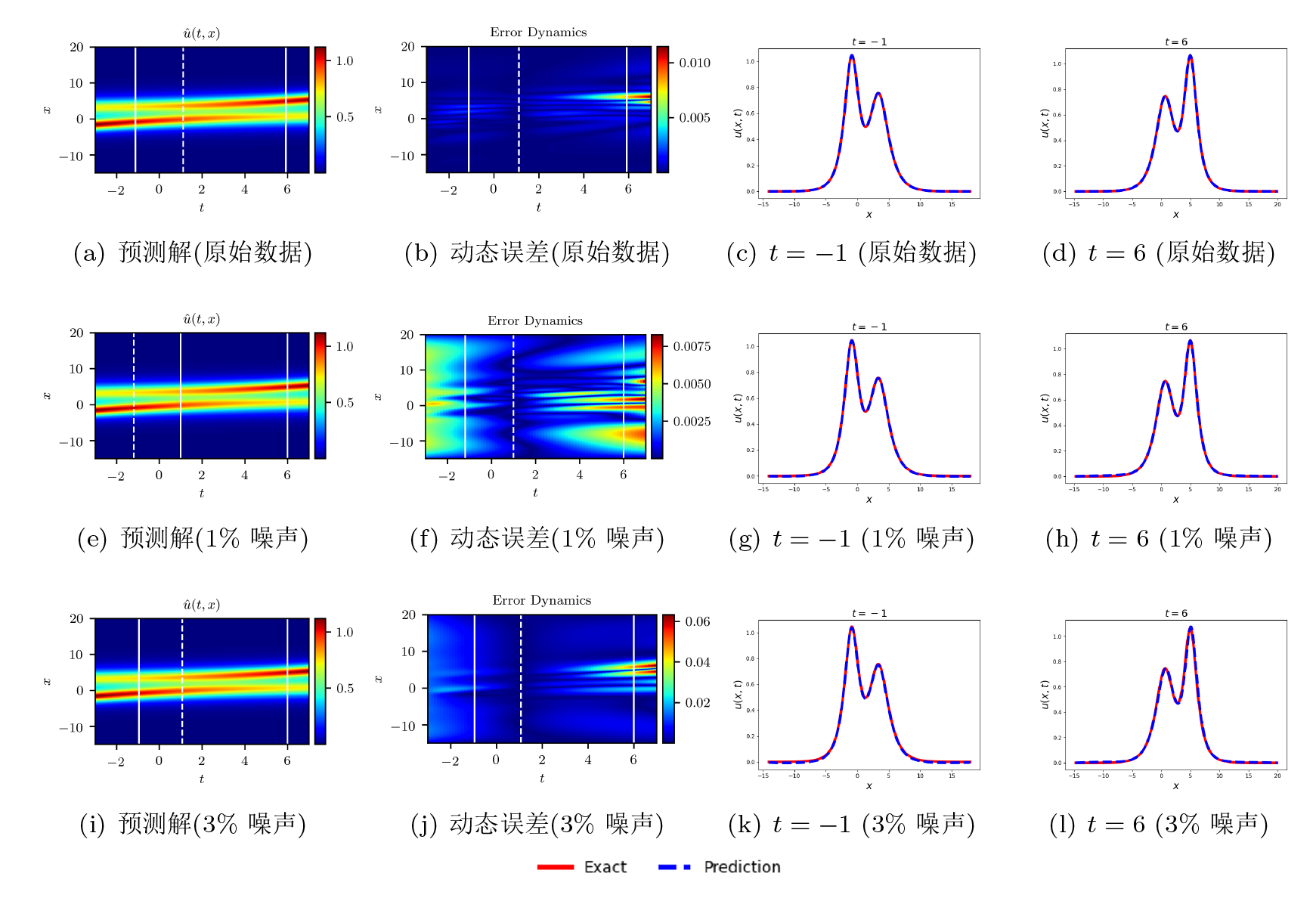
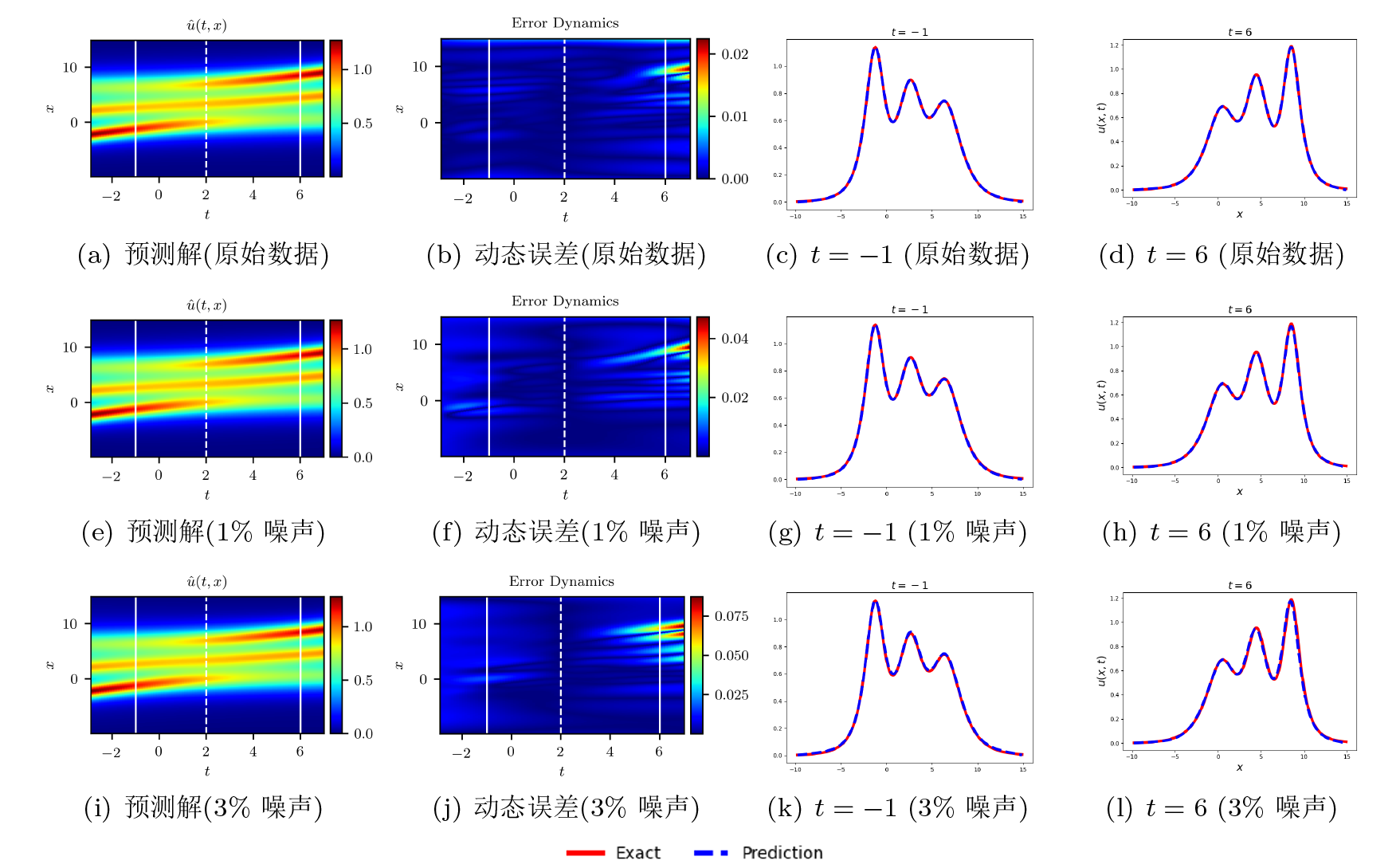
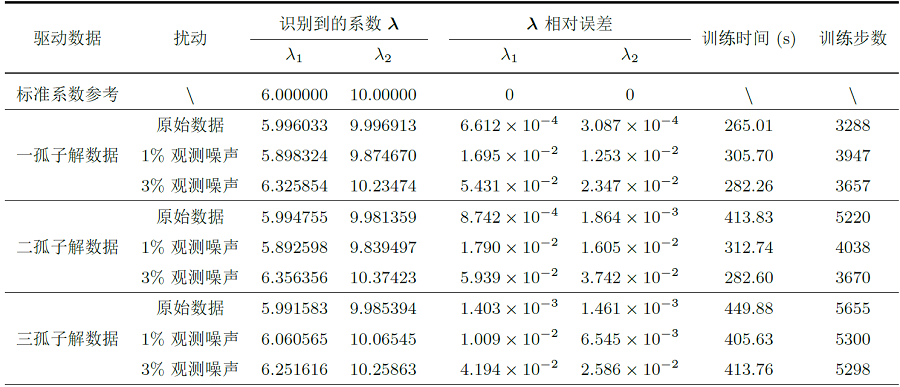
该文利用物理信息神经网络 (PINNs) 对扩展的五阶 mKdV (emKdV) 方程的正反问题进行求解, 并对孤子的动力学行为进行分析、模拟. 针对正问题, 选用双曲正切函数 $\tanh$ 作为激活函数求解方程的一、二、三孤子解, 并将 PINNs 方法求得的数据驱动解与借助简化的 Hirota 方法给出的方程精确解进行比较, 一孤子解的精度为 $\mathcal{O}(10^{-4})$, 二、三孤子解的精度为 $\mathcal{O}(10^{-3})$. 针对反问题, 分别由一、二、三孤子解的数据进行驱动求解方程的两个待定系数, 并在不同的噪声下探究算法的鲁棒性. 当在训练数据中加入 1% 的初始噪声或观测噪声时, 待求系数的预测精度可分别达到 $\mathcal{O}(10^{-3})$ 和 $\mathcal{O}(10^{-2})$; 当加入 3% 的初始噪声或观测噪声时, 预测精度依然可以达到 $\mathcal{O}(10^{-2})$; 由实验数据分析可知观测噪声对 PINNs 模型的影响要略大于初始噪声.

关键词: 物理信息神经网络, 五阶 emKdV 方程, 数据驱动解, 非线性动力学

Abstract:

With the help of the physics-informed neural networks (PINNs), the forward and inverse problems of extended fifth-order mKdV(emKdV) equation are tackled, and the dynamic behaviors of solitons are also analyzed and simulated in this paper. The hyperbolic tangent function $\tanh$ is selected as the activation function to solve the one, two and three-soliton solutions of the equation. Moreover, the data-driven solutions obtained by PINNs method are compared with the exact solution given by the simplified Hirota method. Specifically, the accuracy of one-soliton solution is $\mathcal{O}(10^{-4})$, and the accuracy of the two-soliton and three-soliton solutions is $\mathcal{O}(10^{-3})$. For the inverse problem, the coefficients of the equation are discovered by the data of one, two and three-soliton solutions, respectively. Meanwhile, the robustness of the PINNs algorithm is explored under different noises. The accuracy of the data-driven coefficients can reach $\mathcal{O}(10^{-3})$ or $\mathcal{O}(10^{-2})$ respectively, when 1% initial noise or observation noise is added to the training data. And the prediction accuracy can still reach $\mathcal{O}(10^{-2})$ even if 3% initial noise or observation noise is added. According to the analysis of experimental data, the impact of observation noise on PINNs model is slightly greater than the initial noise.

Key words: Physics-informed neural networks, Fifth-order emKdV equations, Data-driven solutions, Nonlinear dynamics

中图分类号:

O241.8

吴泽康, 王晓丽, 韩文静, 李金红. 物理信息神经网络求解五阶 emKdV 方程的正反问题[J]. 数学物理学报, 2024, 44(2): 484-499.

Wu Zekang, Wang Xiaoli, Han Wenjing, Li Jinhong. Solving the Forward and Inverse Problems of Extended Fifth-Order mKdV Equation Via Physics-Informed Neural Networks[J]. Acta mathematica scientia,Series A, 2024, 44(2): 484-499.

图/表 15

图 1

图 2

图 3

表 1

图 4

图 5

图 6

表 2

表 3

图 7

表 4

图 8

图 9

图 10

表 5

参考文献 33

[1]	Draper L. Freak wave. Mar Obs, 1965, 35(2): 193-195
[2]	Haus H A, Wong W S. Solitons in optical communications. Rev Mod Phys, 1996, 68(2): 423-444 doi: 10.1103/RevModPhys.68.423
[3]	Zabusky N J, Kruskal M D. Interaction of "solitons" in a collisionless plasma and the recurrence of initial states. Phys Rev Lett, 1965, 15(6): 240-243 doi: 10.1103/PhysRevLett.15.240
[4]	Parkins A S, Walls D F. The physics of trapped dilute-gas Bose-Einstein condensates. Phys Rep, 1998, 303(1): 1-80 doi: 10.1016/S0370-1573(98)00014-3
[5]	Wadati M. The modified Korteweg-de Vries equation. J Phys Soc Jpn, 1973, 34(5): 1289-1296 doi: 10.1143/JPSJ.34.1289
[6]	黄念宁. 孤子理论和微扰方法. 上海: 上海科技教育出版社, 1996
	Huang N N. Theory of Solitons and Method of Pertubations. Shanghai: Shanghai Scientific and Technological Education Press, 1996
[7]	Leblond H, Grelu P, Mihalache D. Models for supercontinuum generation beyond the slowly-varying-envelope approximation. Phys Rev A, 2014, 90(5): 053816 doi: 10.1103/PhysRevA.90.053816
[8]	Ono H. Soliton fission in anharmonic lattices with reflectionless inhomogeneity. J Phys Soc Jpn, 1992, 61(12): 4336-4343 doi: 10.1143/JPSJ.61.4336
[9]	Khater A H, El-Kalaawy O H, Callebaut D K. Bäcklund transformations and exact solutions for Alfvén solitons in a relativistic electron-positron plasma. Phys Scr, 1998, 58(6): 545 doi: 10.1088/0031-8949/58/6/001
[10]	Ito M. An extension of nonlinear evolution equations of the KdV (mKdV) type to higher orders. J Phys Soc Jpn, 1980, 49(2): 771-778 doi: 10.1143/JPSJ.49.771
[11]	Marchant T R, Smyth N F. Soliton interaction for the extended Korteweg-de Vries equation. IMA J Appl Math, 1996, 56(2): 157-176 doi: 10.1093/imamat/56.2.157
[12]	Marchant T R, Smyth N F. The extended Korteweg-de Vries equation and the resonant flow of a fluid over topography. J Fluid Mech, 1990, 221: 263-287
[13]	Wazwaz A M, Xu G Q. An extended modified KdV equation and its Painlevé integrability. Nonlinear Dyn, 2016, 86: 1455-1460
[14]	GrimShaw R, PelinovSky E, Poloukhina O. Higher-order Korteweg-de Vries models for internal solitary waves in a stratified shear flow with a free surface. Nonlin Processes Geophys, 2002, 9(3/4): 221-235 doi: 10.5194/npg-9-221-2002
[15]	Pelinovskii E N, Polukhina O E, Lamb K. Nonlinear internal waves in the ocean stratified in density and current. Oceanology, 2000, 40(6): 757-766
[16]	Wang X, Zhang J L, Wang L. Conservation laws, periodic and rational solutions for an extended modified Korteweg-de Vries equation. Nonlinear Dyn, 2018, 92: 1507-1516
[17]	Liu N, Guo B L, Wang D S, et al. Long-time asymptotic behavior for an extended modified Korteweg-de Vries equation. Commun Math Sci, 2019, 17(7): 1877-1913 doi: 10.4310/CMS.2019.v17.n7.a6
[18]	Baydin A G, Pearlmutter B A, Radul A A, et al. Automatic differentiation in machine learning: a survey. J March Learn Res, 2018, 18: 1-43
[19]	Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys, 2019, 378: 686-707
[20]	Li J, Chen Y. Solving second-order nonlinear evolution partial differential equations using deep learning. Commun Theor Phys, 2020, 72(10): 105005 doi: 10.1088/1572-9494/aba243
[21]	Li J, Chen Y. A deep learning method for solving third-order nonlinear evolution equations. Commun Theor Phys, 2020, 72(11): 115003 doi: 10.1088/1572-9494/abb7c8
[22]	Li J H, Chen J C, Li B. Gradient-optimized physics-informed neural networks (GOPINNs): a deep learning method for solving the complex modified KdV equation. Nonlinear Dyn, 2022, 107: 781-792
[23]	田十方, 李彪. 梯度优化物理信息神经网络 (GOPINNs): 求解复杂非线性问题的深度学习方法. 物理学报, 2023, 72(10): 100202 doi: 10.7498/aps.72.20222381
	Tian S F, Li B. Gradient-optimized physics-informed neural networks (GOPINNs): a deep learning method for solving complex nonlinear problems. Acta Phys Sin, 2023, 72(10): 100202 doi: 10.7498/aps.72.20222381
[24]	Wang L, Yan Z Y. Data-driven rogue waves and parameter discovery in the defocusing nonlinear Schrödinger equation with a potential using the PINN deep learning. Phys Lett A, 2021, 404: 127408 doi: 10.1016/j.physleta.2021.127408
[25]	Cui S K, Wang Z, Han J Q, et al. A deep learning method for solving high-order nonlinear soliton equations. Commun Theor Phys, 2022, 74(7): 075007 doi: 10.1088/1572-9494/ac7202
[26]	Li J H, Li B. Mix-training physics-informed neural networks for the rogue waves of nonlinear Schrödinger equation. Chaos, Solitons & Fractals, 2022, 164: 112712 doi: 10.1016/j.chaos.2022.112712
[27]	Jin P Z, Lu L, Tang Y F, et al. Quantifying the generalization error in deep learning in terms of data distribution and neural network smoothness. Neural Networks, 2020, 130: 85-99
[28]	Lu L, Meng X H, Mao Z P, et al. DeepXDE: A deep learning library for solving differential equations. SIAM Rev, 2021, 63: 208-228
[29]	Wang S F, Yu X L, Perdikaris P. When and why PINNs fail to train: A neural tangent kernel perspective. J Comput Phys, 2022, 449: 110768 doi: 10.1016/j.jcp.2021.110768
[30]	Son H, Jang J W, Han W J, et al. Sobolev training for physics informed neural networks. arXiv proprint arXiv: 2101. 08932.2021
[31]	Liu D C, Nocedal J. On the limited memory BFGS method for large scale optimization. Math Program, 1989, 45(1): 503-528 doi: 10.1007/BF01589116
[32]	Stein M. Large sample properties of simulations using Latin hypercube sampling. Technometrics, 1987, 29(2): 143-151 doi: 10.1080/00401706.1987.10488205
[33]	Jiao Y L, Lai Y M, Li D W, et al. A rate of convergence of physics informed neural networks for the linear second order elliptic pdes. Commun Comput Phys, 2022, 31(4): 1272-1295 doi: 10.4208/cicp