周期边界条件下四阶特征值问题的一种有效的 Fourier 谱逼近

数学物理学报 ›› 2024, Vol. 44 ›› Issue (1): 37-49.

周期边界条件下四阶特征值问题的一种有效的 Fourier 谱逼近

何娅(),安静^*()

贵州师范大学数学科学学院贵阳 550025

收稿日期:2022-09-06 修回日期:2023-08-25 出版日期:2024-02-26 发布日期:2024-01-10
通讯作者: 安静, E-mail:aj154@163.com
作者简介:何娅, E-mail:Hy10190726@163.com
基金资助:
国家自然科学基金项目(12061023);贵州省科技计划项目(黔科合平台人才[2017]5726-39);贵州师范大学学术新苗基金项目(黔师新苗[2021]A04)

An Effective Fourier Spectral Approximation for Fourth-Order Eigenvalue Problems with Periodic Boundary Conditions

He Ya(),An Jing()

School of Mathematical Sciences, Guizhou Normal University, Guiyang 550025

Received:2022-09-06 Revised:2023-08-25 Online:2024-02-26 Published:2024-01-10
Supported by:
National Natural Science Foundation of China(12061023);Guizhou Province Science and Technology Planning Project(Guizhou Science);Guizhou Province Science and Technology Planning Project(Technology Cooperation Platform Talents [2017]5726-39);Guizhou Normal University Academic New Talent Foundation(Qian Teacher New Talent [2021]A04)

摘要/Abstract

摘要：

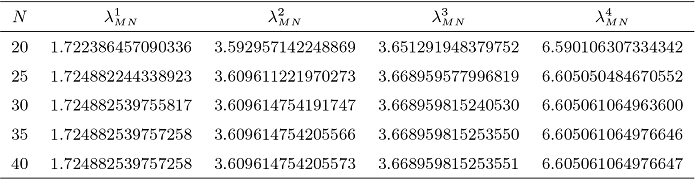
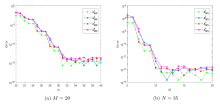
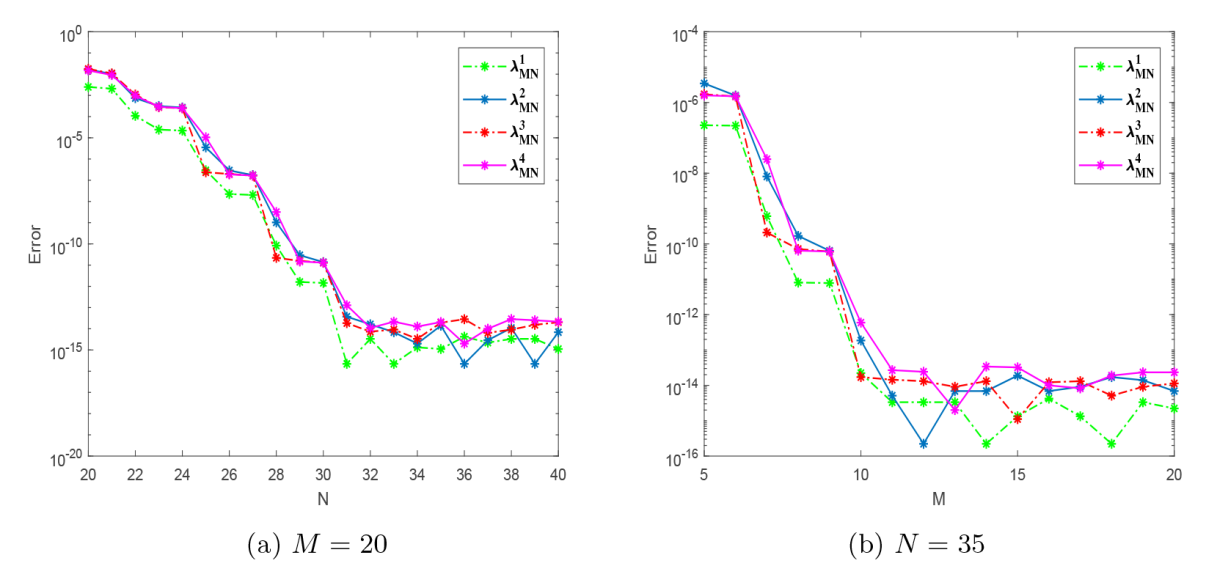
文章提出了周期边界条件下四阶特征值问题的一种有效的 Fourier 谱逼近方法. 首先, 根据周期边界条件引入了适当的 Sobolev 空间和相应的逼近空间, 建立了原问题的一种弱形式及其离散格式, 并推导了等价的算子形式. 其次, 定义了正交投影算子, 并证明了其逼近性质, 结合紧算子的谱理论证明了逼近特征值的误差估计. 另外, 构造了逼近空间中的一组基函数, 推导了离散格式基于张量积的矩阵形式. 最后, 文章给出了一些数值算例, 数值结果表明其算法是有效的和谱精度的.

关键词: 周期边界, 四阶特征值问题, Fourier 谱方法, 误差估计

Abstract:

In this paper, we put forward an effective Fourier spectral approximation method for fourth-order eigenvalue problems with periodic boundary conditions. Firstly, we introduce the appropriate Sobolev space and the corresponding approximation space according to the periodic boundary conditions, establish a weak form of the original problem and its discrete form, and derive the equivalent operator form. Then we define an orthogonal projection operator and prove its approximation properties. Combined with the spectral theory of compact operators, we prove the error estimates of approximation eigenvalues. In addition, we construct a set of basis functions of the approximation space, and derive the matrix form based on tensor product associated with the discrete scheme. Finally, we provide some numerical examples, and the numerical results show our algorithm is effective and spectral accuracy.

Key words: Periodic boundary, Fourth-order eigenvalue problem, Fourier spectral method, Error estimates

中图分类号:

O241.82

何娅, 安静. 周期边界条件下四阶特征值问题的一种有效的 Fourier 谱逼近[J]. 数学物理学报, 2024, 44(1): 37-49.

He Ya, An Jing. An Effective Fourier Spectral Approximation for Fourth-Order Eigenvalue Problems with Periodic Boundary Conditions[J]. Acta mathematica scientia,Series A, 2024, 44(1): 37-49.

图/表 5

表1

当 $M=5$ 时, 对于不同的 $N$ 前四个特征值 $\lambda_{MN}^i(i=1,2,3,4)$ 的数值结果"

表1

表2

当 $N=25$ , 对于不同的 $M$ 前四个特征值 $\lambda_{N}^i(i=1,2,3,4)$ 的数值结果"

表2

表3

当 $M=20$ 时, 对于不同的 $N$ 前四个特征值 $\lambda_{MN}^i(i=1,2,3,4)$ 的数值结果"

表3

表4

当 $N=35$ 时, 对于不同的 $M$ 前四个特征值 $\lambda_{MN}^i(i=1,2,3,4)$ 的数值结果"

表4

图1

参考文献 23

[1]	An J, Li H Y, Zhang Z M. Spectral-Galerkin approximation and optimal error estimate for biharmonic eigenvalue problems in circular/spherical/elliptical domains. Numerical Algorithms, 2020, 84(2): 427-455 doi: 10.1007/s11075-019-00760-4
[2]	An J, Luo Z D. A high accuracy spectral method based on min/max principle for biharmonic eigenvalue problems on a spherical domain. Journal of Mathematical Analysis and Applications, 2016, 439(1): 385-395 doi: 10.1016/j.jmaa.2016.02.048
[3]	An J, Shen J. A Spectral-Element method for transmission eigenvalue problems. Journal of Scientific Computing, 2013, 57(3): 670-688 doi: 10.1007/s10915-013-9720-1
[4]	An J. A Legendre-Galerkin spectral approximation and estimation of the index of refraction for transmission eigenvalues. Applied Numerical Mathematics, 2016, 108: 171-184
[5]	BABU Š KA I, Osborn J. Eigenvalue problems. Handbook of Numerical Analysis, 1991, 2: 641-787
[6]	Banerjee U, Osborn J E. Estimation of the effect of numerical integration in finite element eigenvalue approximation. Numerische Mathematik, 1989, 56(8): 735-762 doi: 10.1007/BF01405286
[7]	Boffi D. Finite element approximation of eigenvalue problems. Acta Numerica, 2010, 19: 1-120 doi: 10.1017/S0962492910000012
[8]	Chen L Z, An J, Zhuang Q Q. Direct solvers for the biharmonic eigenvalue problems using Legendre polynomials. Journal of Scientific Computing, 2017, 70(3): 1030-1041 doi: 10.1007/s10915-016-0277-7
[9]	Chen L Z, Shen J, Xu C J. A triangular spectral method for the Stokes equations. Numerical Mathematics: Theory, Methods and Applications, 2011, 4(2): 158-179
[10]	Dubiner M. Spectral methods on triangles and other domains. Journal of Scientific Computing, 1991, 6(4): 345-390 doi: 10.1007/BF01060030
[11]	Fu H F, Rui H X, Hou J, et al. A stabilized mixed finite element method for elliptic optimal control problems. Journal of Scientific Computing, 2016, 66(3): 968-986 doi: 10.1007/s10915-015-0050-3
[12]	Ge Y X, Tan T, An J. A high accuracy numerical method and error analysis for fourth order elliptic eigenvalue problems in circular domain. Advances in Applied Mathematics and Mechanics, 2020, 12(3): 815-834 doi: 10.4208/aamm
[13]	Grebenkov D S, Nguyen B T. Geometrical structure of Laplacian eigenfunctions. SIAM Review, 2013, 55(4): 601-667 doi: 10.1137/120880173
[14]	Griffin A, Snoke D W, Stringari S. Bose-Einstein Condensation. Cambridge University Press, 1996
[15]	Kuttler J R. A finite-difference approximation for the eigenvalues of the clamped plate. Numerische Mathematik, 1971, 17(3): 230-238 doi: 10.1007/BF01436379
[16]	Lamichhane B P. A stabilized mixed finite element method for the biharmonic equation based on biorthogonal systems. Journal of Computational and Applied Mathematics, 2011, 235(17): 5188-5197 doi: 10.1016/j.cam.2011.05.005
[17]	Mercier B, Osborn J, Rappaz J, et al. Eigenvalue approximation by mixed and hybrid methods. Mathematics of Computation, 1981, 36(154): 427-453 doi: 10.1090/mcom/1981-36-154
[18]	Neese F. Prediction of electron paramagnetic resonance $g$ values using coupled perturbed Hartree-Fock and Kohn-Sham theory. Chem Phys, 2001, 115(24): 11080-11096
[19]	Pasquetti R, Rapetti F. Spectral element methods on unstructured meshes: Comparisons and recent advances. Journal of Scientific Computing, 2006, 27(1): 377-387 doi: 10.1007/s10915-005-9048-6
[20]	Rannacher R. Nonconforming finite element methods for eigenvalue problems in linear plate theory. Numerische Mathematik, 1979, 33(1): 23-42 doi: 10.1007/BF01396493
[21]	Shen J, Wang L L, Li H Y. A triangular spectral element method using fully tensorial rational basis functions. SIAM Journal on Numerical Analysis, 2009, 47(3): 1619-1650 doi: 10.1137/070702023
[22]	Sherwin S J, Karniadakis G E. A triangular spectral element method: Applications to the incompressible Navier-Stokes equations. Computer Methods in Applied Mechanics and Engineering, 1995, 123(1-4): 189-229 doi: 10.1016/0045-7825(94)00745-9
[23]	Tkatchenko A, Scheffler M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Physical Review Letters, 2009, 102(7): 073005 doi: 10.1103/PhysRevLett.102.073005

Metrics

Viewed

Full text

204

HTML			PDF

Just accepted	Online first	Issue	Just accepted	Online first	Issue
0	0	0	0	0	204

	From	local

	Times	204
	Rate	100%

Abstract

107

Just accepted	Online first	Issue

0	0	107

From	Others	local

Times	103	4
Rate	96%	4%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed