数学物理学报 ›› 2022, Vol. 42 ›› Issue (6): 1886-1897.
非线性伪单调方程组的谱LS型投影算法
- 重庆三峡学院数学与统计学院 重庆 404100
-
收稿日期:2022-03-22出版日期:2022-12-26发布日期:2022-12-16 -
通讯作者:刘金魁 E-mail:zhangning19990405@126.com;liujinkui2006@126.com -
作者简介:张宁, E-mail:zhangning19990405@126.com -
基金资助:重庆市自然科学基金(cstc2021jcyj-msxmX0233);重庆三峡学院研究生科研创新项目(YJSKY22058)
Spectral LS-type Projection Algorithm for Solving Nonlinear Pseudo-Monotone Equations
- School of Mathematics and Statistics, Chongqing Three Gorges University, Chongqing 404100
-
Received:2022-03-22Online:2022-12-26Published:2022-12-16 -
Contact:Jinkui Liu E-mail:zhangning19990405@126.com;liujinkui2006@126.com -
Supported by:the Chongqing Research Program of Basic Research and Frontier Technology(cstc2021jcyj-msxmX0233);the Chongqing Three Gorges University Graduate Research Innovation Project(YJSKY22058)
摘要:
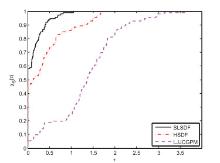
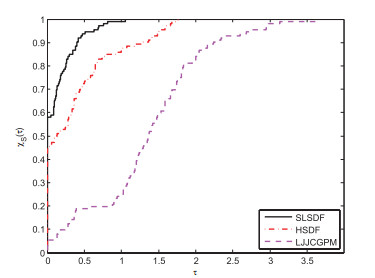
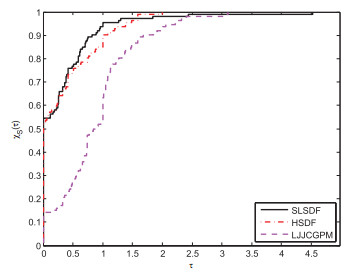
基于谱梯度法和著名LS共轭梯度法的结构, 该文建立了求解凸约束非线性伪单调方程组问题的谱LS型无导数投影算法.通过构建适当的谱参数, 该算法在每一次迭代中都能保证搜索方向的充分下降性, 并且独立于线搜索条件.在适当的假设条件和经典无导数线搜索条件下, 算法具有全局收敛性.通过数值实验发现, 该算法继承了LS共轭梯度法优秀的计算性能, 并提高了稳定性.
中图分类号:
- O241
引用本文
张宁,刘金魁. 非线性伪单调方程组的谱LS型投影算法[J]. 数学物理学报, 2022, 42(6): 1886-1897.
Ning Zhang,Jinkui Liu. Spectral LS-type Projection Algorithm for Solving Nonlinear Pseudo-Monotone Equations[J]. Acta mathematica scientia,Series A, 2022, 42(6): 1886-1897.
使用本文
表 1
算法对问题1的测试结果"
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
NI/time/    | NI/time/    | NI/time/    | ||
   | 10000 | 10/0.27/8.35775E-06 | 9/0.05/7.69126E-06 | 10/0.13/6.24219E-06 |
| 100000 | 11/0.54/5.36400E-06 | 10/0.35/4.40940E-06 | 13/0.44/3.06195E-06 | |
   | 10000 | 11/0.07/3.95144E-06 | 10/0.05/2.24586E-06 | 11/0.42/2.52040E-06 |
| 100000 | 12/0.59/2.53604E-06 | 10/0.35/7.10203E-06 | 11/0.36/1.95314E-06 | |
   | 10000 | 14/0.15/5.38909E-06 | 18/0.27/8.08404E-06 | 13/0.09/2.45327E-06 |
| 100000 | 15/0.63/3.45872E-06 | 19/0.84/8.64032E-06 | 13/0.48/7.75972E-06 | |
   | 10000 | 10/0.07/3.16713E-06 | 16/0.16/8.47098E-06 | 10/0.08/5.68024E-06 |
| 100000 | 11/0.62/1.47420E-06 | 17/0.74/9.05390E-06 | 11/0.35/7.97022E-06 | |
   | 10000 | 11/0.06/4.81393E-06 | 11/0.05/5.31729E-06 | 12/0.07/4.65517E-06 |
| 100000 | 12/0.52/3.08958E-06 | 12/0.45/3.04840E-06 | 11/0.32/4.10582E-06 | |
   | 1000 | 18/0.46/5.95037E-06 | 23/0.02/7.65046E-06 | 18/0.02/7.26018E-06 |
| 1000 | 14/0.01/2.53885E-06 | 17/0.02/2.36570E-06 | 17/0.01/3.03249E-06 | |
| 1000 | 18/0.01/2.69658E-06 | 16/0.01/9.89883E-06 | 19/0.01/4.60776E-06 | |
| 10000 | 16/0.25/3.56274E-06 | 19/0.1/8.93693E-06 | 20/0.07/2.70993E-06 | |
| 10000 | 17/0.09/8.58381E-06 | 16/0.06/8.76281E-06 | 24/0.08/3.85628E-06 | |
| 10000 | 16/0.08/2.41299E-06 | 21/0.08/3.38577E-06 | 20/0.06/4.22776E-06 |
表 2
算法对问题2的测试结果"
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
NI/time/    | NI/time/    | NI/time/    | ||
   | 10000 | 14/0.11/2.28152E-06 | 22/0.13/6.86367E-06 | 49/0.24/6.82665E-06 |
| 100000 | 16/1.03/2.10679E-06 | 25/1.44/6.43402E-06 | 54/2.08/6.77842E-06 | |
   | 10000 | 12/0.08/2.04626E-06 | 21/0.14/9.39860E-06 | 52/0.24/7.26662E-06 |
| 100000 | 19/1.16/1.76761E-06 | 24/1.23/5.72030E-06 | 51/1.87/7.03466E-06 | |
   | 10000 | 12/0.09/8.92636E-06 | 27/0.17/7.87962E-06 | 49/0.25/6.42977E-06 |
| 100000 | 15/0.92/4.24272E-06 | 24/1.43/7.22225E-06 | 53/2.02/6.98044E-06 | |
   | 10000 | 14/0.12/8.31650E-06 | 22/0.15/8.32467E-06 | 49/0.2/6.63369E-06 |
| 100000 | 23/1.57/3.13326E-06 | 29/1.64/9.69912E-06 | 59/2.12/8.06344E-06 | |
   | 10000 | 20/0.17/9.18226E-06 | 22/0.13/7.27369E-06 | 51/0.27/9.47091E-06 |
| 100000 | 18/1.75/5.89499E-06 | 23/1.16/5.15380E-06 | 54/1.98/7.31554E-06 | |
   | 1000 | 13/0.02/9.55053E-06 | 25/0.03/9.45970E-06 | 68/0.04/7.64093E-06 |
| 1000 | 13/0.01/6.91733E-06 | 26/0.02/6.77331E-06 | 58/0.03/7.69436E-06 | |
| 1000 | 14/0.01/3.27047E-06 | 22/0.01/9.13867E-06 | 58/0.02/7.50824E-06 | |
| 10000 | 16/0.1/4.89654E-06 | 42/0.28/5.62731E-06 | 64/0.28/9.72200E-06 | |
| 10000 | 19/0.13/5.67477E-06 | 40/0.22/8.89704E-06 | 64/0.26/9.52940E-06 | |
| 10000 | 18/0.12/4.61617E-06 | 27/0.16/7.33332E-06 | 63/0.31/9.64623E-06 |
表 3
算法对问题3的测试结果"
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
NI/time/    | NI/time/    | NI/time/    | ||
   | 10000 | 17/0.07/2.81228E-06 | 16/0.06/8.52110E-06 | 57/0.24/9.14599E-06 |
| 100000 | 16/0.39/8.13031E-06 | 20/0.49/6.11814E-06 | 44/0.81/8.87728E-06 | |
   | 10000 | 15/0.06/9.95448E-06 | 16/0.06/3.98212E-06 | 58/0.14/9.11972E-06 |
| 100000 | 15/0.39/4.47081E-06 | 18/0.42/4.45220E-06 | 45/0.81/8.73945E-06 | |
   | 10000 | 14/0.06/5.53121E-06 | 12/0.05/1.99091E-06 | 23/0.08/8.77438E-06 |
| 100000 | 15/0.36/5.62202E-06 | 15/0.37/9.14178E-06 | 40/0.73/7.49943E-06 | |
   | 10000 | 16/0.12/4.56086E-06 | 13/0.05/1.27684E-06 | 53/0.16/9.12098E-06 |
| 100000 | 18/0.41/9.53202E-06 | 18/0.42/2.94888E-06 | 40/0.73/9.09379E-06 | |
   | 10000 | 14/0.05/6.46989E-06 | 17/0.06/3.78712E-06 | 56/0.14/9.14812E-06 |
| 100000 | 17/0.41/8.76135E-06 | 15/0.34/7.77275E-06 | 41/0.72/8.76429E-06 | |
   | 1000 | 15/0.02/5.12728E-06 | 14/0.02/6.96159E-06 | 70/0.03/6.06227E-06 |
| 1000 | 16/0.01/3.31604E-06 | 15/0.01/5.33449E-06 | 71/0.02/6.04804E-06 | |
| 1000 | 15/0.01/8.42411E-06 | 17/0.01/3.22741E-06 | 67/0.02/9.92832E-06 | |
| 10000 | 17/0.06/3.04681E-06 | 17/0.07/1.89898E-06 | 57/0.15/9.11084E-06 | |
| 10000 | 17/0.06/3.77356E-06 | 17/0.05/3.52052E-06 | 57/0.12/9.21500E-06 | |
| 10000 | 17/0.05/3.04315E-06 | 16/0.04/6.01119E-06 | 53/0.12/9.08530E-06 |
表 4
算法对问题4的测试结果"
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
NI/time/    | NI/time/    | NI/time/    | ||
   | 10000 | 34/0.15/6.71745E-06 | 22/0.08/9.64604E-06 | 58/0.17/8.00695E-06 |
| 100000 | 40/1.33/5.98689E-06 | 30/0.88/4.99211E-06 | 56/1.22/6.92717E-06 | |
   | 10000 | 33/0.12/6.46636E-06 | 26/0.11/9.37117E-06 | 61/0.17/7.19919E-06 |
| 100000 | 33/1.04/8.47901E-06 | 31/0.96/4.23145E-06 | 58/1.3/9.11678E-06 | |
   | 10000 | 37/0.15/5.39551E-06 | 31/0.12/6.05411E-06 | 65/0.19/8.18695E-06 |
| 100000 | 40/1.32/7.67252E-06 | 33/1.01/6.90460E-06 | 62/1.39/7.08876E-06 | |
   | 10000 | 30/0.13/4.75619E-06 | 30/0.11/6.52395E-06 | 70/0.17/7.42661E-06 |
| 100000 | 40/1.31/6.29701E-06 | 37/1.17/4.36692E-06 | 68/1.48/7.09583E-06 | |
   | 10000 | 30/0.12/8.35595E-06 | 28/0.12/8.82222E-06 | 57/0.14/9.92298E-06 |
| 100000 | 37/1.12/7.90263E-06 | 26/0.73/7.80168E-06 | 55/1.21/8.54528E-06 | |
   | 1000 | 42/0.03/7.25125E-06 | 37/0.03/6.49794E-06 | 84/0.03/7.28839E-06 |
| 1000 | 50/0.02/8.09325E-06 | 31/0.01/8.94628E-06 | 70/0.02/9.50344E-06 | |
| 1000 | 50/0.02/8.03816E-06 | 38/0.01/7.83207E-06 | 79/0.02/8.27614E-06 | |
| 10000 | 45/0.19/4.45461E-06 | 47/0.16/4.26260E-06 | 104/0.23/9.05904E-06 | |
| 10000 | 55/0.19/5.31741E-06 | 40/0.12/7.73662E-06 | 92/0.19/8.53725E-06 | |
| 10000 | 56/0.18/5.93166E-06 | 42/0.14/7.89234E-06 | 90/0.2/9.27884E-06 |
表 5
算法对问题5的测试结果"
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
NI/time/    | NI/time/    | NI/time/    | ||
   | 10000 | 15/0.2/9.30794E-06 | 24/0.26/8.99460E-06 | 53/0.41/7.45327E-06 |
| 100000 | 25/2.93/6.43615E-06 | 19/1.78/8.38742E-06 | 55/4.19/9.53306E-06 | |
   | 10000 | 17/0.25/8.73580E-06 | 26/0.29/9.71544E-06 | 57/0.46/8.26386E-06 |
| 100000 | 34/3.94/6.56639E-06 | 21/2.03/8.86982E-06 | 60/4.54/6.42017E-06 | |
   | 10000 | 37/0.45/6.52915E-06 | 31/0.35/6.52281E-06 | 199/1.46/9.56048E-06 |
| 100000 | 54/6.35/7.12462E-06 | 26/2.58/9.96656E-06 | 200/13.6/8.85841E-06 | |
   | 10000 | 33/0.41/3.86804E-06 | 29/0.34/4.86781E-06 | 63/0.5/8.09248E-06 |
| 100000 | 49/5.59/6.35406E-06 | 29/2.91/9.44800E-06 | 62/4.71/7.91238E-06 | |
   | 10000 | 19/0.25/7.35353E-06 | 27/0.3/7.77302E-06 | 59/0.5/8.37336E-06 |
| 100000 | 32/3.82/6.28651E-06 | 23/2.34/5.85602E-06 | 55/4.19/6.79479E-06 | |
   | 1000 | 23/0.04/9.62598E-06 | 31/0.05/8.91162E-06 | 201/0.15/8.25980E-06 |
| 1000 | 25/0.03/5.50717E-06 | 34/0.04/9.17404E-06 | 197/0.14/7.45662E-06 | |
| 1000 | 24/0.03/3.32316E-06 | 34/0.04/7.69712E-06 | 64/0.05/9.94895E-06 | |
| 10000 | 33/0.4/3.16616E-06 | 34/0.47/8.97918E-06 | 67/0.49/7.79202E-06 | |
| 10000 | 37/0.43/8.07076E-06 | 33/0.33/8.94202E-06 | 67/0.49/7.33025E-06 | |
| 10000 | 28/0.38/5.46344E-06 | 38/0.42/5.74752E-06 | 69/0.49/7.27176E-06 |
表 6
算法对问题6的测试结果"
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
NI/time/    | NI/time/    | NI/time/    | ||
   | 10000 | 12/0.04/3.53915E-06 | 10/0.04/1.82363E-06 | 26/0.05/7.73313E-06 |
| 100000 | 13/0.28/2.65924E-06 | 10/0.19/5.76683E-06 | 28/0.4/6.73508E-06 | |
   | 10000 | 13/0.04/3.17492E-06 | 10/0.04/4.73744E-06 | 23/0.05/7.15729E-06 |
| 100000 | 14/0.32/2.38556E-06 | 11/0.21/1.76149E-06 | 25/0.42/6.23357E-06 | |
   | 10000 | 9/0.03/1.67451E-06 | 11/0.04/1.43408E-06 | 23/0.05/6.28294E-06 |
| 100000 | 9/0.18/5.29525E-06 | 11/0.19/4.53495E-06 | 25/0.39/5.47206E-06 | |
   | 10000 | 11/0.03/6.75249E-06 | 11/0.03/1.44773E-06 | 25/0.05/6.65329E-06 |
| 100000 | 12/0.24/5.07367E-06 | 11/0.21/4.57811E-06 | 27/0.41/5.79461E-06 | |
   | 10000 | 12/0.04/7.54576E-06 | 11/0.03/1.80320E-06 | 26/0.05/9.15601E-06 |
| 100000 | 13/0.27/5.66971E-06 | 11/0.19/5.70223E-06 | 28/0.42/7.97432E-06 | |
   | 1000 | 15/0.01/4.65847E-06 | 21/0.02/8.13107E-06 | 30/0.02/8.92921E-06 |
| 1000 | 62/0.01/5.37181E-06 | 124/0.04/9.46999E-06 | 376/0.05/9.07041E-06 | |
| 1000 | 36/0.01/6.96704E-06 | 114/0.03/8.90380E-06 | 283/0.04/9.54975E-06 | |
| 10000 | 67/0.13/8.04304E-06 | 38/0.07/8.47795E-06 | 254/0.33/7.17963E-06 | |
| 10000 | 29/0.06/7.79403E-06 | 28/0.05/9.51788E-06 | 142/0.18/7.03547E-06 | |
| 10000 | 30/0.05/7.67295E-06 | 32/0.06/8.66574E-06 | 371/0.43/7.84702E-06 |
表 7
算法对问题7的测试结果"
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
NI/time/    | NI/time/    | NI/time/    | ||
   | 10000 | 6/0.03/3.45393E-07 | 17/0.06/5.54564E-06 | 18/0.05/5.65483E-06 |
| 100000 | 6/0.2/1.09223E-06 | 18/0.44/6.05833E-06 | 19/0.38/6.55944E-06 | |
   | 10000 | 6/0.03/6.20504E-07 | 16/0.05/4.33525E-06 | 18/0.05/8.39471E-06 |
| 100000 | 6/0.2/1.96221E-06 | 17/0.52/4.73604E-06 | 19/0.4/9.73760E-06 | |
   | 10000 | 7/0.03/4.59950E-07 | 17/0.06/8.08326E-06 | 17/0.05/5.97154E-06 |
| 100000 | 7/0.24/1.45449E-06 | 18/0.44/8.83056E-06 | 18/0.35/6.92680E-06 | |
   | 10000 | 5/0.02/4.07959E-06 | 17/0.06/6.42071E-06 | 18/0.05/6.74412E-06 |
| 100000 | 6/0.18/2.53313E-07 | 18/0.43/7.01431E-06 | 19/0.39/7.82298E-06 | |
   | 10000 | 5/0.03/3.42253E-07 | 14/0.05/9.48173E-06 | 15/0.05/8.28338E-06 |
| 100000 | 5/0.16/1.08230E-06 | 16/0.42/3.57842E-06 | 16/0.33/9.60847E-06 | |
   | 1000 | 14/0.01/8.67102E-07 | 17/0.02/5.33128E-06 | 17/0.02/8.07045E-06 |
| 1000 | 13/0.01/9.50521E-06 | 17/0.01/5.32577E-06 | 17/0.01/8.23321E-06 | |
| 1000 | 15 0.01/7.80850E-06 | 17/0.01/5.27943E-06 | 17/0.01/7.88612E-06 | |
| 10000 | 14/0.05/6.96719E-06 | 18/0.05/5.81512E-06 | 18/0.05/9.32633E-06 | |
| 10000 | 14/0.04/5.16981E-06 | 18/0.06/5.81045E-06 | 18/0.04/9.52345E-06 | |
| 10000 | 14/0.04/6.15402E-06 | 18/0.04/5.82664E-06 | 18/0.03/9.36081E-06 |
| 1 | Dennis J E , Schnabel R B . Numerical Methods for Unconstrained Optimization and Nonlinear Equations. Philadelphia: SIAM, 1983 |
| 2 | Solodov M V , Svaiter B F . A Globally Convergent Inexact Newton Method for Systems of Monotone Equations. Kluwer: Kluwer Academic Publisher, 1988 |
| 3 |
Zhou G , Toh K C . Superline convergence of a Newton-type algorithm for monotone equations. Journal of Optimization Theory and Applications, 2005, 125, 205- 221
doi: 10.1007/s10957-004-1721-7 |
| 4 |
Li D H , Fukushima M . A globally and superlinearly convergent Gauss-Newton based BFGS method for symmetric equations. SIAM Journal on Numerical Analysis, 1999, 37, 152- 172
doi: 10.1137/S0036142998335704 |
| 5 |
Zhou W J . A modified BFGS type quasi-Newton method with line search for symmetric nonlinear equations problems. Journal of Computational and Applied Mathematics, 2020, 367, 112454
doi: 10.1016/j.cam.2019.112454 |
| 6 |
Cheng W Y . A PRP type method for systems of monotone equations. Mathematical and Computer Modelling, 2009, 50, 15- 20
doi: 10.1016/j.mcm.2009.04.007 |
| 7 |
Yu Z S , Ji L , Sun J , et al. Spectral gradient projection method for monotone nonlinear equations with convex constraints. Applied Numerical Mathematics, 2009, 59, 2416- 2423
doi: 10.1016/j.apnum.2009.04.004 |
| 8 |
Koorapetse M , Kaelo P . A derivative-free conjugate gradient projection method based on the memoryless BFGS update. Malaya Journal of Matematik, 2020, 8, 502- 509
doi: 10.26637/MJM0802/0031 |
| 9 |
Livieris I E , Tampakas V , Pintelas P . A descent hybrid conjugate gradient method based on the memoryless BFGS update. Numerical Algorithms, 2018, 79, 1169- 1185
doi: 10.1007/s11075-018-0479-1 |
| 10 | Liu P J , Jian J B , Jiang X Z . A new conjugate gradient projection method for convex constrained nonlinear equations. Complexity, 2020, 2020, 1- 14 |
| 11 |
刘金魁, 孙悦, 赵永祥. 凸约束伪单调方程组的无导数投影算法. 计算数学, 2021, 43, 388- 400
doi: 10.12286/jssx.j2020-0659 |
|
Liu J K , Sun Y , Zhao Y X . A derivative-free projection algorithm for solving pseudo-monotone equations with convex constraints. Mathematica Numerica Sinica, 2021, 43, 388- 400
doi: 10.12286/jssx.j2020-0659 |
|
| 12 |
Gao P T , He C J . An efficient three-term conjugate gradient method for nonlinear monotone equations with convex constraints. Calcolo, 2018, 55, 1- 17
doi: 10.1007/s10092-018-0244-9 |
| 13 | Liu J K , Lu Z L , Xu J L , et al. An efficient projection-based algorithm without Lipschitz continuity for large-scale nonlinear pseudo-monotone equations. Journal of Computational and Applied Mathematics, 2021, 403, 113822 |
| 14 | Bing Y , Lin G . An efficient implementation of Merrill's method for sparse or partially separable systems of nonlinear equations. SIAM Journal on Optimization, 1991, 2, 206- 221 |
| 15 |
Conn A R , Gould N I M , Toint Ph L . CUTEr: constrained and unconstrained testing enviroment. ACM Transactions on Mathematical Software, 1995, 21, 123- 160
doi: 10.1145/200979.201043 |
| 16 |
Moŕe J J , Garbow B S , Hillström K E . Testing uncosntrained optimization software. ACM Transactions on Mathematical Software, 1981, 7, 17- 41
doi: 10.1145/355934.355936 |
| 17 | Waziri M Y , Muhammad H U , Halilu A S , Ahmed K . Modified matrix-free methods for solving system of nonlinear equations. Optimization, 2021, 71, 2321- 2340 |
| 18 |
Dolan E D , Moŕe J J . Benchmarking optimization software with performance profiles. Mathematical Programming, 2002, 91, 201- 213
doi: 10.1007/s101070100263 |
| [1] | 潘庭葳,贺素香. 双重稀疏约束优化问题的一种贪婪单纯形算法[J]. 数学物理学报, 2022, 42(3): 920-933. |
| [2] | 袁功林,吴宇伦,PhamHongtruong. 基于非单调线搜索的HS-DY形共轭梯度方法及在图像恢复中的应用[J]. 数学物理学报, 2022, 42(2): 605-620. |
| [3] | 朱志斌,耿远航. 一个改进的WYL型三项共轭梯度法[J]. 数学物理学报, 2021, 41(6): 1871-1879. |
| [4] | 谢亚君. 一类基于Halley-Newton型的有效修正算法[J]. 数学物理学报, 2021, 41(4): 1066-1078. |
| [5] | 马国栋. 强Wolfe线搜索下的修正PRP和HS共轭梯度法[J]. 数学物理学报, 2021, 41(3): 837-847. |
| [6] | 迟晓妮,曾荣,刘三阳,朱志斌. 对称锥权互补问题的正则化非单调非精确光滑牛顿法[J]. 数学物理学报, 2021, 41(2): 507-522. |
| [7] | 马国栋. 一般约束极大极小优化问题一个强收敛的广义梯度投影算法[J]. 数学物理学报, 2020, 40(3): 641-649. |
| [8] | 赵金虎, 刘白羽, 徐尔. 一类完全非线性椭圆型方程组解的对称性[J]. 数学物理学报, 2015, 35(2): 312-323. |
| [9] | 胡朝明, 万中, 王旭. 一种新的非单调谱共轭梯度算法[J]. 数学物理学报, 2013, 33(1): 78-88. |
| [10] | 汤京永, 贺国平. 二阶锥规划的一步光滑牛顿法[J]. 数学物理学报, 2012, 32(4): 768-778. |
| [11] | 房亮, 贺国平, 王永丽. 带有P0函数的非线性互补问题的一个新的非内点连续算法[J]. 数学物理学报, 2011, 31(1): 229-238. |
| [12] | 张丽; 周伟军. Armijo线性搜索下Hager-Zhang共轭梯度法的全局收敛性[J]. 数学物理学报, 2008, 28(5): 840-845. |
| [13] | 童小娇;何伟. 解非线性约束方程的拉格朗日全局投影方法[J]. 数学物理学报, 2008, 28(1): 96-108. |
| [14] | 周长银; 贺国平; 王永丽. 基于有效约束识别技术的一个SSLE算法及其收敛性分析[J]. 数学物理学报, 2007, 27(3): 535-540. |
| [15] | 高自友, 任华玲, 贺国平. 无严格互补松驰条件的序列线性方程组新算法[J]. 数学物理学报, 2004, 24(3): 275-284. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 167
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 86
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|