数学物理学报 ›› 2022, Vol. 42 ›› Issue (6): 1812-1825.
有限理性下不确定性群体博弈弱NS平衡的稳定性
- 贵州大学数学与统计学院, 贵阳 550025
-
收稿日期:2021-08-12出版日期:2022-12-26发布日期:2022-12-16 -
通讯作者:杨光惠 E-mail:lucymingting@163.com;ghuiyang@126.com;hui-yang@163.com -
作者简介:王明婷, E-mail:lucymingting@163.com |杨辉, E-mail:hui-yang@163.com -
基金资助:国家自然科学基金项目(11271098);贵州省科技计划项目(黔科合基础[2019]1067号);贵州大学引进人才科研项目([2017]59);贵州省教学改革项目(201908)
Stability of Weak NS Equilibria for Population Games with Uncertain Parameters Under Bounded Rationality
Mingting Wang( ),Guanghui Yang*(
),Guanghui Yang*( ),Hui Yang(
),Hui Yang( )
)
- College of Mathematics and Statistics, Guizhou University, Guiyang 550025
-
Received:2021-08-12Online:2022-12-26Published:2022-12-16 -
Contact:Guanghui Yang E-mail:lucymingting@163.com;ghuiyang@126.com;hui-yang@163.com -
Supported by:the NSFC(11271098);the Guizhou Provincial Science and Technology Foundation(黔科合基础[2019]1067号);the Talent Introduction Research Foundation of Guizhou University([2017]59);the Educational Reform Foundation of Guizhou Province(201908)
摘要:
对不确定参数下群体博弈, 基于策略调整过程中产生相应成本这一事实, 该文提出了一种新的平衡——弱NS平衡, 其思想是当给定不确定参数时, 代理人因转变策略所获得的新增收益小于或等于其所增加的成本, 并且在不确定参数的作用下都不会得到严格差的纯收益, 因而代理人没有动力改变当前策略从而达到弱NS平衡.进一步, 运用Kakutani不动点定理证明了弱NS平衡的存在性; 其次, 通过构造抽象的理性函数, 建立相应的有限理性模型, 证明了当纯收益函数发生扰动时, 有限理性模型结构稳定进而对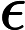
中图分类号:
- O225
引用本文
王明婷,杨光惠,杨辉. 有限理性下不确定性群体博弈弱NS平衡的稳定性[J]. 数学物理学报, 2022, 42(6): 1812-1825.
Mingting Wang,Guanghui Yang,Hui Yang. Stability of Weak NS Equilibria for Population Games with Uncertain Parameters Under Bounded Rationality[J]. Acta mathematica scientia,Series A, 2022, 42(6): 1812-1825.
使用本文
| 1 |
Nash J . Equilibrium points in n-person games. P Natl Acad Sci, 1950, 36 (1): 48- 49
doi: 10.1073/pnas.36.1.48 |
| 2 | Sandholm W H . Population Games and Evolutionary Dynamics. London: MIT Press, 2011 |
| 3 |
Lahkar R . Large population aggregative potential games. Dyn Games Appl, 2017, 7 (3): 443- 467
doi: 10.1007/s13235-016-0190-6 |
| 4 |
Cheung M W , Lahkar R . Nonatomic potential games: the continuous strategy case. Games Econ Behav, 2018, 108, 341- 362
doi: 10.1016/j.geb.2017.12.004 |
| 5 |
Chow S N , Li W , Lu J , et al. Population games and discrete optimal transport. J Nonlinear Sci, 2019, 29, 871- 896
doi: 10.1007/s00332-018-9507-5 |
| 6 | 杨光惠, 杨辉. 有限理性下群体博弈Nash平衡的稳定性. 贵州大学学报(自然科学版), 2019, 36 (5): 1- 3 1-3, 17 |
| Yang G H , Yang H . Stability of Nash equilibria of population games under bounded rationality. Journal of Guizhou University (Natural Sciences), 2019, 36 (5): 1- 3 1-3, 17 | |
| 7 |
Yang G H , Yang H , Song Q Q . Stability of weighted Nash equilibria for multiobjective population games. J Nonlinear Sci Appl, 2016, 9, 4167- 4176
doi: 10.22436/jnsa.009.06.59 |
| 8 |
Yang G H , Yang H . Stability of weakly Pareto-Nash equilibria and Pareto-Nash equilibria for multiobjective population games. Set-Valued Var Anal, 2017, 25, 427- 439
doi: 10.1007/s11228-016-0391-6 |
| 9 |
Yang Z , Zhang H . Essential stability of cooperative equilibria for population games. Optim Lett, 2019, 13 (7): 1573- 1582
doi: 10.1007/s11590-018-1303-5 |
| 10 |
Yang Z , Zhang H . NTU core, TU core and strong equilibria of coalitional population games with infinitely many pure strategies. Theory Decis, 2019, 87, 155- 170
doi: 10.1007/s11238-019-09701-y |
| 11 |
陈华鑫, 贾文生. 群体博弈的逼近定理及通有收敛性. 数学物理学报, 2021, 41A (5): 1566- 1573
doi: 10.3969/j.issn.1003-3998.2021.05.025 |
|
Chen H X , Jia W S . Approximation theorem and general convergence of population games. Acta Math Sci, 2021, 41A (5): 1566- 1573
doi: 10.3969/j.issn.1003-3998.2021.05.025 |
|
| 12 | Zhukovskii V I. Linear Quadratic Differential Games. Naoukova Doumka: Kiev, 1994 |
| 13 |
Larbani M , Lebbah H . A concept of equilibrium for a game under uncertainty. Eur J Oper Res, 1999, 117 (1): 145- 156
doi: 10.1016/S0377-2217(98)00079-4 |
| 14 |
张会娟, 张强. 不确定性下非合作博弈强Nash均衡的存在性. 控制与决策, 2010, 25 (8): 1251- 1254 1251-1254, 1260
doi: 10.13195/j.cd.2010.08.134.zhangkj.029 |
|
Zhang H J , Zhang Q . Existence of strong Nash equilibrium for non-cooperative games under uncertainty. Control and Decision, 2010, 25 (8): 1251- 1254 1251-1254, 1260
doi: 10.13195/j.cd.2010.08.134.zhangkj.029 |
|
| 15 | 张会娟, 张强. 不确定性下非合作博弈简单Berge均衡的存在性. 系统工程理论与实践, 2010, 30 (9): 1630- 1635 |
| Zhang H J , Zhang Q . Existence of simple Berge equilibrium for non-cooperative games under uncertainty. Systems Engineering Theory & Practice, 2010, 30 (9): 1630- 1635 | |
| 16 |
高静, 邬冬华, 张广. 不确定条件下n-人非合作博弈均衡点集的通有稳定性. 应用数学与计算数学学报, 2014, 28 (3): 336- 342
doi: 10.3969/j.issn.1006-6330.2014.03.010 |
|
Gao J , Wu D H , Zhang G . Generic stability of equilibrium for n-person non-cooperative games under uncertainty. Communications on Applied Mathematics and Computation, 2014, 28 (3): 336- 342
doi: 10.3969/j.issn.1006-6330.2014.03.010 |
|
| 17 | 邓喜才, 向淑文, 左羽. 不确定性下强Berge均衡的存在性. 运筹学学报, 2013, 17 (3): 101- 107 |
| Deng X C , Xiang S W , Zuo Y . Existence of strong Berge equilibrium under uncertainty. OR Transactions, 2013, 17 (3): 101- 107 | |
| 18 | 杨哲. 广义不确定性下非合作博弈中Berge-NS均衡的存在性. 系统科学与数学, 2015, 35 (9): 1073- 1080 |
| Yang Z . The existence theorems of Berge-NS equilibria in non-cooperative games under generized uncertainty. J Sys Sci & Math Scis, 2015, 35 (9): 1073- 1080 | |
| 19 |
陆辰超, 邬冬华. 不确定性下非合作博弈的有限理性模型及良定性. 应用数学与计算数学学报, 2016, 30 (3): 339- 348
doi: 10.3969/j.issn.1006-6330.2016.03.003 |
|
Lu C C , Wu D H . Bounded rationality and well-posedness in non-cooperative games under uncertainty. Communications on Applied Mathematics and Computation, 2016, 30 (3): 339- 348
doi: 10.3969/j.issn.1006-6330.2016.03.003 |
|
| 20 | 杨哲, 蒲勇健, 郭心毅. 不确定性下多目标博弈中弱Pareto-NS均衡的存在性. 系统工程理论与实践, 2013, 33 (3): 660- 665 |
| Yang Z , Pu Y J , Guo X Y . On the existence of weakly Pareto-NS equilibrium points in multi-objective games under uncertainty. Systems Engineering Theory&Practice, 2013, 33 (3): 660- 665 | |
| 21 | 赵薇, 杨辉, 吴隽永. 不确定参数下群体博弈均衡的存在性与通有稳定性. 应用数学学报, 2020, 43 (4): 627- 638 |
| Zhao W , Yang H , Wu J Y . Existence and generic stability of equilibria for population games with uncertain parameters. Acta Math Appl Sin, 2020, 43 (4): 627- 638 | |
| 22 | Zhao W, Yang H, Deng X C, et al. Stability of equilibria for population games with uncertain parameters under bounded rationality. J Inequal Appl, 2021, 2021(1): Article number 15 |
| 23 | Anderlini L , Canning D . Structural stability implies robustness to bounded rationality. J Econ Theory, 2001, 101 (2): 395- 422 |
| 24 | Yu C , Yu J . On structural stability and robustness to bounded rationality. Nonlinear Anal-TMA, 2006, 65 (3): 583- 592 |
| 25 | Yu J , Yang H , Yu C . Structural stability and robustness to bounded rationality for non-compactcases. J Glob Optim, 2009, 44, 149- 157 |
| 26 | Yu C , Yu J . Bounded rationality in multiobjective games. Nonlinear Anal-TMA, 2007, 67 (3): 930- 937 |
| 27 | 王红蕾, 俞建. 有限理性与多目标最优化问题弱有效解集的稳定性. 中国管理科学, 2008, 16 (4): 155- 158 |
| Wang H L , Yu J . Bounded rationality and stability of weakly efficient solution set of multiobjective optimization problems. Chinese Journal of Management Science, 2008, 16 (4): 155- 158 | |
| 28 | 王红蕾, 俞建. 有限理性与多目标问题解的稳定性. 运筹学学报, 2008, 12 (1): 104- 108 |
| Wang H L , Yu J . Bounded rationality and stability of solution of multiobjective optimization problems. OR Transactions, 2008, 12 (1): 104- 108 | |
| 29 | 俞建. 几类考虑有限理性平衡问题解的稳定性. 系统科学与数学, 2009, 29 (7): 999- 1008 |
| Yu J . Bounded rationality and stability of solution of some equilibrium problems. J Sys Sci & Math Scis, 2009, 29 (7): 999- 1008 | |
| 30 | 俞建. 博弈论与非线性分析. 北京: 科学出版社, 2008 |
| Yu J . Game Theory and Nonlinear Analysis. Beijing: Science Press, 2008 | |
| 31 | 俞建. 有限理性与博弈论中平衡点集的稳定性. 北京: 科学出版社, 2017 |
| Yu J . Bounded Rationality and Stability of Equilibrium Set in Game Theory. Beijing: Science Press, 2017 | |
| 32 | 俞建, 贾文生. 有限理性研究的博弈论模型. 中国科学: 数学, 2020, 50 (9): 1375- 1386 |
| Yu J , Jia W S . Game model in the study of bounded rationality. Scientia Sinica Mathematica, 2020, 50 (9): 1375- 1386 | |
| 33 | 王能发. 有限理性下不确定性博弈均衡的稳定性. 应用数学学报, 2017, 40 (4): 562- 572 |
| Wang N F . The stability of equilibrium point for uncertain game under bounded rationality. Acta Math Appl Sin, 2017, 40 (4): 562- 572 | |
| 34 | 蔡阳洋, 向淑文. n人非合作博弈弱Nash均衡点的存在性. 重庆工商大学学报(自然科学版), 2020, 37 (1): 54- 58 |
| Cai Y Y , Xiang S W . The existence of weak Nash equilibria in n-person non-cooperative game. J Chongqing Technol & Business Univ (Nat Sci Ed), 2020, 37 (1): 54- 58 | |
| 35 | Klein E, Thompson A C. Theory of Correspondences. New York: Wiley, 1984 |
| [1] | 陈华鑫,贾文生. 群体博弈的逼近定理及通有收敛性[J]. 数学物理学报, 2021, 41(5): 1566-1573. |
| [2] | 丘小玲,贾文生. 有限理性下变分不等式的逼近定理[J]. 数学物理学报, 2019, 39(4): 730-737. |
| [3] | 郑箫箫, 孙中洋, 张鑫. 模型不确定性及违约风险下的最优投资问题[J]. 数学物理学报, 2016, 36(2): 362-379. |
| [4] | 王志珍, 王龙, 郁文生. 两类时滞系统的鲁棒性分析[J]. 数学物理学报, 2004, 4(6): 717-722. |
| [5] | 杨昌利, 阮荣耀, 龚妙昆. 一类不确定性非线性系统的状态反馈鲁棒自适应控制器的设计与分析[J]. 数学物理学报, 2004, 24(1): 26-37. |
| [6] | 黄长水 阮荣耀. 一类具有有界扰动的非线性系统的输出反馈自适应控制[J]. 数学物理学报, 2000, 20(3): 405-413. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 143
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 132
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|