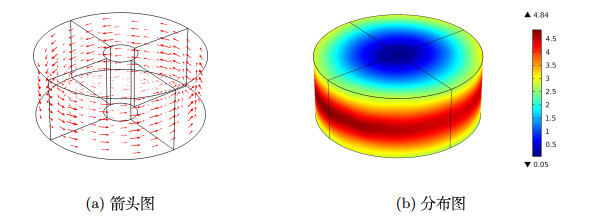
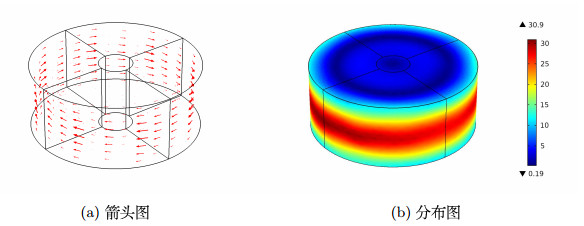
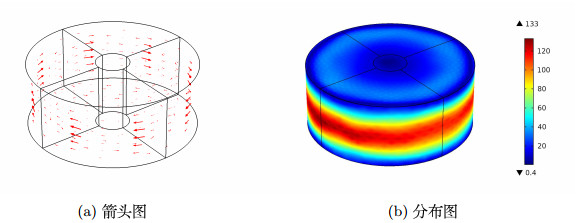
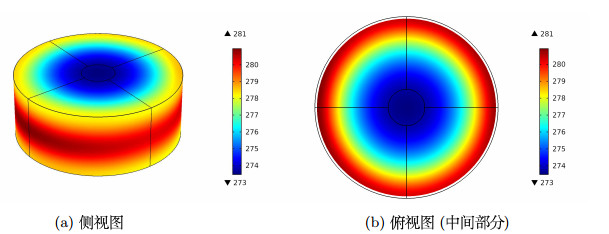
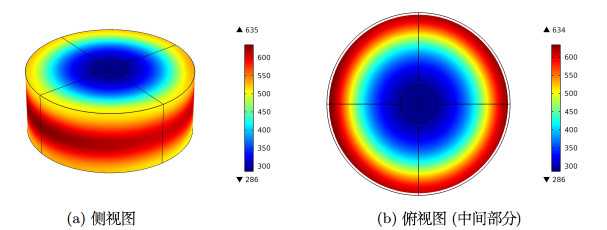
| 1 |
Akrivis G , Larsson S . Linearly implicit finite element methods for the time dependent Joule heating problem. BIT Numerical Mathematics, 2005, 45: 429- 442
doi: 10.1007/s10543-005-0008-1
|
| 2 |
Barglik J , Doležel I , Karban P , et al. Modelling of continual induction hardening in quasi-coupled formulation. Compel-the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2005, 24 (1): 251- 260
doi: 10.1108/03321640510571273
|
| 3 |
Bermúdez A , Gómez D , Muniz M C , et al. Transient numerical simulation of a thermoelectrical problem in cylindrical induction heating furnaces. Advances in Computational Mathematics, 2007, 26: 39- 62
doi: 10.1007/s10444-005-7470-9
|
| 4 |
Bień M . Global solutions of the non-linear problem describing Joule's heating in three space dimensions. Mathematical Methods in the Applied Sciences, 2005, 28 (9): 1007- 1030
doi: 10.1002/mma.559
|
| 5 |
Bossavit A , Emson C , Mayergoyz I D . Méthodes Numériques en Électromagnétisme. Paris: Eyrolles, 1991
|
| 6 |
Chovan J , Geuzaine C , Slodička M . \bmA-ϕ formulation of a mathematical model for the induction hardening process with a nonlinear law for the magnetic field. Computer Methods in Applied Mechanics and Engineering, 2017, 321: 294- 315
doi: 10.1016/j.cma.2017.03.045
|
| 7 |
Elliott C M , Larsson S . A finite element model for the time-dependent Joule heating problem. Mathematics of Computation, 1995, 62 (212): 1433- 1453
|
| 8 |
Evans L C. Graduate Studies in Mathematics: Partial Differential Equations. Second ed. New York: American Mathematical Society, 2010
|
| 9 |
Hömberg D . A mathematical model for induction hardening including mechanical effects. Nonlinear Analysis: Real World Applications, 2004, 5 (1): 55- 90
doi: 10.1016/S1468-1218(03)00017-8
|
| 10 |
Hömberg D , Petzold T , Rocca E . Analysis and simulations of multifrequency induction hardening. Nonlinear Analysis: Real World Applications, 2005, 22: 84- 97
|
| 11 |
Kang T , Wang R , Zhang H . Potential field formulation based on decomposition of the electric field for a nonlinear induction hardening model. Communications in Applied Mathematics and Computational Science, 2019, 14 (2): 175- 205
doi: 10.2140/camcos.2019.14.175
|
| 12 |
Kang T , Wang R , Zhang H . Fully discrete \bmT-ψ finite element method to solve a nonlinear induction hardening problem. Numerical Methods for Partial Differential Equations, 2021, 37: 546- 582
doi: 10.1002/num.22540
|
| 13 |
Nečas J . Introduction to the Theory of Nonlinear Elliptic Equations. Chichester: John Wiley & Sons Ltd, 1986
|
| 14 |
Nédélec J C . Mixed finite elements in R3. Numerische Mathematick, 1980, 35: 315- 341
doi: 10.1007/BF01396415
|
| 15 |
Roubíček T . Nonlinear Partial Differential Equations with Applications. Berlin: Birkhöuser, 2005
|
| 16 |
Slodička M , Chovan J . Solvability for induction hardening including nonlinear magnetic field and controlled Joule heating. Applicable Analysis, 2017, 96: 2780- 2799
doi: 10.1080/00036811.2016.1243661
|
| 17 |
Sun D , Manoranjan V S , Yin H M . Numerical solutions for a coupled parabolic equations arising induction heating processes. Conference Publications, 2007, 2007 (Special): 956- 964
|
| 18 |
Vajnverg M . Variational Method and Method of Monotone Operators in the Theory of Nonlinear Equations. New York: John Wiley, 1973
|
| 19 |
Yin H M . On a nonlinear Maxwell's system in quasi-stationary electromagnetic fields. Mathematical Models and Methods in Applied Sciences, 2004, 14 (10): 1521- 1539
doi: 10.1142/S0218202504003787
|
| 20 |
Yin H M . Regularity of weak solution to Maxwell's equations and applications to microwave heating. Journal of Differential Equations, 2004, 200 (1): 137- 161
doi: 10.1016/j.jde.2004.01.010
|
| 21 |
Yin H M , Wei W . Regularity of weak solution for a coupled system arising from a microwave heating model. European Journal of Applied Mathematics, 2014, 25: 117- 131
doi: 10.1017/S0956792513000326
|
 ),Hong Zhang4
),Hong Zhang4