数学物理学报 ›› 2022, Vol. 42 ›› Issue (1): 216-227.
一个带重启步的改进PRP型谱共轭梯度法
- 广西民族大学数学与物理学院, 应用数学与人工智能研究中心 & 广西混杂计算与集成电路设计分析重点实验室 南宁 530006
-
收稿日期:2021-01-18出版日期:2022-02-26发布日期:2022-02-23 -
通讯作者:简金宝 E-mail:yl2811280@163.com;1436134351@qq.com;jianjb@gxu.edu.cn;1710703068@qq.com -
作者简介:江羡珍, E-mail:yl2811280@163.com |廖伟, E-mail:1436134351@qq.com |毋晓迪, E-mail:1710703068@qq.com -
基金资助:广西自然科学基金(2020GXNSFDA238017);广西自然科学基金(2018GXNSFAA281099);广西民族大学科研基金(2018KJQD02);广西民族大学研究生创新项目(gxun-chxp201909)
An Improved PRP Type Spectral Conjugate Gradient Method with Restart Steps
Xianzhen Jiang( ),Wei Liao(
),Wei Liao( ),Jinbao Jian*(
),Jinbao Jian*( ),Xiaodi Wu(
),Xiaodi Wu( )
)
- Center for Applied Mathematics and Artificial Intelligence & Guangxi Key Laboratory of Hybrid Compution and IC Design Analysis, College of Mathematics and Physics, Guangxi University for Nationalities, Nanning 530006
-
Received:2021-01-18Online:2022-02-26Published:2022-02-23 -
Contact:Jinbao Jian E-mail:yl2811280@163.com;1436134351@qq.com;jianjb@gxu.edu.cn;1710703068@qq.com -
Supported by:the NSF of Guangxi Province(2020GXNSFDA238017);the NSF of Guangxi Province(2018GXNSFAA281099);the Research Project of Guangxi University for Nationalities(2018KJQD02);the Innovation Project of Guangxi University for Nationalities Graduate Education(gxun-chxp201909)
摘要:
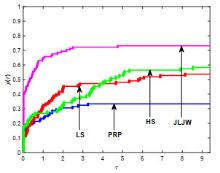
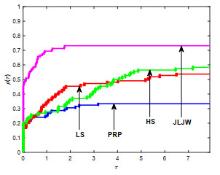
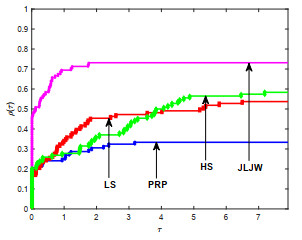
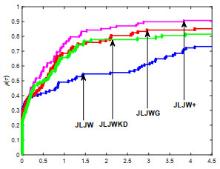
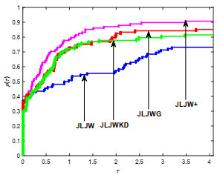
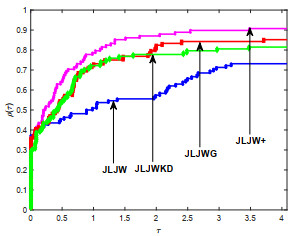
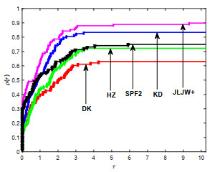
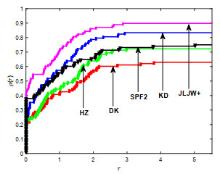
Polak-Ribière-Polak(PRP)方法是经典共轭梯度法中数值表现较好的方法之一.结合Wolfe非精确线搜索准则对PRP公式进行改进,从而产生新的共轭参数,并基于新共轭参数设计新的谱参数,引入重启条件并构造新的重启方向,进而建立一个带重启步的谱共轭梯度算法.在常规假设及强Wolfe非精确线搜索步长准则下,算法具有充分下降性和全局收敛性.最后,对算法进行中大规模数值实验并与当前公认数值效果较好的同类方法进行比较,结果表明新算法是很有效的.
中图分类号:
- O221
引用本文
江羡珍,廖伟,简金宝,毋晓迪. 一个带重启步的改进PRP型谱共轭梯度法[J]. 数学物理学报, 2022, 42(1): 216-227.
Xianzhen Jiang,Wei Liao,Jinbao Jian,Xiaodi Wu. An Improved PRP Type Spectral Conjugate Gradient Method with Restart Steps[J]. Acta mathematica scientia,Series A, 2022, 42(1): 216-227.
使用本文
表 1
数值试验报告"
| Problems | JLJW+ | KD | DK | HZ | SPF2 |
| Name/n | Itr/Tcpu/||g*|| | Itr/Tcpu/||g*|| | Itr/Tcpu/||g*|| | Itr/Tcpu/||g*|| | Itr/Tcpu/||g*|| |
| bard 3 | 1430/4.93/7.6e-07 | 1565/5.19/8.0e-07 | F/F/3.2e-05 | 620/2.00/4.0e-07 | 235/0.64/6.6e-07 |
| beale 2 | 631/0.96/3.6e-07 | 326/0.52/7.7e-07 | 86/0.11/1.6e-07 | 251/0.37/6.2e-07 | 142/0.20/4.3e-07 |
| box 3 | 150/0.26/2.1e-07 | 330/0.57/6.0e-07 | 134/0.26/1.4e-08 | 475/0.89/8.9e-07 | 91/0.13/5.2e-07 |
| cosine 300 | 19/0.03/5.2e-07 | 26/0.09/3.3e-07 | F/F/1.2e-04 | 32/0.06/4.9e-08 | F/F/3.0e+02 |
| cosine 1500 | 1560/11.26/1.5e-07 | F/F/1.4e+03 | F/F/2.8e+03 | F/F/1.2e+02 | F/F/1.8e+03 |
| cosine 4500 | F/F/2.9e+02 | F/F/5.8e-04 | F/F/1.2e+04 | 477/11.19/2.9e-07 | F/F/2.1e+03 |
| dixmaana 3000 | 18/0.99/3.4e-07 | 17/0.90/3.1e-07 | 23/1.22/6.0e-07 | 26/1.75/1.3e-07 | 24/1.38/1.9e-07 |
| dixmaana 12000 | 18/3.14/6.8e-07 | 17/2.93/6.2e-07 | 25/4.16/1.1e-07 | 21/3.70/1.6e-07 | 24/4.05/3.7e-07 |
| dixmaanb 3000 | 11/0.39/7.4e-07 | 12/0.50/3.3e-07 | 34/1.76/1.7e-07 | 49/3.92/9.6e-08 | 14/0.61/1.5e-07 |
| dixmaanb 12000 | 11/1.17/4.4e-07 | 12/1.51/5.8e-07 | 47/10.10/9.0e-08 | 40/10.30/6.5e-07 | 13/1.55/2.7e-07 |
| dixmaanc 3000 | 24/1.48/3.8e-08 | 25/1.54/5.5e-07 | 29/1.62/2.4e-07 | 33/2.20/1.9e-07 | 35/2.18/8.0e-07 |
| dixmaanc 12000 | 16/2.37/1.0e-06 | 25/4.38/4.5e-07 | 27/4.39/8.2e-07 | 73/18.86/5.6e-07 | 67/15.50/9.6e-07 |
| dixmaand 3000 | 25/1.28/1.3e-07 | 25/1.32/3.6e-07 | 29/1.56/3.3e-07 | 54/4.45/2.3e-07 | 45/2.73/6.7e-07 |
| dixmaand 12000 | 22/3.41/5.5e-07 | 23/3.67/6.5e-07 | 44/8.42/7.7e-07 | 29/5.73/7.2e-07 | 50/10.73/2.7e-07 |
| dixmaane 6000 | 1308/199.45/9.0e-07 | 1229/192.04/9.3e-07 | 1941/331.01/8.5e-07 | 1716/274.31/9.3e-07 | 564/82.65/7.7e-07 |
| dixmaanf 4500 | 775/94.63/8.3e-07 | 1258/161.65/7.9e-07 | 396/53.77/8.5e-07 | 1165/155.96/9.0e-07 | 470/59.77/7.1e-07 |
| dixmaanf 9000 | 1080/237.42/9.3e-07 | 1078/246.31/8.8e-07 | 1396/340.53/9.4e-07 | F/F/1.8e-05 | 383/80.92/4.1e-07 |
| dixmaang 7500 | 889/168.72/8.8e-07 | 1154/220.67/5.8e-07 | 1239/250.95/8.9e-07 | 1682/327.37/9.0e-07 | 614/112.05/9.5e-07 |
| dixmaanh 4500 | 1417/179.40/9.2e-07 | 1324/169.60/9.8e-07 | 1006/137.94/7.2e-07 | 953/120.53/9.9e-07 | 704/81.78/9.8e-07 |
| dixmaani 120 | 1930/9.09/8.7e-07 | 1595/7.68/6.7e-07 | F/F/1.2e-03 | F/F/8.4e-07 | 731/3.29/4.2e-07 |
| dixmaanj 2700 | 1193/94.28/8.5e-07 | 1382/108.65/6.2e-07 | 1320/110.36/9.5e-07 | F/F/1.0e-05 | 1153/85.27/6.4e-07 |
| dixmaank 3000 | 1142/98.31/6.5e-07 | 1158/100.76/7.8e-07 | F/F/4.0e-05 | F/F/2.7e-05 | 1799/154.65/6.6e-07 |
| dixmaanl 300 | 1554/14.02/9.8e-07 | 1424/12.64/8.9e-07 | F/F/4.6e-04 | F/F/8.0e-05 | 826/7.12/7.4e-07 |
| dixon3dq 50 | 1199/1.50/8.8e-07 | 1613/2.28/6.0e-07 | F/F/5.9e-05 | 1836/2.41/5.3e-07 | 629/0.82/6.0e-07 |
| dixon3dq 88 | 1934/2.80/8.3e-07 | 1476/2.09/6.7e-07 | F/F/1.0e-02 | F/F/4.9e-04 | 1227/1.65/5.2e-07 |
| dqdrtic 60000 | 496/35.92/7.8e-07 | 426/31.92/2.8e-07 | 197/13.41/4.1e-07 | 917/67.92/7.1e-07 | 312/21.78/6.2e-07 |
| dqrtic 100 | 22/0.06/5.7e-07 | 23/0.04/6.4e-07 | 34/0.04/7.7e-07 | 28/0.03/1.8e-07 | 60/0.12/1.8e-07 |
| dqrtic 450 | 34/0.13/2.8e-07 | 47/0.19/3.4e-07 | 33/0.15/7.4e-07 | 31/0.13/5.0e-07 | 60/0.36/5.7e-07 |
| edensch 10000 | 46/4.59/9.5e-07 | 54/6.25/6.2e-07 | F/F/8.7e-06 | F/F/3.8e-06 | F/F/3.3e-06 |
| edensch 50000 | 55/24.21/1.9e-07 | 65/29.17/8.8e-07 | F/F/1.0e-04 | F/F/1.8e-05 | F/F/1.2e-04 |
| edensch 100000 | 126/93.46/9.7e-07 | F/F/4.8e-05 | F/F/2.3e-05 | 120/139.38/5.3e-07 | F/F/2.0e-04 |
| eg2 30 | F/F/2.9e-06 | F/F/3.0e-01 | 313/0.43/8.0e-07 | F/F/3.2e-03 | F/F/1.1e-05 |
| eg2 80 | F/F/2.5e-04 | F/F/5.8e-06 | F/F/4.0e-01 | F/F/2.8e-02 | F/F/1.9e-05 |
| engval1 6 | 87/0.11/1.9e-07 | 95/0.14/2.4e-08 | F/F/4.7e-01 | F/F/8.8e-01 | F/F/1.8e-01 |
| fletchcr 10000 | 145/3.81/1.3e-07 | F/F/1.1e-03 | F/F/3.1e-04 | F/F/9.5e-04 | F/F/6.9e-04 |
| fletchcr 300000 | 211/118.78/3.9e-07 | F/F/9.2e-03 | F/F/6.2e-03 | F/F/9.5e-04 | F/F/2.6e-02 |
| freuroth 20 | 1700/2.52/9.8e-07 | 476/0.66/9.2e-07 | F/F/1.5e-05 | 455/0.60/6.8e-07 | F/F/6.8e-05 |
| freuroth 36 | F/F/2.2e-06 | F/F/6.3e-06 | F/F/8.2e-06 | F/F/6.5e-05 | F/F/7.5e-05 |
| genrose 2000 | 574/2.28/2.8e-07 | 399/1.94/4.1e-07 | 395/1.77/6.1e-07 | 1259/5.68/9.6e-07 | 692/2.85/4.4e-07 |
| genrose 47000 | 270/25.44/6.7e-07 | 336/31.54/1.3e-07 | 474/42.83/7.1e-07 | 854/76.03/9.0e-07 | 571/48.69/8.7e-07 |
| gulf 3 | 2/0.00/0.0e+00 | 2/0.00/0.0e+00 | 2/0.00/0.0e+00 | 2/0.00/0.0e+00 | 2/0.00/0.0e+00 |
| helix 3 | 479/1.02/1.6e-07 | 282/0.62/4.2e-07 | 316/0.60/7.0e-07 | 731/1.56/6.7e-07 | F/F/3.5e+03 |
| himmelbg 1000 | 3/0.01/1.6e-28 | 3/0.00/1.3e-28 | 3/0.00/1.6e-28 | 3/0.00/1.2e-28 | 3/0.00/1.6e-28 |
| himmelbg 10000 | 3/0.01/5.2e-28 | 3/0.01/4.2e-28 | 3/0.01/5.0e-28 | 3/0.01/3.8e-28 | 3/0.01/5.0e-28 |
| himmelbg 100000 | 3/0.10/1.6e-27 | 3/0.11/1.3e-27 | 3/0.12/1.6e-27 | 3/0.11/1.2e-27 | 3/0.12/1.6e-27 |
| kowosb 4 | 774/1.40/7.0e-07 | 817/1.55/4.7e-07 | 1574/3.07/8.7e-07 | F/F/5.2e-04 | 239/0.43/7.5e-07 |
| liarwhd 500 | 487/1.06/1.9e-07 | 750/1.63/9.4e-07 | 1168/2.52/8.5e-07 | F/F/2.9e-03 | 268/0.49/1.2e-07 |
| liarwhd 1000 | 534/1.43/2.3e-07 | F/F/1.3e-04 | F/F/1.6e-02 | 1267/3.35/9.8e-07 | 294/0.75/4.7e-07 |
| liarwhd 10000 | F/F/5.6e-02 | F/F/5.8e+00 | F/F/3.2e+03 | F/F/1.5e+03 | 409/8.96/8.9e-07 |
| nondquar 4 | F/F/1.2e-04 | F/F/5.0e-05 | F/F/4.9e-03 | 395/0.66/2.2e-07 | 87/0.12/6.5e-07 |
| penalty1 1000 | 15/0.82/1.2e-07 | 15/0.82/1.2e-07 | 15/0.86/1.2e-07 | 15/0.87/1.2e-07 | 15/0.89/1.2e-07 |
| penalty1 10000 | 9/28.41/9.6e-07 | 9/28.32/9.6e-07 | 9/28.02/9.6e-07 | 9/28.38/9.6e-07 | 9/28.46/9.6e-07 |
| quartc 100 | 22/0.04/5.7e-07 | 23/0.04/6.4e-07 | 34/0.05/7.7e-07 | 28/0.05/1.8e-07 | 60/0.13/1.8e-07 |
| quartc 450 | 34/0.14/2.8e-07 | 47/0.20/3.4e-07 | 33/0.14/7.4e-07 | 31/0.12/5.0e-07 | 60/0.31/5.7e-07 |
表 2
数值试验报告(续)"
| Problems | JLJW+ | KD | DK | HZ | SPF2 |
| Name/n | Itr/Tcpu/||g*|| | Itr/Tcpu/||g*|| | Itr/Tcpu/||g*|| | Itr/Tcpu/||g*|| | Itr/Tcpu/||g*|| |
| tridia 200 | 1491/2.44/3.2e-07 | 1380/2.41/9.8e-07 | 1699/2.90/9.3e-07 | F/F/5.9e-06 | 593/0.94/5.5e-07 |
| tridia 400 | 1905/3.90/5.7e-07 | F/F/1.1e-03 | F/F/8.8e-03 | F/F/3.8e-05 | 733/1.29/6.9e-07 |
| sinquad 3 | 406/0.57/4.7e-07 | 272/0.34/8.9e-07 | F/F/3.1e-04 | 501/0.63/3.0e-07 | 366/0.45/9.2e-07 |
| vardim 8 | 12/0.01/4.0e-08 | 12/0.01/4.0e-08 | 12/0.01/4.0e-08 | 12/0.01/4.0e-08 | 12/0.02/4.0e-08 |
| watson 3 | 107/0.26/2.6e-07 | 147/0.36/6.3e-07 | 51/0.12/2.1e-07 | 121/0.32/5.8e-07 | 108/0.31/9.8e-07 |
| woods 10000 | F/F/1.3e-02 | 792/20.82/9.5e-07 | 883/22.24/6.2e-07 | 922/22.70/8.8e-07 | 309/7.19/9.9e-07 |
| bdexp 1000 | 3/0.01/5.9e-107 | 3/0.00/7.1e-108 | 3/0.00/4.4e-107 | 3/0.00/2.5e-108 | 3/0.00/4.5e-107 |
| bdexp 10000 | 3/0.01/1.2e-109 | 3/0.01/9.4e-110 | 3/0.01/1.1e-109 | 3/0.01/8.4e-110 | 3/0.01/1.1e-109 |
| bdexp 100000 | 3/0.12/1.7e-109 | 3/0.13/1.7e-109 | 3/0.15/1.7e-109 | 3/0.15/1.7e-109 | 3/0.12/1.7e-109 |
| exdenschnf 1000 | 25/0.05/4.6e-07 | 68/0.18/2.4e-07 | 65/0.17/5.2e-07 | 91/0.35/3.8e-07 | 96/0.28/9.7e-07 |
| exdenschnf 10000 | 26/0.56/3.1e-07 | 68/2.43/7.6e-07 | 73/2.21/2.5e-07 | 85/2.85/2.6e-07 | 843/33.85/8.8e-07 |
| exdenschnf 100000 | 27/4.41/1.1e-07 | 69/15.80/6.0e-07 | 73/14.86/7.8e-07 | 59/12.45/2.2e-07 | 114/25.09/2.1e-07 |
| mccormak 2 | 21/0.05/9.3e-08 | 19/0.01/8.1e-07 | 63/0.07/9.0e-08 | 39/0.06/1.2e-07 | F/F/2.9e+04 |
| exdenschnb 1000 | 22/0.03/8.2e-08 | 27/0.05/8.0e-07 | 74/0.19/4.5e-07 | 32/0.05/3.5e-07 | 102/0.27/4.8e-07 |
| exdenschnb 10000 | 22/0.23/2.6e-07 | 28/0.40/7.1e-07 | 82/1.38/3.2e-07 | 25/0.29/1.0e-06 | 153/2.80/8.0e-07 |
| exdenschnb 100000 | 22/1.58/8.2e-07 | 30/2.59/2.6e-07 | 88/9.13/2.7e-07 | 29/2.19/4.5e-07 | 91/9.42/1.5e-07 |
| genquartic 5000 | 24/0.20/4.7e-07 | 31/0.32/9.0e-08 | 108/1.30/2.6e-07 | 33/0.22/8.6e-07 | 115/1.37/2.6e-07 |
| genquartic 30000 | 35/1.33/1.9e-07 | 38/1.37/2.0e-07 | 96/4.61/5.6e-07 | 36/1.43/7.0e-08 | 157/8.53/2.4e-07 |
| genquartic 100000 | 27/2.41/7.1e-08 | 37/3.79/5.2e-07 | 98/13.02/3.0e-07 | 81/11.20/8.8e-07 | 182/26.69/4.3e-07 |
| biggsb1 100 | 1240/1.82/6.9e-07 | 1381/1.97/9.8e-07 | F/F/2.9e-05 | F/F/7.2e-06 | 621/0.82/9.4e-07 |
| sine 4000 | 64/1.65/7.7e-09 | 180/4.19/1.3e-08 | F/F/8.0e-02 | 91/2.17/3.0e-07 | F/F/1.1e+03 |
| sine 20000 | 94/7.82/1.7e-09 | 181/14.39/6.0e-13 | F/F/9.7e-03 | 81/7.52/9.5e-07 | F/F/7.6e-04 |
| sine 40000 | 87/13.53/2.3e-08 | 394/67.01/7.9e-07 | F/F/5.0e-01 | 80/13.64/3.2e-07 | F/F/2.1e+03 |
| fletcbv3 8 | 43/0.04/5.3e-07 | 51/0.05/4.7e-07 | 47/0.05/7.7e-07 | 30/0.03/7.4e-07 | 52/0.05/3.9e-07 |
| nonscomp 2000 | 176/0.65/1.3e-07 | F/F/3.0e-03 | 100/0.37/4.2e-07 | F/F/4.6e-03 | F/F/5.0e-05 |
| nonscomp 10000 | 275/6.17/6.5e-07 | F/F/6.2e-02 | F/F/3.8e-02 | 413/9.78/4.7e-07 | F/F/1.2e-04 |
| power1 55 | 1699/2.30/9.5e-07 | F/F/5.1e-06 | F/F/1.4e-04 | F/F/3.6e-04 | 737/0.84/9.5e-07 |
| raydan1 2000 | 857/2.94/6.9e-07 | 1118/3.86/6.5e-07 | F/F/1.4e-04 | 1335/4.78/7.8e-07 | F/F/9.2e-05 |
| raydan1 3000 | 1252/8.69/7.5e-07 | F/F/2.5e-04 | F/F/2.6e-04 | F/F/3.8e-04 | F/F/2.3e-04 |
| raydan2 500 | 15/0.02/2.2e-07 | 18/0.02/1.2e-08 | 24/0.04/2.6e-08 | 21/0.03/8.5e-08 | 14/0.02/6.6e-08 |
| raydan2 5000 | 18/0.21/1.6e-07 | 21/0.28/7.2e-08 | 46/0.71/6.6e-07 | 38/0.56/2.7e-07 | 12/0.10/3.6e-07 |
| raydan2 50000 | 18/1.44/8.9e-07 | 19/1.65/5.7e-07 | 21/1.89/9.8e-07 | 22/1.90/9.3e-07 | 48/5.15/5.0e-07 |
| diagonal1 60 | 164/0.23/7.3e-07 | 88/0.09/9.4e-07 | 84/0.08/8.2e-07 | F/F/2.4e-06 | 179/0.28/8.7e-07 |
| diagonal1 100 | 242/0.34/1.7e-07 | F/F/2.6e-05 | F/F/3.3e-06 | 348/0.57/9.7e-07 | F/F/5.5e-06 |
| diagonal2 2000 | 1118/6.78/7.2e-07 | 1049/6.59/9.3e-07 | 334/1.97/6.9e-07 | 1988/12.48/7.6e-07 | 444/2.32/3.9e-07 |
| diagonal3 150 | F/F/2.3e-05 | 194/0.40/7.9e-07 | F/F/8.4e-06 | F/F/6.0e-06 | F/F/4.3e-05 |
| bv 2000 | 13/5.24/3.3e-07 | 14/5.79/3.1e-07 | 22/9.65/2.3e-07 | 9/3.23/4.6e-07 | 123/53.66/5.8e-07 |
| bv 20000 | 1/0.14/1.2e-08 | 1/0.00/1.2e-08 | 1/0.00/1.2e-08 | 1/0.00/1.2e-08 | 1/0.00/1.2e-08 |
| ie 100 | 15/1.33/2.8e-07 | 13/1.12/6.2e-07 | 20/1.94/5.0e-07 | 14/1.34/7.5e-07 | 38/4.96/6.6e-07 |
| ie 200 | 15/4.47/3.9e-07 | 13/3.56/7.2e-07 | 18/5.35/3.1e-07 | 17/5.68/9.3e-08 | 40/17.36/3.2e-07 |
| singx 200 | 348/2.28/7.4e-07 | 1218/7.82/6.3e-07 | F/F/3.5e-03 | F/F/7.0e-06 | 339/1.98/9.9e-07 |
| singx 1500 | 1105/318.57/6.4e-07 | 1940/559.01/9.8e-07 | F/F/6.3e-03 | F/F/1.8e-05 | 292/75.74/9.0e-07 |
| band 3 | 111/0.23/1.3e-07 | 67/0.12/6.3e-07 | 38/0.06/4.2e-07 | 77/0.11/6.9e-07 | 46/0.05/8.9e-08 |
| gauss 3 | 59/0.16/5.6e-07 | 47/0.10/6.4e-07 | 15/0.02/1.7e-07 | 14/0.03/8.1e-07 | 30/0.08/7.4e-07 |
| jensam 2 | 201/0.35/7.7e-07 | 119/0.19/6.7e-07 | 153/0.24/5.3e-07 | 211/0.39/7.0e-07 | 173/0.29/9.7e-07 |
| lin 100 | 2/0.01/2.0e-14 | 2/0.00/2.0e-14 | 2/0.00/2.0e-14 | 2/0.00/2.0e-14 | 2/0.00/2.0e-14 |
| lin 1000 | 12/83.01/1.3e-07 | 12/83.63/1.3e-07 | 12/82.60/1.3e-07 | 12/81.73/1.3e-07 | 12/82.49/1.3e-07 |
| osb2 11 | 1717/6.76/8.4e-07 | F/F/2.5e-03 | F/F/8.2e-04 | F/F/6.4e-04 | F/F/4.9e-03 |
| pen1 55 | 626/1.47/6.2e-07 | 448/1.02/9.2e-07 | 1475/3.47/9.5e-07 | 839/1.99/4.7e-07 | 106/0.18/1.5e-08 |
| pen2 100 | F/F/4.1e-05 | 274/2.25/6.2e-07 | F/F/1.1e-05 | 430/3.57/9.0e-07 | F/F/1.6e-05 |
| rosex 40 | F/F/7.3e-04 | 1077/2.00/5.3e-07 | 1496/2.58/9.4e-07 | 828/1.45/5.5e-07 | 141/0.18/7.1e-07 |
| sing 4 | 545/0.97/4.7e-07 | 380/0.60/6.7e-07 | F/F/5.0e-04 | F/F/5.5e-06 | 254/0.50/3.4e-08 |
| trid 500 | F/F/7.2e-05 | 899/55.29/1.0e-06 | F/F/1.5e-02 | 410/24.09/8.6e-07 | F/F/1.4e-04 |
| trid 1000 | 500/76.37/7.1e-07 | 211/29.37/3.9e-07 | F/F/4.5e-04 | 754/111.54/8.3e-07 | 391/55.48/9.2e-07 |
| 1 |
Hestenes M R , Stiefel E . Method of conjugate gradient for solving linear equations. Journal of Research of National Bureau of Standards, 1952, 49: 409- 436
doi: 10.6028/jres.049.044 |
| 2 |
Fletcher R , Reeves C . Function minimization by conjugate gradients. Computer Journal, 1964, 7 (2): 149- 154
doi: 10.1093/comjnl/7.2.149 |
| 3 | Polak E , Ribiére G . Note surla convergence de directions conjugées. Revue Francaise Informat Recherche Operationelle 3e Anneé, 1969, 16 (3): 35- 43 |
| 4 |
Polyak B T . The conjugate gradient method in extreme problems. USSR Computational Mathematics and Mathematical Physics, 1969, 9: 94- 112
doi: 10.1016/0041-5553(69)90035-4 |
| 5 |
Dai Y H , Yuan Y X . A nonlinear conjugate gradient method with a strong global convergence property. SIAM Journal on Optimization, 1999, 10 (1): 177- 182
doi: 10.1137/S1052623497318992 |
| 6 | Fletcher R. Unconstrained Optimization. Practical Methods of Optimization: Vol 1. New York: Wiley, 1987 |
| 7 |
Liu Y , Storey C . Efficient generalized conjugate gradient algorithms, part 1:theory. Journal of Optimization Theory and Applications, 1991, 69 (1): 129- 137
doi: 10.1007/BF00940464 |
| 8 |
Gilbert J C , Nocedal J . Global convergence properties of conjugate gradient methods for optimization. SIAM Journal on Optimization, 1992, 2 (1): 21- 42
doi: 10.1137/0802003 |
| 9 | Powell M J D. Nonconvex Minimization Calculations and the Conjugate Gradient Method//Griffiths D F, et al. Numerical Analysis. Berlin: Springer, 1984: 122-141 |
| 10 |
Powell M J D . Convergence properties of algorithms for nonlinear optimization. SIAM Review, 1986, 28 (4): 487- 500
doi: 10.1137/1028154 |
| 11 | Jiang X Z , Jian J B , Song D , et al. An improved Polak-Ribiére-Polyak conjugate gradient method with an efficient restart direction. Computational and Applied Mathematics, 2021, 40 (5): 1- 24 |
| 12 |
Mtagulwa P , Kaelo P . An efficient modified PRP-FR hybrid conjugate gradient method for solving unconstrained optimization problems. Applied Numerical Mathematics, 2019, 145: 111- 120
doi: 10.1016/j.apnum.2019.06.003 |
| 13 | Aminifard Z , Babaie-Kafaki S . A modified descent Polak-Ribiŕe-Polyak conjugate gradient method with global convergence property for nonconvex functions. Calcolo, 2019, 56 (2): 1- 11 |
| 14 |
Liu J K , Feng Y M , Zou L M . A spectral conjugate gradient method for solving large-scale unconstrained optimization. Computers Mathematics with Applications, 2019, 77 (3): 731- 739
doi: 10.1016/j.camwa.2018.10.002 |
| 15 | Dong X L . A modified nonlinear Polak-Ribiére-Polyak conjugate gradient method with sufficient descent property. Calcolo, 2020, 57 (3): 1- 14 |
| 16 |
Dai Z F , Tian B S . Global convergence of some modified PRP nonlinear conjugate gradient methods. Optimization Letters, 2011, 5 (4): 615- 630
doi: 10.1007/s11590-010-0224-8 |
| 17 |
Li M . A three term Polak-Ribiére-Polyak conjugate gradient method close to the memoryless bfgs quasi-newton method. Journal of Industrial Management Optimization, 2020, 16 (1): 245- 260
doi: 10.3934/jimo.2018149 |
| 18 |
Li X L , Shi J J , Dong X L , et al. A new conjugate gradient method based on Quasi-Newton equation for unconstrained optimization. Journal of Computational and Applied Mathematics, 2019, 350: 372- 379
doi: 10.1016/j.cam.2018.10.035 |
| 19 |
Dai Y H , Yuan Y X . A class of globally convergent conjugate gradient methods. Science in China Series A: Mathematics, 2003, 46 (2): 251- 261
doi: 10.1360/03ys9027 |
| 20 |
Barzilai J , Borwein J M . Two-point step size gradient methods. IMA Journal of Numerical Analysis, 1988, 8 (1): 141- 148
doi: 10.1093/imanum/8.1.141 |
| 21 | Luengo F, Raydan M, Glunt W, et al. Preconditioned spectral gradient method for unconstrained optimization problems[R]. Technical Report 96-08, Escuela de Computación, Facultad de Ciencias, Universidad Central de Venezuela, 47002 Caracas 1041-A, Venezuela, 1996 |
| 22 |
Birgin E G , Martínez J M . A spectral conjugate gradient method for unconstrained optimization. Applied Mathematics and Optimization, 2001, 43 (2): 117- 128
doi: 10.1007/s00245-001-0003-0 |
| 23 |
Kou C X , Dai Y H . A modified self-scaling memoryless Broyden-Fletcher-Goldfard-Shanno method for unconstrained optimization. Journal of Optimization Theory and Applications, 2015, 165 (1): 209- 224
doi: 10.1007/s10957-014-0528-4 |
| 24 |
Dai Y H , Kou C X . A nonlinear conjugate gradient algorithm with an optimal property and an improved Wolfe line search. SIAM Journal on Optimization, 2013, 23 (1): 296- 320
doi: 10.1137/100813026 |
| 25 |
Hager W W , Zhang H . A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM Journal on Optimization, 2005, 16 (1): 170- 192
doi: 10.1137/030601880 |
| 26 |
Gould N I M , Orban D , Toint P L . CUTEr and SifDec: A constrained and unconstrained testing environment, revisited. ACM Transactions on Mathematical Software (TOMS), 2003, 29 (4): 373- 394
doi: 10.1145/962437.962439 |
| 27 |
Moré J J , Garbow B S , Hillstrom K E . Testing unconstrained optimization software. ACM Transactions on Mathematical Software, 1981, 7 (1): 17- 41
doi: 10.1145/355934.355936 |
| 28 | Andrei N . An unconstrained optimization test functions collection. Advanced Modeling and Optimization, 2008, 10 (1): 147- 161 |
| 29 |
Dolan E D , Moré J J . Benchmarking optimization software with performance profiles. Mathematical Programming, 2002, 91 (2): 201- 213
doi: 10.1007/s101070100263 |
| [1] | 朱志斌,耿远航. 一个改进的WYL型三项共轭梯度法[J]. 数学物理学报, 2021, 41(6): 1871-1879. |
| [2] | 马国栋. 强Wolfe线搜索下的修正PRP和HS共轭梯度法[J]. 数学物理学报, 2021, 41(3): 837-847. |
| [3] | 李向利,师娟娟,董晓亮. 一类修正的非单调谱共轭梯度法及其在非负矩阵分解中的应用[J]. 数学物理学报, 2018, 38(5): 954-962. |
| [4] | 胡朝明, 万中, 王旭. 一种新的非单调谱共轭梯度算法[J]. 数学物理学报, 2013, 33(1): 78-88. |
| [5] | 时贞军. 精确搜索下的非线性共轭梯度法[J]. 数学物理学报, 2004, 4(6): 675-682. |
|
||