摘要:
设 是不含交换中心投影的von Neumann代数,投影
是不含交换中心投影的von Neumann代数,投影

 使得
使得











 .称可加映射
.称可加映射



 在
在

 Lie可导,若
Lie可导,若




































 .该文证明,若
.该文证明,若

 满足
满足


 ,则
,则 在
在 Lie可导当且仅当存在导子
Lie可导当且仅当存在导子



 和可加映射
和可加映射






 使得
使得

















 ,其中
,其中




















 .特别地,若
.特别地,若 是因子von Neumann代数,
是因子von Neumann代数, 

 满足
满足

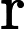




 或
或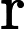




















 ,则可加映射
,则可加映射



 在
在 Lie可导当且仅当
Lie可导当且仅当 有上述形式.
有上述形式.
中图分类号:
杨丽春,安润玲. von Neumann代数上的Lie可导映射[J]. 数学物理学报, 2018, 38(5): 864-872.
Lichun Yang,Runling An. Lie Derivable Maps on von Neumann Algebras[J]. Acta mathematica scientia,Series A, 2018, 38(5): 864-872.