| [1] Gersho A. Adaptive equalization of higuly dispersive channels for date transmisson. BSTJ, 1969, 48: 55--70
[2] Weaver J. Centrosymmetric (cross-symmetric) matrices, their basic properties, eigenvalues and eigenvectors. Am. Math. Monthly, 1985, 92: 711--717
[3] Datta L, Morgera S. On the reducibility of centrosymmetric matrices applications in engineering problems. Ciruits Systems Signal Process, 1989, 8: 71--96
[4] Yuan S F, Wang Q W. Twe special kinds of least squares solutions for the quaternion matrix equation 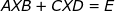 . Electronic Journal of Linear Algebra, 2012, 23: 257--274 . Electronic Journal of Linear Algebra, 2012, 23: 257--274
[5] Wang Q W. A system of matrix equations and a linear matrix equation over arbitrary regular rings with identity. Linear Algebra
Appl. 2004, 384: 43--54
[6] Wang Q W. A system of four matrix equations over von Neumann regular rings and its applications. Acta Math Sin, 2005,
21: 323--334
[7] Wang Q W, Sun J H, Li S Z. Consistency for bi(skew)symmetric solutions to systems of generalized Sylvester equations over a finite central algebra. Linear Algebra Appl. 2002, 353:169--182
[8] Wang Q W, Li C K. Ranks and the least-norm of the general solution to a system of quaternion matrix equations. Linear Algebra Appl,
2009, 430: 1626--1640
[9] Wang Q W, Yu J. On the generalized bi (skew-)symmetric solutions of a linear matrix equation and its Procrust problems. Applied
Mathematics and Computation, 2013, 219: 9872--9884
[10] Wang Q W, Yu G H. The least-square bisymmetric solution to a quaternion matrix equation with applications. Bulletin of the Iranian Mathematical Society, 2013, 39(2): 239--257
[11] Lin Y, Wang Q W. Iterative solution to a system of matrix equations. Abstract and Applied Analysis, 2013, 2013, Article ID 124979
[12] Li N, Wang Q W. Iterative algorithm for solving a class of quaternion matrix equation over the generalized $) -reflexive matrices. Abstract and Applied Analysis, 2013. 2013, Article ID 831656 -reflexive matrices. Abstract and Applied Analysis, 2013. 2013, Article ID 831656
[13] Li N, Wang Q W, Jiang J. An efficient algorithm for the reflexive solution of the quaternion matrix equation  . Journal of Applied Mathematics, 2013, 2013, Article ID 217540 . Journal of Applied Mathematics, 2013, 2013, Article ID 217540
[14] Yin F, Guo K, Huang G X, et al. The inverse eigenproblem with a submatrix constraint and the associated approximation problem for
$) -symmetric matrices. Journal of Computational and Applied Mathematics, 2014, 268: 23--33 -symmetric matrices. Journal of Computational and Applied Mathematics, 2014, 268: 23--33
[15] Yin F, Guo K, Huang G X. An iterative algorithm for the generalized reflexive solutions of the general coupled matrix equations. Journal
of Inequalities and Applications, 2013, 2013(280): 1--15
[16] Yin F, Huang G X. An iterative algorithm for the generalized reflexive solutions of the generalized coupled Sylvester matrix equations. Journal of Applied Mathematics, 2012, 2012, Article ID 152805
[17] Ding J, Liu Y J, Ding F. Iterative solutions to matrix equations of form  . Computers and Mathematics with Applications, . Computers and Mathematics with Applications,
2010, 59 (11): 3500--3507
[18] Xie L, Ding J, Ding F. Gradient based iterative solutions for general linear matrix equations. Computers and Mathematics with
Applications, 2009, 58(7): 1441--1448
[19] Ding F. Hierarchical multi-innovation stochastic gradient algorithm for Hammerstein nonlinear system modeling.
Applied Mathematical Modelling, 2013, 37(4): 1694--1704
[20] Ding F, Chen T. Gradient based iterative algorithms for solving a class of matrix equations. IEEE Trans Automat Control, 2005,
50: 1216--1221
[21] Ding F, Chen T. Iterative least squares solutions of coupled Sylvester matrix equations. Systems Control Lett, 2005,54: 95--107
[22] Ding F, Chen T. Hierarchical gradient-based identification of multivariable discrete-time systems. Automatica, 2005,41: 315--325
[23] Ding F, Chen T. Hierarchical least squares identification methods for multivariable systems. IEEE Trans Automat Control, 2005,
50: 397--402
[24] Ding F, Chen T. On iterative solutions of general coupled matrixequations. SIAM J Control Optim, 2006, 44: 2269--2284
[25] Yin Q X. Construction of real antisymmetric and bi-antisymmetric matrices with prescribed spectrum data. Linear Algebra Appl, 2004, 389: 95--106
[26] Liao A P, Lei Y. Least squares solutions of matrix inverse problem for bisymmetric matrices with a submatrix constraint. Numer Linear Algebra Appl, 2007, 14: 425--444
[27] Bai Z J. The inverse eigen problem of centrosymmetric matrices with a submatrix constraint and its approximation. SIAM J Matrix Anal Appl, 2005,26: 1100--1114
[28] Deift P, Nanda T. On the determination of a tridiagonal matrix from its spectrum and a submatrix. Linear Algebra Appl, 1984, 60: 43--55
[29] Gong L S, Hu X Y, Zhang L. The expansion problem of anti-symmetric matrix under a linear consraint and the optimal approximation. J Comput Appl Math, 2006, 197: 44--52
[30] Zhao L J, Hu X Y, Zhang L. Least squares solutions to for bi-symmetric matrix under a central principal submatrix constraint and the optimal approximation. Linear Algebra Appl, 2008, 428: 871--880 for bi-symmetric matrix under a central principal submatrix constraint and the optimal approximation. Linear Algebra Appl, 2008, 428: 871--880
[31] Wang R S. Functional analysis and optimization theory[D]. Beijing: Beijing Univ of Aeronautics Astronautics, 2003
[32] Kelley C T. Iterative Methods for Linear and Nonlinear Equations. Philadelphia, PA: SIAM, 1995 |