一类具有非等熵 Dusty 气体的两相流模型 Riemann 解的压力消失极限

摘要/Abstract

图/表 5

参考文献 42

Metrics

摘要：

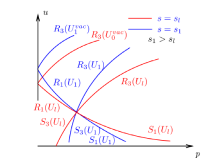
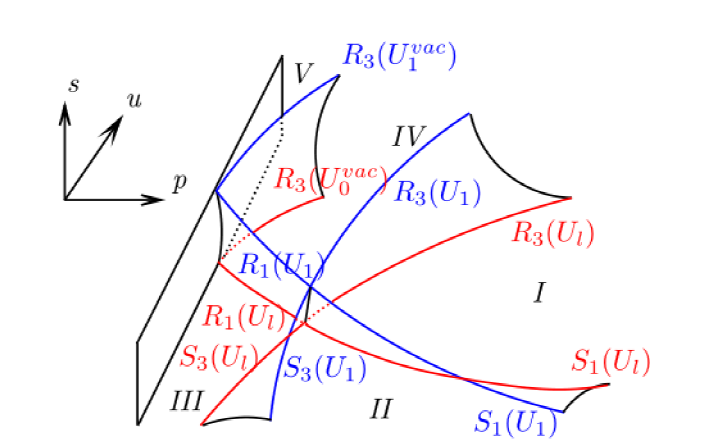
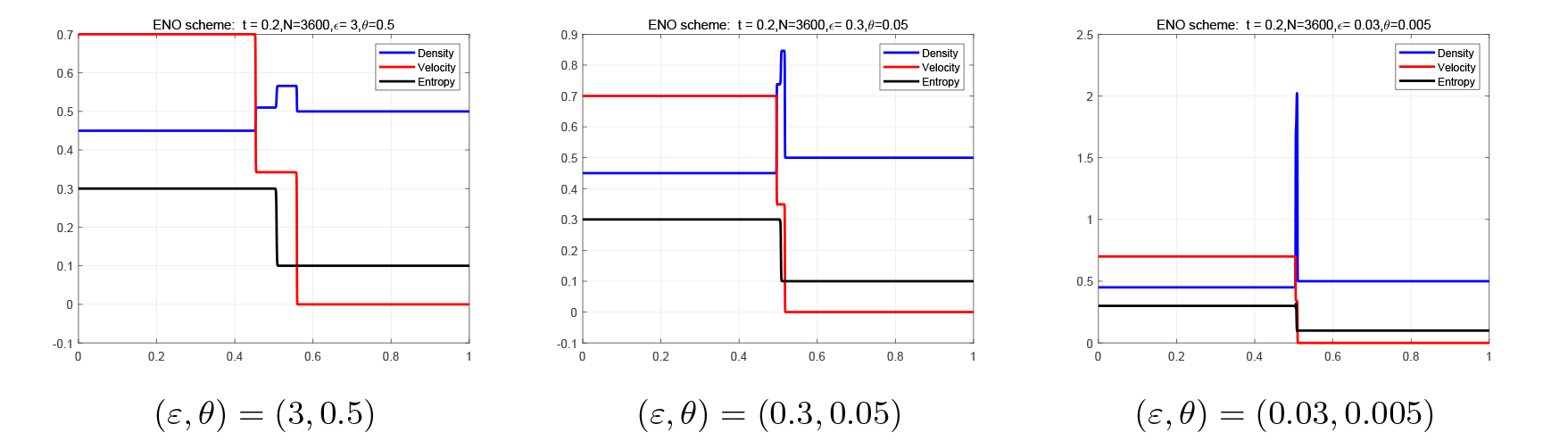
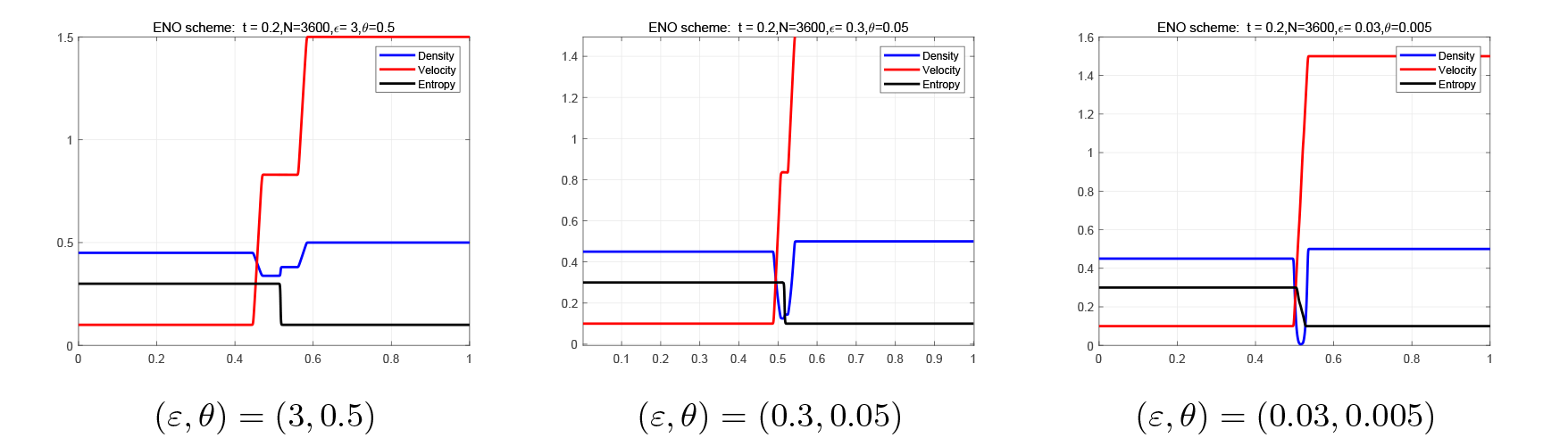
该文研究一类具有非等熵 Dusty 气体的两相流模型 Riemann 解在压力消失时的极限行为. 首先, 针对该模型的黎曼问题, 利用特征分析法得到基本波的表达式并在 $(p, u, s)$ 坐标系中构造了黎曼熵解. 然后, 证明了在压力消失时该模型的黎曼解收敛于带相同初值的一维常压力流体模型的黎曼解. 最后, 对该模型的黎曼解在压力消失过程中 $\delta$ -激波和真空状态的形成进行数值模拟, 验证了上述理论分析的结果.

关键词: 非等熵, 两相流模型, 压力消失极限, 黎曼解, $\delta$ -激波, 真空状态

Abstract:

This paper studies the cavitation and concentration phenomena of the Riemann solutions for a reduced two-phase mixtures model with non-isentropic dusty gas state as the pressure vanishes. Firstly, we construct the Riemann entropy solutions by characteristic analysis method in $(p, u, s)$ coordinate system. Secondly, we conclude that, the pressureless limit of Riemann solutions for the reduced two-phase mixtures model is just the Riemann solutions for the reduced 2-dimensional pressureless gas dynamics model. Finally, we present numerical simulations which are consistent with our theoretical analysis.

Key words: non-isentropic, two-phase mixtures model, pressureless limit, Riemann problem, Delta shock wave, vacuum state

中图分类号:

O175.23

金岱广,何劭弘,吴雨嫣,蒋伟峰. 一类具有非等熵 Dusty 气体的两相流模型 Riemann 解的压力消失极限[J]. 数学物理学报, 2025, 45(2): 371-388.

Daiguang Jin,Shaohong He,Yuyan Wu,Weifeng Jiang. The Vanishing Pressure Limit of Riemann Solutions for a Class of Two-Phase Flow Models with Non-Isentropic Dusty Gases[J]. Acta mathematica scientia,Series A, 2025, 45(2): 371-388.

图1

以 $(p_l, u_l, s_l)$ 和 $(p_l, u_l, s_1)$ 为中心的基本波投影"

图1

图2

图3

$(\varepsilon, \theta)$ 取不同值时方程 (1.1) 和 (5.1) 的黎曼解"

图3

图4

$(\varepsilon, \theta)$ 取不同值时方程 (1.1) 和 (5.2) 的黎曼解"

图4

图5

$(\varepsilon, \theta)=(0.03, 0.005)$ 时方程 (1.1) 和 (5.2) 黎曼解中密度的局部细节"

图5

[1]	Bereux F, Bonnetier E, LeFloch P G. Gas dynamics system: two special cases. SIAM Journal on Mathematical Analysis, 1997, 28(3): 499-515
[2]	Bilicki Z, Kestin J. Physical aspects of the relaxation model in two-phase flow. Proceedings of the Royal Society of London A Mathematical and Physical Sciences, 1990, 428(1875): 379-397
[3]	Minemura K, Uchiyama T. Three-dimensional calculation of air-water two-phase flow in centrifugal pump impeller based on a bubbly flow model. Journal of Fluids Engineering, 1993, 115(4): 776-771
[4]	Sainsaulieu L. Euler system modeling vaporizing sprays. Progress in Astronautics 1993, 152: 280-280
[5]	Zhang T T. The invariant region for the special gas dynamics system. Nonlinear Analysis: Real World Applications, 2017, 38: 68-77
[6]	Frost D L. Heterogeneous/particle-laden blast waves. Shock Waves, 2018, 28(3): 439-449
[7]	Elperin T, Ben-Dor G, Igra O. Head-on collision of normal shock waves in dusty gases. International Journal of Heat and Fluid Flow, 1987, 8(4): 303-312
[8]	Gretler W, Regenfelder R. Similarity solution for variable energy shock waves in a dusty gas under isothermal flow-field condition. Fluid Dynamics Research, 2003, 32(3): Article 69
[9]	Higashino F, Suzuki T. The effect of particles on blast waves in a dusty gas. Zeitschrift für Naturforschung A, 1980, 35(12): 1330-1336
[10]	Guo L H, Sheng W C, Zhang T. The two-dimensional Riemann problem for isentropic Chaplygin gas dynamic system. Communications on Pure and Applied Analysis, 2010, 9: 431-458
[11]	Weinan E, Rykov Y G, Sinai Y G. Generalized variational principles, global weak solutions and behavior with random initial data for systems of conservation laws arising in adhesion particle dynamics. Communications in Mathematical Physics, 1996, 177: 349-380
[12]	Brenier Y, Grenier E. Sticky particles and scalar conservation laws. SIAM journal on numerical analysis, 1998, 35(6): 2317-2328
[13]	Shandarin S F, Zeldovich Y B. The large-scale structure of the universe: Turbulence, intermittency, structures in a self-gravitating medium. Reviews of Modern Physics, 1989, 61(2): 185-220
[14]	Hu J X. One-dimensional Riemann problem for equations of constant pressure fluid dynamics with measure solutions by the viscosity method. Acta Applicandae Mathematica, 1999, 55: 209-229
[15]	Korchinski D J. Solution of a Riemann Problem for a 2 x 2 System of Conservation Laws Possessing No Classical Weak Solution. New York: Adelphi University, 1997
[16]	Tan D C, Zhang T. Two-dimensional Riemann problem for a hyperbolic system of nonlinear conservation laws. Journal of Differential Equations, 1994, 111: 203-254; 255-282
[17]	Tan D C, Zhang T, Chang T, Zheng Y X. Delta-shock waves as limits of vanishing viscosity for hyperbolic systems of conservation laws. Journal of Differential Equations, 1994, 112(1): 1-32
[18]	Yang H C, Zhang Y Y. New developments of delta shock waves and its applications in systems of conservation laws. Journal of Differential Equations, 2012, 252(11): 5951-5993
[19]	李华惠, 邵志强. 压力消失时具有广义 Chaplygin 气体的 Aw-Rascle 交通模型 Riemann 解的极限. 数学物理学报, 2017, 37A(5): 917-930
	Li H H, Shao Z Q. Limit of Riemann solution for Aw-Raschle traffic model with generalized Chaplygin gas when pressure disappears. Acta Math Sci, 2017, 37A(5): 917-930
[20]	邵志强. 一维具有阻尼和摩擦项的可压缩流体欧拉方程组当压力消失时黎曼解的极限. 数学物理学报, 2022, 42A(4): 1150-1172
	Shao Z Q. Limit of Riemann solution for one-dimensional compressible fluid Euler equations with damping and friction terms when pressure disappears. Acta Math Sci, 2022, 42A(4): 1150-1172
[21]	Yang H C. Riemann problems for a class of coupled hyperbolic systems of conservation laws. Journal of Differential Equations, 1999, 159(2): 447-484
[22]	Sheng W C, Zhang T. The Riemann Problem for the Transportation Equations in Gas Dynamics. American Mathematical Society, 1999
[23]	Ding X, Wang Z. Existence and uniqueness of discontinuous solutions defined by Lebesgue-Stieltjes integral. Sci China Ser A, 1996, 39(8): 807-819
[24]	Li J Q. Note on the compressible Euler equations with zero temperature. Applied Mathematics Letters, 2001, 14(4): 519-523
[25]	Chen G Q, Liu H L. Formation of $\delta$ -shocks and vacuum states in the vanishing pressure limit of solutions to the Euler equations for isentropic fluids. SIAM Journal on Mathematical Analysis, 2003, 34(4): 925-938
[26]	Sheng W C, Wang G J, Yin G. Delta wave and vacuum state for generalized Chaplygin gas dynamics system as pressure vanishes. Nonlinear Analysis: Real World Applications, 2015, 22: 115-128
[27]	Shen C, Sun M N. Formation of delta shocks and vacuum states in the vanishing pressure limit of Riemann solutions to the perturbed Aw-Rascle model. Journal of Differential Equations, 2010, 249(12): 3024-3051
[28]	Yang H C, Wang J H. Delta-shocks and vacuum states in the vanishing pressure limit of solutions to the isentropic Euler equations for modified Chaplygin gas. Journal of Mathematical Analysis and Applications, 2014, 413(2): 800-820
[29]	Zhang Q L. The vanishing pressure limit of solutions to the simplified Euler equations for isentropic fluids. Annals of Applied Mathematics, 2012, 28(1): 115-126
[30]	Zhang Y, Fan S, Zhang Y Y. Concentration and cavitation in the vanishing pressure limit of solutions to a 3 $\times$ 3 generalized Chaplygin gas equations. Mathematical Modelling of Natural Phenomena, 2022, 17: Article 10
[31]	Shen C. The singular limits of solutions to the Riemann problem for the liquid-gas two-phase isentropic flow model. Journal of Mathematical Physics, 2020, 61(8): Article 081502
[32]	Song Y T, Guo L H. General limiting behavior of Riemann solutions to the non-isentropic Euler equations for modified Chaplygin gas. Journal of Mathematical Physics, 2020, 61(4): Article 041506
[33]	Song Y T, Guo L H. Behavior of Riemann solutions of extended chaplygin gas under the limiting condition. Acta Applicandae Mathematicae, 2021, 174: 1-17
[34]	Zhang Y, Pang Y C, Wang J H. Concentration and cavitation in the vanishing pressure limit of solutions to the generalized Chaplygin Euler equations of compressible fluid flow. European Journal of Mechanics-B/Fluids, 2019, 78: 252-262
[35]	Kipgen L, Singh R. $\delta$ -shocks and vacuum states in the Riemann problem for isothermal van der Waals dusty gas under the flux approximation. Physics of Fluids, 2023, 35(1): Article 016116
[36]	Yang H C, Wang J H. Concentration in vanishing pressure limit of solutions to the modified Chaplygin gas equations. Journal of Mathematical Physics, 2016, 57(11): Article 111504
[37]	Chaturvedi R K, Singh L. The phenomena of concentration and cavitation in the Riemann solution for the isentropic zero-pressure dusty gasdynamics. Journal of Mathematical Physics, 2021, 62(3): Article 033101
[38]	Lei Z T, Shao Z Q. Concentration and cavitation in the vanishing pressure limit of solutions to the relativistic Euler equations with the logarithmic equation of state. Journal of Mathematical Physics, 2023, 64(7): Article 071507
[39]	Jiang W F, Zhang Y, Li T, Chen T T. The cavitation and concentration of Riemann solutions for the isentropic Euler equations with isothermal dusty gas. Nonlinear Analysis: Real World Applications, 2023, 71: Article 103761
[40]	Pang Y C, Ge J J, Liu Z Z, Hu M. The Riemann problem for one-dimensional isentropic flow of a mixture of a non-ideal gas with small solid particles. Results in Physics, 2019, 15: Article 102587
[41]	Chen G Q, Liu H L. Concentration and cavitation in the vanishing pressure limit of solutions to the Euler equations for nonisentropic fluids. Physica D: Nonlinear Phenomena, 2004, 189(1/2): 141-165
[42]	Jiang W F, Jin D G, Li T, Chen T T. The singular limits of the Riemann solutions as pressure vanishes for a reduced two-phase mixtures model with non-isentropic gas state. Journal of Mathematical Physics, 2024, 65(7): Article 071503

Just accepted

Online first

Just accepted

Online first

Viewed

Full text

	From	local

	Times	63
	Rate	100%

Abstract

Just accepted	Online first	Issue

0	0	34

Cited

Shared

Discussed