数学物理学报 ›› 2024, Vol. 44 ›› Issue (5): 1242-1282.
阶跃初值条件解的完全分类: 流体力学中广义 Gardner 方程的分析与数值验证
- 太原理工大学数学学院 太原 030024
-
收稿日期:2023-10-27修回日期:2024-04-29出版日期:2024-10-26发布日期:2024-10-16 -
通讯作者:*郝惠琴, E-mail:math0351@sina.com -
作者简介:张岩, E-mail:z1093767571@163.com ;|郭睿, E-mail:gr81@sina.com -
基金资助:国家自然科学基金(11905155);山西省留学人员科学活动基金(20220008)
The Complete Classification of Solutions to the Step Initial Condition: Analysis and Numerical Verification for the Generalized Gardner Equation in Fluid Mechanics
Zhang Yan( ),Hao Huiqin*(
),Hao Huiqin*( ),Guo Rui(
),Guo Rui( )
)
- School of Mathematics, Taiyuan University of Technology, Taiyuan 030024
-
Received:2023-10-27Revised:2024-04-29Online:2024-10-26Published:2024-10-16 -
Supported by:NSFC(11905155);Scientific Activities of Selected Returned Overseas Scholars in Shanxi Province(20220008)
摘要:
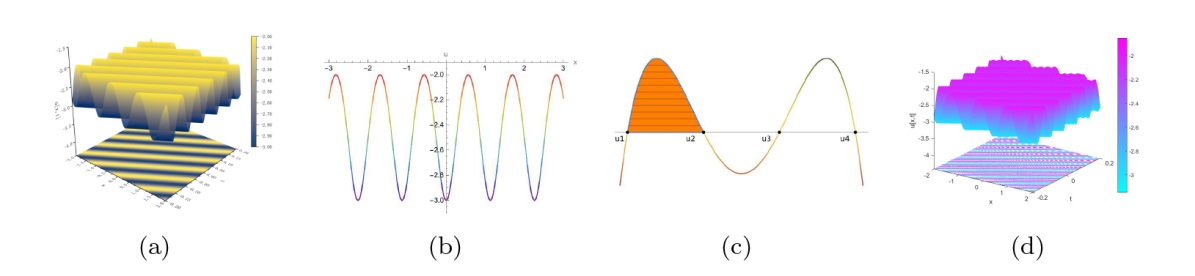
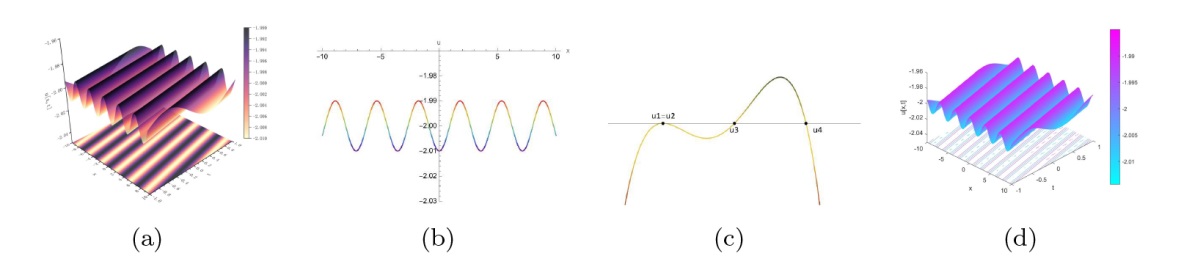
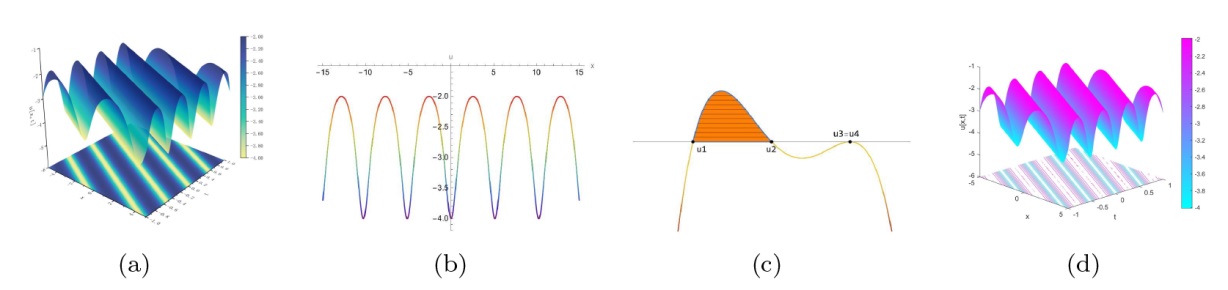
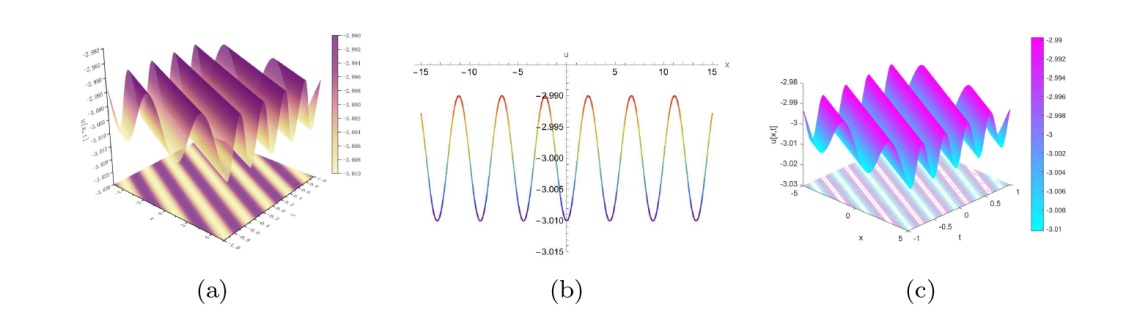
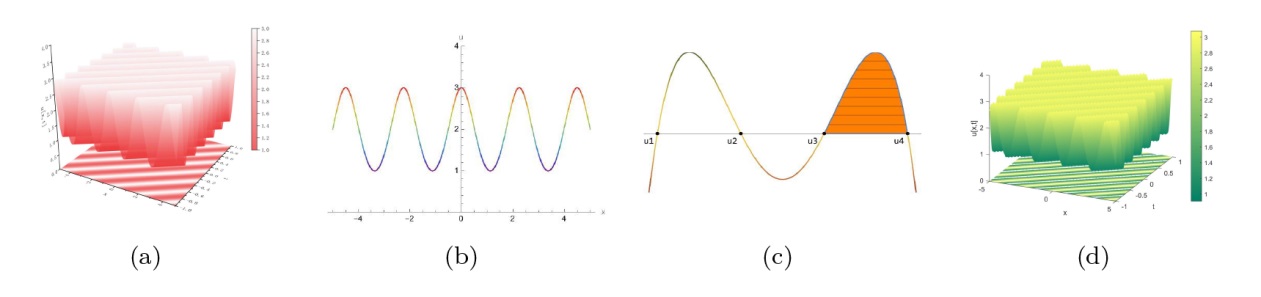
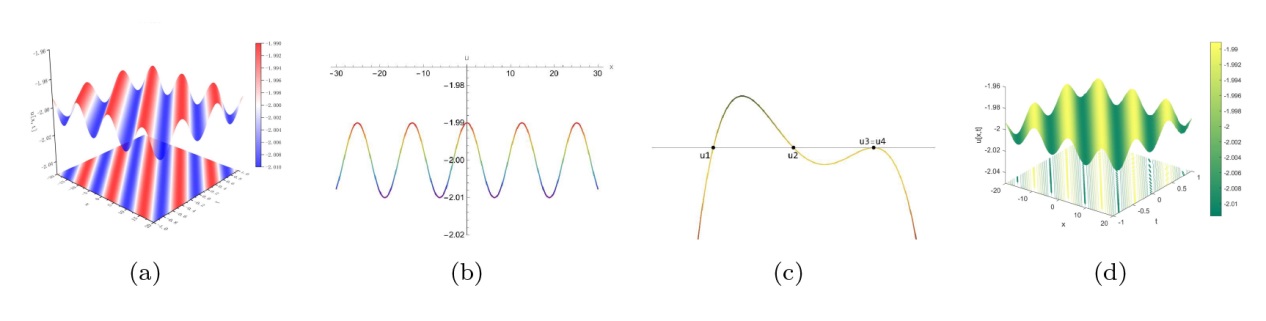
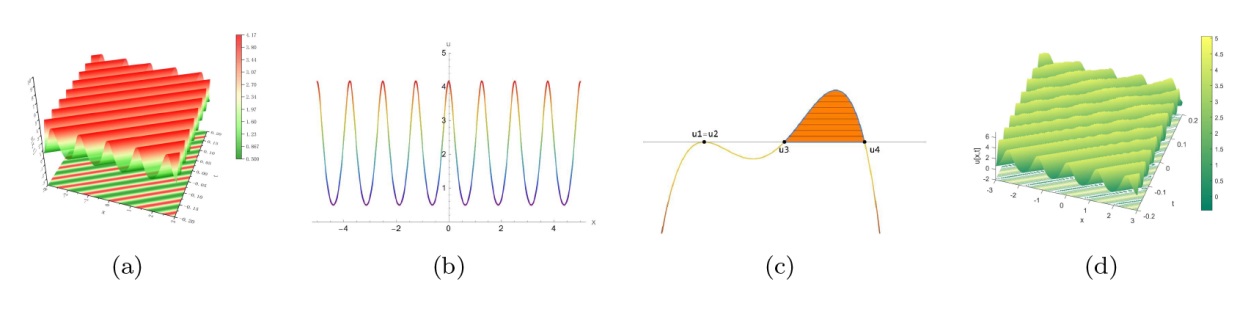
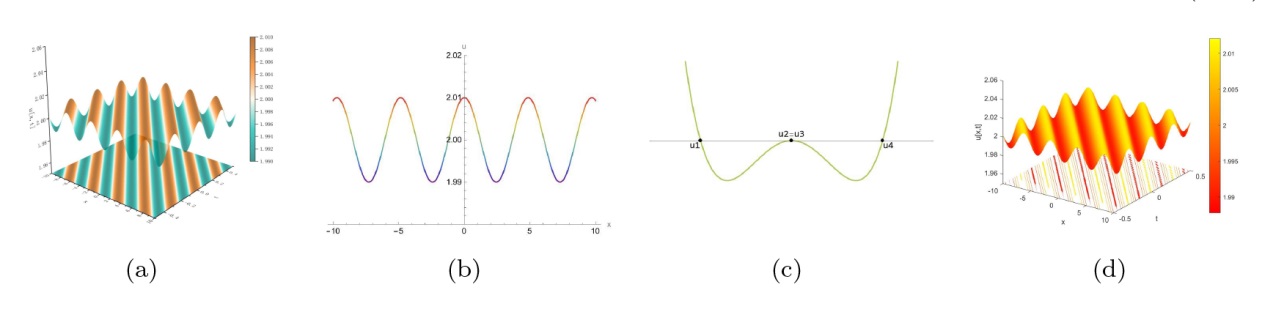
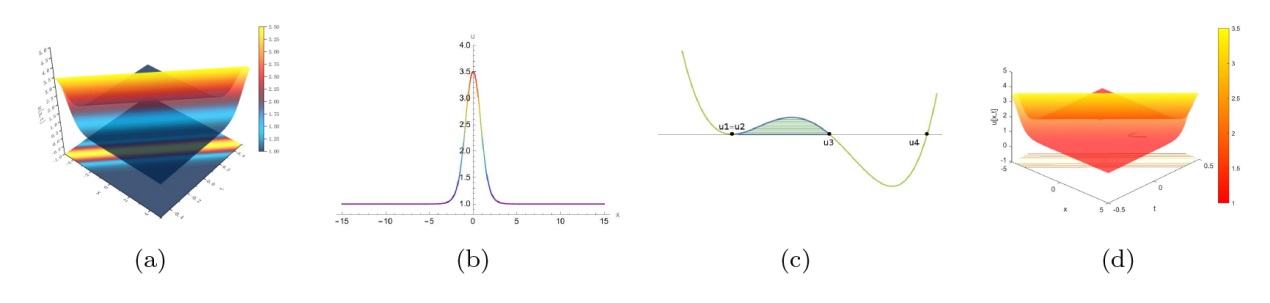
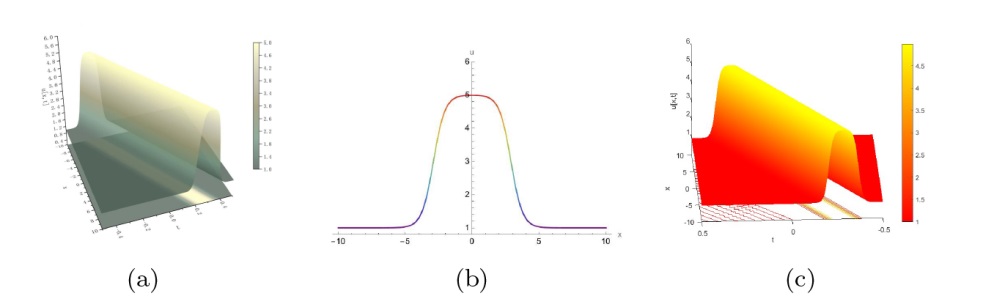
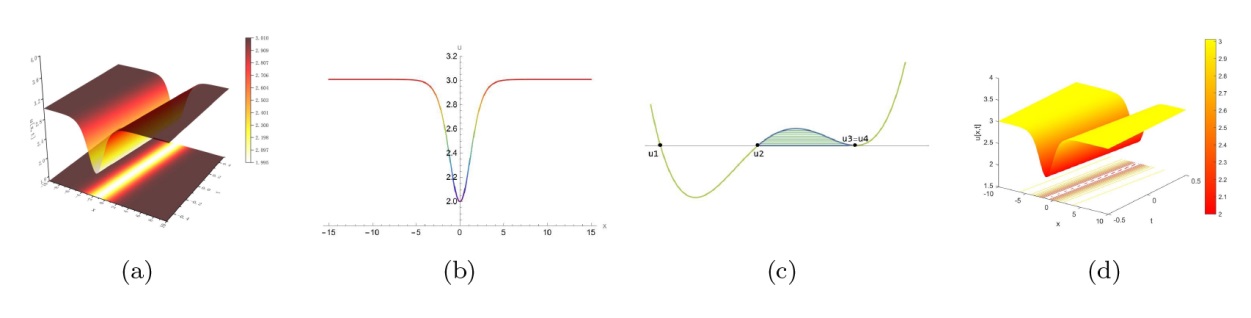
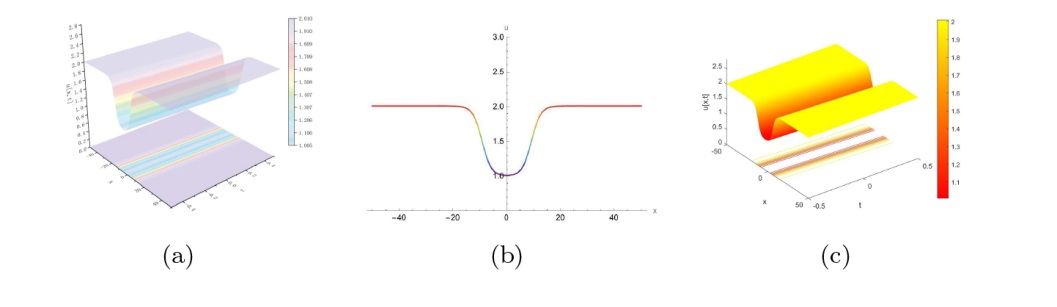
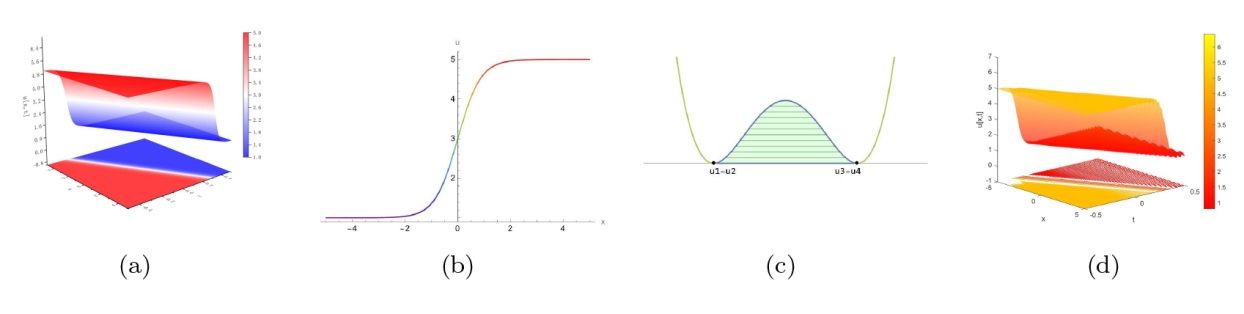
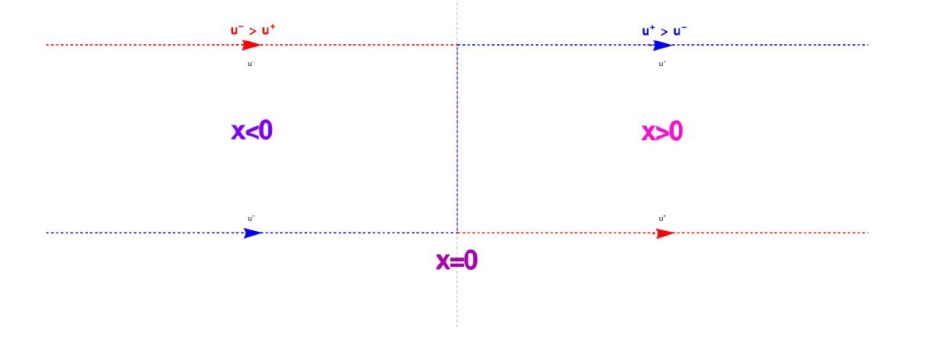
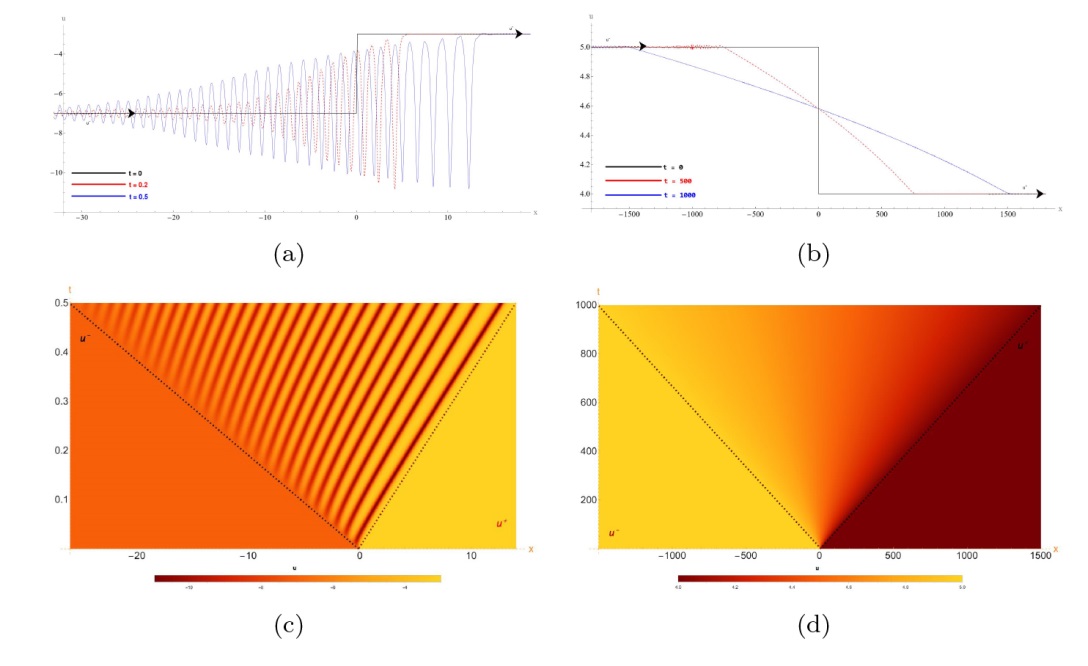
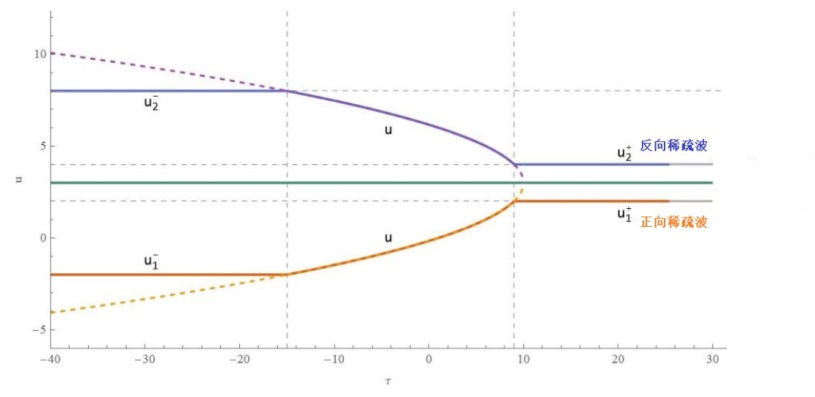
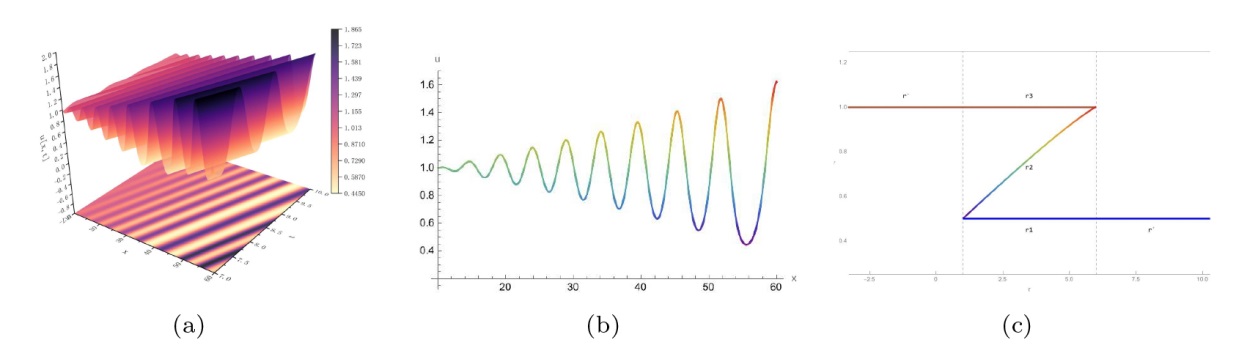
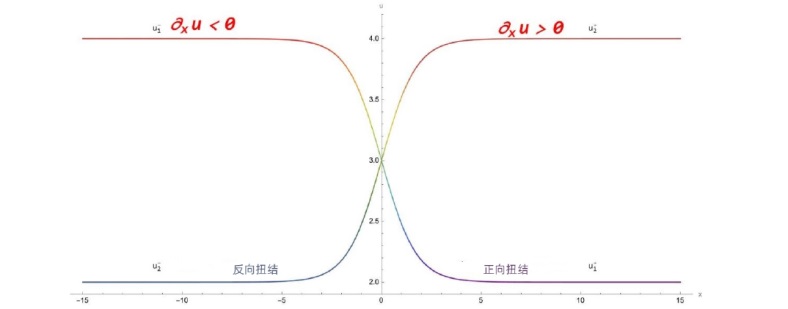
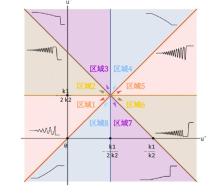
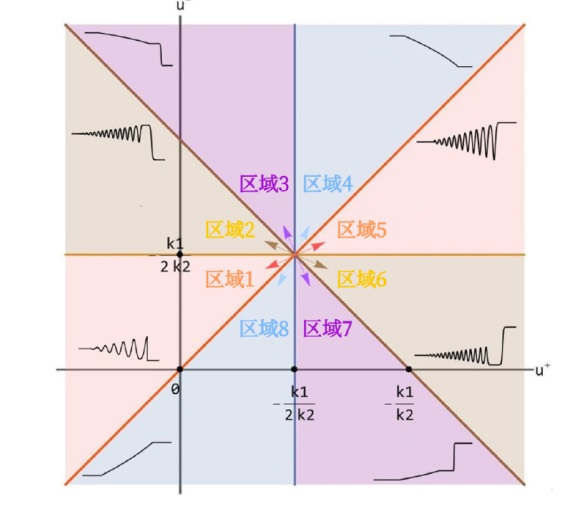
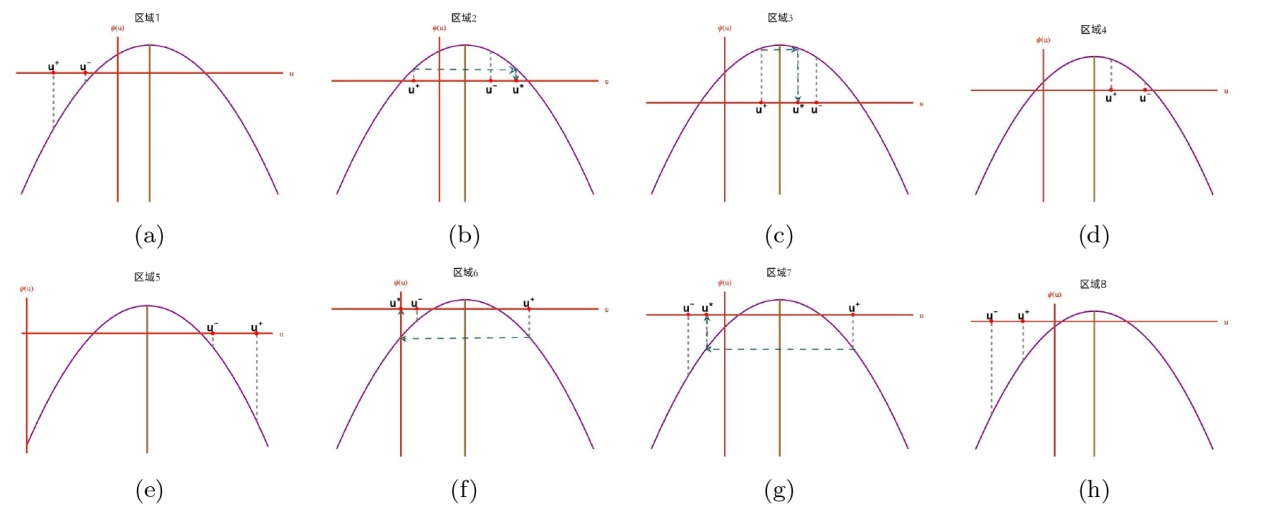
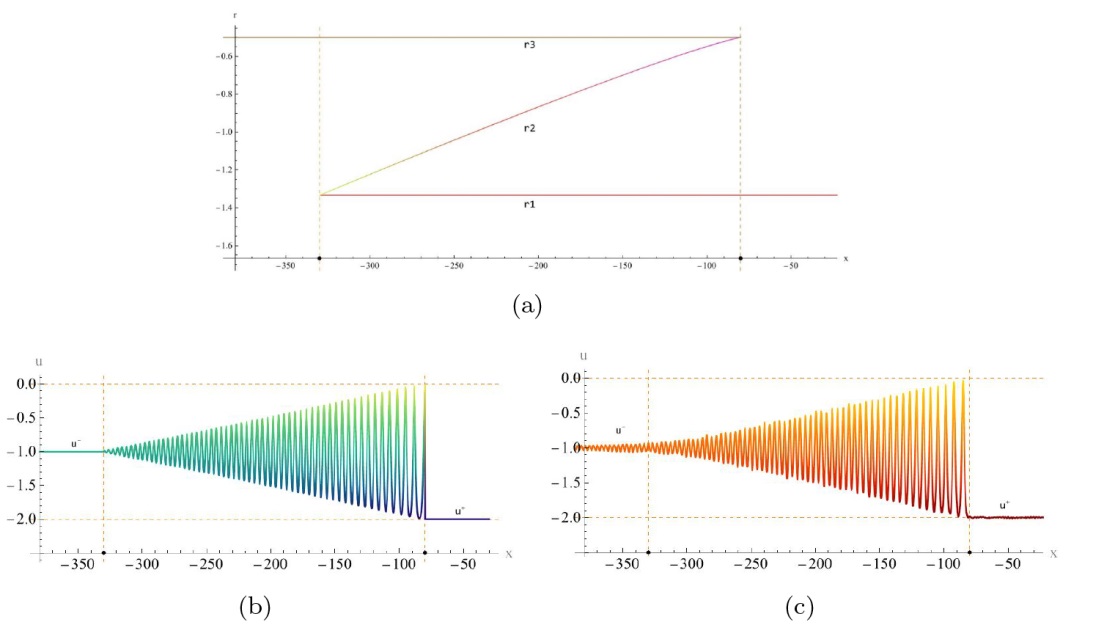
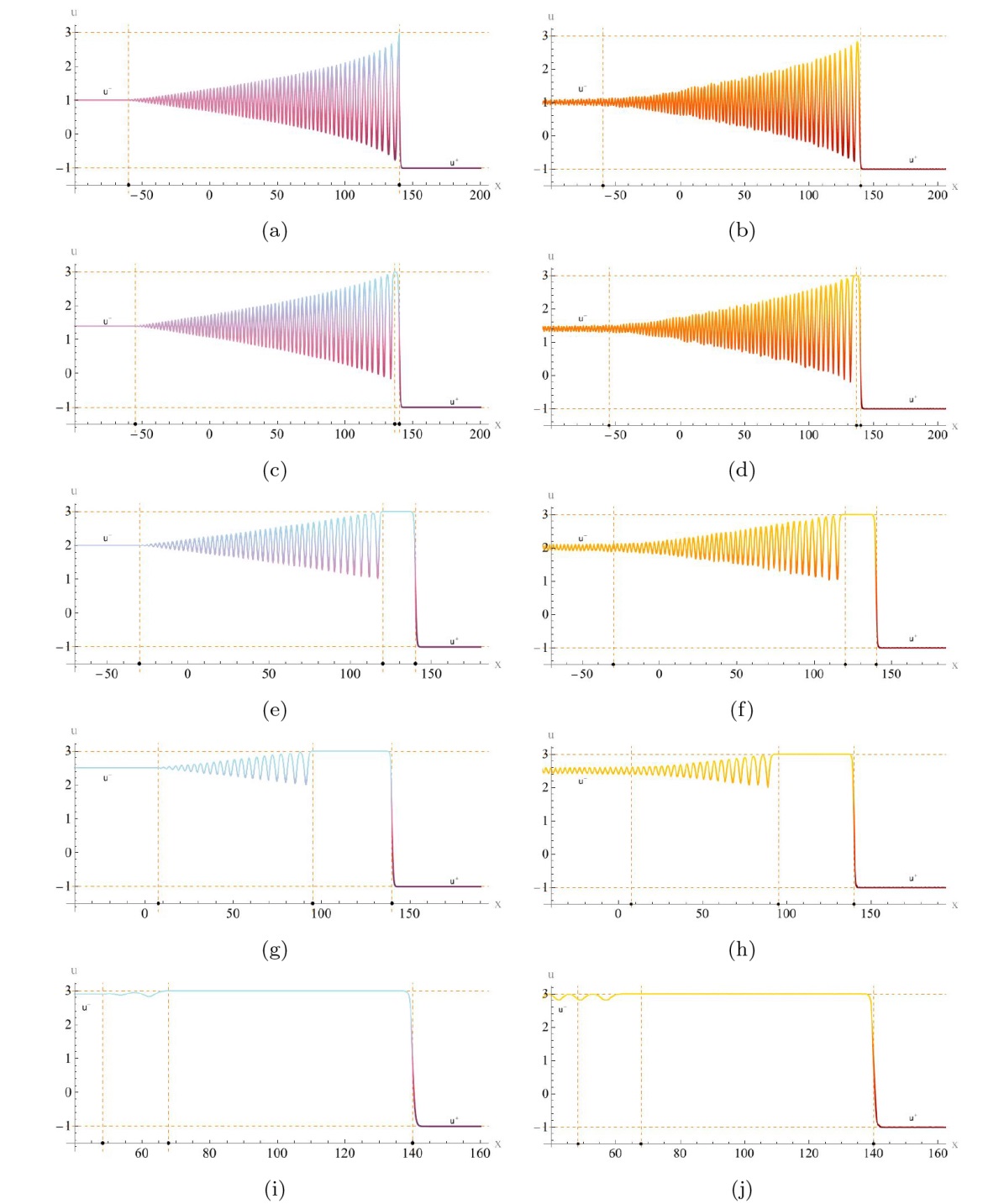
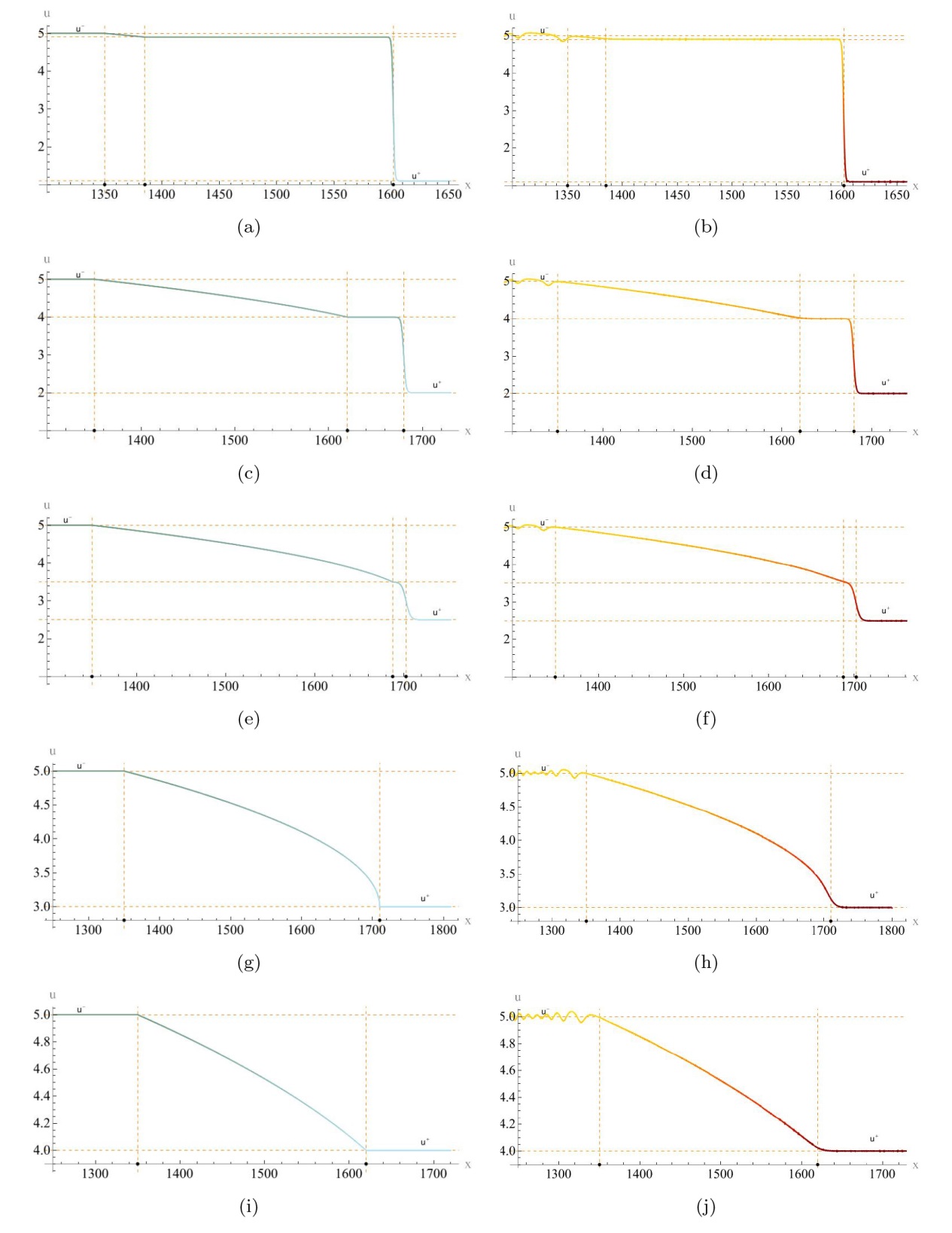
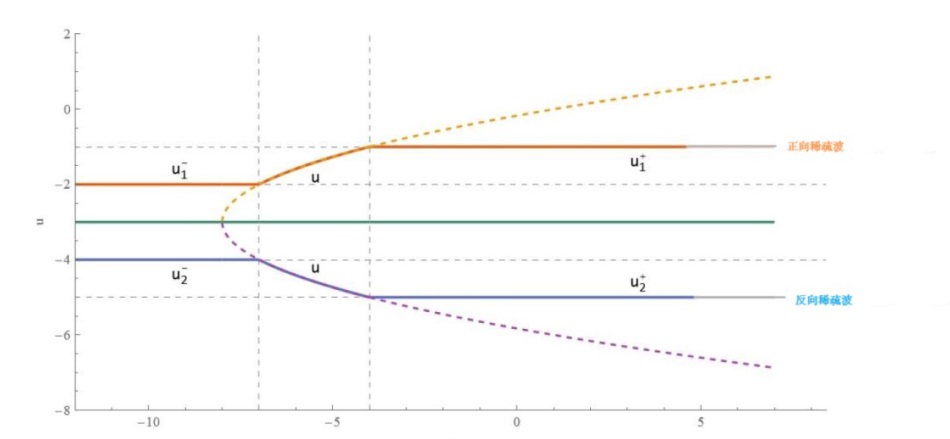
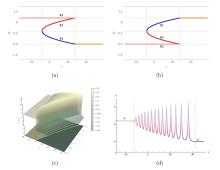
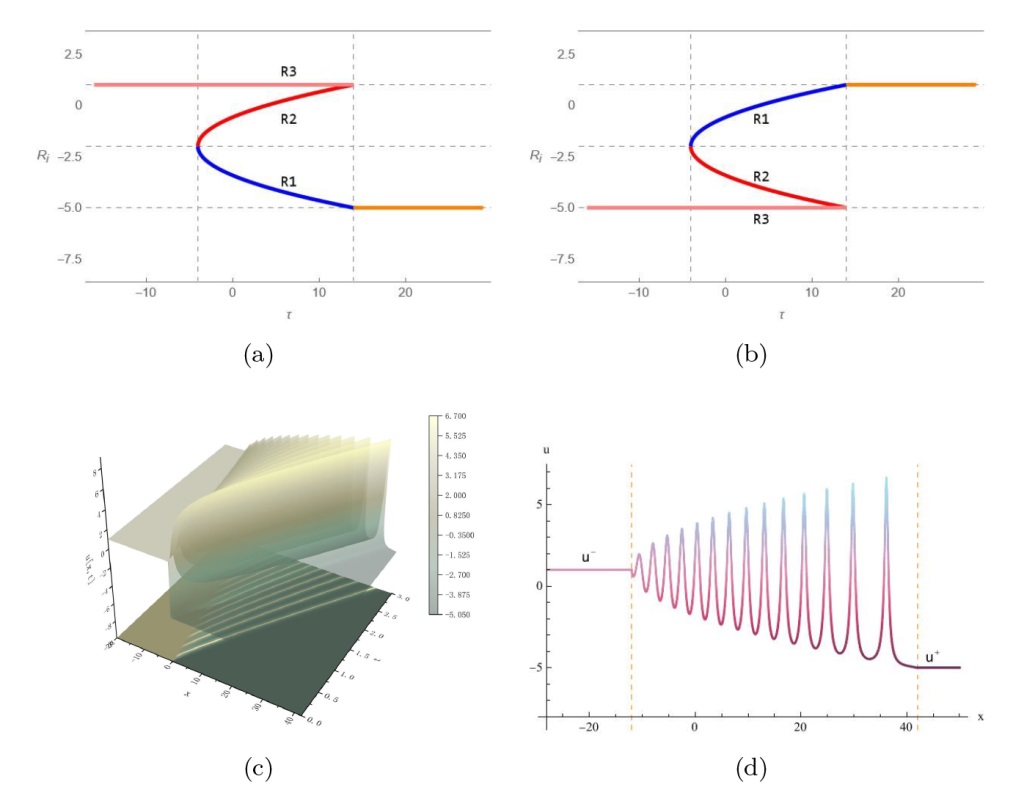
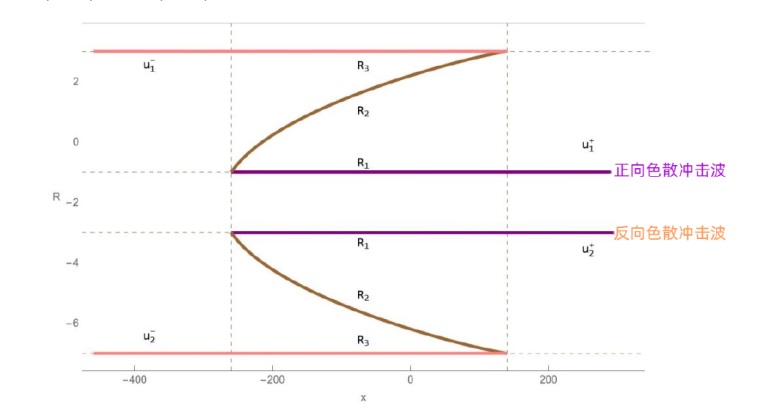
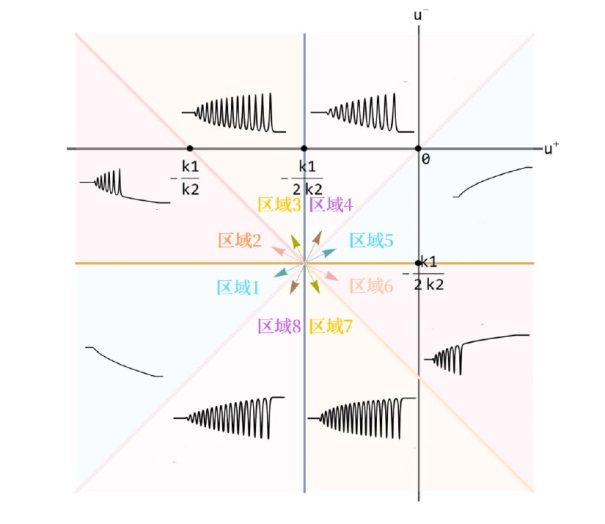
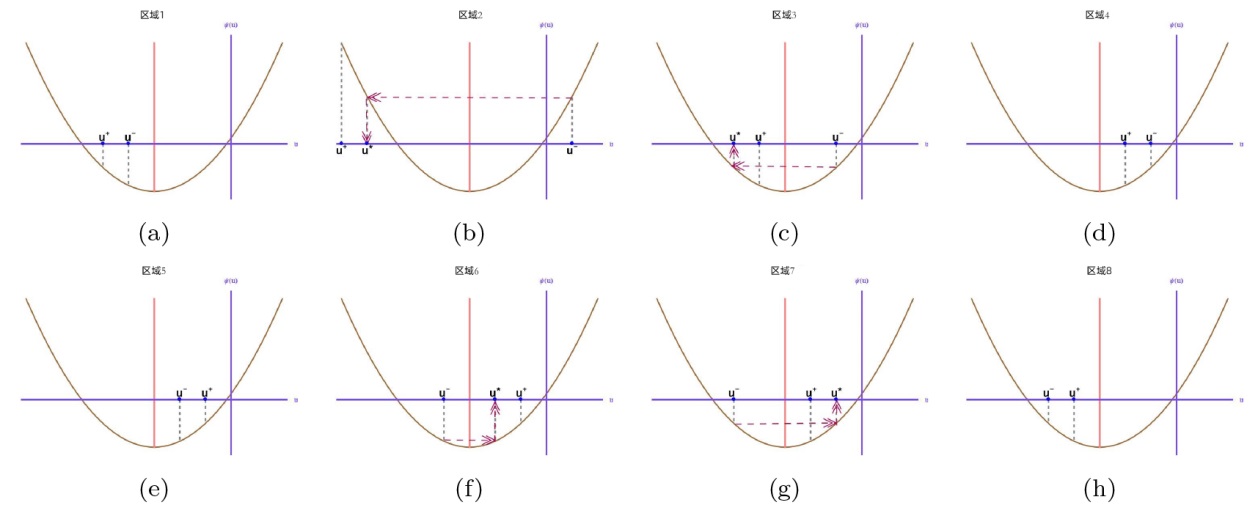
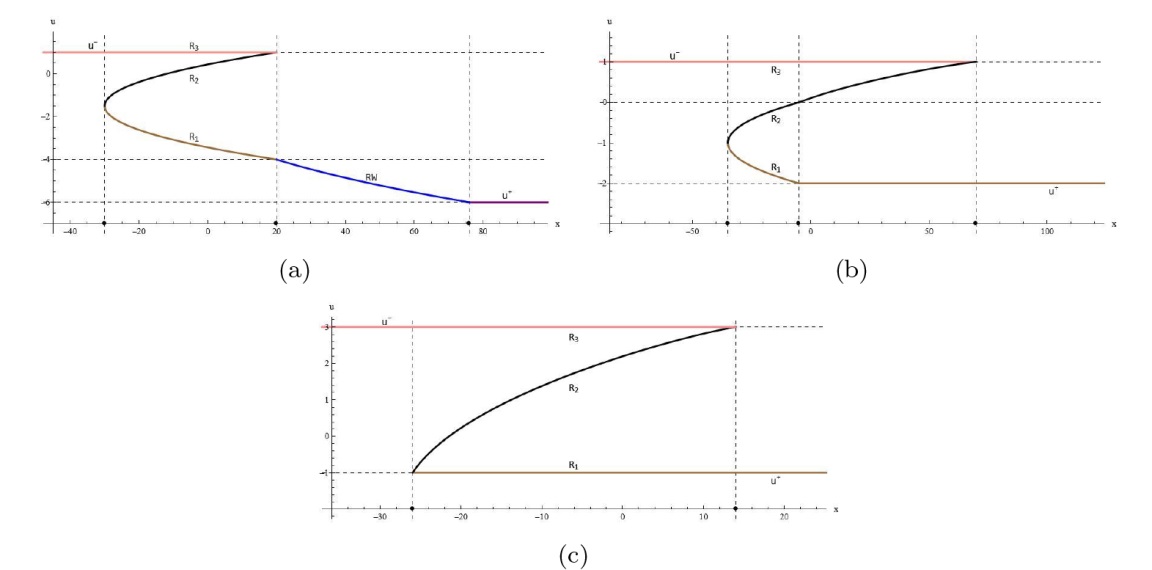
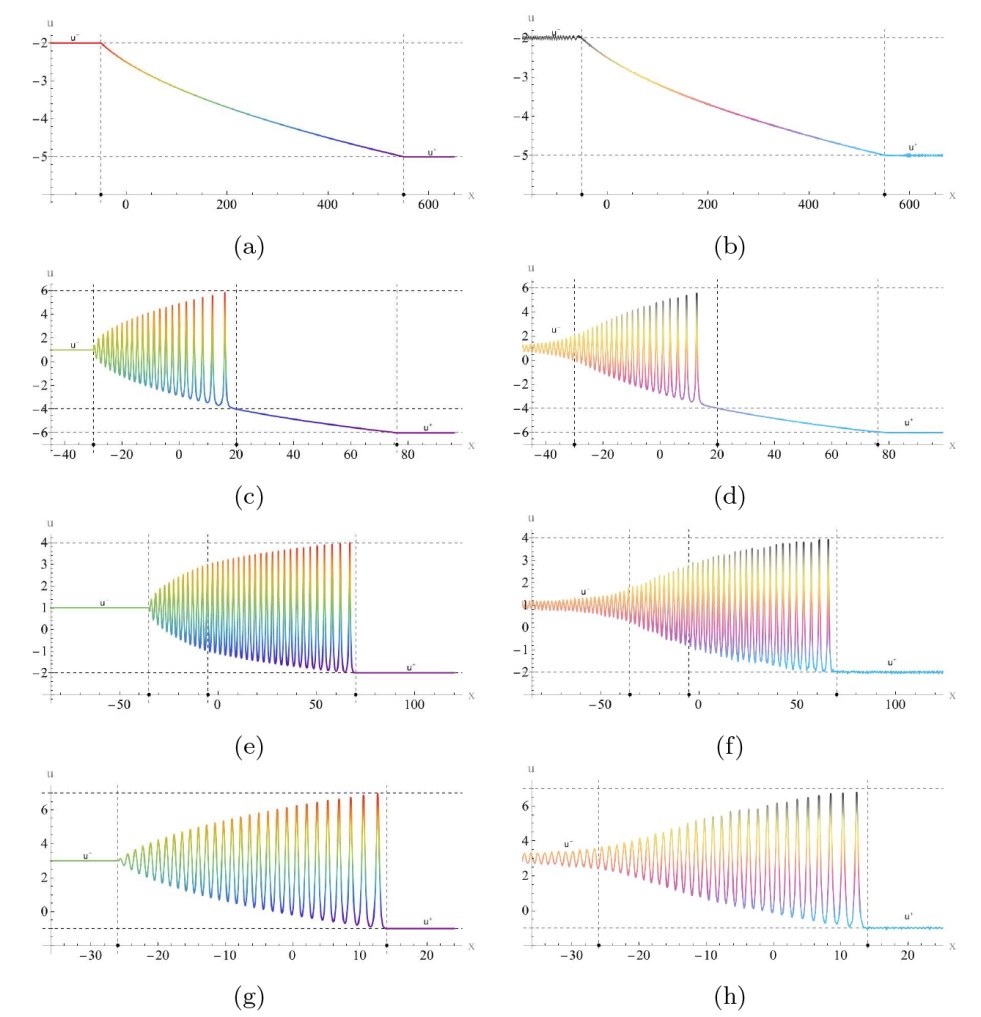
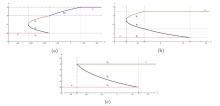
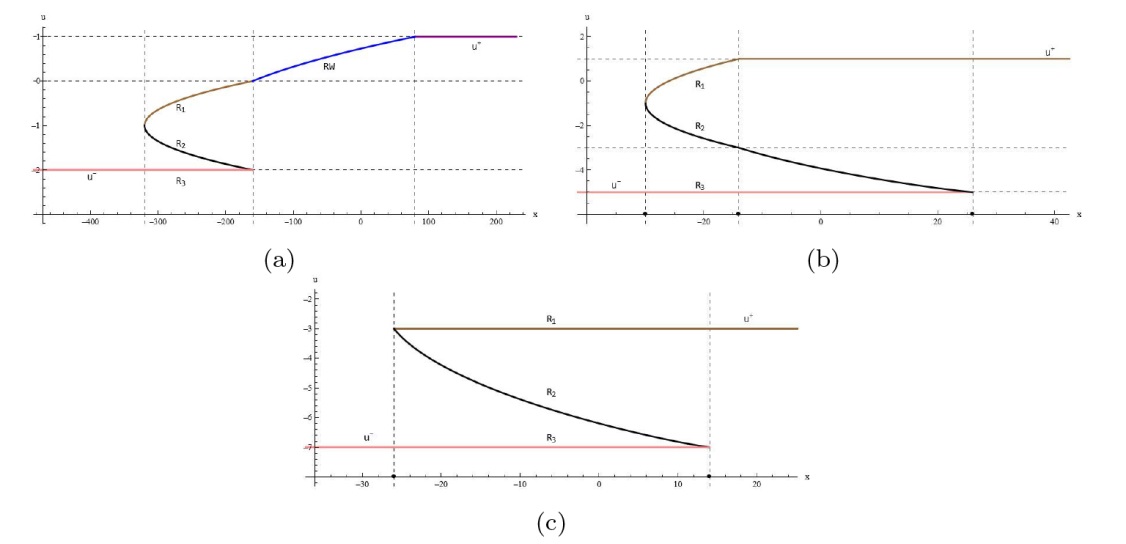
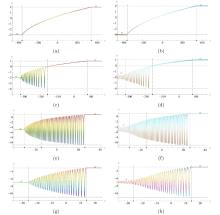
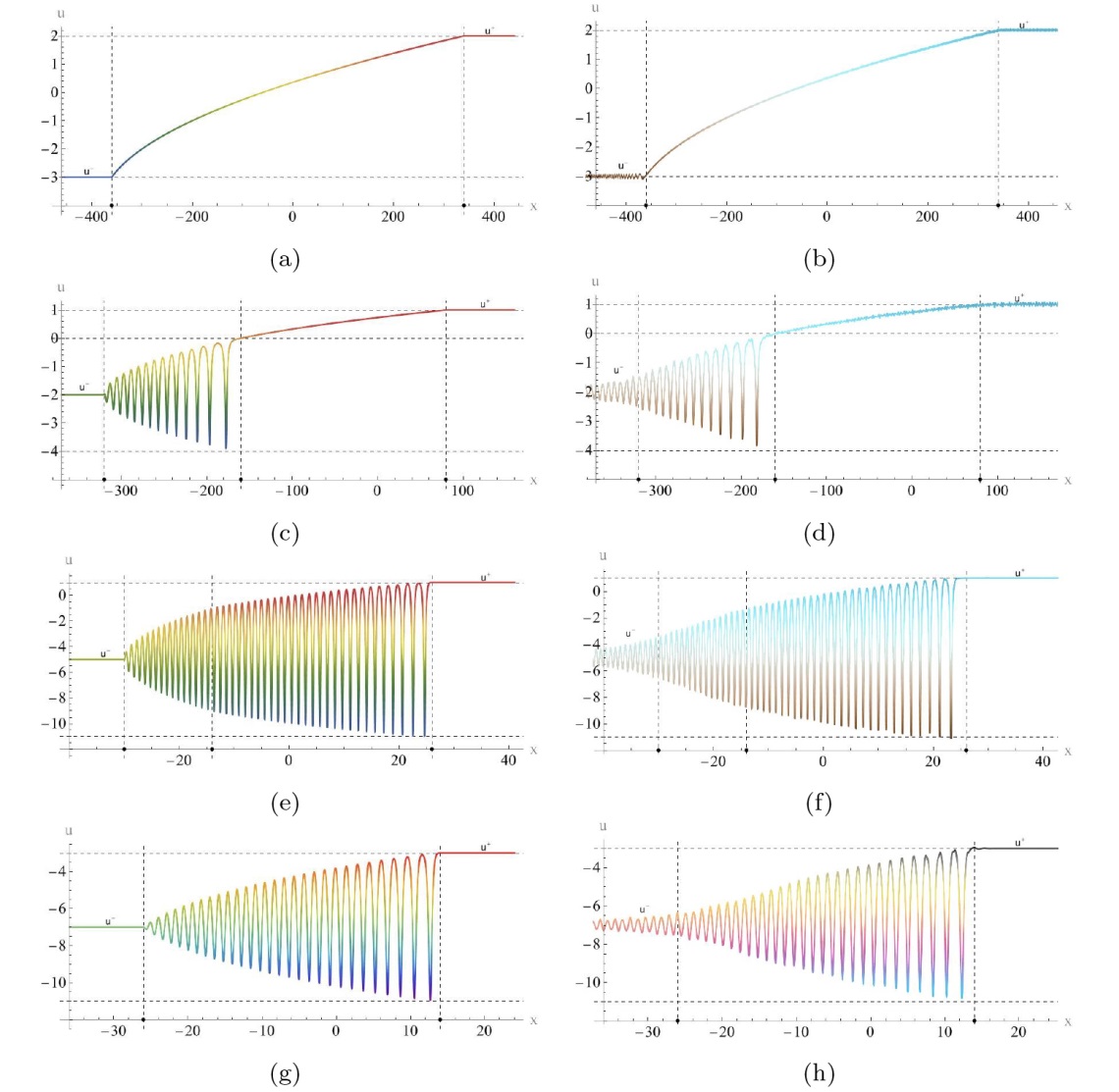
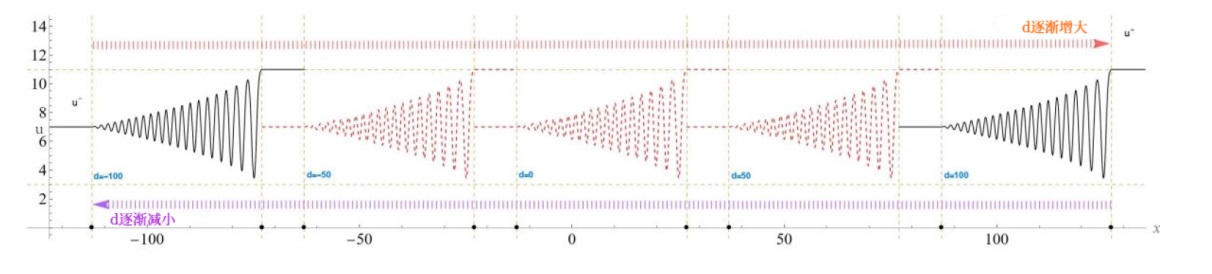
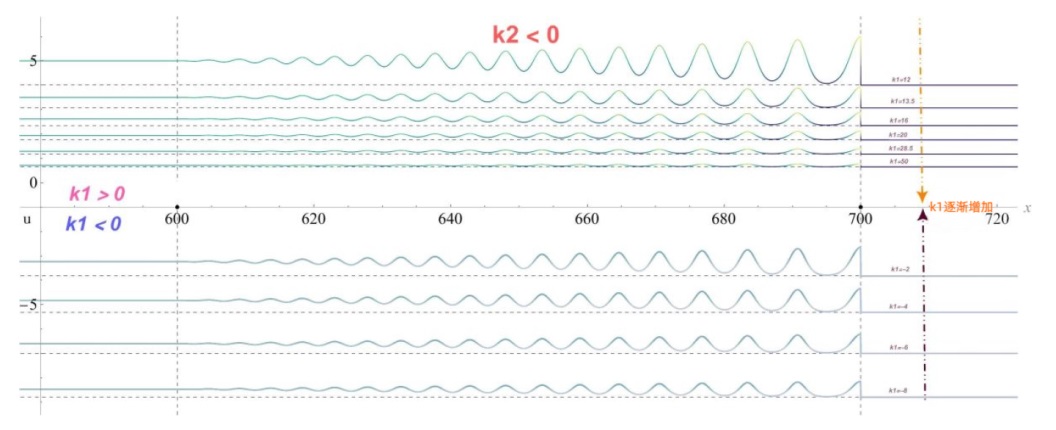
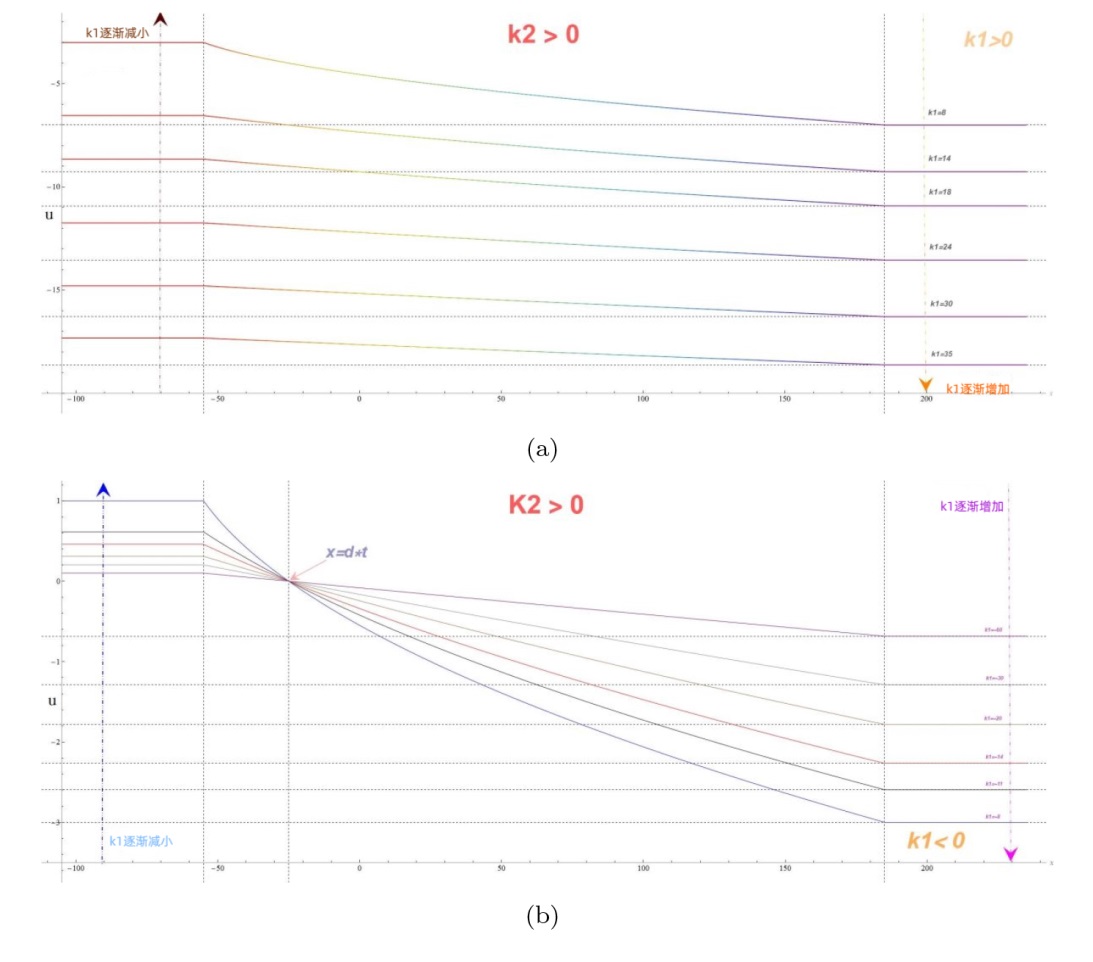
该文中, 通过 Whitham 调制理论研究了广义 Gardner 方程的初始不连续性的演化, 该方程可以描述地形上分层流体的跨临界流动. 首先, 通过雅可比椭圆函数表示的周期波推导出不同极限情况下的线性谐波, 孤子和非线性三角波. 随后通过有限间隙积分方法得到了基于黎曼不变量的 Whitham 特征速度与调制系统. 由于广义 Gardner 方程的调制系统既不是严格的椭圆型也不是严格的双曲型, 这使得与 KdV 方程相比, 不同区域当中的动力学演化行为更加多样化. 此外, 对正负三次非线性项情况下的所有波结构进行了完整的分类, 包括色散冲击波, 稀疏波, 三角冲击波, 扭结及其组合波结构, 并通过数值模拟验证了结果的正确性. 最后分析了一定条件下线性项和非线性项的系数对阶跃初值问题的影响.
中图分类号:
- O322
引用本文
张岩, 郝惠琴, 郭睿. 阶跃初值条件解的完全分类: 流体力学中广义 Gardner 方程的分析与数值验证[J]. 数学物理学报, 2024, 44(5): 1242-1282.
Zhang Yan, Hao Huiqin, Guo Rui. The Complete Classification of Solutions to the Step Initial Condition: Analysis and Numerical Verification for the Generalized Gardner Equation in Fluid Mechanics[J]. Acta mathematica scientia,Series A, 2024, 44(5): 1242-1282.
使用本文
| [1] | Infeld E, Rowlands G. Nonlinear Waves, Solitons and Chaos. New York: Cambridge University Press, 1990 |
| [2] | Ablowitz M J, Clarkson P A. Solitons, Nonlinear Evolution Equations and Inverse Scattering. New York: Cambridge University Press, 1991 |
| [3] | Kevrekidis P G, Frantzeskakis D J, Carretero-González R. Emergent Nonlinear Phenomena in Bose-Einstein Condensates. New York: Springer, 2008 |
| [4] | Korteweg D J, De Vries G. On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Phil Mag, 1895, 5(39): 422-443 |
| [5] | Miura R M. Korteweg-de Vries equation and generalizations. I. A remarkable explicit nonlinear transformation. J Math Phys, 1968, 9(8): 1202-1204 |
| [6] | Miura R M, Gardner C S, Kruskal M D. Korteweg-de Vries equation and generalizations. II. Existence of conservation laws and constants of motion. J Math Phys, 1968, 9(8): 1204-1209 |
| [7] | Su C H, Gardner C S. Korteweg-de Vries equation and generalizations. III. Derivation of the Korteweg-de Vries equation and Burgers equation. J Math Phys, 1969, 10(3): 536-539 |
| [8] | Gardner C S. Korteweg-de Vries equation and generalizations. IV. The Korteweg-de Vries equation as a Hamiltonian system. J Math Phys, 1971, 12(8): 1548-1551 |
| [9] | Mishra M K, Chhabra R S, Sharma S R. Obliquely propagating ion-acoustic solitons in a multi-component magnetized plasma with negative ions. J Plasma Phys, 1994, 52(3): 409-429 |
| [10] | Horii Z. Formulation of the Korteweg-de Vries and the Burgers equations expressing mass transports from the generalized Kawasaki-Ohta equation. Phys Lett A, 2002, 306: 45-51 |
| [11] |
Apela J R, Ostrovsky L A, Stepanyants Y A, et al. Internal solitons in the ocean and their effect on underwater sound. J Acoust Soc Am, 2007, 121(2): 695-722
pmid: 17348494 |
| [12] | Leblond H, Grelu P, Mihalache D. Models for supercontinuum generation beyond the slowly-varying-envelope approximation. Phys Rev A, 2014, 90: 053816 |
| [13] | Ralph E A, Pratt L. Predicting eddy detachment for an equivalent barotropic thin jet. J Nonlinear Sci, 1994, 4: 355-374 |
| [14] | Das G C, Karmakar B. Nonlinear ion-acoustic waves in multicomponent plasmas. Can J Phys, 1988, 66(1): 79-81 |
| [15] | Chow K W, Grimshaw R H J, Ding E. Interactions of breathers and solitons in the extended Korteweg-de Vries equation. Wave Motion, 2005, 43(2): 158-166 |
| [16] | Bokaeeyan M, Ankiewicz A, Akhmediev N. Bright and dark rogue internal waves: The Gardner equation approach. Phys Rev E, 2019, 99(6): 062224 |
| [17] | Baldwin D, Goktas U, Hereman W, et al. Symbolic computation of exact solutions in hyperbolic and elliptic functions for nonlinear PDEs. J Symb Comput, 2004, 37: 669-705 |
| [18] | Demler E, Maltsev A. Semiclassical solitons in strongly correlated systems of ultracold bosonic atoms in optical lattices. Ann Phys, 2011, 326(7): 1775-1805 |
| [19] | Demiray S T, Bulut H. New exact solutions for generalized Gardner equation. Kuwait J Sci, 2017, 44(1): 1-8 |
| [20] | Grimshaw R. Environmental Stratified Flows. New York: Springer, 2002 |
| [21] | Kakutani T, Yamasaki N. Solitary waves on a two-layer fluid. J Phys Soc Jpn, 1978, 45(2): 674-679 |
| [22] | Hamdi S, Morse B, Halphen B, et al. Analytical solutions of long nonlinear internal waves: Part I. Nat Hazards, 2011, 57(3): 597-607 |
| [23] |
Grimshaw R, Pelinovsky D, Pelinovsky E, et al. Generation of large-amplitude solitons in the extended Korteweg-de Vries equation. Chaos, 2002, 12(4): 1070-1076
pmid: 12779630 |
| [24] | Fan E G. A family of completely integrable multi-Hamiltonian systems explicitly related to some celebrated equations. J Math Phys, 2001, 42(9): 4327-4344 |
| [25] | Meng G Q, Gao Y T, Yu X, et al. Painlevé analysis, Lax pair, Bäcklund transformation and multi-soliton solutions for a generalized variable-coefficient KdV-mKdV equation in fluids and plasmas. Phys Scr, 2012, 85(5): 055010 |
| [26] | Li J, Xu T, Meng X H, et al. Lax pair, Bäcklund transformation and N-soliton-like solution for a variable-coefficient Gardner equation from nonlinear lattice, plasma physics and ocean dynamics with symbolic computation. J Math Anal Appl, 2007, 336(2): 1443-1455 |
| [27] | El G A, Hoefer M A. Dispersive shock waves and modulation theory. Physica D, 2016, 333: 11-65 |
| [28] | Holloway P E, Pelinovsky E, Talipova T. A generalized Korteweg-de Vries model of internal tide transformation in the coastal zone. J Geophys Res Oceans, 1999, 104(C8): 18333-18350 |
| [29] | Scotti A, Pineda J. Observation of very large and steep internal waves of elevation near the Massachusetts coast. Geophys Res Lett, 2004, 31(22): L22307 |
| [30] | Madsen P A, Fuhrman D R, Schäffer H A. On the solitary wave paradigm for tsunamis. J Geophys Res Oceans, 2008, 113(C12): C12012 |
| [31] | Christie D R. The morning glory of the Gulf of Carpentaria: a paradigm for non-linear waves in the lower atmosphere. Austral Met Mag, 1992, 41: 21-60 |
| [32] | Smyth N F, Holloway P E. Hydraulic jump and undular bore formation on a shelf break. J Phys Ocean, 1988, 18(7): 947-962 |
| [33] | Whitham G B. Linear and Nonlinear Waves. New York: Wiley, 1974 |
| [34] | Whitham G B. Non-linear dispersive waves. Math Phys Sci, 1965, 283(1393): 238-261 |
| [35] | An X, Marchant T R, Smyth N F. Dispersive shock waves governed by the Whitham equation and their stability. Proc Math Phys Eng Sci, 2018, 474(2216): 20180278 |
| [36] | El G A, Hoefer M A, Shearer M. Dispersive and diffusive-dispersive shock waves for non-convex conservation laws. SIAM Review, 2017, 59(1): 3-61 |
| [37] | Onorato M, Stefania R, Fabio B. Rogue and Shock Waves in Nonlinear Dispersive Media. New York: Springer, 2016 |
| [38] | Gurevich A V, Pitaevskii L P. Nonstationary structure of a collisionless shock wave. Sov Phys JETP, 1974, 38: 291-297 |
| [39] | Kamchatnov A M. New approach to periodic solutions of integrable equations and nonlinear theory of modulational instability. Phys Rep, 1997, 286(4): 199-270 |
| [40] | Zhang Y, Hao H Q, Guo R. Periodic solutions and Whitham modulation equations for the Lakshmanan-Porsezian-Daniel equation. Phys Lett A, 2022, 450: 128369 |
| [41] | Zhang Y, Hao H Q. Whitham modulation theory and periodic solutions for the fifth-order nonlinear Schrödinger equation in the Heisenberg ferromagnetic spin chain. Nonlinear Dyn, 2023, 111: 12461-12477 |
| [42] | Wang D S, Xu L, Xuan Z. The complete classification of solutions to the Riemann problem of the defocusing complex modified KdV equation. J Nonlinear Sci, 2022, 32(1): 1-46 |
| [43] | Kamchatnov A M. Dispersive shock wave theory for nonintegrable equations. Phys Rev E, 2019, 99(1): 012203 |
| [44] | El G A, Gammal A, Khamis E G, et al. Theory of optical dispersive shock waves in photorefractive media. Phys Rev A, 2007, 76(5): 053813 |
| [45] | Driscoll C F, O' Neil T M. Modulational instability of cnoidal wave solutions of the modified Korteweg-de Vries equation. J Math Phys, 1975, 17(7): 1196-1200 |
| [46] | Kamchatnov A M, Spire A, Konotop V V. On dissipationless shock waves in a discrete nonlinear Schrödinger equation. J Phys A, 2004, 37(21): 5547 |
| [47] | Marchant T R. Undular bores and the initial-boundary value problem for the modified Korteweg-de Vries equation. Wave Motion, 2008, 45(4): 540-555 |
| [48] | Kodama Y, Pierce V U, Tian F R. On the Whitham equations for the defocusing complex modified KdV equation. SIAM J Math Anal, 2009, 40(5): 1750-1782 |
| [49] | Marchant T R, Smyth N F. The extended Korteweg-de Vries equation and the resonant flow of a fluid over topography. J Fluid Mech, 1990, 221: 263-287 |
| [50] | Kamchatnov A M, Kuo Y H, Lin T C, et al. Undular bore theory for the Gardner equation. Phys Rev E, 2012, 86(3): 036605 |
| [51] | Matveev B V. 30 years of finite-gap integration theory. Phil Trans R Soc A, 2008, 366(1867): 837-875 |
| [52] |
Kamchatnov A M, Kraenkel R A. On the relationship between a    |
| [53] | Ercolani N M, Jin S, Levermore C D, et al. The zero-dispersion limit for the odd flows in the focusing Zakharov-Shabat hierarchy. Int Math Res Notices, 2003, 47: 2529 |
| [54] | Grava T, Klein C. Numerical solution of the small dispersion limit of Korteweg-de Vries and Whitham equations. Commun Pure Appl Math, 2007, 60(11): 1623-1664 |
| [55] | Fornberg B, Whitham G B. A numerical and theoretical study of certain nonlinear wave phenomena. Philos Trans R Soc London Ser A, 1978, 289(1361): 373-404 |
| [1] | 王丽. 超音速流越过弯曲坡面的反问题[J]. 数学物理学报, 2018, 38(4): 679-686. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 318
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 70
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|