基于重对数律的非平稳性度量

摘要/Abstract

摘要：

时间序列的非平稳性与很多领域的应用密切相关. 如何衡量时间序列的非平稳程度是一个重要的研究课题, 已经构建了一个完整的非平稳性度量框架, 其中稳定集合的判别标准处于核心地位. 该文基于独立同分布随机变量的重对数律, 提出了一种新的稳定集合判别标准, 与已有标准相比, 在显著性水平相同的情况下, 收敛标准更为严格, 且所需的参数更少, 该方法提高了非平稳性度量在 NS 较小时的分辨率. 对于确定性信号的参数校准, 新方法得到的结果更为精确.

关键词: 非平稳性度量, 稳定集合, 重对数律

Abstract:

The non-stationarity of time series is closely related to its application in many fields. How to measure the non-stationarity of time series is an important research topic. A complete non-stationarity measurement framework has been constructed, in which the criterion of stable set is the core. In this paper, based on the law of iterated logarithm of independent identically distributed random variables, a new criterion of stable set is proposed. Compared with the existing criterion, the convergence criterion is more strict and requires fewer parameters when the level of significance is the same. This method improves the resolution of non-stationary measurement when NS is small. For the parameter calibration of deterministic signals, the new method can get more accurate results.

Key words: Non-stationary measure, Stable set, Law of the iterated logarithm

中图分类号:

O211

张聪, 丁义明. 基于重对数律的非平稳性度量[J]. 数学物理学报, 2023, 43(6): 1855-1868.

Zhang Cong, Ding Yiming. Non-stationarity Measurement Based on Law of Iterated Logarithm[J]. Acta mathematica scientia,Series A, 2023, 43(6): 1855-1868.

图/表 9

图1

图2

图3

图4

表1

图5

图6

图7

表2

参考文献 21

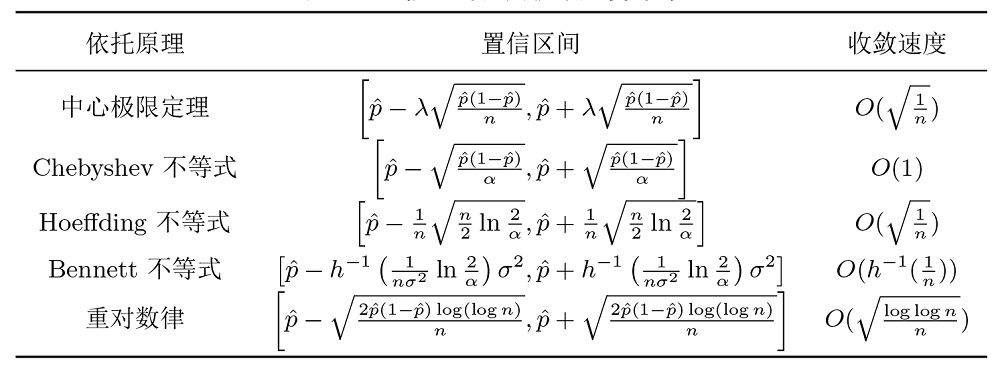
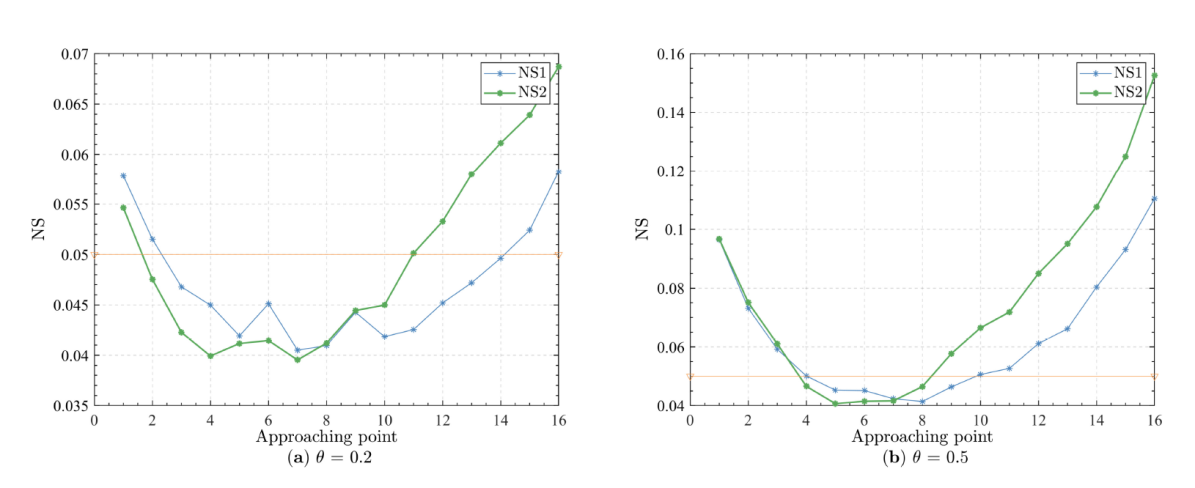
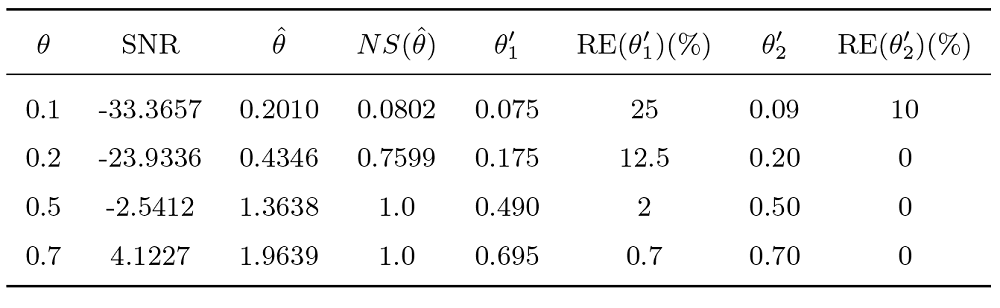
[1]	丁义明, 范文涛, 谭秋衡, 等. 数据流的非平稳性度量. 数学物理学报, 2010, 30A(5): 1364-1376
	Ding Y M, Fan W T, Tan Q H, et al. Nonstationarity measure of data stream. Acta Math Sci, 2010, 30A(5): 1364-1376
[2]	王晶. 非平稳时间序列的多尺度分析. 北京: 北京交通大学, 2015
	Wang J. Multiscale Analysis of Nonstationary Time Series. Beijing: Beijing Jiaotong University, 2015
[3]	刘罗曼. 时间序列平稳性检验. 沈阳师范大学学报(自然科学版), 2010, 28(3): 357-359
	Liu L M. Time series smoothness test. Journal of Shenyang Normal University (Natural Science Edition), 2010, 28(3): 357-359
[4]	谭秋衡. 时间序列的非平稳性度量及其应用. 武汉: 中国科学院研究生院(武汉物理与数学研究所), 2013
	Tan Q H. Non-stationary Measurement of Time Series and Its Application. Wuhan: Graduate School of Chinese Academy of Sciences (Wuhan Institute of Physics and Mathematics), 2013
[5]	吴量. 基于非平稳性度量的EMD趋势噪声分解. 武汉: 华中师范大学, 2013
	Wu L. EMD Trend Noise Decomposition Based on Non-smoothness Measure. Wuhan: Central China Normal University, 2013
[6]	兰军, 谭秋衡, 董前进. 基于非平稳度量的灌溉用水量预测模型选择. 武汉大学学报(工学版), 2014, 47(6): 721-725
	Lan J, Tan Q H, Dong Q J. Selection of forecasting models for irrigation water consumption based on nonstationarity measure. Engineering Journal of Wuhan University, 2014, 47(6): 721-725
[7]	吕洋. 基于非平稳性度量的数字印章信息匹配. 武汉: 武汉理工大学, 2020
	Lv Y. Information Matching of Digital Stamps Based on Non-smoothness Metric. Wuhan: Wuhan University of Technology, 2020
[8]	Tan Q H, Jiang H J, Ding Y M. Model selection method based on maximal information coefficient of residuals. Acta Mathematica Scientia, 2014, 34B(2): 579-592
[9]	Cover T M, Thomas J A. Elements of Information Theory. New York: Wiley-Interscience, 2006
[10]	谭秋衡, 丁义明. 基于非平稳性度量的彩票数据实证分析. 数学物理学报, 2014, 34A(1): 207-216
	Tan Q H, Ding Y M. Empirical analysis of lottery data based on non-stationarity measurement. Acta Math Sci, 2014, 34A(1): 207-216
[11]	谭秋衡, 吴量, 李波. 基于EMD及非平稳性度量的趋势噪声分解方法. 数学物理学报, 2016, 36A(4): 783-794
	Tan Q H, Wu L, Li B. Trend noise decomposition method based on EMD and non-stationarity measure. Acta Math Sci, 2016, 36A(4): 783-794
[12]	邹永杰. 用非平稳度量区分白噪声过程与鞅差分序列. 武汉: 武汉理工大学, 2011
	Zou Y J. Distinguishing White Noise Processes from Harnessed Difference Series Using a Non-smooth Metric. Wuhan: Wuhan University of Technology, 2011
[13]	张小彩. 概率中的一些不等式. 郑州: 郑州大学, 2010
	Zhang X C. Some Inequalities in Probability. Zhengzhou: Zhengzhou University, 2010
[14]	Yang X W, Song S, Zhang H M. Law of iterated logarithm and model selection consistency for generalized linear models with independent and dependent responses. Frontiers of Mathematics in China, 2021, 16: 825-856 doi: 10.1007/s11464-021-0900-2
[15]	Lorek P, Łoś G, Gotfryd K, Zagórski F. On testing pseudorandom generators via statistical tests based on the arcsine law. 2020, 380: 112968
[16]	Deo C M. A note on stationary Gaussian sequences. The Annals of Probability, 1974, 2(5): 954-957
[17]	Dzindzalieta D, Ileikis M, Jukeviius T. Optimal probability inequalities for random walks related to problems in extremal combinatorics. Siam Journal on Discrete Mathematics, 2011, 26(2): 828-837 doi: 10.1137/110834913
[18]	Teicher H. On the law of the iterated logarithm. The Annals of Probability, 1974, 2(4): 714-728
[19]	Zhou Z, Zhou Z, Wu L. Calibration for parameter estimation of signals with complex noise via nonstationarity measure. Complexity, 2021, 2021: Article ID 8840757
[20]	王志刚. 自回归模型的定阶方法选择及弱信号探测. 武汉: 武汉理工大学, 2020
	Wang Z G. Selection of Fixed-Order Methods for Autoregressive Models and Weak Signal Detection. Wuhan: Wuhan University of Technology, 2020
[21]	Alsmeyer G, Buckmann F. An arcsine law for Markov random walks. Stochastic Processes and Their Applications, 2019, 129(1): 223-239 doi: 10.1016/j.spa.2018.02.014