数学物理学报 ›› 2023, Vol. 43 ›› Issue (5): 1483-1518.
一类分数高斯噪声驱动的 Ornstein-Uhlenbeck 过程的参数估计: Hurst 参数 















- 1江西师范大学数学与统计学院 南昌 330022
2湘潭大学数学与计算科学学院 湖南湘潭 411105
-
收稿日期:2022-01-06修回日期:2023-04-10出版日期:2023-10-26发布日期:2023-08-09 -
通讯作者:李英 E-mail:liying@xtu.edu.cn -
基金资助:国家自然科学基金(11961033);国家自然科学基金(12171410);湖南省教育厅一般项目(22C0072)
Parameter Estimation for an Ornstein-Uhlenbeck Process Driven by a Type of Gaussian Noise with Hurst Parameter 















Chen Yong1,Li Ying2,*( ),Sheng Ying1,Gu Xiangmeng1
),Sheng Ying1,Gu Xiangmeng1
- 1School of Mathematics and Statistics, Jiangxi Normal University, Nanchang 330022
2School of Mathematics and Computional Science, Xiangtan University, Xiangtan 411105
-
Received:2022-01-06Revised:2023-04-10Online:2023-10-26Published:2023-08-09 -
Contact:Ying Li E-mail:liying@xtu.edu.cn -
Supported by:NSFC(11961033);NSFC(12171410);General Project of Hunan Provincial Education Department of China(22C0072)
摘要:
Chen 和 Zhou (2021) 研究了一类分数高斯过程 











































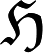































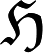
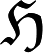

















中图分类号:
- O211.64
引用本文
陈勇,李英,盛英,古象盟. 一类分数高斯噪声驱动的 Ornstein-Uhlenbeck 过程的参数估计: Hurst 参数 







Chen Yong,Li Ying,Sheng Ying,Gu Xiangmeng. Parameter Estimation for an Ornstein-Uhlenbeck Process Driven by a Type of Gaussian Noise with Hurst Parameter 







使用本文
| [1] | Chen Y, Zhou H. Parameter estimation for an Ornstein-Uhlenbeck process driven by a general gaussian noise. Acta Mathematica Scientia, 2021, 41B(2): 573-595 |
| [2] | Alòs E, Mazet O, Nualart D. Stochastic calculus with respect to Gaussian processes. Ann Probab, 2001, 29(2): 766-801 |
| [3] | Hu Y Z, Jolis M, Tindel S. On Stratonovich and Skorohod stochastic calculus for Gaussian processes. Ann Probab, 2013, 41(3A): 1656-1693 |
| [4] | Douissi S, Es-Sebaiy K, Kerchev G, Nourdin I. Berry-Esseen bounds of second moment estimators for Gaussian processes observed at high frequency. Electronic Journal of Statistics, 2022, 16(1): 636-670 |
| [5] | Kutoyants Y A. Statistical Inference for Ergodic Diffusion Processes. New York: Springer, 2004 |
| [6] | Liptser R S, Shiryaev A N. Statistics of Random Processes II:Applications. New York: Springer, 2001 |
| [7] |
Kleptsyna M L, Le Breton A. Statistical analysis of the fractional Ornstein-Uhlenbeck type process. Stat Inference Stoch Process, 2002, 5: 229-248
doi: 10.1023/A:1021220818545 |
| [8] | Tudor C, Viens F. Statistical aspects of the fractional stochastic calculus. Ann Statist, 2007, 35(3): 1183-1212 |
| [9] |
Bercu B, Coutin L, Savy N. Sharp large deviations for the fractional Ornstein-Uhlenbeck process. Theory Probab Appl, 2011, 55(4): 575-610
doi: 10.1137/S0040585X97985108 |
| [10] |
Brouste A, Kleptsyna M. Asymptotic properties of MLE for partially observed fractional diffusion system. Stat Inference Stoch Process, 2010, 13(1): 1-13
doi: 10.1007/s11203-009-9035-x |
| [11] |
Hu Y, Nualart D. Parameter estimation for fractional Ornstein-Uhlenbeck processes. Stat Probab Lett, 2010, 80 (11/12): 1030-1038
doi: 10.1016/j.spl.2010.02.018 |
| [12] |
Hu Y, Nualart D, Zhou H. Parameter estimation for fractional Ornstein-Uhlenbeck processes of general Hurst parameter. Stat Inference Stoch Process, 2019, 22: 111-142
doi: 10.1007/s11203-017-9168-2 |
| [13] |
Sottinen T, Viitasaari L. Parameter estimation for the Langevin equation with stationary-increment Gaussian noise. Stat Inference Stoch Process, 2018, 21(3): 569-601
doi: 10.1007/s11203-017-9156-6 |
| [14] | Diedhiou A, Manga C, Mendy I. Parametric estimation for SDEs with additive sub-fractional Brownian motion. Journal of Numerical Mathematics and Stochastics, 2011, 3(1): 37-45 |
| [15] |
Cai C, Wang Q, Xiao W. Mixed sub-fractional Brownian motion and drift estimation of related Ornstein-Uhlenbeck process. Commun Math Stat, 2022, DOI: 10.1007/s40304-021-00245-8
doi: 10.1007/s40304-021-00245-8 |
| [16] | Basawa I V, Scott D J. Asymptotic Optimal Inference for Non-ergodic Models. New York: Springer, 1983 |
| [17] | Dietz H M, Kutoyants Y A. Parameter estimation for some non-recurrent solutions of SDE. Statistics and Decisions, 2003, 21(1): 29-46 |
| [18] | Belfadli R, Es-Sebaiy K, Ouknine Y. Parameter estimation for fractional Ornstein-Uhlenbeck processes: non-ergodic case. Front Sci Eng Int J Hassan II Acad Sci Technol, 2011, 1(1): 1-16 |
| [19] |
El Machkouri M, Es-Sebaiy K, Ouknine Y. Least squares estimator for non-ergodic Ornstein-Uhlenbeck processes driven by Gaussian processes. J Korean Stat Soc, 2016, 45: 329-341
doi: 10.1016/j.jkss.2015.12.001 |
| [20] |
Mendy I. Parametric estimation for sub-fractional Ornstein-Uhlenbeck process. Journal of Statistical Planning and Inference, 2013, 143 (4): 663-674
doi: 10.1016/j.jspi.2012.10.013 |
| [21] |
Alazemi F, Alsenafi A, Es-Sebaiy K. Parameter estimation for Gaussian mean-reverting Ornstein-Uhlenbeck processes of the second kind: non-ergodic case. Stoch Dyn, 2020, 20(2): 2050011
doi: 10.1142/S0219493720500112 |
| [22] |
Shevchenko R, Tudor C. A. Parameter estimation for the Rosenblatt Ornstein-Uhlenbeck process with periodic mean. Stat Inference Stoch Process, 2020, 23 (1): 227-247
doi: 10.1007/s11203-019-09200-5 |
| [23] | Shen G, Yu Q, Tang Z. The least squares estimator for an Ornstein-Uhlenbeck process driven by a Hermite process with a periodic mean. Acta Math Sci, 2021, 41B(2): 517-534 |
| [24] |
Chen Y, Li Y. Berry-Esseen bound for the parameter estimation of fractional Ornstein-Uhlenbeck processes with         doi: 10.1080/03610926.2019.1678641 |
| [25] |
Jolis M. On the Wiener integral with respect to the fractional Brownian motion on an interval. J Math Anal Appl, 2007, 330: 1115-1127
doi: 10.1016/j.jmaa.2006.07.100 |
| [26] |
Chen Y, Ding Z, Li Y. Berry-Esseen bounds and almost sure CLT for the quadratic variation of a class of Gaussian process. Communications in Statistics-Theory and Methods, 2023, DOI:10.1080/03610926.2023.2167055
doi: 10.1080/03610926.2023.2167055 |
| [27] | Pickands J. Asymptotic properties of the maximum in a stationary Gaussian process. Trans Am Math Soc, 1969, 145: 75-86 |
| [28] | Chen Y, Hu Y, Wang Z. Parameter estimation of complex fractional Ornstein-Uhlenbeck processes with fractional noise. ALEA Lat Am J Probab Math Stat, 2017, 14: 613-629 |
| [29] |
Shen G, Tang Z, Yin X. Least-squares estimation for the Vasicek model driven by the complex fractional Brownian motion. Stochastics, 2022, 94(4): 537-558
doi: 10.1080/17442508.2021.1959587 |
| [30] |
Chen Y, Li Y, Pei X. Parameter estimation for Vasicek model driven by a general Gaussian noise. Communications in Statistics-Theory and Methods, 2023, 52(9): 3132-3148
doi: 10.1080/03610926.2021.1967399 |
| [31] |
Es-Sebaiy K, Es.Sebaiy M. Estimating drift parameters in a non-ergodic Gaussian Vasicek-type model. Stat Methods Appl, 2021, 30(2): 409-436
doi: 10.1007/s10260-020-00528-4 |
| [32] | Kozachenko Y, Melnikov A, Mishura Y. On drift parameter estimation in models with fractional Brownian motion, Statistics: A Journal of Theoretical and Applied Statistics, 2015, 49(1): 35-62 |
| [33] | Hu Y. Analysis on Gaussian Spaces. Hackensack, NJ: World Scientific Publishing, 2017 |
| [34] | Stroock D W, Varadhan S R S. Multidimensional Diffusion Processes. Classics in Mathematics. Berlin: Springer-Verlag, 1979 |
| [35] | Nourdin I, Peccati G. Normal Approximations with Malliavin Calculus:from Stein's Method to Universality. Cambridge: Cambridge University Press, 2012 |
| [36] | Nualart D, Peccati G. Central limit theorems for sequences of multiple stochastic integrals. Ann Probab, 2005, 33(1): 177-193 |
| [37] | Houdré C, Pérez-Abreu V, Üstünel A S. Multiple Wiener-Itô integrals:an introductory survey//Houdre C, Perez-Abren V. Chaos Expansions, Multiple Wiener-Itô Integrals and Their Applications. Boca Raton: CRC Press, 1994 |
| [38] |
Kim Y T, Park H S. Optimal Berry-Esséen bound for statistical estimations and its application to SPDE. Journal of Multivariate Analysis, 2017, 155: 284-304
doi: 10.1016/j.jmva.2017.01.006 |
| [1] | 陈勇,古象盟. 分数Ornstein-Uhlenbeck 过程最小二乘估计改进的Berry-Esséen 界[J]. 数学物理学报, 2023, 43(3): 855-882. |
| [2] | 丁毅,郭精军. 时变混合分数布朗运动下带交易费用的亚式期权定价[J]. 数学物理学报, 2021, 41(4): 1135-1146. |
| [3] | 徐丽平,李治. 混合型随机微分方程的传输不等式[J]. 数学物理学报, 2021, 41(1): 227-236. |
| [4] | 吴量. 有限二阶矩情形与重尾情形下的Hurst参数[J]. 数学物理学报, 2020, 40(4): 1072-1082. |
| [5] | 桑利恒,陈振龙,郝晓珍. 双分数布朗运动重整化自相交局部时的光滑性[J]. 数学物理学报, 2020, 40(3): 796-810. |
| [6] | 杨朝强. 一类特殊混合跳扩散Black-Scholes模型的欧式回望期权定价[J]. 数学物理学报, 2019, 39(6): 1514-1531. |
| [7] | 崔静,梁秋菊,毕娜娜. 分数布朗运动驱动的带脉冲的中立性随机泛函微分方程的渐近稳定性[J]. 数学物理学报, 2019, 39(3): 570-581. |
| [8] | 张骅月, 陈万华, 曲立安. 分数Black-Scholes市场中的动态下跌风险[J]. 数学物理学报, 2011, 31(6): 1674-1682. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 511
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 120
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
