一类 2$\times$2 双曲偏微分系统的 PDP 边界控制

数学物理学报 ›› 2023, Vol. 43 ›› Issue (5): 1471-1482.

一类 2$\times$2 双曲偏微分系统的 PDP 边界控制

庞玉婷¹(),赵东霞^1,^*(),赵鑫²(),高彩霞¹()

¹中北大学数学学院太原 030051
²太原理工大学电气与动力工程学院太原 030024

收稿日期:2022-03-18 修回日期:2023-03-08 出版日期:2023-10-26 发布日期:2023-08-09
通讯作者: 赵东霞 E-mail:2116786325@qq.com;zhaodongxia6@sina.com;1808642517@qq.com;1519546532@qq.com
作者简介:庞玉婷，Email: 2116786325@qq.com;|赵鑫，Email: 1808642517@qq.com;|高彩霞，Email: 1519546532@qq.com
基金资助:
山西省基础研究计划资助项目(20210302123046)

The PDP Boundary Control for a Class of 2$\times$2 Hyperbolic Partial Differential System

Pang Yuting¹(),Zhao Dongxia^1,^*(),Zhao Xin²(),Gao Caixia¹()

¹School of Mathematics, North University of China, Taiyuan 030051
²School of Electrical and Power Engineering, Taiyuan University of Technology, Taiyuan 030024

Received:2022-03-18 Revised:2023-03-08 Online:2023-10-26 Published:2023-08-09
Contact: Dongxia Zhao E-mail:2116786325@qq.com;zhaodongxia6@sina.com;1808642517@qq.com;1519546532@qq.com
Supported by:
Fundamental Research Program of Shanxi Province(20210302123046)

摘要/Abstract

摘要：

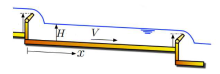
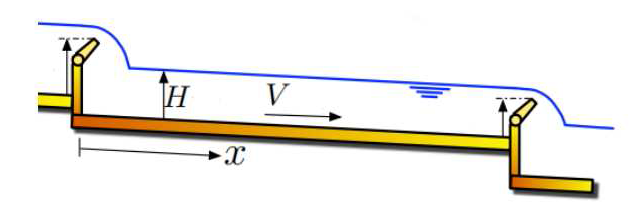
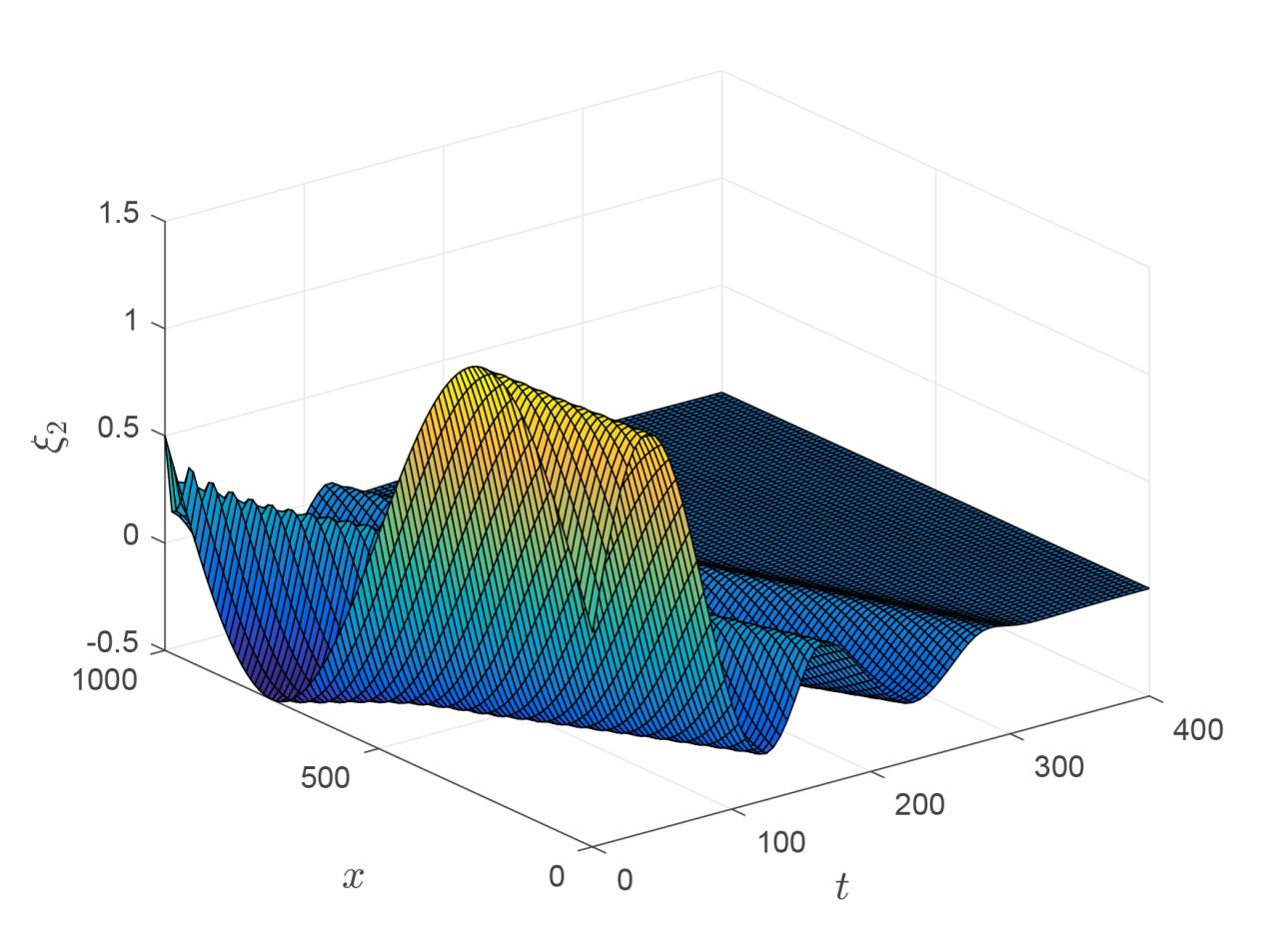
该文研究了具有恒定坡度和底部摩擦的单段明渠系统的指数稳定性, 该系统由$2\times2$双曲偏微分方程描述. 通过设计位置反馈和延迟位置反馈(简称PDP)边界控制器来解决系统的反馈镇定问题. 首先, 利用算子半群理论给出系统适定性的证明. 然后, 通过构造合适的Lyapunov函数分析闭环系统的指数稳定性, 并获得了反馈参数和时滞需要满足的充分条件. 此外, 还利用谱分析方法建立了系统算子特征根和特征向量的渐近表达式. 最后, 通过一个数值仿真示例来评估PDP控制器性能.

关键词: 双曲PDE系统, Lyapunov函数, PDP边界控制器, 指数稳定性

Abstract:

This paper studies the exponential stability of a single open-channel system with constant slope and bottom friction, which is described by a $2\times2$ hyperbolic partial differential equation. The position feedback and delayed position feedback (PDP for short) boundary controller is designed to solve the problem of feedback stabilization. Firstly, the well-posedness of the system is proved by using operator semigroup theory. Then, the exponential stability of the closed-loop system is analyzed by constructing an appropriate Lyapunov function, and sufficient conditions for feedback parameters and time-delay are obtained. In addition, the asymptotic expressions of the eigenvalues and the eigenfunctions of the system operator are given by spectral analysis method. Finally, a numerical example is used to evaluate the performance of the PDP controller.

Key words: Hyperbolic PDE system, Lyapunov function, PDP boundary controller, Exponential stability

中图分类号:

O231.4

庞玉婷,赵东霞,赵鑫,高彩霞. 一类 2$\times$2 双曲偏微分系统的 PDP 边界控制[J]. 数学物理学报, 2023, 43(5): 1471-1482.

Pang Yuting,Zhao Dongxia,Zhao Xin,Gao Caixia. The PDP Boundary Control for a Class of 2$\times$2 Hyperbolic Partial Differential System[J]. Acta mathematica scientia,Series A, 2023, 43(5): 1471-1482.

图/表 4

参考文献 31

[1]	Litrico X, Fromion V, Baume J P, et al. Experimental validation of a methodology to control irrigation canals based on Saint-Venant equations. Control Engineering Practice, 2005, 13(11): 1425-1437 doi: 10.1016/j.conengprac.2004.12.010
[2]	Santos V D, Prieur C. Boundary control of open channels with numerical and experimental validations. IEEE Transactions on Control Systems Technology, 2008, 16(6): 1252-1264 doi: 10.1109/TCST.2008.919418
[3]	Bastin G, Coron J M, Tamasoiu S O. Stability of linear density-flow hyperbolic systems under PI boundary control. Automatica, 2015, 53: 37-42 doi: 10.1016/j.automatica.2014.12.025
[4]	Zhang L G, Prieur C, Qiao J F. PI boundary control of linear hyperbolic balance laws with stabilization of ARZ traffic flow models. Systems & Control Letters, 2019, 123: 85-91 doi: 10.1016/j.sysconle.2018.11.005
[5]	Bastin G, Coron J M. Stability and Boundary Stabilization of 1-D Hyperbolic Systems. Switzerland: Birkhäuser, 2016
[6]	Vazquez R, Krstic M, Coron J M. Backstepping boundary stabilization and state estimation of a $2\times2$ linear hyperbolic system. Orlando: IEEE Conference on Decision and Control and European Control Conference, 2011
[7]	Litrico X, Fromion V. Boundary control of hyperbolic conservation laws using a frequency domain approach. Automatica, 2009, 45(3): 647-656 doi: 10.1016/j.automatica.2008.09.022
[8]	Bastin G, Coron J M, D'Andrea-Novel B, et al. Boundary control for exact cancellation of boundary disturbances in hyperbolic systems of conservation laws. Seville: IEEE Conference on Decision and Control, and the European Control Conference, 2005
[9]	Bastin G, Coron J M. Exponential stability of PI control for Saint-Venant equations with a friction term. Methods and Applications of Analysis, 2019, 26(2): 101-112 doi: 10.4310/MAA.2019.v26.n2.a1
[10]	Coron J M, D'Andrea-Novel B, Bastin G. A strict Lyapunov function for boundary control of hyperbolic systems of conservation laws. IEEE Transactions on Automatic Control, 2007, 52(1): 2-11 doi: 10.1109/TAC.2006.887903
[11]	Pazy A. Semigroup of Linear Operators and Applications to Partial Differential Equations. New York: Springer-Verlag, 1983
[12]	Hayat A, Shang P P. A quadratic Lyapunov function for Saint-Venant equations with arbitrary friction and space-varying slope. Automatica, 2019, 100: 52-60 doi: 10.1016/j.automatica.2018.10.035
[13]	Coron J M, Tamasoiu S O. Feedback stabilization for a scalar conservation law with PID boundary control. Chinese Annals of Mathematics, 2015, 36B(5): 763-776
[14]	Chentouf B, Wang J M. Boundary feedback stabilization and Riesz basis property of a 1-d first order hyperbolic linear system with $L^\infty$-coefficients. Journal of Differential Equations, 2009, 246(3): 1119-1138 doi: 10.1016/j.jde.2008.08.010
[15]	Trinh N T, Andrieu V, Xu C Z. Boundary PI controllers for a star-shaped network of $2\times2$ systems governed by hyperbolic partial differential equations. International Federation of Automatic Control, 2017, 50(1): 7070-7075
[16]	Trinh N T, Andrieu V, Xu C Z. Output regulation for a cascaded network of $2\times2$ hyperbolic systems with PI controller. Automatica, 2018, 91: 270-278 doi: 10.1016/j.automatica.2018.01.010
[17]	Aström K J, Hägglund T. PID Controllers: Theory, Design, and Tunning. Research Triangle Park, NC: ISA-The Instrumentation, Systems and Automation Society, 1995
[18]	Litrico X, Fromion V, Scorletti G. Robust feedforward boundary control of hyperbolic conservation laws. Networks and Heterogeneous Media, 2017, 2(4): 717-731 doi: 10.3934/nhm.2007.2.717
[19]	Bastin G, Coron J M, Hayat A. Feedforward boundary control of $2\times2$ nonlinear hyperbolic systems with application to Saint-Venant equations. European Journal of Control, 2021, 57: 41-53 doi: 10.1016/j.ejcon.2020.11.002
[20]	Tallman G, Smith O. Analog study of dead-beat posicast control. Ire Transactions on Automatic Control, 2003, 4(1): 14-21 doi: 10.1109/TAC.1958.1104844
[21]	Silva G J, Datta A, Bhattacharyya S P. PID Controllers for Time-Delay Systems. Boston: Birkhäuser, 2005
[22]	Cai G, Chen L. Some problems of delayed feedback control. Advances in Mechanics, 2013, 43(1): 21-28
[23]	Suh I H, Bien Z. Proportional minus delay controller. IEEE Transactions on Automatic Control, 1979, 24(2): 370-372 doi: 10.1109/TAC.1979.1102024
[24]	Suh I H, Bien Z. Use of time-delay actions in the controller design. IEEE Transactions on Automatic Control, 1980, 25: 600-603 doi: 10.1109/TAC.1980.1102347
[25]	Atay F M. Balancing the inverted pendulum using position feedback. Applied Mathematics Letters, 1999, 12(5): 51-56
[26]	Hu H Y. Using delayed state feedback to stabilize periodic motions of an oscillator. Journal of Sound and Vibration, 2004, 275(3-5): 1009-1025 doi: 10.1016/j.jsv.2003.07.006
[27]	Liu B, Hu H. Stabilization of linear undamped systems via position and delayed position feedbacks. Journal of Sound and Vibration, 2008, 312(3): 509-525 doi: 10.1016/j.jsv.2007.11.001
[28]	Krstic M. Control of an unstable reaction-diffusion PDE with long input delay. Systems & Control Letters, 2009, 58(10/11): 773-782 doi: 10.1016/j.sysconle.2009.08.006
[29]	范东霞, 赵东霞, 史娜, 等. 一类扩散波方程的PDP反馈控制和稳定性分析. 数学物理学报, 2021, 41A(4): 1088-1096
	Fan D X, Zhao D X, Shi N, et al. The PDP feedback control and stability analysis of a diffusive wave equation. Acta Mathematica Scientia, 2021, 41A(4): 1088-1096
[30]	Bastin G, Coron J M, D'Andrea-Novel B. On Lyapunov stability of linearised Saint-Venant equations for a sloping channel. Networks and Heterogeneous Media, 2009, 4(2): 177-187 doi: 10.3934/nhm.2009.4.177
[31]	Zhao D X, Fan D X, Guo Y P. The spectral analysis and exponential stability of a 1-d $2\times2$ hyperbolic system with proportional feedback control. International Journal of Control, Automation and Systems, 2022, 20(8): 2633-2640 doi: 10.1007/s12555-021-0507-0