数学物理学报 ›› 2023, Vol. 43 ›› Issue (3): 883-895.
一类椭圆型界面问题的数值算法
- 哈尔滨师范大学数学科学学院 哈尔滨 150025
-
收稿日期:2022-11-16修回日期:2023-01-12出版日期:2023-06-26发布日期:2023-06-01 -
通讯作者:牛晶 E-mail:qq63192678@126.com -
基金资助:国家青年自然科学基金项目(12101164);哈尔滨师范大学硕士研究生创新科研项目(HSDSSCX2022-40)
A Kind of Numerical Algorithm for Elliptic Interface Problem
- School of Mathematics and Sciences, Harbin Normal University, Harbin 150025
-
Received:2022-11-16Revised:2023-01-12Online:2023-06-26Published:2023-06-01 -
Contact:Jing Niu E-mail:qq63192678@126.com -
Supported by:Youth Fund of NSFC(12101164);Postgraduate Innovative Scientific Research Project of Harbin Normal University(HSDSSCX2022-40)
摘要:
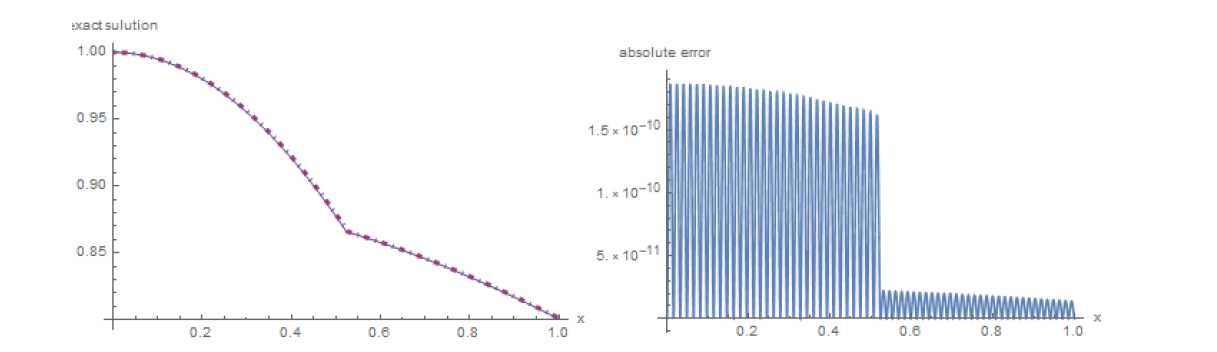
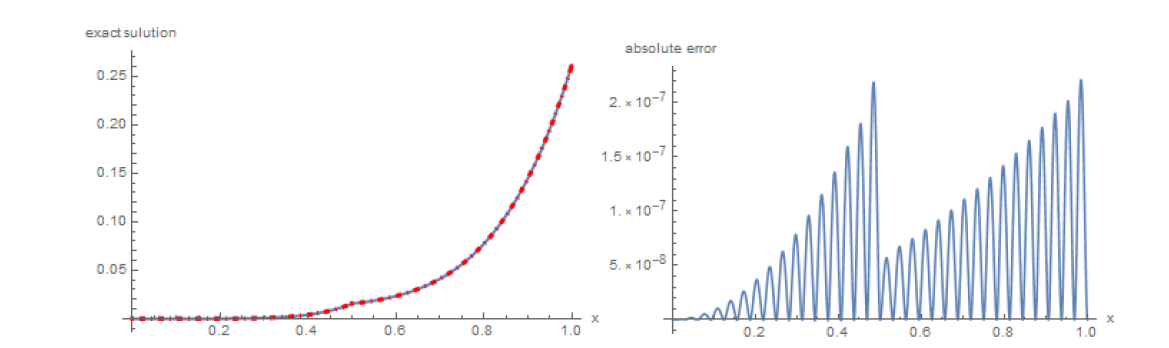
该文基于再生核空间相关理论提出了一种一维椭圆界面问题的数值算法. 该方法通过积分
中图分类号:
- O241.8
引用本文
于一康,牛晶. 一类椭圆型界面问题的数值算法[J]. 数学物理学报, 2023, 43(3): 883-895.
Yu Yikang,Niu Jing. A Kind of Numerical Algorithm for Elliptic Interface Problem[J]. Acta mathematica scientia,Series A, 2023, 43(3): 883-895.
使用本文
| [1] |
Greengard L, Moura M. On the numerical evaluation of electrostatic fields in composite materials. Acta Numer, 1994, 3: 379-410
doi: 10.1017/S0962492900002464 |
| [2] | Peskin C. Numerical analysis of blood flow in the heart. J Comput Phys, 1977, 25: 220-252 |
| [3] |
Al-Smadi M, Arqub O A. Computational algorithm for solving Fredholm time-fractional partial integrodifferential equations of Dirichlet functions type with error estimates. Appl Math Comput, 2019, 342: 280-294
doi: 10.1016/j.amc.2018.09.020 |
| [4] |
Al-Smadi M, Arqub O A, Shawagfeh N, Momani S. Numerical investigations for systems of second-order periodic boundary value problems using reproducing kernel method. Appl Math Comput, 2016, 291: 137-148
doi: 10.1016/j.amc.2016.06.002 |
| [5] |
Albright J, Epshteyn Y, Medvinsky M, Xia Q. High-order numerical schemes based on difference potentials for 2D elliptic problems with material interfaces. Appl Numer Math, 2017, 111: 64-91
doi: 10.1016/j.apnum.2016.08.017 |
| [6] |
Babuska I, Caloz G, Osborn J. Special finite element methods for a class of second order elliptic problems with rough coefficients. SIAM J Numer Anal, 1994, 31: 945-981
doi: 10.1137/0731051 |
| [7] |
Epshteyn Y, Phippen S. High-order difference potentials methods for 1D elliptic type models. Appl Numer Math, 2015, 93: 69-86
doi: 10.1016/j.apnum.2014.02.005 |
| [8] |
Hellrung J, Wang L, Sifakis E, Teran J. A second order virtual node method for elliptic problems with interfaces and irregular domains in three dimensions. J Comput Phys, 2012, 231: 2015-2048
doi: 10.1016/j.jcp.2011.11.023 |
| [9] |
Lee C, Park J. Preconditioning for finite element methods with strain smoothing. Computers & Mathematics with Applications, 2023, 130: 41-57
doi: 10.1016/j.camwa.2022.11.018 |
| [10] |
Kalachikova U, Vasilyeva M, Harris I, et al. Generalized Multiscale Finite Element Method for scattering problem in heterogeneous media. J Comput Appl Math, 2023, 424: 114977
doi: 10.1016/j.cam.2022.114977 |
| [11] |
Guzman J, Sanchez M, Sarkis M. On the accuracy of finite element approximations to a class of interface problems. Math Comput, 2016, 85: 2071-2098
doi: 10.1090/mcom/2016-85-301 |
| [12] | Harari I, Dolbow J. Analysis of an efficient finite element method for embedded interface problems. Comput Math, 2010, 46: 205-211 |
| [13] |
Dong B Y, Feng X F, Lin Z L. An FE-FD method for anisotropic elliptic interface problems. SIAM J Sci Comput, 2020, 42: B1041-B1066
doi: 10.1137/19M1291030 |
| [14] |
Pan K J, Wu X X, Xu Y F, Yuan G W. An exact-interface-fitted mesh generator and linearity-preserving finite volume scheme for anisotropic elliptic interface problems. J Comput Phys, 2022, 463: 111293
doi: 10.1016/j.jcp.2022.111293 |
| [15] |
Cao W, Zhang X, Zhang Z. Superconvergence of immersed finite element methods for interface problems. Adv Comput Math, 2017, 43: 795-821
doi: 10.1007/s10444-016-9507-7 |
| [16] | He X, Lin T, Lin Y. Immersed finite element methods for elliptic interface problems with non-homogeneous jump conditions. Int J Numer Anal Model, 2011, 8: 284-301 |
| [17] |
Cao W, Zhang X, Zhang Z, Zou Q. Superconvergence of immersed finite volume methods for one-dimensional interface problems. J Sci Comput, 2017, 73: 543-565
doi: 10.1007/s10915-017-0532-6 |
| [18] | Liu K, Zou Q. Analysis of a special immersed finite volume method for elliptic interface problems. Int J Numer Anal Model, 2019, 16: 964-984 |
| [19] |
Liu W, Jun S, Zhang Y. Reproducing kernel particle method. Int J Numer Methods Fluids, 1995, 20: 1081-1106
doi: 10.1002/(ISSN)1097-0363 |
| [20] |
Yang J, Guan P, Fan C. Weighted reproducing kernel collocation method and error analysis for inverse Cauchy problems. Int J Appl Mech, 2016, 8: 1650030
doi: 10.1142/S1758825116500307 |
| [21] |
Yang J, Hsin W. Weighted reproducing kernel collocation method based on error analysis for solving inverse elasticity problems. Acta Mech, 2019, 230: 3477-3497
doi: 10.1007/s00707-019-02473-0 |
| [22] | Chen J, Wang H, Hu H. Reproducing kernel enhanced local radial basis collocation method. Int J Numer Methods Eng, 2008, 80: 600-627 |
| [23] |
Niu J, Xu M, Yao G M. An efficient reproducing kernel method for solving the allen-cahn equation. Appl Math Lett, 2019, 89: 78-84
doi: 10.1016/j.aml.2018.09.013 |
| [24] |
Niu J, Sun L X, Xu M Q, Hou J J. A reproducing kernel method for solving heat conduction equations with delay. Appl Math Lett, 2020, 100: 106036
doi: 10.1016/j.aml.2019.106036 |
| [25] |
Niu J, Jia Y T, Sun J D. A new piecewise reproducing kernel function algorithm for solving nonlinear hamiltonian systems. Appl Math Lett, 2023, 136: 108451
doi: 10.1016/j.aml.2022.108451 |
| [26] |
Sun L X, Niu J, Hou J J. A high order convergence collocation method based on the reproducing kernel for general interface problems. Appl Math Lett, 2021, 112: 106718
doi: 10.1016/j.aml.2020.106718 |
| [27] |
Yu Y, Niu J, Zhang J, Ning S Y. A reproducing kernel method for nonlinear C-q-fractional IVPs. Appl Math Lett, 2022, 125: 107751
doi: 10.1016/j.aml.2021.107751 |
| [28] | Yu Y K, Niu J, Yang X M, Cui M G. A broken reproducing kernel method for the multiple interface problems, Comput Appl Math, 2022, 41: 260 |
| [29] | 吴勃英, 林迎珍. 应用型再生核空间. 北京: 科学出版社, 2012 |
| Wu B, Lin Y Z. Applied Regenerative Nuclear Space. Beijing: Science Press, 2012 | |
| [30] |
杨学敏, 牛晶, 姚春华. 椭圆型界面问题的破裂再生核方法. 计算数学, 2022, 44(2): 217-232
doi: 10.12286/jssx.j2021-0791 |
|
Yang X M, Niu J, Yao C H. The method of fracture regeneration core for elliptical interface problem. Computational Mathematics, 2022, 44(2): 217-232
doi: 10.12286/jssx.j2021-0791 |
|
| [31] |
Hall C A, Meyer W W. Optimal error bounds for cubic spline interpolation. J Approx Theory, 1976, 16: 105-122
doi: 10.1016/0021-9045(76)90040-X |
| [32] |
Xu M, Zhao Z, Niu J, Lin Y. A simplified reproducing kernel method for 1-D elliptic type interface problems. J Comput Appl Math, 2019, 351: 29-40
doi: 10.1016/j.cam.2018.10.027 |
| [33] | 林群, 谢和虎. 有限元Aubin-Nitsche技巧新认识及其应用. 数学的实践与认识, 2011, 41(17): 247-258 |
| Lin Q, Xie H. An observation on Aubin-Nitsche lemma and its applications. Mathematics in Practice and Theory, 2011, 41(17): 247-258 |
| [1] | 葛志昊,李瑞华. Bogoliubov-Tolmachev-Shirkov模型临界温度和能隙解的数值方法[J]. 数学物理学报, 2020, 40(6): 1699-1711. |
| [2] | 张晶,余旌胡. 线性回归模型参数估计方法的分辨率[J]. 数学物理学报, 2020, 40(5): 1381-1392. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 304
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 109
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|