数学物理学报 ›› 2023, Vol. 43 ›› Issue (2): 604-624.
考虑病毒DNA核衣壳和细胞间传播的一般HBV扩散模型
- 1山西大学复杂系统研究所 太原 030006
2黔南民族师范学院数学与统计学院 贵州都匀 558000
-
收稿日期:2022-01-29修回日期:2022-10-17出版日期:2023-04-26发布日期:2023-04-17 -
通讯作者:李雅芝,E-mail:lyz900101@126.com -
基金资助:国家自然科学基金项目(12126349);国家自然科学基金项目(11901326);贵州省科学技术基金(黔科合基础-ZK[2021]一般002);山西省卫健委资助项目(2020XM18)
A Generalized HBV Diffusive Model with DNA-Containing Capsids and Cell-Cell Infection
Liu Lili1,Wang Honggang1,Li Yazhi2,*( )
)
- 1Complex System Research Center, Shanxi University, Taiyuan 030006
2School of Mathematics and Statistics, Qiannan Normal University for Nationalities, Guizhou Duyun 558000
-
Received:2022-01-29Revised:2022-10-17Online:2023-04-26Published:2023-04-17 -
Supported by:NSFC(12126349);NSFC(11901326);Science and Technology Foundation of Guizhou Province, China(Qian Ke He Jichu-ZK[2021]002);National Health Commission Foundation of Shanxi Province(2020XM18)
摘要:
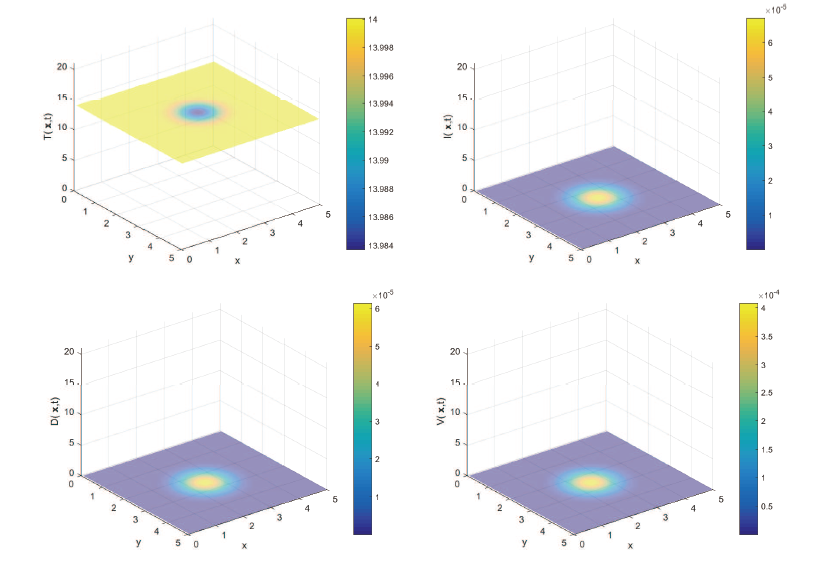
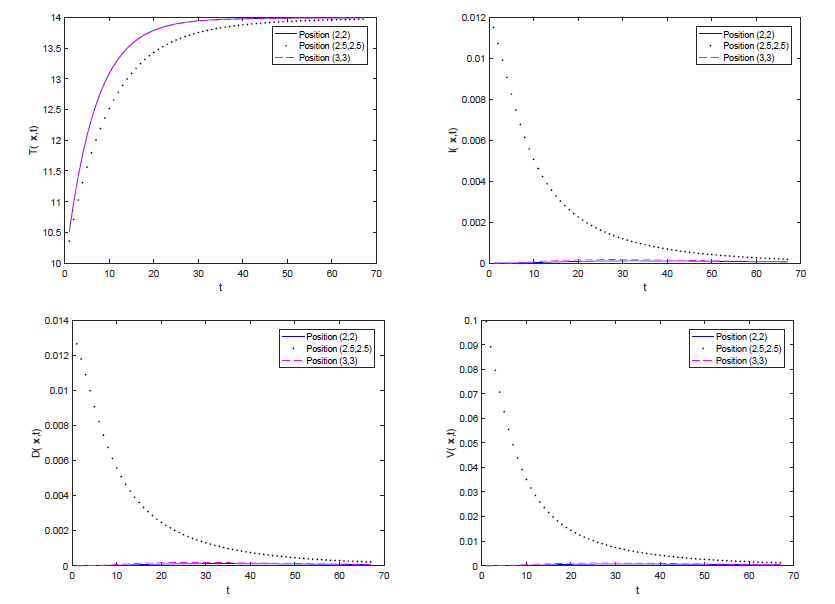
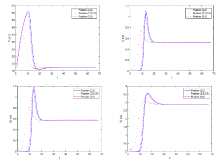
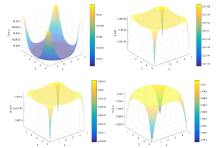
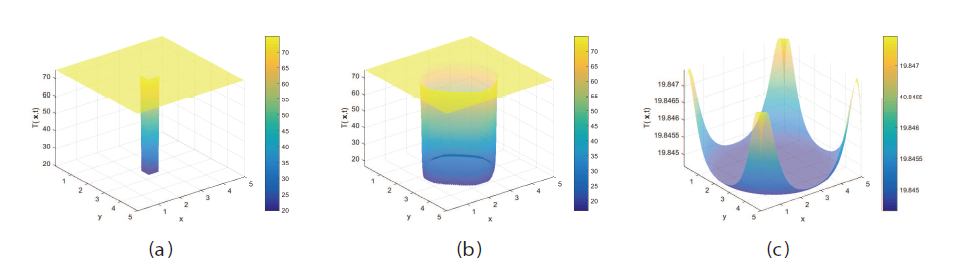
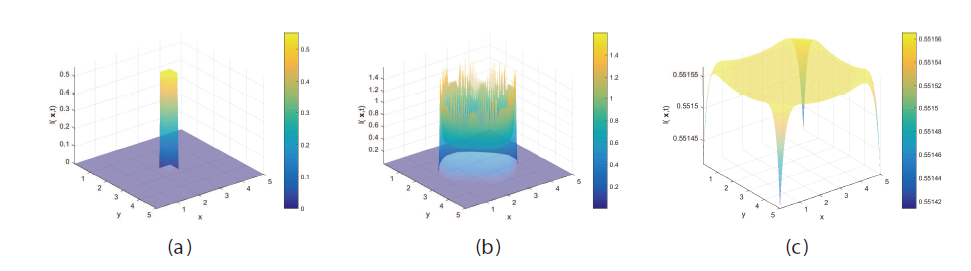
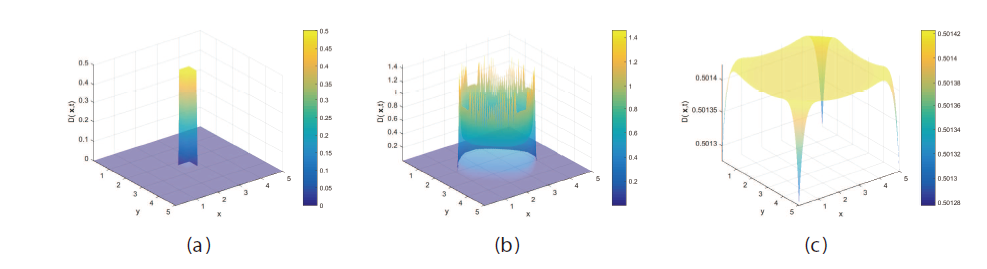
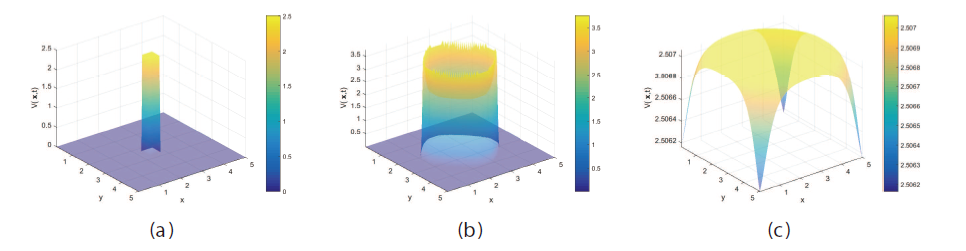
该文综合考虑了诱发HBV感染的两类途径、一般发生率函数和HBV病毒及其核衣壳的扩散效应, 建立了一般性的HBV 扩散模型. 证明了模型解的适定性, 两类平衡态的存在唯一性和模型的一致持久性, 然后通过构造Lyapunov 函数, 得出模型的阈值动力学行为. 最后结合数值模拟验证理论结果的同时, 揭示了扩散对各状态变量的影响, 结果显示: 扩散影响HBV感染, 且扩散系数越大, HBV感染的空间区域越大.
中图分类号:
- O175
引用本文
刘利利, 王洪刚, 李雅芝. 考虑病毒DNA核衣壳和细胞间传播的一般HBV扩散模型[J]. 数学物理学报, 2023, 43(2): 604-624.
Liu Lili, Wang Honggang, Li Yazhi. A Generalized HBV Diffusive Model with DNA-Containing Capsids and Cell-Cell Infection[J]. Acta mathematica scientia,Series A, 2023, 43(2): 604-624.
使用本文
| [1] |
Li M L, Zu J. The review of differential matrix models of HBV infection dynamics. J Virol Methods, 2019, 266: 103-113
doi: 10.1016/j.jviromet.2019.01.014 |
| [2] |
Nowak M A, Bonhoeffer S, Hill A M, et al. Viral dynamics in Hepatitis B virus infection. P Natl Acad Sci USA, 1996, 93(9): 4398-4402
doi: 10.1073/pnas.93.9.4398 |
| [3] | Min L, Su Y M, Kuang Y. Mathematical analysis of a basic virus infection model with application to HBV infection. Rocky Mountain J Math, 2008, 38(5): 1573-1585 |
| [4] | 李喜玲, 高飞, 李文琴. 具有免疫时滞的分数阶 HBV 感染模型稳定性分析. 数学物理学报, 2021, 41A(2): 562-576 |
| Li X L, Gao F, Li W Q. Stability analysis of fractional-order hepatitis B virus infection model with immune delay. Acta Math Sci, 2021, 41A(2): 562-576 | |
| [5] |
Wang K F, Wang W D. Propagation of HBV with spatial dependence. Math Biosci, 2007, 210(1): 78-95
pmid: 17592736 |
| [6] |
Wang K F, Wang W D, Song S P. Dynamics of an HBV model with diffusion and delay. J Theor Biol, 2008, 253(1): 36-44
pmid: 18155252 |
| [7] |
Gan Q T, Xu R, Yang P H, et al. Travelling waves of a hepatitis B virus infection model with spatial diffusion and time delay. IMA J Appl Math, 2010, 75(3): 392-417
doi: 10.1093/imamat/hxq009 |
| [8] |
Xu R, Ma Z N. An HBV model with diffusion and time delay. J Theor Biol, 2009, 257(3): 499-509
doi: 10.1016/j.jtbi.2009.01.001 pmid: 19174169 |
| [9] |
Zhang Y Y, Xu Z T. Dynamics of a diffusive HBV model with delayed Beddington-Deangelis response. Nonlinear Anal RWA, 2014, 15: 118-139
doi: 10.1016/j.nonrwa.2013.06.005 |
| [10] | 杨瑜, 周金玲. 一类具有扩散和Beddington-DeAngelis反应函数的病毒模型的全局稳定性. 高校应用数学学报, 2016, 31(2): 161-166 |
| Yang Y, Zhou J L. Global stability of a diffusive virus dynamics model with Beddington-DeAngelis incidence function. Appl Math Journal of Chinese Universities, 2016, 31(2): 161-166 | |
| [11] | Hattaf K, Yousfi N. A generalized HBV model with diffusion and two delays. Comput Math Appl, 2015, 69(1): 31-40 |
| [12] |
Guidotti L G, Rochford R, Chung J, et al. Viral clearance without destruction of infected cells during acute HBV infection. Science, 1999, 284: 825-829
doi: 10.1126/science.284.5415.825 pmid: 10221919 |
| [13] | Goyal A, Murray J M. Modelling the impact of cell-to-cell transmission in hepatitis B virus. Plos ONE, 2016, 11( 8): e0161978 |
| [14] | 杨翠兰, 刘贤宁. 一个具有细胞-细胞传播和时滞的病毒动力学模型. 西南大学学报(自然科学版), 2015, 37(5): 97-101 |
| Yang C L, Liu X N. A virus dynamical model with cell-to-cell viral transmission and delay. Journal of Southwest University of China (Natural Science Edition), 2015, 37(5): 97-101 | |
| [15] | Sun H Q, Wang J L. Dynamics of a diffusive virus model with general incidence function, cell-to-cell transmission and time delay. Comput Math Appl, 2019, 77(1): 284-301 |
| [16] |
Manna K, Chakrabarty S. P. Chronic Hepatitis B infection and HBV DNA-containing capsids: modeling and analysis. Commun Nonlinear Sci Numer Simulat, 2015, 22(1-3): 383-395
doi: 10.1016/j.cnsns.2014.08.036 |
| [17] |
Liu S H, Zhang R. On an age-structured Hepatitis B virus infection model with HBV DNA-containing capsids. Bull Malays Math Sci Soc, 2021, 44(3): 1345-1370
doi: 10.1007/s40840-020-01014-6 |
| [18] | Manna K. Dynamics of a diffusion-driven HBV infection model with capsids and time delay. Int J Biomath, 2017, 10( 5): 1750062 |
| [19] | Guo T, Liu H H, Xu C L, et al. Global stability of a diffusive and delayed HBV infection model with HBV DNA-containing capsids and general incidence rate. Discret Contin Dyn Syst Ser B, 2018, 23(10): 4223-4242 |
| [20] |
Manna K, Hattaf H. Spatiotemporal dynamics of a generalized HBV infection model with capsids and adaptive immunity. Int J Appl Comput Math, 2019, 5: 65
doi: 10.1007/s40819-019-0651-x |
| [21] |
Webb G F. A reaction-diffusion model for a deterministic diffusive epidemic. J Math Anal Appl, 1981, 84(1): 150-161
doi: 10.1016/0022-247X(81)90156-6 |
| [22] | Webb G F. Theory of Nonlinear Age-Dependent Population Dynamics. New York: Marcell Dekker Inc, 1985 |
| [23] | Protter M H, Weinberger H F. Maximum Principles in Differential Equations. New York: Springer Science & Business Media, 2012 |
| [24] |
Wang J L, Wang J. Analysis of a reaction-diffusion cholera model with distinct dispersal rates in the human population. J Dyn Differ Equ, 2021, 33: 549-575
doi: 10.1007/s10884-019-09820-8 |
| [25] | Hale J K. Asymptotic Behavior of Dissipative Systems. Providence: Amer Math Soc, 1988 |
| [26] | Hale J K, Lunel S M V. Introduction to Functional Differential Equations. Vol 99. New York:Springer Science & Business Media, 2013 |
| [27] |
Smith H L, Zhao X Q. Robust persistence for semidynamical systems. Nonlinear Anal: TMA, 2001, 47(9): 6169-6179
doi: 10.1016/S0362-546X(01)00678-2 |
| [1] | 李江,蓝桂杰,张树文,魏春金. 一类随机葡萄糖-胰岛素模型动力学分析[J]. 数学物理学报, 2021, 41(6): 1937-1949. |
| [2] | 丰利香,王德芬. 具有隔离和不完全治疗的传染病模型的全局稳定性[J]. 数学物理学报, 2021, 41(4): 1235-1248. |
| [3] | 周永辉. 一类具有时滞的非局部反应扩散方程非单调临界行波解的全局稳定性[J]. 数学物理学报, 2020, 40(4): 983-992. |
| [4] | 靖晓洁, 赵爱民, 刘桂荣. 考虑部分免疫和环境传播的麻疹传染病模型的全局稳定性[J]. 数学物理学报, 2019, 39(4): 909-917. |
| [5] | 韦爱举, 张新建, 王俊义, 李科赞. 一类埃博拉传染病模型的动力学分析[J]. 数学物理学报, 2017, 37(3): 577-592. |
| [6] | 黄祖达. 一类具反馈控制的时滞飞蝇方程的伪概周期解[J]. 数学物理学报, 2016, 36(3): 558-568. |
| [7] | 李玉环, 周军, 穆春来. 对带有非局部时滞和扩散的捕食者-食饵系统的稳定性分析[J]. 数学物理学报, 2012, 32(3): 475-488. |
| [8] | 崔诚, 王晓, 高飞, 刘安平. 多元产品价格互惠时滞模型的周期解和概周期解及其全局稳定性[J]. 数学物理学报, 2011, 31(6): 1718-1729. |
| [9] | 吴事良;李万同. 具有阶段结构的Lotka-Volterra合作系统的稳定性和行波解[J]. 数学物理学报, 2008, 28(3): 454-464. |
| [10] | 桂占吉; 贾敬; 葛渭高. 具有时滞的单种群扩散模型的全局稳定性[J]. 数学物理学报, 2007, 27(3): 496-505. |
| [11] | 梁志清;陈兰荪. 离散Leslie捕食与被捕食系统周期解的稳定性[J]. 数学物理学报, 2006, 26(4): 634-640. |
| [12] | 曾志刚, 廖晓昕. 无界变时滞神经网络全局稳定性[J]. 数学物理学报, 2005, 25(5): 621-626. |
| [13] | 原三领, 马知恩, 韩茂安. 一类含时滞SIS流行病模型的全局稳定性[J]. 数学物理学报, 2005, 25(3): 349-356. |
| [14] | 宋新宇, 肖燕妮, 陈兰荪. 具有时滞的生态流行病模型的稳定性和Hopf分支[J]. 数学物理学报, 2005, 25(1): 57-66. |
| [15] | 杨昌利, 阮荣耀, 龚妙昆. 一类不确定性非线性系统的状态反馈鲁棒自适应控制器的设计与分析[J]. 数学物理学报, 2004, 24(1): 26-37. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 292
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 68
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|