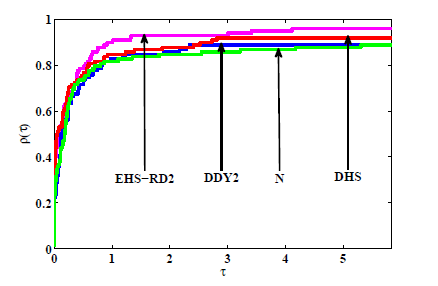
数学物理学报 ›› 2023, Vol. 43 ›› Issue (2): 570-580.
两个带重启方向的改进 HS 型共轭梯度法
- 中国矿业大学数学学院 江苏徐州 221116
-
收稿日期:2022-02-11修回日期:2022-10-17出版日期:2023-04-26发布日期:2023-04-17 -
通讯作者:吴彦强,E-mail: wyq1976819@126.com -
作者简介:刘鹏杰,E-mail:liupengjie2019@163.com -
基金资助:国家自然科学基金(72071202);中央高校基本科研业务费专项资金(2017XKQY090);江苏省研究生科研与实践创新计划(KYCX22_2491);中国矿业大学研究生创新计划(2022WLKXJ021);和中国矿业大学数学研究项目(2022DLZD04-203)
Two Extended HS-type Conjugate Gradient Methods with Restart Directions
Liu Pengjie( ),Wu Yanqiang(
),Wu Yanqiang( ),Shao Feng,Zhang Yan,Shao Hu
),Shao Feng,Zhang Yan,Shao Hu
- School of Mathematics, China University of Mining and Technology, Jiangsu Xuzhou 221116
-
Received:2022-02-11Revised:2022-10-17Online:2023-04-26Published:2023-04-17 -
Supported by:National Natural Science Foundation of China(72071202);Fundamental Research Funds for the Central Universities(2017XKQY090);Postgraduate Research & Practice Innovation Program of Jiangsu Province(KYCX22_2491);Graduate Innovation Program of China University of Mining and Technology(2022WLKXJ021);Teaching and Research Project of CUMT(2022DLZD04-203)
摘要:
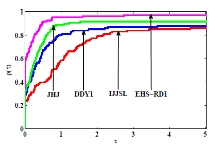
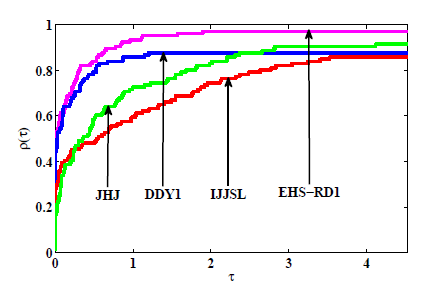
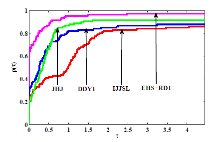
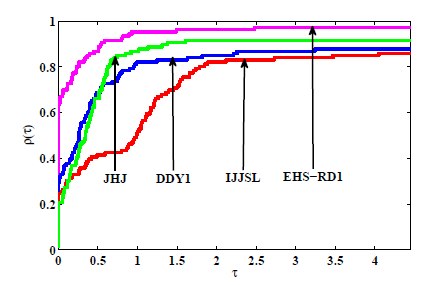
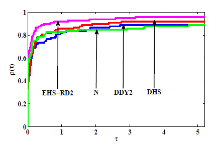
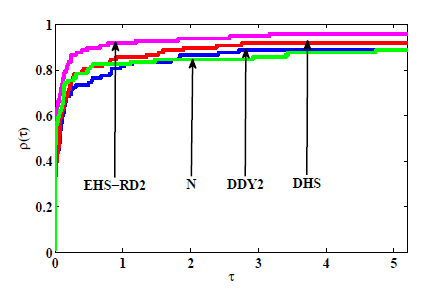
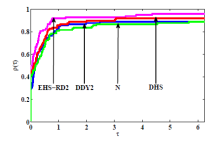
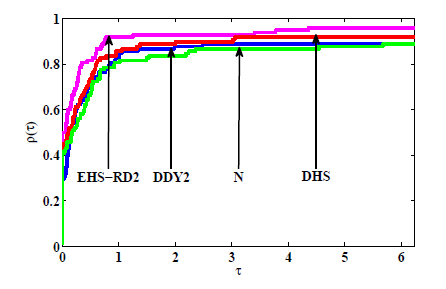
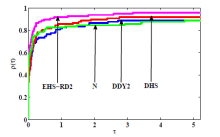
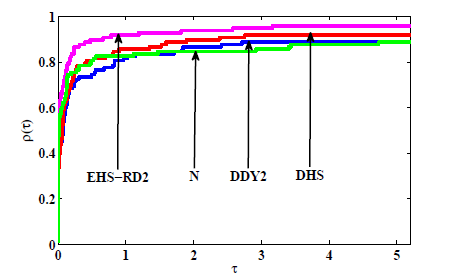
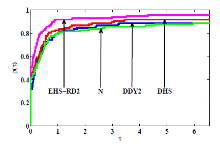
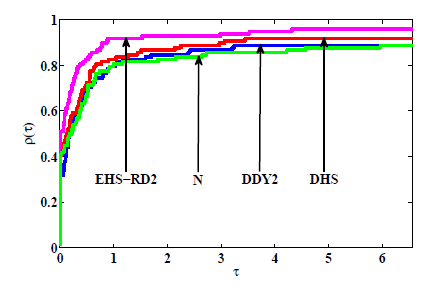
共轭梯度法是求解大规模无约束优化的有效方法之一. 该文首先对 Hestenes-Stiefel (HS) 共轭参数改进,再通过引入重启条件及重启方向, 建立两个带重启方向的改进 HS 型共轭梯度法. 第一个方法在弱 Wolfe 线搜索下产生下降方向, 第二个方法独立于任何线搜索得到充分下降性. 常规假设下, 分析并获得两个新方法的全局收敛性. 最后, 数值比对试验结果及性能图显示新方法是有效的.
中图分类号:
- O221.2
引用本文
刘鹏杰, 吴彦强, 邵枫, 张艳, 邵虎. 两个带重启方向的改进 HS 型共轭梯度法[J]. 数学物理学报, 2023, 43(2): 570-580.
Liu Pengjie, Wu Yanqiang, Shao Feng, Zhang Yan, Shao Hu. Two Extended HS-type Conjugate Gradient Methods with Restart Directions[J]. Acta mathematica scientia,Series A, 2023, 43(2): 570-580.
使用本文
| [1] |
Hestenes M R, Stiefel E. Methods of conjugate gradients for solving linear systems. Journal of Research of the National Bureau of Standards, 1952, 49(6): 409-436
doi: 10.6028/jres.049.044 |
| [2] | Fletcher R, Reeves C M. Function minimization by conjugate gradients. Computer Journal, 1964, 7(2): 149-154 |
| [3] | Polak E, Ribière G. Note sur la convergence de méthodes de directions conjuées. Revue Française Informatique Et De Recherche Opérationnelle, 1969, 3(16): 35-43 |
| [4] | Polyak B T. The conjugate gradient method in extremal problems. USSR Computational Mathematics and Mathematical Physics, 1969, 9(4): 94-112 |
| [5] |
Dai Y H, Yuan Y X. A nonlinear conjugate gradient method with a strong global convergence property. SIAM Journal on Optimization, 1999, 10(1): 177-182
doi: 10.1137/S1052623497318992 |
| [6] |
Yao S W, Wei Z X, Huang H. A note about WYL's conjugate gradient method and its application. Applied Mathematics and Computation, 2007, 191(2): 381-388
doi: 10.1016/j.amc.2007.02.094 |
| [7] |
Zhang L. An improved Wei-Yao-Liu nonlinear conjugate gradient method for optimization computation. Applied Mathematics and Computation, 2009, 215(6): 2269-2274
doi: 10.1016/j.amc.2009.08.016 |
| [8] | 江羡珍, 马国栋, 简金宝. Wolfe 线搜索下一个新的全局收敛共轭梯度法. 工程数学学报, 2011, 28(6): 779-786 |
| Jiang X Z, Ma G D, Jian J B. A new globally convergent conjugate gradient method with Wolfe line search. Chinese Journal of Engineering Mathematics, 2011, 28(6): 779-786 | |
| [9] | Zhu Z B, Zhang D D, Wang S. Two modified DY conjugate gradient methods for unconstrained optimization problems. Applied Mathematics and Computation, 2020, 373( 15): 125004 |
| [10] |
Jiang X Z, Jian J B, Song D, Liu P J. An improved Polak-Ribière-Polyak conjugate gradient method with an efficient restart direction. Computational and Applied Mathematics, 2021, 40(174): 1-24
doi: 10.1007/s40314-020-01383-5 |
| [11] |
Kou C X, Dai Y H. A modified self-scaling memoryless Broyden-Fletcher-Goldfarb-Shanno method for unconstrained optimization. Journal of Optimization Theory and Applications, 2015, 165: 209-224
doi: 10.1007/s10957-014-0528-4 |
| [12] |
Jian J B, Han L, Jiang X Z. A hybrid conjugate gradient method with descent property for unconstrained optimization. Applied Mathematical Modelling, 2015, 39(3/4): 1281-1290
doi: 10.1016/j.apm.2014.08.008 |
| [13] |
Dai Z F, Wen F H. Another improved Wei-Yao-Liu nonlinear conjugate gradient method with sufficient descent property. Applied Mathematics and Computation, 2012, 218(14): 7421-7430
doi: 10.1016/j.amc.2011.12.091 |
| [14] |
江羡珍, 韩麟, 简金宝. Wolfe 线搜索下一个全局收敛的混合共轭梯度法. 计算数学, 2012, 34(1): 103-112
doi: 10.12286/jssx.2012.1.103 |
|
Jiang X Z, Han L, Jian J B. A new globally convergent mixed conjugate gradient method with Wolfe line search. Mathematica Numerica Sinica, 2012, 34(1): 103-112
doi: 10.12286/jssx.2012.1.103 |
|
| [15] |
简金宝, 刘鹏杰, 江羡珍. 一个充分下降的谱三项共轭梯度法. 应用数学学报, 2020, 43(6): 1000-1012
doi: 10.12387/C2020073 |
|
Jian J B, Liu P J, Jiang X Z. A spectral three-term conjugate gradient method with sufficient descent property. Acta Mathematicae Applicatae Sinica, 2012, 43(6): 1000-1012
doi: 10.12387/C2020073 |
|
| [16] |
Jiang X Z, Jian J B. Improved Fletcher-Reeves and Dai-Yuan conjugate gradient methods with the strong Wolfe line search. Journal of Computational and Applied Mathematics, 2019, 348: 525-534
doi: 10.1016/j.cam.2018.09.012 |
| [17] |
Liu Y F, Zhu Z B, Zhang B X. Two sufficient descent three-term conjugate gradient methods for unconstrained optimization problems with applications in compressive sensing. Journal of Applied Mathematics and Computing, 2022, 68: 1787-1816
doi: 10.1007/s12190-021-01589-8 |
| [18] |
Jiang X Z, Liao W, Yin J H, Jian J B. A new family of hybrid three-term conjugate gradient methods with applications in image restoration. Numerical Algorithms, 2022, 91: 161-191
doi: 10.1007/s11075-022-01258-2 |
| [19] | 朱志斌, 耿远航. 一个改进的 WYL 型三项共轭梯度法. 数学物理学报, 2021, 41A(6): 1871-1879 |
| Zhu Z B, Geng Y H. An modified three-term WYL conjugate gradient method. Acta Mathematica Scientia, 2021, 41A(6): 1871-1879 | |
| [20] | 马国栋. 强 Wolfe 线搜索下的修正 PRP 和 HS 共轭梯度法. 数学物理学报, 2021, 41A(3): 837-847 |
| Ma G D. Improved PRP and HS conjugate gradient methods with strong Wolfe line search. Acta Mathematica Scientia, 2021, 41A(3): 837-847 | |
| [21] | 江羡珍, 廖伟, 简金宝, 毋晓迪. 一个带重启步的改进 PRP 型谱共轭梯度法. 数学物理学报, 2022, 42A(1): 216-227 |
| Jiang X Z, Liao W, Jian J B, Wu X D. An improved PRP type spectral conjugate gradient method with restart steps. Acta Mathematica Scientia, 2022, 42A(1): 216-227 | |
| [22] | 袁功林, 吴宇伦, Pham H. 基于非单调线搜索的 HS-DY 形共轭梯度方法及在图像恢复中的应用. 数学物理学报, 2022, 42A(2): 605-620 |
| Yuan G L, Wu Y L, Pham H. A modified HS-DY-type method with nonmonotone line search for image restoration and unconstrained optimization problems. Acta Mathematica Scientia, 2022, 42A(2): 605-620 | |
| [23] | Yuan G L, Zhou Y J, Zhang M X. A hybrid conjugate gradient algorithm for nonconvex functions and its applications in image restoration problems. Journal of the Operations Research Society of China, 2022, https://doi.org/10.1007/s40305-022-00424-6 |
| [24] | Zoutendijk G. Nonlinear programming computational methods//Abadie J. ed Integer and Nonlinear Programming. Amsterdam: North-Holland, 1970: 37-86 |
| [25] |
Gould N I M, Orban D, Toint P L. CUTEr and SifDec: A constrained and unconstrained testing environment, revisited. ACM Transactions on Mathematical Software, 2003, 29(4): 373-394
doi: 10.1145/962437.962439 |
| [26] |
Moré J J, Garbow B S, Hillstrome K E. Testing unconstrained optimization software. ACM Transactions on Mathematical Software, 1981, 7: 17-41
doi: 10.1145/355934.355936 |
| [27] | Andrei N. An unconstrained optimization test functions collection. Advanced Modeling and Optimization, 2008, 10(1): 147-161 |
| [28] |
Dolan E D, Moré J J. Benchmarking optimization software with performance profiles. Mathematical Programming, 2002, 91(2): 201-213
doi: 10.1007/s101070100263 |
| [1] | 潘庭葳,贺素香. 双重稀疏约束优化问题的一种贪婪单纯形算法[J]. 数学物理学报, 2022, 42(3): 920-933. |
| [2] | 袁功林,吴宇伦,PhamHongtruong. 基于非单调线搜索的HS-DY形共轭梯度方法及在图像恢复中的应用[J]. 数学物理学报, 2022, 42(2): 605-620. |
| [3] | 江羡珍,廖伟,简金宝,毋晓迪. 一个带重启步的改进PRP型谱共轭梯度法[J]. 数学物理学报, 2022, 42(1): 216-227. |
| [4] | 朱志斌,耿远航. 一个改进的WYL型三项共轭梯度法[J]. 数学物理学报, 2021, 41(6): 1871-1879. |
| [5] | 马国栋. 强Wolfe线搜索下的修正PRP和HS共轭梯度法[J]. 数学物理学报, 2021, 41(3): 837-847. |
| [6] | 刘月园,王凯,秦树娟,李姣芬. 列正交约束下广义Sylvester方程极小化问题的有效算法[J]. 数学物理学报, 2021, 41(2): 479-495. |
| [7] | 杨柳,邓醉茶. 退化抛物型方程的一个初值反演问题[J]. 数学物理学报, 2020, 40(4): 891-903. |
| [8] | 马国栋. 一般约束极大极小优化问题一个强收敛的广义梯度投影算法[J]. 数学物理学报, 2020, 40(3): 641-649. |
| [9] | 李向利,师娟娟,董晓亮. 一类修正的非单调谱共轭梯度法及其在非负矩阵分解中的应用[J]. 数学物理学报, 2018, 38(5): 954-962. |
| [10] | 宋卫红, 张凯院, 聂玉峰. 离散对偶代数Riccati方程异类约束解的双迭代算法[J]. 数学物理学报, 2014, 34(6): 1440-1449. |
| [11] | 胡朝明, 万中, 王旭. 一种新的非单调谱共轭梯度算法[J]. 数学物理学报, 2013, 33(1): 78-88. |
| [12] | 周长银; 贺国平; 王永丽. 基于有效约束识别技术的一个SSLE算法及其收敛性分析[J]. 数学物理学报, 2007, 27(3): 535-540. |
| [13] | 王长钰;宇振盛. 求解非线性系统的有效集信赖域方法[J]. 数学物理学报, 2006, 26(2): 223-232. |
| [14] | 时贞军. 精确搜索下的非线性共轭梯度法[J]. 数学物理学报, 2004, 4(6): 675-682. |
| [15] | 高自友, 任华玲, 贺国平. 无严格互补松驰条件的序列线性方程组新算法[J]. 数学物理学报, 2004, 24(3): 275-284. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 216
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 141
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|