一维具有阻尼和摩擦项的可压缩流体欧拉方程组当压力消失时黎曼解的极限

摘要/Abstract

摘要：

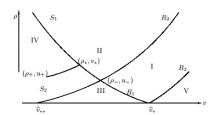
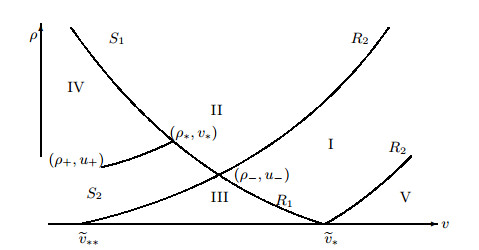
该文研究带有复合源项的一维可压缩流体欧拉方程组的黎曼问题, 其中源项可以是摩擦项, 也可以是阻尼项, 也可以是阻尼和摩擦两者都具有. 与齐次型不同, 非齐次守恒律方程组的黎曼解是非自相似的. 当绝热指数$ \gamma\rightarrow1$即压力消失时, 讨论带有复合源项的一维可压缩流体欧拉方程组的黎曼解中集中现象和真空状态的形成, 证明包含两条激波的黎曼解收敛于零压下的delta激波解, 包含两条稀疏波的黎曼解收敛于零压下的两条接触间断解, 其中连接两条接触间断解的中间状态是真空状态.

关键词: 消失压力极限, 可压缩流体欧拉方程组, 复合源项, Delta激波, 真空状态, 黎曼问题

Abstract:

In this paper, we study the Riemann problem for the Euler equations of compressible fluid flow with a composite source term. The source can cover a Coulomb-like friction or a damping or both. Different from the homogeneous system, Riemann solutions of the inhomogeneous system are non self-similar. Concentration and cavitation in the pressureless limit of solutions to the Riemann problem for the Euler equations of compressible fluid flow with a composite source term are investigated in detail as the adiabatic exponent tends to one. We rigorously proved that, as the adiabatic exponent tends to one, any two-shock Riemann solution tends to a delta shock solution of the pressureless Euler system with a composite source term, and the intermediate density between the two shocks tends to a weighted $ \delta$-mesaure which forms the delta shock; while any two-rarefaction-wave Riemann solution tends to a two-contact-discontinuity solution of the pressureless Euler system with a composite source term, whose intermediate state between the two contact discontinuities is a vacuum state.

Key words: Pressureless limit, Euler equations of compressible fluid flow, Composite source term, Delta shock wave, Vacuum state, Riemann problem

中图分类号:

O175.29

邵志强. 一维具有阻尼和摩擦项的可压缩流体欧拉方程组当压力消失时黎曼解的极限[J]. 数学物理学报, 2022, 42(4): 1150-1172.

Zhiqiang Shao. Concentration and Cavitation in the Pressureless Limit of Euler Equations of Compressible Fluid Flow with Damping and Friction[J]. Acta mathematica scientia,Series A, 2022, 42(4): 1150-1172.

图/表 1

参考文献 60

1	Chaplygin S . On gas jets. Sci Mem Moscow Univ Math Phys, 1904, 21: 1- 121
2	Tsien H S . Two dimensional subsonic flow of compressible fluids. J Aeron Sci, 1939, 6: 399- 407 doi: 10.2514/8.916
3	Von Karman T . Compressibility effects in aerodynamics. J Aeron Sci, 1941, 8: 337- 356 doi: 10.2514/8.10737
4	Shen C . The Riemann problem for the pressureless Euler system with the Coulomb-like friction term. IMA J Appl Math, 2016, 81: 76- 99
5	Faccanoni G , Mangeney A . Exact solution for granular flows. Int J Numer Anal Meth Geomech, 2012, 37: 1408- 1433
6	Earnshaw S . On the mathematical theory of sound. Philos Trans, 1858, 150: 1150- 1154
7	Lu Y G . Existence of global entropy solutions to a nonstrictly hyperbolic system. Arch Ration Mech Anal, 2005, 178: 287- 299 doi: 10.1007/s00205-005-0379-0
8	Cheng Z . Global entropy solutions to a variant of the compressible Euler equations. Appl Math Lett, 2008, 21: 410- 415 doi: 10.1016/j.aml.2007.03.022
9	Klainerman S , Majda A . Singular limits of quasilinear hyperbolic systems with large parameters and the incompressible limit of compressible fluids. Comm Pure Appl Math, 1981, 34: 481- 524 doi: 10.1002/cpa.3160340405
10	Oelschläger K . On the connection between Hamiltonian many-particle systems and the hydrodynamical equation. Arch Ration Mech Anal, 1991, 115: 297- 310 doi: 10.1007/BF00375277
11	Oelschläger K . An integro-differential equation modelling a Newtonian dynamics and its scaling limit. Arch Ration Mech Anal, 1997, 137: 99- 134 doi: 10.1007/s002050050024
12	Caprino S , Esposito R , Marra R , Pulvirenti M . Hydrodynamic limits of the Vlasov equation. Comm Partial Differential Equations, 1993, 18: 805- 820 doi: 10.1080/03605309308820951
13	Cheng H , Yang H , Zhang Y . Riemann problem for the Chaplygin Euler equations of compressible fluid flow. Int J Nonlinear Sci Numer Simul, 2010, 11: 985- 992
14	DiPerna R J . Global solutions to a class of nonlinear hyperbolic systems of equations. Comm Pure Appl Math, 1973, 26: 1- 28 doi: 10.1002/cpa.3160260102
15	Li C Z . Existence in the large for certain systems of quasi linear hyperbolic conservation laws. J Differential Equations, 1982, 45: 85- 102 doi: 10.1016/0022-0396(82)90056-0
16	Pang Y , Zhang Y , Wen Y . Delta shock wave to the compressible fluid flow with the generalized Chaplygin gas. Int J Nonlinear Mech, 2018, 99: 311- 318 doi: 10.1016/j.ijnonlinmec.2017.12.014
17	Sarrico C O R , Paiva A . The multiplication of distributions in the study of a Riemann problem in fluid dynamics. J Nonlinear Math Phys, 2017, 24: 328- 345
18	Song G , Xiao J . Existence of global weak solutions to a special system of Euler equation with a source (Ⅱ): General case. J Math Anal Appl, 2009, 352: 943- 953 doi: 10.1016/j.jmaa.2008.11.051
19	Sheng S , Shao Z . Concentration of mass in the pressureless limit of the Euler equations of one-dimensional compressible fluid flow. Nonlinear Analysis: Real World Applications, 2020, 52: 103039 doi: 10.1016/j.nonrwa.2019.103039
20	Sheng S , Shao Z . The limits of Riemann solutions to Euler equations of compressible fluid flow with a source term. Journal of Engineering Mathematics, 2020, 125: 1- 22 doi: 10.1007/s10665-020-10066-3
21	Savage S B , Hutter K . The motion of a finite mass of granular material down a rough incline. J Fluid Mech, 1989, 199: 177- 215 doi: 10.1017/S0022112089000340
22	Shen C . The Riemann problem for the Chaplygin gas equations with a source term. Z Angew Math Mech, 2016, 96: 681- 695 doi: 10.1002/zamm.201500015
23	Sun M . The exact Riemann solutions to the generalized Chaplygin gas equations with friction. Commun Nonlinear Sci Numer Simul, 2016, 36: 342- 353 doi: 10.1016/j.cnsns.2015.12.013
24	Daw D A E , Nedeljkov M . Shadow waves for pressureless gas balance laws. Appl Math Lett, 2016, 57: 54- 59 doi: 10.1016/j.aml.2016.01.004
25	Edwards C M , Howison S D , Ockendon H , Ockendon J R . Non-classical shallow water flows. IMA J Appl Math, 2008, 73: 137- 157
26	Guo L , Li T , Yin G . The limit behavior of the Riemann solutions to the generalized Chaplygin gas equations with a source term. J Math Anal Appl, 2017, 455: 127- 140 doi: 10.1016/j.jmaa.2017.05.048
27	Guo L , Li T , Yin G . The vanishing pressure limits of Riemann solutions to the Chaplygin gas equations with a source term. Commun Pure Appl Anal, 2017, 16: 295- 309 doi: 10.3934/cpaa.2017014
28	Zhang Y , Zhang Y . Riemann problems for a class of coupled hyperbolic systems of conservation laws with a source term. Commun Pure Appl Anal, 2019, 18: 1523- 1545 doi: 10.3934/cpaa.2019073
29	Zhang Y , Zhang Y . The Riemann problem for the Suliciu relaxation system with the double-coefficient Coulomb-like friction terms. Int J Non-Linear Mech, 2019, 116: 200- 210 doi: 10.1016/j.ijnonlinmec.2019.07.004
30	Zhang Y , Zhang Y , Wang J . Zero-exponent limit to the extended Chaplygin gas equations with friction. Bull Malays Math Sci Soc, 2021, 44: 3571- 3599 doi: 10.1007/s40840-021-01133-8
31	Zhang Q . Concentration in the flux approximation limit of Riemann solutions to the extended Chaplygin gas equations with friction. J Math Phys, 2019, 60: 101508 doi: 10.1063/1.5085233
32	Yin G , Chen J . Existence and stability of Riemann solution to the Aw-Rascle model with friction. Indian J Pure Appl Math, 2018, 49: 671- 688 doi: 10.1007/s13226-018-0294-3
33	Sheng S , Shao Z . The vanishing adiabatic exponent limits of Riemann solutions to the isentropic Euler equations for power law with a Coulomb-like friction term. J Math Phys, 2019, 60: 101504 doi: 10.1063/1.5108863
34	Bourgault Y , Habashi W G , Dompierre J , Baruzzi G S . A finite element method study of Eulerian droplets impingement models. Internat. J Numer Methods Fluids, 1999, 29: 429- 449 doi: 10.1002/(SICI)1097-0363(19990228)29:4<429::AID-FLD795>3.0.CO;2-F
35	Boutanios Z, Bourgault Y, Cober S, et al. 3D droplets impingement analysis around an aircraft's nose and cockpit using FENSAP-ICE[C]//36th AIAA Aerospace Science Meeting and Exhibit, Reno, NV, USA, 1998. DOI: 10.2514/6.1998-200
36	Bourgault Y, Thiriet M. Critical aspects of flow and aerosol simulations in the airway tract[C]//European Conference on Computational Fluid Dynamics-ECCOMAS CFD 2008, Venice, Italy, 2008
37	Keita S , Bourgault Y . Eulerian droplet model: Delta-shocks and solution of the Riemann problem. J Math Anal Appl, 2019, 472: 1001- 1027 doi: 10.1016/j.jmaa.2018.11.061
38	Bourgault Y. Computing gas-particle flows in airways with an Eulerian model[C]//European Conference on Computational Fluid Dynamics - ECCOMAS CFD 2006, Egmond ann Zee, The Netherlands, 2006
39	Keita S , Bourgault Y . Eulerian models with particle pressure for air-particle flows. European Journal of Mechanics-/B Fluids, 2019, 78: 263- 275 doi: 10.1016/j.euromechflu.2019.08.001
40	Chen G Q , Liu H . Formation of δ -shocks and vacuum states in the vanishing pressure limit of solutions to the Euler equations for isentropic fluids. SIAM J Math Anal, 2003, 34: 925- 938 doi: 10.1137/S0036141001399350
41	Chen G Q , Liu H . Concentration and cavitation in the vanishing pressure limit of solutions to the Euler equations for nonisentropic fluids. Phys D, 2004, 189: 141- 165 doi: 10.1016/j.physd.2003.09.039
42	Li J . Note on the compressible Euler equations with zero temperature. Appl Math Lett, 2001, 14: 519- 523 doi: 10.1016/S0893-9659(00)00187-7
43	Ibrahim M , Liu F , Liu S . Concentration of mass in the pressureless limit of Euler equations for power law. Nonlinear Anal Real World Appl, 2019, 47: 224- 235 doi: 10.1016/j.nonrwa.2018.10.015
44	Li H , Shao Z . Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for generalized Chaplygin gas. Commun Pure Appl Anal, 2016, 15: 2373- 2400 doi: 10.3934/cpaa.2016041
45	Shen C . The limits of Riemann solutions to the isentropic magnetogasdynamics. Appl Math Lett, 2011, 24: 1124- 1129 doi: 10.1016/j.aml.2011.01.038
46	Shen C , Sun M . Formation of delta shocks and vacuum states in the vanishing pressure limit of Riemann solutions to the perturbed Aw-Rascle model. J Differential Equations, 2010, 249: 3024- 3051 doi: 10.1016/j.jde.2010.09.004
47	Shen C , Sun M , Wang Z . Limit relations for three simple hyperbolic systems of conservation laws. Math Methods Appl Sci, 2010, 33: 1317- 1330 doi: 10.1002/mma.1248
48	Sun M . Concentration and cavitation phenomena of Riemann solutions for the isentropic Euler system with the logarithmic equation of state. Nonlinear Anal Real World Appl, 2020, 53: 103068 doi: 10.1016/j.nonrwa.2019.103068
49	Tong M , Shen C . The limits of Riemann solutions for the isentropic Euler system with extended Chaplygin gas. Applicable Analysis, 2019, 98: 2668- 2687 doi: 10.1080/00036811.2018.1469009
50	Sheng W , Wang G , Yin G . Delta wave and vacuum state for generalized Chaplygin gas dynamics system as pressure vanishes. Nonlinear Anal Real World Appl, 2015, 22: 115- 128 doi: 10.1016/j.nonrwa.2014.08.007
51	Sun M . The limits of Riemann solutions to the simplified pressureless Euler system with flux approximation. Math Methods Appl Sci, 2018, 41: 4528- 4548 doi: 10.1002/mma.4912
52	Yang H , Wang J . Delta shocks and vacuum states in vanishing pressure limits of solutions to the isentropic Euler equations for modified Chaplygin gas. J Math Anal Appl, 2014, 413: 800- 820 doi: 10.1016/j.jmaa.2013.12.025
53	Yang H , Zhang Y . Flux approximation to the isentropic relativistic Euler equations. Nonlinear Anal, 2016, 133: 200- 227 doi: 10.1016/j.na.2015.12.002
54	Yin G , Sheng W . Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for polytropic gases. J Math Anal Appl, 2009, 355: 594- 605 doi: 10.1016/j.jmaa.2009.01.075
55	Yin G , Sheng W . Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations. Chin Ann Math, 2008, 29B: 611- 622
56	Yin G , Sheng W . Delta wave formation and vacuum state in vanishing pressure limit for system of conservation laws to relativistic fluid dynamics. Z Angew Math Mech, 2015, 95: 49- 65 doi: 10.1002/zamm.201200148
57	Zhang Y , Yang H . Flux-approximation limits of solutions to the relativistic Euler equations for polytropic gas. J Math Anal Appl, 2016, 435: 1160- 1182 doi: 10.1016/j.jmaa.2015.11.012
58	Zhang Y , Zhang Y . Delta-shocks and vacuums in the relativistic Euler equations for isothermal fluids with the flux approximation. J Math Phys, 2019, 60: 011508
59	Sheng W, Zhang T. The Riemann Problem for the Transportation Equations in Gas Dynamics. Providence, RI: Amer Math Soc, 1999
60	Joseph K T . A Riemann problem whose viscosity solutions contain delta measures. Asymptot Anal, 1993, 7: 105- 120

[1]	陈雨风,陈停停,王振. 非等熵Chaplygin气体测度值解存在性[J]. 数学物理学报, 2020, 40(4): 833-841.
[2]	张庆玲,巴英. 带群集耗散项的零压流方程的扰动黎曼问题[J]. 数学物理学报, 2020, 40(1): 49-62.
[3]	潘丽君,韩欣利,李彤. 色谱方程的广义黎曼问题:含有Delta激波[J]. 数学物理学报, 2019, 39(6): 1300-1313.
[4]	李华惠, 邵志强. 压力消失时具有广义Chaplygin气体的Aw-Rascle交通模型Riemann解的极限[J]. 数学物理学报, 2017, 37(5): 917-930.
[5]	李华惠, 邵志强. 用分离的Delta函数法研究非对称Keyfitz-Kranzer系统中Delta激波的交互性[J]. 数学物理学报, 2017, 37(4): 714-729.
[6]	陆云光, 宣本金. 一组双曲型方程组的Riemann问题[J]. 数学物理学报, 1996, 16(2): 187-194.