基于迭代学习算法的偏微分多智能体系统的包容控制

摘要/Abstract

摘要：

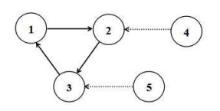
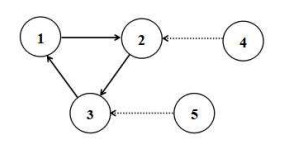
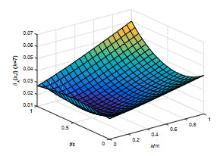
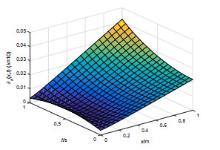
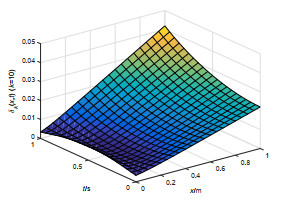
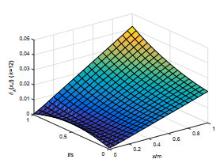
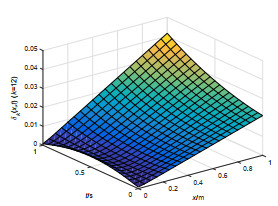
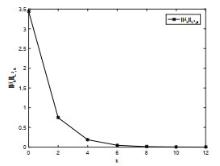
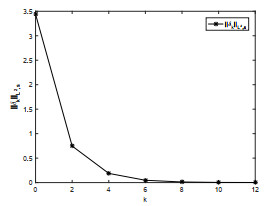
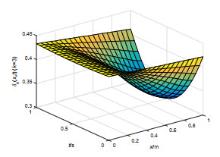
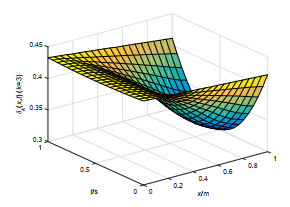
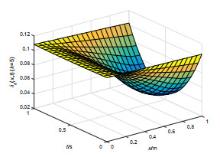
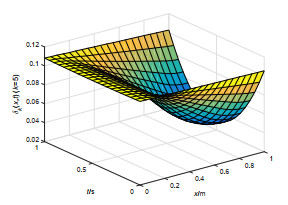
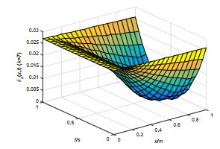
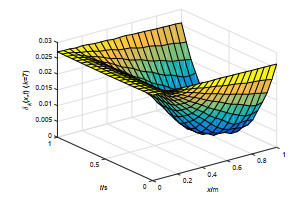
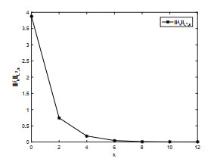
该文研究一类偏微分多智能体系统的包容控制问题，该类系统是由二阶抛物型或二阶双曲型偏微分方程构建而成.基于网络拓扑结构，依据跟随者系统的输出形式，设计了P型迭代学习律，得到了系统基于迭代学习稳定性意义下的收敛性条件.利用压缩映射原理，证明了两类系统的包容误差在有限时间区间内随迭代次数的增加于L²空间中收敛到零.最后，仿真算例验证了理论分析的正确性.

关键词: 迭代学习算法, 偏微分方程, 多智能体系统, 包容控制

Abstract:

In this paper, we deals with the containment control problem for a class of partial differential multi-agent systems, which are composed of the second-order parabolic equations or the second-order hyperbolic equations. Based on the framework of network topologies, the P-type iterative learning law is designed depending on the output form of the follower system, and the convergence condition of the system in the sense of iterative learning stability is obtained. By using the contraction mapping method, it is proved that the containment errors of two kinds of systems on the finite time interval converge to zero on $L^2$ space with the increasing of iterations. Finally, simulation examples demonstrate the validity of the theoretical analysis.

Key words: Iterative learning algorithm, Partial differential equation, Multi-agent systems, Containment control

中图分类号:

TP13

张丹,傅勤,陈振杰. 基于迭代学习算法的偏微分多智能体系统的包容控制[J]. 数学物理学报, 2021, 41(4): 1111-1123.

Dan Zhang,Qin Fu,Zhenjie Chen. Containment Control for Partial Differential Multi-Agent Systems via Iterative Learning Algorithm[J]. Acta mathematica scientia,Series A, 2021, 41(4): 1111-1123.

图/表 9

图 1

图 2

图 3

图 4

图 5

图 6

图 7

图 8

图 9

参考文献 30

1	Fang C , Zhou Z Y , Zhao P , Lin Z C . Feature learning via partial differential equation with applications to face recognition. Pattern Recognition, 2017, 69, 14- 25 doi: 10.1016/j.patcog.2017.03.034
2	Acevedo J I , Lelievre T . A nonlinear approximation method for solving high dimensional partial differential equations: Application in finance. Mathematics and Computers in Simulation, 2018, 143, 14- 34 doi: 10.1016/j.matcom.2016.07.013
3	Tian C , Chang K C , Chen J S . Application of hyperbolic partial differential equations in global optimal scheduling of UAV. Alexandria Engineering Journal, 2020, 59 (4): 2283- 2289 doi: 10.1016/j.aej.2020.02.013
4	樊晓平, 徐建闽, 周其节, 梁天培. 柔性机器人的动力学建模及控制. 控制理论与应用, 1997, 14 (3): 318- 335
	Fan X P , Xu J M , Zhou Q J , Liang T P . Dynamic modeling and control of flexible robotic manipulators. Control Theory and Applications, 1997, 14 (3): 318- 335
5	Selvadurai A P S . Partial Differential Equations in Mechanics 1:Fundamentals, Laplace's Equation, Diffusion Equations, Wave Equations. Berlin: Springer, 2000
6	Lapidus L , Pinder G F . Numerical Solution of Partial Differential Equations in Science and Engineering. New York: John Wiley & Sons Inc, 1982
7	Arimoto S , Kawamura S , Miyazaki F . Bettering operation of robots by learning. Journal of Robotic Systems, 1984, 1 (2): 123- 140 doi: 10.1002/rob.4620010203
8	Dai X S , Tian S P , Peng Y J , Luo W G . Closed-loop P-type iterative learning control of uncertain linear distributed parameter systems. IEEE/CAA Journal of Automatica Sinica, 2014, 1 (3): 267- 273 doi: 10.1109/JAS.2014.7004684
9	傅勤. 非正则分布参数系统的迭代学习控制. 控制与决策, 2016, 31 (1): 114- 122
	Fu Q . Iterative learning control for irregular distributed parameter systems. Control and Decision, 2016, 31 (1): 114- 122
10	Meryem H , Cheng S , Samia H . A PD-type iterative learning control algorithm for one-dimension linear wave equation. International Journal of Control, Automation and Systems, 2020, 18 (4): 1045- 1052 doi: 10.1007/s12555-019-0094-5
11	Fu Q , Gu P P , Wu J R . Iterative learning control for one-dimensional fourth order distributed parameter systems. Science China Information Sciences, 2017, 60 (1): 012204 doi: 10.1007/s11432-015-1031-6
12	Gao R , Huang J S , Wang L . Leaderless consensus control of uncertain multi-agent systems with sensor and actuator attacks. Information Sciences, 2019, 505, 144- 156 doi: 10.1016/j.ins.2019.07.075
13	Liu Y , Hou X H . Event-triggered consensus control of disturbed multi-agent systems using output feedback. ISA Transactions, 2019, 91, 166- 173 doi: 10.1016/j.isatra.2019.02.004
14	Han J , Zhang H G , Jiang H , Sun X . ${H_∞}$ Consensus for linear heterogenerous multi-agent systems with state and output feedback. Neurocomputing, 2018, 275 (31): 2635- 2644
15	Gao J F , Zheng M N . Distributed adaptive event-triggered protocol for tracking control of leader-following multi-agent systems. Journal of the Franklin Institute, 2019, 356 (17): 10466- 10479 doi: 10.1016/j.jfranklin.2018.07.019
16	Jenabzadeh A , Safarinejadian B . Distributed estimation and control for nonlinear multi-agent systems in the presence of input delay or external disturbances. ISA Transactions, 2020, 98, 198- 206 doi: 10.1016/j.isatra.2019.08.059
17	Xiao W B , Cao L , Li H Y , Lu R Q . Observer-based adaptive consensus control for nonlinear multi-agent systems with time-delay. Science China Information Sciences, 2020, 63, 132202 doi: 10.1007/s11432-019-2678-2
18	Zou W C , Xiang Z R . Event-triggered leader-following consensus of non-linear multi-agent systems with switched dynamics. IET Control Theory and Applications, 2019, 13 (9): 1222- 1228 doi: 10.1049/iet-cta.2018.5126
19	Dong X W , Meng F L , Shi Z Y , et al. Output containment control for swarm systems with general linear dynamics: A dynamic output feedback approach. Systems and Control Letters, 2014, 71, 31- 37 doi: 10.1016/j.sysconle.2014.06.007
20	Zhou F , Wang Z J . Containment control of linear multi-agent systems with directed graphs and multiple leaders of time-varying bounded inputs. IET Control Theory and Applications, 2015, 9 (16): 2466- 2473 doi: 10.1049/iet-cta.2014.0634
21	Zou W C , Xiang Z R . Event-triggered distributed containment control of heterogeneous linear multi-agent systems by an output regulation approach. International Journal of Systems Science, 2017, 48 (10): 2041- 2054 doi: 10.1080/00207721.2017.1309595
22	Zou W C , Xiang Z R . Event-triggered containment control of second-order nonlinear multi-agent systems. Journal of the Franklin Institute, 2019, 356 (17): 10421- 10438 doi: 10.1016/j.jfranklin.2018.05.060
23	Lu H , He W L , Han Q L , et al. Finite-time containment control for nonlinear multi-agent systems with external disturbances. Information Sciences, 2020, 512, 338- 351 doi: 10.1016/j.ins.2019.05.049
24	Fu Q , Du L L , Xu G Z , Wu J R , Yu P F . Consensus control for multi-agent systems with distributed parameter models. Neurocomputing, 2018, 308 (25): 58- 64
25	Fu Q , Yu P F , Xu G Z . Containment control for partial differerntial multi-agent systems. Physica A, 2019, 529 (01): 121549: 11
26	Fu Q , Du L L , Xu G Z , Wu J R . Consensus control for multi-agent systems with distributed parameter models via iterative learning algorithm. Journal of the Franklin Institute, 2018, 355 (10): 4453- 4472
27	Dai X S , Wang C , Tian S P , Huang Q N . Consensus control via iterative learning for distributed parameter models multi-agent systems with time-delay. Journal of the Franklin Institute, 2019, 356 (10): 5240- 5259
28	郁鹏飞, 傅勤, 陈振杰, 张丹. 四阶偏微分多智能体系统的迭代学习控制. 数学物理学报, 2020, 40A (4): 1029- 1042 doi: 10.3969/j.issn.1003-3998.2020.04.018
	Yu P F , Fu Q , Chen Z J , Zhang D . Iterative learning control for fourth order partial differential multi-agent systems. Acta Mathematica Scientia, 2020, 40A (4): 1029- 1042 doi: 10.3969/j.issn.1003-3998.2020.04.018
29	Fu Q . Iterative learning control for nonlinear heterogeneous multi-agent systems with multiple leaders. Transactions of the Institute of Measurement and Control, 2021, 43 (4): 854- 861 doi: 10.1177/0142331220941636
30	Huang D Q , Xu J X , Li X F , et al. D-type anticipatory iterative learning control for a class of inhomogeneous heat equations. Automatica, 2013, 49 (8): 2397- 2408 doi: 10.1016/j.automatica.2013.05.005

[1]	赵辉艳,徐嗣棪. 一类时间变换的强马氏过程[J]. 数学物理学报, 2021, 41(3): 848-859.
[2]	郁鹏飞,傅勤. 四阶偏微分多智能体系统的迭代学习控制[J]. 数学物理学报, 2020, 40(4): 1029-1042.
[3]	盖彦荣, 齐耀辉, 陈阳舟, 宋学君. 高阶离散时间多智能体系统的量化一致性[J]. 数学物理学报, 2017, 37(6): 1176-1188.
[4]	熊君, 李俊民, 何超. 一阶双曲型偏微分方程的模糊边界控制[J]. 数学物理学报, 2017, 37(3): 469-477.
[5]	马晴霞, 刘安平. 脉冲时滞中立双曲型方程组的振动性[J]. 数学物理学报, 2016, 36(3): 462-472.
[6]	娄翠娟, 杨茵. 一类经典趋化性模型行波解的存在性[J]. 数学物理学报, 2015, 35(6): 1044-1058.
[7]	李祥, 李志祥. 一类种群动力学中具有状态选择时滞的非局部偏微分方程的强周期解[J]. 数学物理学报, 2011, 31(3): 709-719.
[8]	高凌云. C^m中高阶偏微分方程的代数体解[J]. 数学物理学报, 2008, 28(5): 856-862.
[9]	冉启康. 一类椭圆型随机偏微分方程弱解的存在性[J]. 数学物理学报, 2008, 28(2): 320-328.
[10]	张宗劳. CH上的方程△u－hu＋fu^p＝０与黎曼度量的共形形变[J]. 数学物理学报, 2002, 22(1): 135-144.
[11]	崔元顺. 一类广义矢量偏微分方程的并矢格林函数解及其应用[J]. 数学物理学报, 1999, 19(1): 17-22.
[12]	郭艾. 一类非线性积分偏微分方程初边值问题的整体解[J]. 数学物理学报, 1999, 19(1): 30-38.
[13]	崔尚斌. 高阶非线性抛物型偏微分方程组的初值问题[J]. 数学物理学报, 1995, 15(2): 209-216.
[14]	李立鹏. 高维变系数线性偏微分方程组Cauchy问题抛物性的新判据[J]. 数学物理学报, 1994, 14(S1): 134-140.
[15]	王存政. 含和不含外力项的KdV和MKdV方程的求解公式及各种类型的解[J]. 数学物理学报, 1990, 10(1): 112-120.