摘要:
该文研究如下Kirchhoff型方程










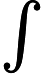







































其中 ,
,  ,
,  都是正常数,
都是正常数,  <
< <
<











 .应用扰动的方法证明了:对于适当的
.应用扰动的方法证明了:对于适当的


 ,存在
,存在
 ,当
,当 <
< <
<
 时,上述问题存在多解.
时,上述问题存在多解.
中图分类号:
梁文翠,张正杰. Kirchhoff型方程有关的非线性方程多解的存在性[J]. 数学物理学报, 2020, 40(4): 842-849.
Wencui Liang,Zhengjie Zhang. Multiple Solutions for Nonlinear Equations Related to Kirchhoff Type Equations[J]. Acta mathematica scientia,Series A, 2020, 40(4): 842-849.