数学物理学报 ›› 2020, Vol. 40 ›› Issue (3): 824-832.
• 论文 • 上一篇
基于Gronwall积分不等式的比例时滞神经网络稳定性分析
- 河池学院计数学与统计学院 广西宜州 546300
-
收稿日期:2018-12-24出版日期:2020-06-26发布日期:2020-07-15 -
通讯作者:罗日才 E-mail:hxs509@163.com;luoricai@163.com;wang4896@126.com -
作者简介:黄星寿, E-mail:hxs509@163.com |王五生, E-mail:wang4896@126.com -
基金资助:国家自然科学基金(11961021);河池学院高层次人才科研项目(2019GCC005)
Stability Analysis for a Class Neural Network with Proportional Delay Based on the Gronwall Integral Inequality
Xingshou Huang( ),Ricai Luo*(
),Ricai Luo*( ),Wusheng Wang(
),Wusheng Wang( )
)
- Department of Mathematics and Statistics, Hechi University, Guangxi Yizhou 546300
-
Received:2018-12-24Online:2020-06-26Published:2020-07-15 -
Contact:Ricai Luo E-mail:hxs509@163.com;luoricai@163.com;wang4896@126.com -
Supported by:the NSFC(11961021);the Hechi University Research Fund for Advanced Talents(2019GCC005)
摘要:
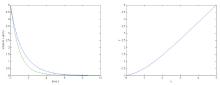
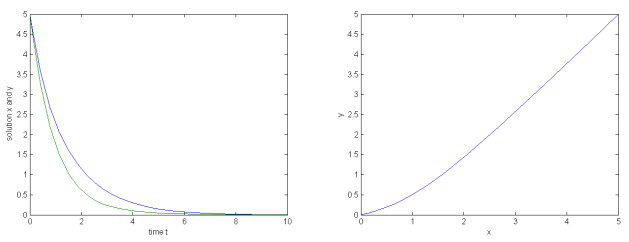
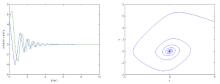
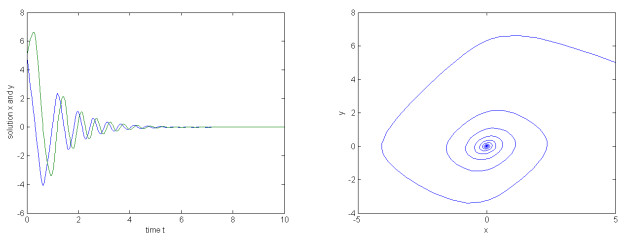
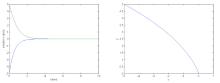
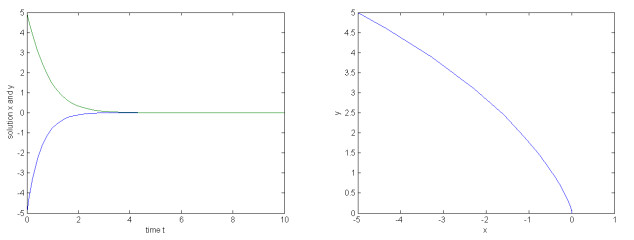
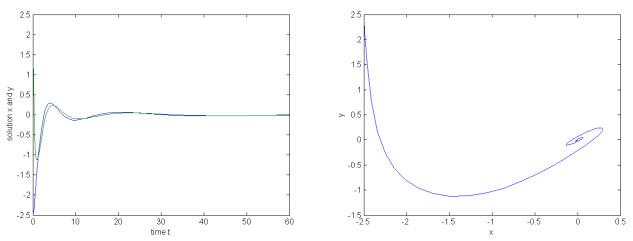
在时滞神经网络的研究中,人们通常是利用构造李亚普诺夫函数来分析系统的稳定性.该文研究了一类具有放缩时滞的神经网络,利用Gronwall积分不等式研究了该放缩时滞神经网络的稳定性问题,得出该系统全局指数稳定性的新判据,并通过实例仿真验证了结果的有效性和可行性.
中图分类号:
- O175
引用本文
黄星寿,罗日才,王五生. 基于Gronwall积分不等式的比例时滞神经网络稳定性分析[J]. 数学物理学报, 2020, 40(3): 824-832.
Xingshou Huang,Ricai Luo,Wusheng Wang. Stability Analysis for a Class Neural Network with Proportional Delay Based on the Gronwall Integral Inequality[J]. Acta mathematica scientia,Series A, 2020, 40(3): 824-832.
使用本文
| 1 |
Ye H , Michel A N , Wang K . Global stability and local stability of Hopfield neural networks with delays. Physical Review E, 1994, 50 (5): 4206- 4213
doi: 10.1103/PhysRevE.50.4206 |
| 2 | Marcus C M , Westervelt R M . Stability of analog neural networks with delay. Physical Review A, 1989, 39 (1): 347- 359 |
| 3 |
Liao X , Liao Y . Stability of Hopfield-type neural networks Ⅱ. Science in China Series A Mathematics, 1997, 40 (8): 813- 816
doi: 10.1007/BF02878920 |
| 4 |
Cao J , Zhou D . Stability analysis of delayed cellular neural networks. Neural Networks, 1998, 11 (9): 1601- 1605
doi: 10.1016/S0893-6080(98)00080-X |
| 5 |
Driessche P , Zou X . Global attractivity in delayed Hopfield neural network models. Society for Industrial and Applied Mathematics, 1998, 58 (6): 1878- 1890
doi: 10.1137/S0036139997321219 |
| 6 | Cao J . Periodic oscillation and exponential stability of delayed CNNs. Physics Letters A, 2000, 270 (3/4): 157- 163 |
| 7 |
Xu D , Zhao H , Zhu H . Global dynamics of Hopfield neural networks involving variable delays. Computers and Mathematics with Applications, 2001, 42, 39- 45
doi: 10.1016/S0898-1221(01)00128-6 |
| 8 |
Chen A , Cao J , Huang L . An estimation of upperbound of delays for global asymptotic stability of delayed Hopfield neural networks. IEEE Transactions on Circuits and Systems I, 2002, 49 (7): 1028- 1032
doi: 10.1109/TCSI.2002.800841 |
| 9 |
Wang L , Xu D . Stability analysis of Hopfield neural networks with time delay. Applied Mathematics and Mechanics, 2002, 23 (1): 65- 70
doi: 10.1007/BF02437731 |
| 10 |
Zhao H , Wang L , Ma C . Hopf bifurcation and stability analysis on discrete-time Hopfield neural network with delay. Nonlinear Analysis Real World Applications, 2008, 9 (1): 103- 113
doi: 10.1016/j.nonrwa.2006.09.005 |
| 11 |
Orman Z . New sufficient conditions for global stability of neutral-type neural networks with time delays. Neurocomputing, 2012, 97, 141- 148
doi: 10.1016/j.neucom.2012.05.016 |
| 12 |
Zhou L . Dissipativity of a class of cellular neural networks with proportional delays. Nonlinear Dynamics, 2013, 73, 1895- 1903
doi: 10.1007/s11071-013-0912-x |
| 13 |
Zhou L , Chen X , Yang Y . Asymptotic stability of cellular neural networks with multiple proportional delays. Applied Mathematics and Computation, 2014, 229, 457- 466
doi: 10.1016/j.amc.2013.12.061 |
| 14 | Zhou L . Global asymptotic stability of cellular neural networks with proportional delays. Nonlinear Dynamics, 2014, 77 (1/2): 41- 47 |
| 15 |
Zheng C , Li N , Cao J . Matrix measure based stability criteria for high-order neural networks with proportional delay. Neurocomputing, 2015, 149, 1149- 1154
doi: 10.1016/j.neucom.2014.09.016 |
| 16 |
Hien L V , Son D T . Finite-time stability of a class of non-autonomous neural networks with heterogeneous proportional delays. Applied Mathematics and Computation, 2015, 251, 14- 23
doi: 10.1016/j.amc.2014.11.044 |
| 17 |
Liu B . Global exponential convergence of non-autonomous cellular neural networks with multi-proportional delays. Neurocomputing, 2016, 191, 352- 355
doi: 10.1016/j.neucom.2016.01.046 |
| 18 | Yu Y . Exponential stability of pseudo almost periodic solutions for cellular neural networks with multi-proportional delays. Neural Processing Letters, 2016, 45 (1): 141- 151 |
| 19 |
Zhou L . Global exponential stability of a class of impulsive recurrent neural networks with proportional delays via fixed point theory. Journal of the Franklin Institute, 2016, 353 (2): 561- 575
doi: 10.1016/j.jfranklin.2015.10.021 |
| 20 |
Xu C , Li P . Global exponential convergence of neutral-type Hopfield neural networks with multi-proportional delays and leakage delays. Chaos, Solitons and Fractals, 2017, 96, 139- 144
doi: 10.1016/j.chaos.2017.01.012 |
| 21 |
Cui N , Jiang H , Hu C , Abdurahman A . Global asymptotic and robust stability of inertial neural networks with proportional delays. Neurocomputing, 2018, 272, 326- 333
doi: 10.1016/j.neucom.2017.07.001 |
| 22 |
Guan K . Global power-rate synchronization of chaotic neural networks with proportional delay via impulsive control. Neurocomputing, 2018, 283, 256- 265
doi: 10.1016/j.neucom.2018.01.027 |
| 23 |
罗日才, 许弘雷, 王五生. 一类新的变时滞中立型神经网络的全局渐近稳定性条件. 数学物理学报, 2015, 35A (3): 634- 640
doi: 10.3969/j.issn.1003-3998.2015.03.017 |
| 24 | 张若军, 王林山. 具有分布时滞的细胞神经网络的概周期解. 数学物理学报, 2011, 31A (2): 422- 429 |
| 25 |
Gronwall T H . Note on the derivatives with respect to a parameter of the solutions of a system of differential equations. Annals of Mathematics, 1919, 20, 292- 296
doi: 10.2307/1967124 |
| 26 |
Bellman R . The stability of solutions of linear differential equations. Duke Mathematical Journal, 1943, 10, 643- 647
doi: 10.1215/S0012-7094-43-01059-2 |
| 27 |
Lipovan O . A retarded Gronwall-like inequality and its applications. Journal of Mathematical Analysis and Applications, 2000, 252, 389- 401
doi: 10.1006/jmaa.2000.7085 |
| 28 |
Abdeldaim A , Yakout M . On some new integral inequalities of Gronwall-Bellman-Pachpatte type. Applied Mathematics and Computation, 2011, 217, 7887- 7899
doi: 10.1016/j.amc.2011.02.093 |
| 29 | Abdeldaim A . Nonlinear retarded integral inequalities of type and applications. Journal of Mathematical Inequalities, 2016, 10 (1): 285- 299 |
| [1] | 邹瑶,曾春娜,胡进. 具有不连续激活函数的复数神经网络的全局指数周期性[J]. 数学物理学报, 2019, 39(5): 1192-1204. |
| [2] | 周庆华,万立,刘杰. 具有变时滞的神经型Hopfield神经网络的全局吸引子研究[J]. 数学物理学报, 2019, 39(4): 823-831. |
| [3] | 熊君, 李俊民, 何超. 一阶双曲型偏微分方程的模糊边界控制[J]. 数学物理学报, 2017, 37(3): 469-477. |
| [4] | 殷春, 周士伟, 吴姗姗, 程玉华, 魏修岭, 王伟. 带有离散分布式延迟神经网络的不等时滞分割稳定性分析方法[J]. 数学物理学报, 2017, 37(2): 374-389. |
| [5] | 张丽萍, 刘东毅, 张国山. 带有内部扰动的Timoshenko梁系统的指数稳定性[J]. 数学物理学报, 2017, 37(1): 185-198. |
| [6] | 阿卜杜杰力力·阿卜杜热合曼, 蒋海军, 滕志东. 具有混合变时滞的脉冲Cohen-Grossberg神经网络的指数同步[J]. 数学物理学报, 2015, 35(3): 545-557. |
| [7] | 罗日才, 许弘雷, 王五生. 一类新的变时滞中立型神经网络的全局渐近稳定性条件[J]. 数学物理学报, 2015, 35(3): 634-640. |
| [8] | 张永全, 李有梅, 曹飞龙, 徐宗本. 高斯核正则化学习算法的泛化误差[J]. 数学物理学报, 2014, 34(5): 1049-1060. |
| [9] | 潘特铁, 时宝, 杨树杰, 张强. 具时滞和脉冲的随机BAM型Cohen-Grossberg神经网络的稳定性分析[J]. 数学物理学报, 2013, 33(5): 937-950. |
| [10] | 张雨田, 罗琦. 具反应扩散项和Neumann边界条件的脉冲变时滞细胞神经网络的全局指数稳定性[J]. 数学物理学报, 2013, 33(4): 777-786. |
| [11] | 章春国. 具有局部记忆阻尼的非均质Timoshenko梁的稳定性[J]. 数学物理学报, 2012, 32(1): 186-200. |
| [12] | 冯春华. 一类简化的n个神经元时滞BAM神经网络模型的振动性[J]. 数学物理学报, 2011, 31(6): 1490-1501. |
| [13] | 张若军, 王林山. 具有分布时滞的细胞神经网络的概周期解[J]. 数学物理学报, 2011, 31(2): 422-429. |
| [14] | 邹劭芬, 王耀南, 黄立宏. 三元环状神经网络的稳定性[J]. 数学物理学报, 2010, 30(6): 1654-1665. |
| [15] | 俞国华. Lp空间中神经网络逼近的几何速度[J]. 数学物理学报, 2010, 30(3): 848-856. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 117
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 106
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|