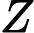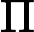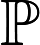数学物理学报 ›› 2022, Vol. 42 ›› Issue (3): 957-974.doi: 10.1007/s10473-022-0309-3
CENTRAL LIMIT THEOREM AND CONVERGENCE RATES FOR A SUPERCRITICAL BRANCHING PROCESS WITH IMMIGRATION IN A RANDOM ENVIRONMENT
李应求1, 黄绪兰2, 彭朝晖2
- 1. Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering, School of Mathematics and Statistics, Changsha University of Science and Technology, Changsha, 410004, China;
2. School of Mathematics and Statistics, Changsha University of Science and Technology, Changsha, 410004, China
CENTRAL LIMIT THEOREM AND CONVERGENCE RATES FOR A SUPERCRITICAL BRANCHING PROCESS WITH IMMIGRATION IN A RANDOM ENVIRONMENT
Yingqiu LI1, Xulan HUANG2, Zhaohui PENG2
- 1. Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering, School of Mathematics and Statistics, Changsha University of Science and Technology, Changsha, 410004, China;
2. School of Mathematics and Statistics, Changsha University of Science and Technology, Changsha, 410004, China
摘要: We are interested in the convergence rates of the submartingale to its limit where is the usually used norming sequence and is a supercritical branching process with immigration in a stationary and ergodic environment . Under suitable conditions, we establish the following central limit theorems and results about the rates of convergence in probability or in law: (i) with suitable normalization converges to the normal law , and similar results also hold for for each fixed (ii) for a branching process with immigration in a finite state random environment, if has a finite exponential moment, then so does and the decay rate of is supergeometric; (iii) there are normalizing constants (that we calculate explicitly) such that converges in law to a mixture of the Gaussian law.
中图分类号:
- 60J80