[1] Acerbi E, Mingione G. Regularity results for stationary electro-rheological fluids. Arch Ration Mech Anal, 2002, 164(3): 213-259
[2] Acerbi E, Mingione G. Gradient estimates for a class of parabolic systems. Duke Math J, 2007, 136: 285-320
[3] Adams D R. A note on Riesz potentials. Duke Math J, 1975, 42: 765-778
[4] Baroni P. Lorentz estimates for degenerate and singular evolutionary systems. J Differ Equ, 2013, 255: 2927-2951
[5] Byun S S, Ryu S. Global weighted estimates for the gradient of solutions to nonlinear elliptic equations. Ann Inst H Poincaré AN, 2013, 30: 291-313
[6] Byun S S, Wang L.   -estimates for general nonlinear elliptic equations. Indiana Univ Math J, 2007, 56(6): 3193-3221 -estimates for general nonlinear elliptic equations. Indiana Univ Math J, 2007, 56(6): 3193-3221
[7] Byun S S, Yao F, Zhou S. Gradient estimates in Orlicz space for nonlinear elliptic equations. J Funct Anal, 2008, 255(8): 1851-1873
[8] Caffarelli L A, Peral I. On     estimates for elliptic equations in divergence form. Commun Pure Appl Math, 1998, 51(1): 1-21 estimates for elliptic equations in divergence form. Commun Pure Appl Math, 1998, 51(1): 1-21
[9] DiBenedetto E, Manfredi J. On the higher integrability of the gradient of weak solutions of certain degenerate elliptic systems. Amer J Math, 1993, 115(5): 1107-1134
[10] Diening L.Theoretical and numerical results for electro-rheological fluids [D]. Breisgau: Universität Freiburg, 2002
[11] Eleuteri M, Harjulehto P, Lukkari T. Global regularity and stability of solutions to elliptic equations with nonstandard growth. Complex Var Elliptic Equ, 2011, 56: 599-622
[12] Esposito L, Mingione G, Trombetti C. On the Lipschitz regularity for certain elliptic problems. Forum Math, 2006, 18(2): 263-292
[13] Giova R. Regularity results for non-autonomous functionals with    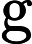  -growth and Orlicz Sobolev coefficients. NoDEA Nonlinear Differential Equations Appl, 2016, 23(6): 1-18 -growth and Orlicz Sobolev coefficients. NoDEA Nonlinear Differential Equations Appl, 2016, 23(6): 1-18
[14] Giusti E.Direct Methods in the Calculus of Variations. River Edge, NJ: World Scientic Publishing, 2003
[15] Glowinski R, Rappaz J. Approximation of a nonlinear elliptic problem arising in a non-Newtonian fluid model in glaciology. M2AN Math Model Numer Anal, 2003, 37(1): 175-186
[16] Grafakos L.Classical and Modern Fourier Analysis. Upper Saddle River, NJ: Pearson/Prentice Hall, 2004
[17] Iwaniec T. Projections onto gradient fields and   -estimates for degenerated elliptic operators. Stud Math, 1983, 75(3): 293-312 -estimates for degenerated elliptic operators. Stud Math, 1983, 75(3): 293-312
[18] Iwaniec T.The Gehring Lemma//Duren P, Heinonen J, Osgood B, Palka B. Quasiconformal Mappings and Analysis. New York: Springer, 1998
[19] Kinnunen J. The Hardy-Littlewood maximal function of a Sobolev function. Israel J Math, 1997, 100: 117-124
[20] Kinnunen J, Saksman E. Regularity of the fractional maximal function. Bull Lond Math Soc, 2003, 35: 529-535
[21] Kinnunen J, Zhou S. A local estimate for nonlinear equations with discontinuous coefficients. Commun Partial Differ Equ, 1999, 24(11/12): 2043-2068
[22] Kinnunen J, Zhou S. A boundary estimate for nonlinear equations with discontinuous coefficients. Differ Integral Equ, 2001, 14(4): 475-492
[23] Krylov N V, Safonov M V. A property of the solutions of parabolic equations with measurable coefficients. Izv Akad Nauk SSSR Ser Mat, 1980, 44(1): 161-175
[24] Kuusi T, Mingione G. Guide to nonlinear potential estimates. Bull Math Sci, 2014, 4(1): 1-82
[25] Lee M, Ok J. Nonlinear Calderón-Zygmund theory involving dual data. Rev Mat Iberoamericana, 2019, 35(4): 10530-11078
[26] Mengesha T, Phuc N C. Global estimates for quasilinear elliptic equations on Reifenberg flat domains. Arch Ration Mech Anal, 2012, 203(1): 189-216
[27] Mingione G. Gradient estimates below the duality exponent. Math Ann, 2010, 346: 571-627
[28] Muckenhoupt B, Wheeden R L. Weighted norm inequalities for fractional integrals. Trans Amer Math Soc, 1974, 192: 261-274
[29] Nguyen T N, Tran M P. Lorentz improving estimates for the  -Laplace equations with mixed data. Nonlinear Anal, 2020, 200: 111960 -Laplace equations with mixed data. Nonlinear Anal, 2020, 200: 111960
[30] Nguyen T N, Tran M P. Level-set inequalities on fractional maximal distribution functions and applications to regularity theory. J Funct Anal, 2021, 280(1): 108797
[31] Nguyen T N, Tran M P, Doan C K, Vo V N. A gradient estimate related fractional maximal operators for a  -Laplace problem in Morrey spaces. Taiwanese J Math, 2021, 25(4): 809-829 -Laplace problem in Morrey spaces. Taiwanese J Math, 2021, 25(4): 809-829
[32] Nguyen T N, Tran M P, Tran N T. Regularity estimates for stationary Stokes problem in some generalized function spaces. Z Angew Math Phys, 2023, 74(1): Art 13
[33] Pélissier M C, Reynaud M L. Étude d'un modéle mathematique d'écoulement de glacier. C R Acad Sci Paris Ser I Math, 1974, 279: 531-534
[34] Rajagopal K R, Ružička M. Mathematical modelling of electro-rheological fluids. Cont Mech Therm, 2001, 13: 59-78
[35] Reifenberg E. Solution of the Plateau problem for  -dimensional surfaces of varying topological type. Acta Math, 1960, 104: 1-92 -dimensional surfaces of varying topological type. Acta Math, 1960, 104: 1-92
[36] Showalter R E, Walkington N J. Diffusion of fluid in a fissured medium with microstructure. SIAM J Math Anal, 1991, 22: 1702-1722
[37] Tran M P, Nguyen T N. Existence of a renormalized solution to the quasilinear Riccati-type equation in Lorentz spaces. C R Acad Sci Paris Ser I, 2019, 357(1): 59-65
[38] Tran M P, Nguyen T N. Lorentz-Morrey global bounds for singular quasilinear elliptic equations with measure data. Commun Contemp Math, 2020, 22(5): 1950033
[39] Tran M P, Nguyen T N. New gradient estimates for solutions to quasilinear divergence form elliptic equations with general Dirichlet boundary data. J Differ Equ, 2020, 268(4): 1427-1462
[40] Tran M P, Nguyen T N. Global Lorentz estimates for non-uniformly nonlinear elliptic equations via fractional maximal operator. J Math Anal Appl, 2021, 501(1): 124084
[41] Tran M P, Nguyen T N. Global gradient estimates for very singular quasilinear elliptic equations with non-divergence data. Nonlinear Anal, 2022, 214: 112613
[42] Tran M P, Nguyen T N. Gradient estimates via Riesz potentials and fractional maximal operators for quasilinear elliptic equations with applications. Nonlinear Anal: Real World Appl, 2023, 69: 103750 |