时滞现象在生物神经网络与人工神经网络中广泛存在, 它是导致系统振动与不稳定性的关键因素之一. 因此, 针对具有时滞特性的神经网络进行深入研究一直是该领域的热点话题^[1,2]. 比例时滞是一种无界时滞, 文献 [3] 基于 QoS 路由决策需要比例时滞保证且可由神经网络实现提出了比例时滞神经网络, 此后比例时滞神经网络的动力学得到了国内外学者的广泛研究, 如稳定性^[4,5,6,7]、无源性^[8]、周期性^[9]等. 同步性作为稳定性的延申, 由于其在保密通信^[10]、图像保护^[11]等领域的应用而得到了广泛研究, 如文献 [12] 利用比较原理和时间尺度理论探讨了一类时标型非自治比例时滞神经网络的同步问题.文献 [13] 通过设计量化控制技术, 利用 Wirdinger 不等式及构造 Lyapunov -Krasovskii 泛函分析了比例时滞耦合反应扩散神经网络的渐近同步. 文献 [14] 通过构造 Lyapunov 泛函, 设计合适的控制输入研究了比例时滞递归神经网络的指数同步和多项式同步, 并揭示了指数同步和多项式同步之间的关系.

自从 Babcock 和 Wheeler 在文献 [15] 中提出了惯性神经网络以来, 其动力学研究取得了许多成果^[16,17]. 时滞惯性神经网络的同步与混沌控制是近几十年来的研究热点之一^[18], 比例时滞惯性神经网络的同步研究也取得一些成果, 如文献 [19] 采用非降阶方法和 Lyapunov 稳定性理论探究了比例时滞的脉冲复值惯性神经网络的全局指数镇定和指数滞后同步. 文献 [20] 利用微分包含理论和降阶变换、设计反馈控制器与自适应控制器以及构造 Lyapunov 泛函探讨了比例时滞惯性忆阻 Cohen-Grossberg 神经网络的全局渐近同步. 文献 [21] 设计反馈控制器、采用降阶方法和构造范数形式的比例时滞微分不等式研究了比例时滞惯性神经网络的全局多项式同步, 但相比其他有界时变时滞惯性神经网络的同步控制研究, 该领域仍有巨大的研究空间.

除了时滞影响, 环境噪声也是系统运行过程中不可避免的因素, 在神经网络中考虑噪声的影响能更好的刻画网络的实际状态, 因此, 随机神经网络的动力学研究具有重要的现实意义.近年来, 对于有界时变时滞的随机神经网络动力学的研究成果较为丰富^[22,23,24].然而, 关于比例时滞随机神经网络的动力学研究仍非常有限^[25,26], 文献[25] 利用 Lyapunov -Krasovskii 泛函、随机分析理论和 Itô 公式研究了多比例时滞随机递归神经网络状态稳定性的均方指数输入状态稳定性. 文献 [26] 设计了一种延迟反馈控制器和采用 Lyapunov 方法分析了比例时滞随机复值忆阻模糊细胞神经网络的固定时间同步. 目前, 关于比例时滞惯性随机神经网络的均方指数同步研究鲜有报道.

基于这些启发, 本文将考虑一类比例时滞惯性随机神经网络均方指数同控制问题, 并进一步将所研究的均方指数同步应用于图像加密. 本文的创新性及主要贡献总结如下

(1) 与以往有界时滞神经网络的同步研究^[1,2,22,23]相比,本文研究对象是一类无界时滞神经网络, 由于比例时滞的无界性使得其在同步研究过程中处理起来比较困难.关于比例时滞的处理方法, 以前的文献 [3,14] 是通过利用非线性变换将比例时滞神经网络转换成常时滞神经网络, 再利用常时滞神经网络的同步控制方法进行研究, 其缺点是过程繁琐且结果具有较强的保守性.本文没有使用上述常规的比例时滞的处理方法, 而是在比例时滞的状态下直接进行神经网络的同步分析.

(2) 对比以前的研究结果, 如文献[12,13,14,19,20], 这些结果均是通过构造 Lyapunov 泛函的方法进行同步控制研究的.众所周知, Lyapunov 泛函的构造没有固定的方法, 构造新颖的恰当的 Lyapunov 泛函非常困难.本文除了使用构造新颖的 Lyapunov 方法以外, 还利用微积分的性质直接进行所研究系统的均方指数同步分析, 该方法更加直观和简洁, 该方法也可推广到其他比例时滞神经的周期性和耗散性的研究.

(3) 与以往的随机神经网络同步研究^[22,23,24]相比, 本文考虑了惯性项的影响, 这一二阶导数项的存在增加同步控制研究的难度, 同时使模型更为复杂, 但有利于刻画神经网络的实际状态.并将所得均方指数同步控制通过设计加密算法成功地应用于图像的加密领域.

符号说明: $\mathbb{R}$、$\mathbb{R_{+}}$、$\mathbb{R}^{n}$ 分别表示实数集、正实数集、欧氏空间. $E(\cdot)$ 表示数学期望. 对于 $x=(x_{1},x_{2},\cdots,x_{n})^{T}\in \mathbb{R}^{n}$, $\|x\|=\sqrt{\sum_{i=1}^{n}x_{i}^{2}}$. $C=C([\bar{q}t_{0},t_{0}],\mathbb{R})$ 表由 $[\bar{q}t_{0},t_{0}]$ 到 $\mathbb{R}$ 的所有连续函数的集合. $\hat{n}=\{1,2,\cdots,n\}$. $E$ 表示相应维数的单位矩阵.

考虑如下一类比例时滞惯性随机神经网络

其中 $x_{i}(t)$ 表示系统状态, $\beta_{i}>0, \alpha_{i}>0, a_{i j}, b_{i j}$ 表示反馈连接权值, $q_{i j}\in(0,1)$ 为比例时滞因子, $q_{ij}t=t-(1-q_{ij})t$, $(1-q_{ij})t$ 为时滞传输函数, $(1-q_{ij})t\rightarrow+\infty$ (当 $t\rightarrow+\infty$ 时), $f_{j}(\cdot)$ 为系统输出函数, $I_{i}(t)$ 表示偏置性输入, $c_{i j} g_{j}\left(x_{j}(t)\right) \mathrm{d}B_{i}(t)$ 表示随机扰动项, 并且 $B(t)=\left(B_{1}(t), B_{2}(t), \cdots, B_{n}(t)\right)^{T}$ 为定义在完备概率空间 $(\Omega, \mathcal{F}, P)$ 上具有自然滤波 $\left\{\mathcal{F}_{t}\right\}_{t \geq 0}$ 上的 $n$ 维布朗运动. $\varphi_{i}(s)$, $\psi_{i}(s)\in C$ 表示初值条件.

将系统 (2.1) 作为驱动系统, 取响应系统如下

其中 $u(t)=\left(u_{1}(t), u_{2}(t), \cdots, u_{n}(t)\right)^{T}$ 表示控制器, $\bar{\varphi}_{i}(s)$, $\bar{\psi}_{i}(s)\in C$ 表示初值条件.

作系统 (2.1) 和 (2.2) 的误差系统, 令 $e_{i}(t)=y_{i}(t)-x_{i}(t)$, 得

其中 $\bar{f}_{j}(e_{j}(t))=f_{j}(y_{j}(t))-f_{j}(x_{j}(t))$, $\bar{f}_{j}(e_{j}(q_{ij}t))=f_{j}(y_{j}(q_{ij}t))-f_{j}(x_{j}(q_{ij}t))$, $\bar{g}_{j}(e_{j}(t))=g_{j}(y_{j}(t))-g_{j}(x_{j}(t))$, $\hat{\varphi}_{i}(s)=\bar{\varphi}_{i}(s)-\varphi_{i}(s)$, $\hat{\psi}_{i}(s)=\bar{\psi}_{i}(s)-\psi_{i}(s)$.

其中 $\gamma_{i}=\alpha_{i} \eta_{i}-\beta_{i}-\eta_{i}^{2}$, $\zeta_{i}=\eta_{i}-\alpha_{i}$.

本文对 $f_{j}(\cdot)$ 和 $g_{j}(\cdot)$ 作以下假设

(H$_{1})$ 存在常数 $L_{j}>0$, 使得

(H$_{2})$ 存在常数 $M_{j}>0$, 使得

在文献 [27] 中, 对于系统

其中 $h \in\left[\mathbb{R}_{+} \times \mathbb{R}^{n}, \mathbb{R}^{n}\right], m \in\left[\mathbb{R}_{+} \times \mathbb{R}^{n}, \mathbb{R}^{n\times n}\right]$ 是 Borel 可测函数, 定义微分算子

对于 $V(t, z) \in C^{1,2}\left[\mathbb{R}_{+} \times S_{h}, \mathbb{R}_{+}\right]$, 有

这里$S_{d}=\{z \mid\|z\| \leq d\} \in \mathbb{R}^{n}, \quad \frac{\partial V}{\partial z}=\left(\frac{\partial V}{\partial z_{1}}, \frac{\partial V}{\partial z_{2}}, \cdots \frac{\partial V}{\partial z_{n}}\right)^{T}, \quad \frac{\partial^{2} V}{\partial z \partial z}=\left(\frac{\partial^{2} V}{\partial z_{i} \partial z_{j}}\right)_{n \times n}.$

若$z(t) \in S_{h}$, 利用 Itô 公式, 则

引理 2.1^[27] 设 $T>0, z(t)$ 为区间 $[T]$ 上的 Borel 非负有界函数, 若

则 $z(t)\leq \theta \mathrm{e}^{\mu t}$, 其中 $\theta$ 和 $\mu$ 为常数, $t\in[T]$.

定义 2.1 在某一控制器 $u(t)$ 下, 若存在常数 $\mu>0, \theta>0$ 使得

则称系统 (2.1) 和 (2.2) 能达到均方指数同步.

设计如下控制器

定理3.1 假设 (H$_{1})$-(H$_{2})$ 成立, 在控制器 (3.1) 下, 若

则系统 (2.1) 和 (2.2) 能达到均方指数同步.

证 令 $\epsilon(t)=\left(e_{1}(t), e_{2}(t), \cdots, e_{n}(t), \omega_{1}(t), \omega_{2}(t), \cdots, \omega_{n}(t)\right)^{T}$, 考虑 Lyapunov 泛函

且 $V_{t}(t, \epsilon(t))=\sum_{i=1}^{n} \sum_{j=1}^{n}\left|b_{i j}\right| L_{j}\left(q_{i j}^{-1} e_{j}^{2}(t)-e_{j}^{2}\left(q_{i j} t\right)\right)$, $V_{\epsilon(t)}(t, \epsilon(t))=2 \epsilon(t)$, $V_{\epsilon(t) \epsilon(t)}(t, \epsilon(t))\\=2 E_{2 n \times 2 n}.$

由 (2.4), (2.5) 和 (3.2) 式, 得

由 (H$_{1})$-(H$_{2})$, 以及均值不等式, 得

其中 $\mu=\min _{ i\in \hat{n}}\left\{p_{i}, \rho_{i}\right\}>0$. 于是, 得

另一方面, 由 (2.6) 式, 知

这里 $C=(c_{ij})_{n\times n}$, $\bar{g}(e(t))=(\bar{g}_{1}(e_{1}(t)),\cdots,\bar{g}_{n}(e_{n}(t)))^{T}$. 对 (3.4) 式从 $t_{0}$ 到 $t$ 积分, 可得

由 (3.2)-(3.5) 式, 得

对 (3.6) 式两边取数学期望, 得

其中 $\theta=\sum_{i=1}^{n} \mathrm{E}\big[e_{i}^{2}(t_{0})+\omega_{i}^{2}(t_{0})+\sum_{j=1}^{n}\left|b_{i j}|q_{ij}^{-1}\right| L_{j} \int_{q_{i j}t_{0}}^{t_{0}}(\hat{\varphi}_{i}(s))^{2} \mathrm{d}s\big]>0$.

由引理 2.1, 由 (3.7) 式, 得

因此, 根据定义 2.1 可知系统 (2.1) 和 (2.2) 在控制器(3.1) 作用下均方指数同步.

注 3.1 本文构造正定的 Lyapunov 泛函 (3.2) 的新颖性有两点: 1) 积分项前面乘上 $q_{ij}^{-1}$, 目的是为了约去 Lyapunov 泛函求导后积分下限求导后出现的 $q_{ij}$; 2) 积分项的作用是 Lyapunov 泛函求导后, 在均值不等式的帮助下, 消去含有比例时滞的项.

定理 3.1 是通过构造 Lyapunov 泛函, 结合已知条件等进行系统 (1) 和 (2) 的均方指数同步探究的.接下来, 本文不构造 Lyapunov 泛函, 而是直接通过微积分的相应性质进行均方指数同步分析.

定理 3.2 假设 (H$_{1})$ 成立, 在控制器 (3.1) 下, 若

则系统 (2.1) 和 (2.2) 能达到均方指数同步.

证 由 (2.4) 式, 得

对上式两边从 $t_{0}$ 到 $t$ 积分, 可得

再由均值不等式, 得

由于

将 (3.10) 式代入 (3.9) 式, 可得

其中 $\mu^{\ast}=\min _{ i \in \hat{n}}\left\{p_{i}^{\ast}, \rho_{i}^{\ast}\right\}>0$. 在 (3.11) 式两边取数学期望, 得

其中 $\theta^{\ast}=\sum\limits_{i=1}^{n}\{\mathrm{E}\left(e_{i}^{2}(t_{0})+\omega_{i}^{2}(t_{0})\right)+2 \sum\limits_{j=1}^{n}L_{j}|b_{ij}|q_{ij}^{-1}\int_{q_{ij}t_{0}}^{t_{0}}\hat{\varphi}_{i}^{2}(s)\mathrm{d} s\}>0$.

由引理 1 和 (3.12), 可得

即系统 (2.1) 和 (2.2) 在控制器 (3.1) 作用下均方指数同步.

注 3.2 定理 3.1 和 3.2 都依赖于比例时滞因子, 但定理 3.2 不要求 $g_{j}$ 满足 $\rm{Lipschitz}$ 条件.因此, 可根据具体情况, 选择合适的定理作为系统均方指数同步的判定法则.

注 3.3 在系统 (2.1) 和 (2.2) 中, 若不考虑随机项, 本文所得结果仍然成立. 当 $q_{i j}=q$, $q \in(0,1)$, $i, j\in\hat{n}$ 时, 定理 3.1-3.2 仍成立. 当 $q_{i j}=1$ 时, 系统 (2.1) 和 (2.2) 就成为无时滞惯性随机神经网络, 定理 3.1-3.2 仍成立.

例 4.1 在系统 (2.1) 和 (2.2) 中, 选取系统参数及控制器参数如下: $\alpha=\operatorname{diag}(0.01,0.01)$, $\beta=\operatorname{diag}(0.005,0.002)$, 且

此时, 函数 $f_{j}(\cdot), g_{j}(\cdot)$ 符合假设 (H$_{1})$ 和 (H$_{2})$, 且 $L_{j}=M_{j}=1, j=1,2$.

情况 1 存在比例时滞情况下, 取 $q_{11}=0.5, q_{12}=0.8, q_{21}=0.7, q_{22}=0.9$, 计算, 得

满足定理 3.1, 因此, 系统 (2.1) 和 (2.2) 在控制器 (3.1) 的作用下能达到均方指数同步.

取初值 $\left[x_{1}(0), \dot{x}_{1}(0), y_{1}(0), \dot{y}_{1}(0)\right]^{\mathrm{T}}\!=\![2,0.3,0.7,0.5]^{\mathrm{T}}$, $\left[x_{2}(0), \dot{x}_{2}(0), y_{2}(0)\right.$, $\left.\dot{y}_{2}(0)\right]^{\mathrm{T}}\!=\![1,0.6,$$0.4,0.7]^{\mathrm{T}}$, 驱动系统 (2.1) 与不受控的响应系统 (2.2) 均为混沌系统, 相图如图 1(a) 和 (b) 所示, 相应的状态轨迹如图 2(a) 和 (b) 所示. 而在控制器 (3.1) 作用下, 系统 (2.1) 和 (2.2) 的相图和状态轨迹除初始部分以外是一致的, 如图 1(c) 和图 2(c) 所示. 系统 (2.1) 与 (2.2) 在控制器 (3.1) 作用下均方指数同步, 如图 3(a) 所示.

情况 2 无比例时滞情况下, 此时 $q_{11}= q_{12}= q_{21}= q_{22}=1$, 计算, 得

满足注 3.3, 因此此时无时滞系统 (2.1) 和 (2.2) 在控制器 (3.1) 的作用下能达到均方指数同步, 如图 3(b) 所示.

对比图 3(a) 和图 3(b), 我们发现该例中比例时滞的确对驱动和响应系统的均方指数同步产生了影响, 使得同步时间长于无时滞的情况.

例 4.2 以图像的加密和解密为例给出本文所研究的指数同步在保密通信中的应用.

利用例 4.1 中系统 (2.1) 和 (2.2) 的指数同步结果进行图像的加密和解密, 并通过直方图、信息熵、同步误差和散点图等给出其相应的安全性分析.

选取图像 $A$, 如图 4(a) 所示, 通过同步后的驱动-响应系统 (2.1) 和 (2.2) 对图像 $A$ 进行加密和解密, 过程如下

(1) 像素读取, 读取要进行加密的彩色图像 $A$, 按 $R${(红)}, $G$ {(绿)}, $B$ {(蓝)}三通道将原图像素值以矩阵形式保存为$R_{a}$、$G_{a}$ 和 $B_{a}$.

(2) 置换加密, 生成两组伪随机序列 $D_{1}$ 和 $D_{2}$. 通过 $D_{1}$ 分别对矩阵 $R_{a}$、$G_{a}$ 和 $B_{a}$ 进行置换加密, 再将三通道矩阵合并可得到置换加密后的图像.

(3) 图像加密, 基于例 4.1 给出的模型参数和初值, 可以得到驱动系统序列 $(x_{1},x_{2})$, 并对序列进行截取, 通过 $D_{1}$ 对序列进行置换得到序列 $(Sen_{1},Sen_{2})$, 由 $(Sen_{1},Sen_{2})$ 生成与原图对应的矩阵形式秘钥

将矩阵 $r$, $g$, $b$ 合并得到秘钥, 将图像 $A$ 与秘钥做 $\mathrm{XOR}$ 运算得到加密后的图像 $A^{\prime}$.

(4) 图像解密, 由响应系统可得序列 $(y_{1},y_{2})$, 通过 $D_{1}$ 对序列进行置换得到序列 $(Sen_{3}$, $Sen_{4})$, 按照与加密过程相同的规则生成解密密钥, 对图像 $A^{\prime}$ 进行 $\mathrm{XOR}$ 运算, 再进行置换还原得到原始图像 $A$, 完成解密.

实验结果如图 4(a)-(c) 所示. 图 4(b) 是使用驱动系统序列导出的加密图像, 其掩盖了原始图像中包含的信息. 另一方面, 图 4(c) 是利用响应系统序列重建的解密图像, 从该图可观察到加密图像已完全恢复. 接下来, 将进一步分析所提出的图像加密算法的安全性.

直方图是像素值分布的关键指标, 有效加密系统旨在使加密图像的直方图均匀. 本文分析了 $R_{a}$、$G_{a}$ 和 $B_{a}$ 组合直方图 (如图4(d)-(f)). 图 4(d) 和 (e) 展示了加密后图像的均匀直方图特性, 有效应对统计分析型攻击, 使攻击者难以通过统计手段解析原始图像. 图 4(d) 和 (f) 的相似性表明了解密算法的保真度, 保留了原始像素分布, 证明了本文图像加密解密方法的有效性和准确性.

图像信息熵是衡量图像随机性或不确定性水平的关键指标, 定义为

其中 $p(s_{i})$ 是像素灰度值 $s_{i}$ 的概率. 图像越混沌或像素分布越均匀, 信息熵 $H(s)$ 越高. 理想均匀分布下, 8位灰度图像的信息熵为8. 图4(a)-(c) 的信息熵如表 1 所示, 加密图像信息熵达 $7.99111$, 表明其具有良好的混沌性和较高安全性.

本文通过分析系统在受到不同程度的同步误差时的解密性能, 来检查加密密钥的敏感性. 图5(a)-(c) 出示了图像的解密效果随着同步误差的增加而降低, 表明我们的图像加密算法具有较高的灵敏度. 若将驱动响应系统的混沌序列应用于图像保护, 本文应该努力使同步误差尽可能小 $[ \|e(t)\|\leq 10^{-5} 秒]$.

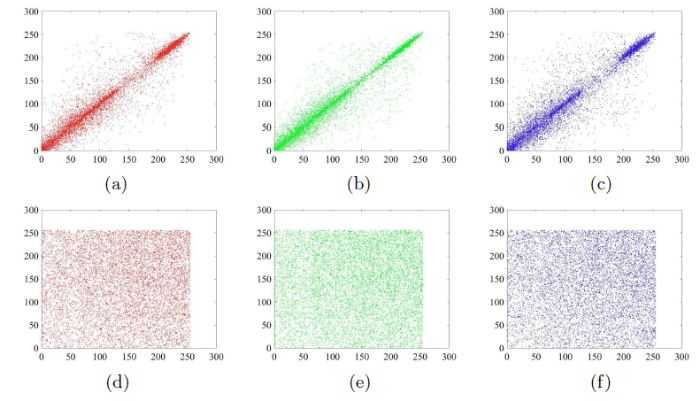
在相邻像素之间, 为了防止统计攻击, 必须减少信息相关性. 表2详细说明了图像中三个不同方向上相邻像素点的相关性, 实验结果表明, 水平、垂直和对角线加密的 $R$、$G$、$B$ 图像分量中相邻像素之间的相关性趋于零. 这意味着像素在这三个方向上几乎没有相关性, 证明了加密算法对统计分析的鲁棒性. 图6(a)-(f) 通过显示原始图像和加密图像中相邻像素的散点图进一步说明了这一点. 原始图像的散点图, 如图 6(a)-(c) 所示, 显示了相邻像素之间强烈的正线性关系. 相比之下, 加密图像的散点图, 如图 6(d)-(f) 显示了三个方向上相邻像素的不相关性, 这表明加密图像具有良好的隐私性.

注 4.1 在例 4.1 中, 本文通过数值算例和仿真验证了所得的比例时滞随机神经网络的均方指数同步准则的有效性. 文献 [22,23,24] 研究的有界时变时滞的情况, 并且没有考虑惯性项的作用, 因此他们的结果均不能应用于本文的例 4.1. 并且这些随机神经网络同步研究, 只是在理论层面上进行的, 并没有进行同步控制实际应用的探究.本文不但获得了所研究系统的均方指数同步准则及收敛速率, 还通过例 4.2 将所得均方指数同步控制通过设计加密算法等成功地应用于图像加密领域.不但验证了同步控制和加密算法的有效性, 还为比例时滞随机神经网络可进行实际应用探索出了一条新路径.

本文探究了一类比例时滞惯性随机神经网络的均方指数同步及其在图像加密和解密中的应用. 通过设计反馈控制器, 运用 Itô 公式, 构建 Lyapunov 泛函和利用微积分的性质, 得到了所研究系统均方指数同步的时滞所依赖的代数形式的充分条件, 条件简单, 易于验证. 通过数值例题及仿真验证了所得到理论结果是正确的. 同时, 将例 4.1 中驱动-响应系统的均方指数同步应用于图像的加密和解密, 并从直方图、信息熵、误差比较和散点图的实验结果表明本文设计的同步方案和加密算法对保密通信是合理有效的. 本文的研究方法也适用于比例时滞神经网络的周期性和无源性的研究, 图像加密和解密的方法也可应用于其他神经网络在保密通信中应用.