1 引言
给定一个非空集合 X, f:X→X 是一个自映射, 记
本文研究了可分逐段严格单调的 Markov 映射的迭代, 即存在特殊的不动点将映射划分为在多个子区间上逐段严格单调的 Markov 自映射, 将整体的迭代简化为对局部的迭代, 并分别给出子区间上映射的迭代与具体表达式.
2 准备工作
给定映射 f:I:=[a,b]→I, 如果 f 在 x0∈I 的小邻域内严格单调, 则称 x0 为 f 的 "单调点", 否则为 f 的 "非单调点" (参见文献 [18]). 令集合 PM(I,I) 表示定义在区间 I 上的所有具有有限多非单调点的连续自映射, S(f) 为 f∈PM(I,I) 的所有非单调点集合. 下面给出可分映射与可拼接映射的定义.
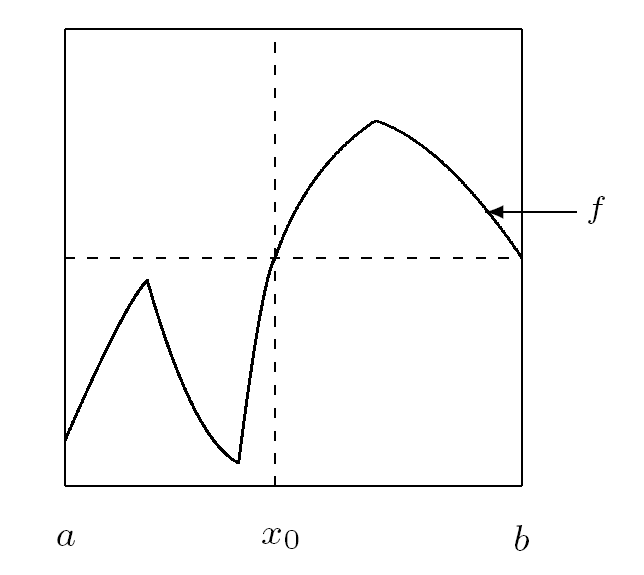
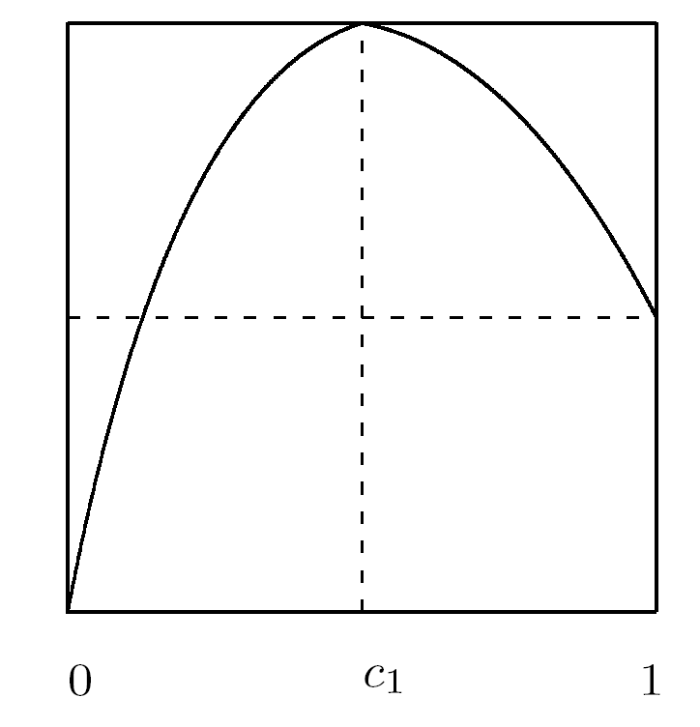
定义2.1 令 f∈PM(I,I), 若存在不动点 x0 使得
其中 f1(I1)⊂I1, f2(I2)⊂I2, 则称 f 为可分映射, x0 为 f 的可分不动点 (如图 2.1). 令集合 F(f) 表示 f 的所有可分不动点.
图 2.1
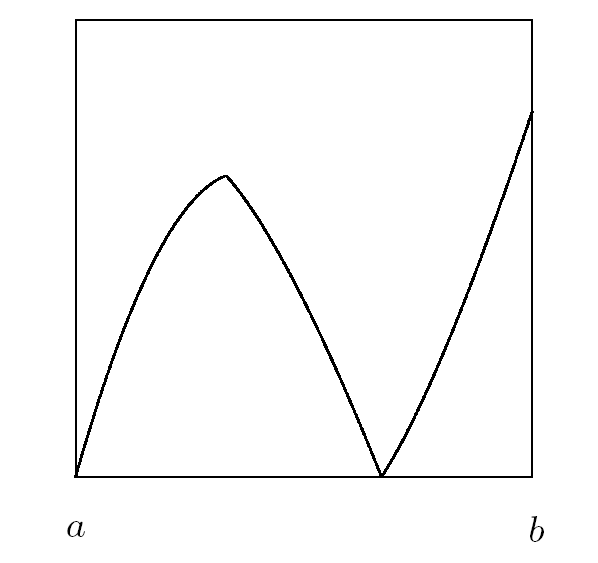
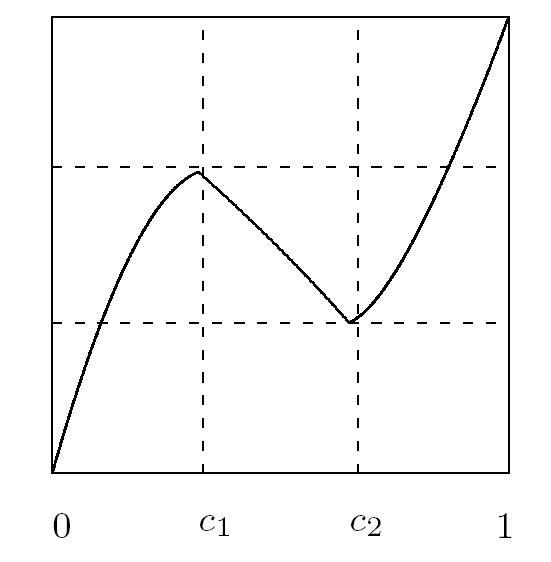
定义2.2 令 f∈PM(I,I), I=[a,b], 若 f(a)=a 或 f(b)=b, 且区间 I 内部无可分不动点, 则称 f 为可拼接映射 (如图 2.2).
图 2.2
由定义 2.1 和定义 2.2 可知一个可分映射可以被可分不动点划分为一些可拼接映射, 从而可分映射的 n 次迭代可以转化为这些可拼接自映射的 n 次迭代. 特别地, 我们只考虑 f 可分不动点有限的情形, 否则一定存在区间 [a′,b′]⊂I 使得 f 为恒等映射, 其任意次迭代仍为恒等映射, 从而
那么显然有 I=⋃mi=0Ii:=⋃mi=0[xi,xi+1], 对 f:I→I 有
接下来我们将给出可分映射与 Markov 映射之间的关系.
定义2.3 (参见文献 [13]) 设 f∈PM(I,I), S(f):={a1,a2,⋯,am} 且 a0=a,am+1=b, 若 E(f)={fn(ai)|n∈Z+,i=0,1,⋯,m+1} 是个有限集, 则称 f 为 Markov 自映射.
接下来我们将给出可分映射与 Markov 映射之间的关系.
定理2.1 令 f∈PM(I,I) 且定义在 (2.1) 式中, 则 f 为 Markov 映射当且仅当对任意的 i=0,1,⋯,m 都有 fi 为 Markov 映射.
证 必要性. 由假设 f 为 Markov 映射和定义 2.3 知 E(f) 为有限集, 且对任意的 i∈{0,1,⋯,m} 都有 xi∈F(f), 即 {fn(xi)|n∈Z+}={xi}, 故 E(fi)⊂E(f)∪{xi,xi+1} 为有限集, 这意味着 fi:[xi,xi+1]→[xi,xi+1] 为 Markov 映射.
充分性. 由假设对任意的 i∈{0,1,⋯,m} 都有 fi 为 Markov 映射, 可知 E(fi) 为有限集. 从而 E(f)⊂⋃mi=0E(fi) 为有限集. 即 f 为 Markov 映射.
现令 S∗(f):=S(f)∪{a,b}, 本文我们研究 f(S∗(f))⊂S∗(f) 的可分映射的迭代, 显然 f 也是 Markov 映射. 由定理 2.1 知可分 Markov 映射是由有限多个可拼接的 Markov 自映射构成, 而自映射的迭代仍在其定义的区间上, 故接下来我们只讨论这类自映射的迭代. 现令 g∈PM(I,I) 为可拼接的 Markov 自映射, 其非单调点集
其中 N(g) 表示其非单调点的个数, 并不失一般性令 I=[a,b]=[0,1]. 那么显然 g 由一系列分段单调映射组成, 即
根据区间端点的性质, 该类映射可以分为以下两类
A :={g∈PM(I,I)|g为 Markov 映射,g(0)=0,g(1)≠1 或 g(0)≠0,g(1)=1},
B :={g∈PM(I,I)|g为 Markov 映射,g(0)=0 且 g(1)=1}.
3 g∈A 的情形
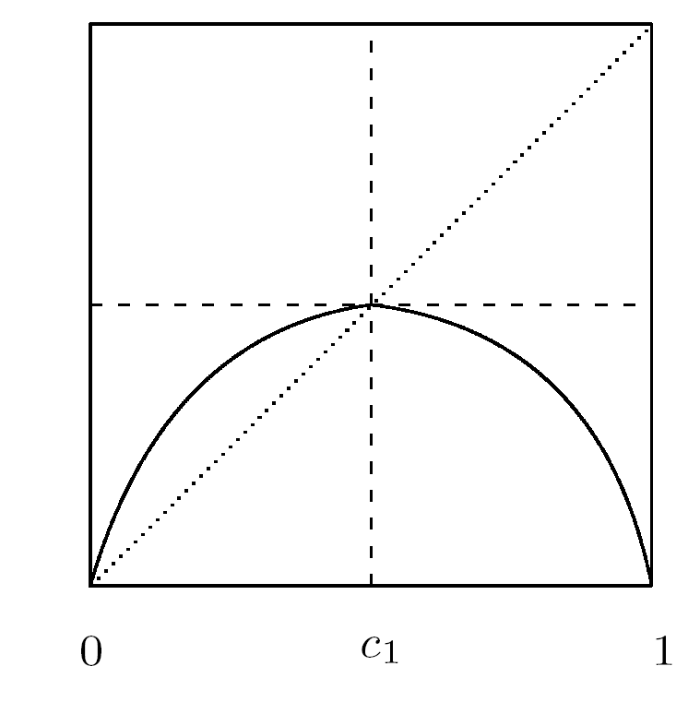
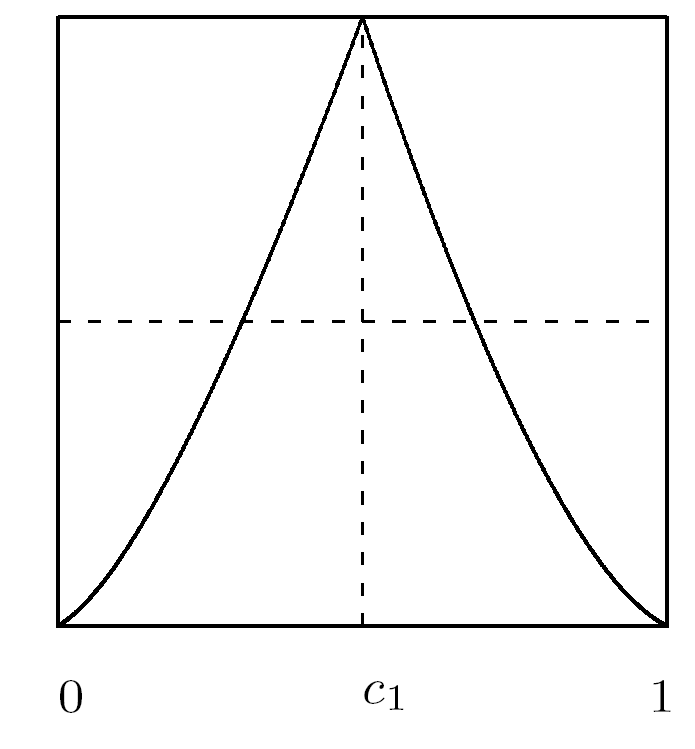
由于 g∈A 且 g(0)=0 的情形与 g∈A 且 g(1)=1 的情形可以通过一个反向同胚相互共轭, 因此我们首先考虑前一种情形并满足 N(g)=1. 令
图3.1
图3.2
图3.3
下面我们将分别给出这 3 类映射的正整数 n 次迭代的具体表达式.
定理3.1 若 g∈A1 定义在 (3.1) 式中, 则对任意 n∈Z+ 有
证 由假设 g∈A1 知 g1(J0)=J0,g2(J1)=J0 和 g(c1)=c1, 于是对任意 n∈Z+ 都有
从而 (3.2) 式为 g∈A1 的 n 次迭代.
定理3.2 若 g∈A2 定义在 (3.1) 式中, 且满足 g1,g2 是 C1 和扩张的, 则对任意 n∈Z+ 有
其中 i=0,1,⋯,2n−1, q 是满足共轭方程 g∘q=q∘T 的保向同胚解以及
证 由文献 [4,定理 2.7] 可知, 若 g 满足假设条件, 则一定存在逐段线性映射 T 与之拓扑共轭, 即共轭方程 g∘q=q∘T 存在保向同胚解 q:I→I, 其中 T:I→I 定义在 (3.4) 式中, 从而
至于映射 T 的 n 次迭代, 由文献 [7,引理 2.3] 有
特别地, 我们可以验证当 n=2 时, S(T2)={14,12,34}, 于是归纳可得 N(Tn)=2n−1 以及 S(Tn)={12n,22n,⋯,2n−12n}, 并计算可得
其中 [i+12] 表示对 i+12 取整, 进一步将其代入 (3.5) 式即可得 (3.3) 式为 g 的 n 次迭代.
注3.1 若 g∈A2 不满足在极大单调区间上扩张, 则其非单调点的原像在 I 中未必稠密, 从而共轭方程 g∘q=q∘T 的保向同胚解的存在性难以验证. 对于 g∈A2 且 g 更一般的情形, 其非单调点的存在情况在 n 次迭代后就会变得非常复杂.
定理3.3 若 g∈A3 且定义在 (3.1) 式中, 则对任意 n∈Z+ 有 gn(x)=g2n−k∘g1k(x),x∈[αk,αk−1],k=0,1,⋯,n, 其中 αk={g−k1(c1),k=0,1,⋯n−1,0,k=n.
证 第一步: 计算 S(gn).
我们断言
由于 g∈A3, 故 g(0)=0,g(c1)=1,g(1)=c1, 从而可验证 g(J0)=I,g(J1)=J1 且 g 分别在 J0 和 J1 上单调递增和递减. 故存在 1∈J1 和唯一 α1=g−11(c1)∈J0 使得 g(1)=g(α1)=c1. 而 1 是区间端点, 故由 (3.6) 式知
又因 α1<c1 且 g 在 J0 上严格递增, 故存在唯一 α2∈(0,α1) 使得 g2(α2)=g(α1)=c1, 即
从而利于归纳总结可证得断言成立. 特别地从证明过程中还有对任意 k=1,2,⋯,n−1 都有 αk<αk−1 和 g(αk)=αk−1.
第二步: 利用 S(gn) 中的点划分区间并研究区间相关性质.
令 J0k:=[αk,αk−1], 其中 k=1,2,⋯,n, 则由 (3.7) 式和 αn=0 知 J0=⋃nk=1J0k. 当 k=1 时, 由 g(α1)=α0=c1 和 g(c1)=1 知 g(J01)=J1. 当 k∈{2,3,⋯,n−1} 时, 由 g(αk)=αk−1 我们有
当 k=n 时, 由 g(0)=0 知 g(J0n)=g([αn,αn−1])=g([αn−1])=[αn−2], 进而
第三步: 计算 gn.
首先由 g(J1)=J1 知对任意 x∈J1 有 gn(x)=gn2(x). 当 k=1 时, 由第二步中 g(J01)=J1 知对任意 x∈J01 有gn(x)=gn−1∘g(x)=gn−12∘g1(x). 当 k∈{2,3,⋯,n−1} 时, 由 (3.8) 式可知对任意 x∈J0k 有 gn(x)=gn−k2∘gk1(x). 当 k=n 时, 由 (3.9) 式可知对任意 x∈J0n 有 gn(x)=gn1(x). 由上我们可归纳总结为
其次易验证 I=J0∪J1=⋃nk=1J0k∪J1, 从而 (3.10) 式即为 g∈A3 的 n 次迭代.
定理 3.1-3.3 得到了当 g∈A 满足 g(0)=0 且 g(1)≠1 时 g 的迭代的具体表达式. 接下来我们利用共轭的方法给出 h∈A 满足 h(0)≠0 且 h(1)=1 时 h 的迭代.
注3.2 现给定任意映射 h∈A 且 h(1)=1, 其非单调点集为 S(h)={d1,d2,⋯,dN(h)} 以及 d0=0, dN(h)+1=1. 令 g(x):=ϕ−1∘h∘ϕ(x),∀x∈[0,1], 其中 ϕ(x)=1−x, 即 g(x)=1−h(1−x). 首先易验证 g(0)=0 以及对任意 i=0,1,⋯,N(h)+1 都有 ci:=1−di 为 g 的所有非单调点和端点. 其次由 h 是 Markov 映射我们知道所有 di 在 h 作用下的正半轨是有限的, 那么由 g(ci)=1−h(di) 知 ci 在 g 作用下的正半轨也是有限的, 即 g∈A 且满足定理 3.1-3.3, 进而
4 g∈B 的情形
接下来讨论 g∈B 的情形, 即 g 是一个可拼接的 Markov 映射且满足 g(0)=0 和 g(1)=1. 若 g 定义在 (2.3) 式中, 则由 g(0)=0 知 g 在 J0=[c1]=[c0,c1] 上单调递增. 又因为 g(1)=1, 所以 g 在 JN(g)=[cN(g),1] 上也单调递增, 这暗示了 N(g) 为一个偶数. 因此我们讨论 g∈B 且 N(g)=2 的情形, 即 S(g):={c1,c2}. 令
图4.1
图4.2
图4.3
图4.4
下面我们将分别给出这 4 类映射的正整数 n 次迭代.
定理4.1 若 g∈B1 定义在 (4.1) 式中且 g(c1)=c1, 则对任意 n∈Z+ 有
其中对所有 k=0,1,⋯n−1 有 α2k−1=g3−k(c1) 和 α2k=g3−k(c2).
证 第一步: 计算 S(gn).
我们断言
在假设 g∈B1 下我们可验证
且 g 在 J0 和 J2 上递增, 在 J1 上递减, 那么一定唯一存在 α1=g−13(c1)∈J2 和 α2=g−13(c2)∈J2 使得g(α1)=c1,g(α2)=c2. 此外由 g 在 J2 上单调递增我们有 α1<α2, 从而由 (3.6) 式知
又因 α−1<α0<α1<α2 且 g([α1,α2])=[c1,c2], 故由 (4.4) 式知存在唯一 α3,α4∈(α2,1)⊂J2 使得 g2(α3)=g(α1)=c1,g2(α4)=g(α2)=c2, 同样易验证 α3<α4 以及
从而归纳可得断言成立. 此外从证明过程中还知对任意 k=1,2,⋯,2n−2 有
第二步: 利用 S(gn) 中的点划分区间并研究区间相关性质.
令 J2k:=[αk,αk+1], 其中 k=0,1,⋯,2n−3, 则由 (4.3) 式知 J2=(⋃nk=0J2k)∪[α2n−2,1]. 当 k=0 时, 由 g(α0)=0 和 g(α1)=c1 可知 g(J20)=J0. 当 k=1 时, 由 g(α1)=c1 和 g(α2)=c2 知 g(J21)=J1. 当 k∈{2,3,⋯,2n−3} 时, 由 (4.5) 式有 g(J2k)=J2k−2 以及
其中 j=1,2,⋯,n−1. 此外当 x∈[α2n−2,1] 时, 由 g∈B1 知 g(1)=1, 从而
第三步: 计算 gn.
首先由 (4.4) 式有对任意 x∈J0 有 gn(x)=gn1(x); 对任意 x∈J1 有 gn(x)=gn−11∘g2(x).
当 k=0 时, 由 g(J20)=J0 知对任意 x∈J20 有 gn(x)=gn−1∘g(x)=gn−11∘g3(x).
当 k=1 时, 由 g(J21)=J1 知对任意 x∈J21 有 gn(x)=gn−1∘g(x)=gn−21∘g2∘g3(x).
当 k=2j−2,j∈{1,2,⋯,n−1} 时, 由 (4.6) 式知对任意 x∈J22j−2 有 gn(x)=gn−j1∘gj3(x).
当 k=2j−1,j∈{1,2,⋯,n−1} 时, 由 (4.6) 式知对任意 x∈J22j−1 有 gn(x)=gn−j−11∘g2∘gj3(x).
当 x∈[α2n−2,1] 时, 由 (4.7) 式知对任意 x∈[α2n−2,1] 有gn(x)=gn3(x).
其次易验证
从而 (4.2) 式就是 g∈B1 时的 n 次迭代.
类似于注记 3.2, f∈B1 且 f(c2)=c2 时的情形可通过共轭转化为 g∈B1且g(c1)=c1 时的情形得到其整数次迭代.
定理4.2 若 g∈B2 且定义在 (4.1) 式中, 则对任意 n∈Z+ 有
其中当 k=0,1,⋯,n−1 时 α1k=g1−k(c1), α2k=g3−k(c2), 当 k=n 时 α1n=0,α2n=1.
证 第一步: 计算 S(gn).
由 g∈B2 知 g(J1)=J1 且 g 在 J1 上单调递减, 故不存在 x0∈(c1,c2) 使得 g(x0)=c1 或 c2. 此外还有 g(J0)=J0∪J1, g(J2)=J1∪J2, 则存在唯一 α11∈J0 使得 g1(α11)=c1 和唯一 α21∈J2 使得 g3(α21)=c2, 进而类似于定理 3.3 证明过程第一步可得
满足 0=α1n<α1n−1<⋯<α11<α10=c1<c2=α20<α21<⋯<α2n−1<α2n=1 以及当 k=1,2⋯,n−1 时有 g1(α1k)=α1k−1 和 g3(α2k)=α2k−1.
第二步: 利用 S(gn) 中的点划分区间并研究区间相关性质.
令 J0k:=[α1k,α1k−1],J2k:=[α2k−1,α2k], 其中 k=1,2,⋯,n. 由 (4.9) 知 J0=⋃nk=1J0k 和 J2=⋃nk=1J2k. 此外由 g1(α1k)=α1k−1 和 g3(α2k)=α2k−1 可得
其中 k=1,2,⋯,n−1. 特别地, 当 k=n 时,
第三步: 计算 gn.
类似于定理 3.3 证明过程第三步可得: 当 x∈J0 时, 由 (4.10) 和 (4.12) 知对任意 x∈[α1k,α1k−1] 和任意 k=1,2,⋯,n 有 gn(x)=g2n−k∘g1k(x). 当 x∈J1 时, 由 g(J1)=J1 知对任意 x∈J1 有 gn(x)=gn2(x). 当 x∈J2 时, 由 (4.11) 和 (4.12) 式知对任意 x∈[α2k−1,α2k] 和任意 k=1,2,⋯,n 有 gn(x)=g2n−k∘g3k(x). 其次易验证
从而 (4.8) 式就是 g∈B2 时的 n 次迭代.
定理4.3 若 g∈B3 定义在 (4.1) 式中满足 g1,g2,g3 是 C1 且扩张的, 则对任意 n∈Z+ 有
其中 i=0,1,⋯,3n−1, q 是满足共轭方程 g∘q=q∘T 的保向同胚解以及
证 同定理 3.2 的证明类似可得.
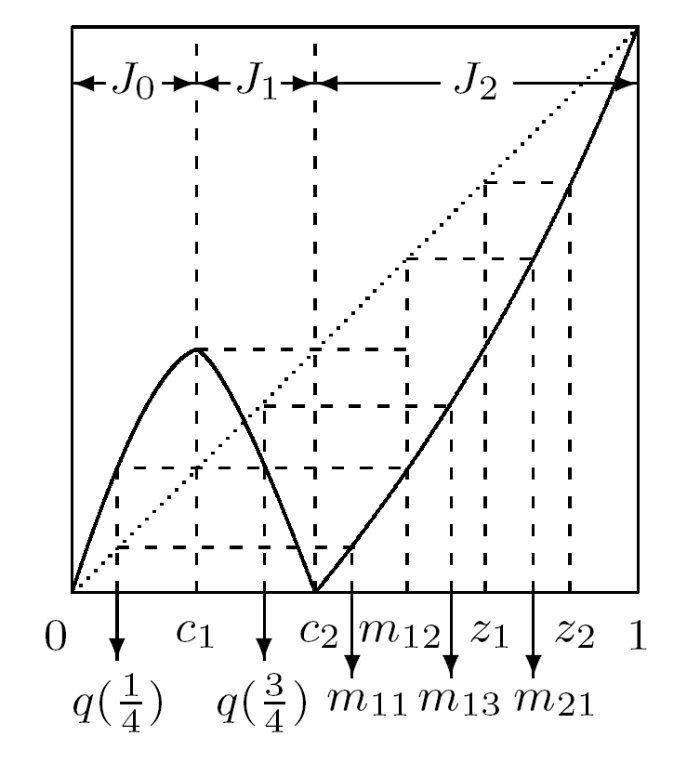
定理4.4 若 g∈B4 定义在 (4.1) 式中满足 g(c1)=c2,g(c2)=0 且 g1,g2 是 C1 并扩张的, 则对任意 n∈Z+ 有
其中 k=0,1,⋯,2n−1, q 定义在定理 3.2 中并且 mij=g−i3∘q(j2n−i), i=1,2,⋯,n−1,j=0,1,⋯,2n−i−1.
证 令 h:=g|J0∪J1, 则易验证 h 为自映射且满足定理 3.2, 从而可得其在 J0∪J1 上的 n∈Z+ 次迭代.
故接下来我们主要考虑 g 在 J2 上的非单调点情况.
由于 g(J0∪J1)=J0∪J1, g(J2)=I 且 g 在 J2 上单调递增, 故与定理 4.1 中证明的第一步 αk 且 k 为偶数时的生成方式一致 (如图 4.5, z1 为 c2 的一个原像, z1 的原像只会在其右侧产生为 z2), 存在点列
以及 gi([zi−1,zi])=gi−1([zi−2,zi−1])=⋯=[c2]. 于是可初步得到
然而与定理 4.1 不一致的是 c1 不仅会在 J2 产生原像, 还会在 J0 和 J1 上产生, 而 J0 和 J1 上的点在 J2 上亦有原像 (如图 4.5, c2 的原像为 c1 和 z1, 而 c1 的原像有 q(14),q(34) 和 m12), 故增加了定理证明的困难. 接下来我们就考虑这些新产生的非单调点. 由定理 3.2 可知,
图4.5
其中 j=0,1,⋯,2n−i−1, 从而有 S(gn−i)∩(0,c2)={q(j2n−i)|j=1,2,⋯,2n−i−1}. 又因为对任意 i=1,2,⋯,n−1 都有 gi([zi−1,zi])=gi3([zi−1,zi])=[c2], g(J2)=I 且 g 在 J2 上单调递增, 故一定存在唯一 mij∈[zi−1,zi] 使得 gi(mij)=q(j2n−i), 即 mij=g−i3∘q(j2n−i). 利用单调性易验证点列满足
且 gi([mij,mij+1])=[q(j2n−i),q(j+12n−i)], 从而有
其中 j=1,2,⋯,2n−i−1. 此外类似于 (3.9) 式, 由 g(1)=1 和当 i=1,2,⋯,n−1 时有 g(zi)=zi−1 知当 x∈[zn−1,1] 时, gn(x)=gn3(x). 得证.
类似于注记 3.2, f∈B4 且 f(c1)=1,f(c2)=c1 的情形可通过共轭转化为 g∈B4 且 g(c1)=c2,g(c2)=0 时的情形得到其整数次迭代.
5 可分映射的迭代及举例
由定义 2.1 可知, 可分映射可以划分为有限多个可拼接自映射, 从而其迭代可以转化这些自映射的迭代. 而一类特殊的 Markov 可拼接映射的迭代在第 3 节和第 4 节已经给出, 故接下来我们将用一个例子刻画可分映射的迭代.
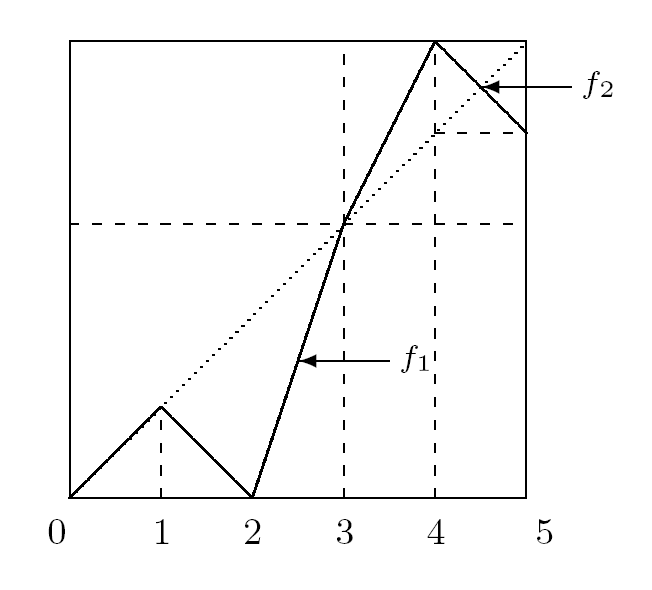
例5.1 定义
易验证 f(3)=3 以及 f([0,3])⊂[0,3] 和 f([3,5])⊂[3,5]. 则由定义 2.1 可知 f 为可分映射, x=3 为其可分不动点且可分为可拼接自映射. 令 f1=f|[0,3] 和 f2=f|[3,5], 则 f1∈B1,f2∈A3 (见图 5.1). 接下来我们分别计算 f1 和 f2 的迭代. 首先易验证 f1∈B1 且 S(f1)={c1:=1,c2:=2}, 则由定理 4.1 的断言 (4.3) 式可知 S(f31)={α−1,α0,α1,α2,α3,α4} 且满足
图5.1
于是利用定理 4.1 可得其 3 次迭代. 其次易验证 f2∈A3 且 S(f2)={4}, 类似利用定理 3.3 有 S(f32)={α0=4,α1=72,α2=134}, 进而可得其 3 次迭代. 综上可得 f 的 3 次迭代结果为
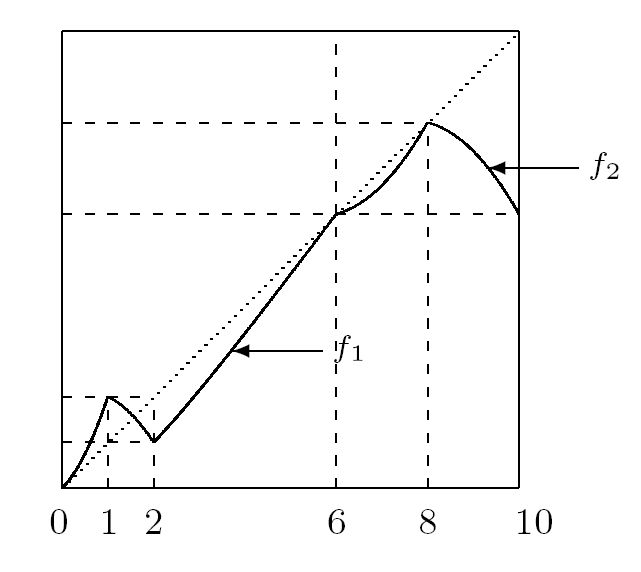
例5.2 定义
易验证 f(6)=6 以及 f([0,6])⊂[0,6] 和 f([6,8])⊂[6,8]. 则由定义 2.1 可知 f 为可分映射, x=6 为其可分不动点且可分为可拼接自映射. 令 f1=f|[0,6] 和 f2=f|[6,8], 则 f1∈B2,f2∈A1 (见图 5.2). 接下来我们分别计算 f1 和 f2 的迭代. 首先易验证 f1∈B2 且 S(f1)={c1:=1,c2:=2}, 则由定理 4.2 的断言 (4.9) 式可知 S(f31)={α10,α11,α12,α20,α21,α22} 且满足
图5.2
于是利用定理 4.2 可得其 3 次迭代. 其次易验证 f2∈A1 且 S(f2)={8}, 利用定理 3.1 可得其 3 次迭代. 综上可得 f 的 3 次迭代结果为
其中
参考文献
Topological conjugacy and transitivity for a class of piecewise monotone maps of the interval
A note on invariant measures for Markov maps of an interval
Topological conjugacies of piecewise monotone interval maps
Inducing, slopes, and conjugacy classes
Iterative roots of piecewise monotonic functions of nonmonotonicity height not less than 2
Nonlinear Anal,
On iterated maps of the interval
Invariant measures for Markov maps of the interval
区间上满的扩张 Markov 自映射的迭代根
Iterative roots of expanding Markov surjective self-maps on intervals
非特征端点条件下 PM 函数的迭代根
Characteristic endpoints question for piecewise monotone functions
Discussion on polynomials having polynomial iterative roots
论逐段单调连续函数的迭代根
DOI:10.12386/A1983sxxb0043
[本文引用: 1]

设E是一个集,f和g是将E映射到自身的函数.f~og表示f和g的复合函数(f~og)(x)=f(g(x)),x∈E.f的迭代函数f~n的定义是 f~o(x)=x,f~(n+1)=fof~n,n=0,1,2,….如果对一个整数r≥2和一切x∈E成立着 f~r=g,我们就说f是g的一个r阶的迭代根. 关于迭代根的研究至少可以上溯到Abel,甚至更早的Babbage.多年以来这问题一直引起许多作者的注意.1950年R.Isaacs在一篇精辟的论文中完成了一个奠基
Iterative roots of a piecewise monotone continuous self-mapping
DOI:10.12386/A1983sxxb0043
[本文引用: 1]

设E是一个集,f和g是将E映射到自身的函数.f~og表示f和g的复合函数(f~og)(x)=f(g(x)),x∈E.f的迭代函数f~n的定义是 f~o(x)=x,f~(n+1)=fof~n,n=0,1,2,….如果对一个整数r≥2和一切x∈E成立着 f~r=g,我们就说f是g的一个r阶的迭代根. 关于迭代根的研究至少可以上溯到Abel,甚至更早的Babbage.多年以来这问题一直引起许多作者的注意.1950年R.Isaacs在一篇精辟的论文中完成了一个奠基