1 引言
事件触发控制作为一种离散时间状态反馈控制, 因其资源利用的高效性和强反馈性引起了学者们的广泛关注[16⇓⇓-19]. 事件触发控制不同于传统的时间触发控制, 不需要固定的周期采样和传输.事件触发控制器通常由反馈控制器和触发条件组成, 采用触发阈值来确定采样和更新的时间, 仅当满足触发条件时信息传输才会进行. 文献 [20] 通过提出一种鲁棒动态事件触发状态观测器, 研究了受未知时变延迟影响的递归神经网络的事件触发状态估计问题. 文献 [21] 在动态和静态事件触发控制下, 讨论了具有多时滞的连续随机系统的镇定问题. 文献 [22] 中利用事件触发机制对采样信号进行滤波, 降低网络带宽占用和资源传输速率, 解决了非线性网络系统的滑模控制问题. 文献 [23]在事件触发控制下讨论了具有随机不确定性和非线性的半马尔可夫跳跃系统的随机稳定性.
受上述讨论启发, 本文采用输入到状态稳定理论和事件触发机制, 并利用 Lyapunov 函数和线性矩阵不等式方法, 研究时滞随机非线性系统的控制问题. 本文的主要贡献如下
(1) 对于许多实际的非线性系统, 往往受到不确定性和外部干扰的影响. 针对此问题, 本文探究了一类带有参数不确定和随机外部干扰的非线性系统事件触发控制问题.
(2) 为了减少事件触发频率和避免 Zeno 行为, 本文设计了一种事件触发控制器. 相比传统的事件触发方法, 本文在事件触发条件中加入指数衰减项, 不仅能量化状态轨迹收敛率, 同时能减少事件触发频率; 此外, 在每个触发时刻之后加入控制暂停区间, 从技术上排除 Zeno 行为.
2 预备知识
方便起见, 本文使用以下符号.
考虑下列具有不确定性和外部干扰的随机非线性系统
这里
注 2.1
其中
考虑的事件触发机制如下
这里
注 2.2 基于事件触发控制机制(2.3), 在任意两个连续的触发时刻之间引入一个控制暂停区间
状态反馈控制器如下
其中
因此, 系统(2.1)可以改写成
本文设计的事件产生函数
这里
下面将引入一些本文需要用到的引理与定义.
引理 2.1[24] 对任意
这里
引理 2.2[25] 对于任意
其中
引理 2.3[26] 令
假设 2.1 存在常数对角矩阵
其中
定义 2.1 对任意
那么系统(2.6)是均方指数输入到状态稳定.
3 主要结论
在本节中, 证明具有不确定性和外部扰动的随机时变时滞非线性系统 (2.6) 是均方指数输入到状态稳定. 最后, 利用事件触发机制, 得到任意两个连续触发时刻间隔的下界, 排除 Zeno 行为.
定理 3.1 如果对于事件触发参数
其中
证 首先定义一个 Lyapunov 函数:
根据引理2.1 存在常数
通过引理 2.2 和假设 2.1 存在正定矩阵
将(3.4)-(3.10)式代入(3.3)式可得
此外, 根据事件触发控制机制对任意
因此
这意味着
现在取
利用 Dynkin 公式和引理 2.3 有
定义一个函数
结合引理 2.3 和(3.15)式有
然后,可得
这里
证毕.
定理 3.2 对于事件触发参数
其中
证 对 (3.18) 式两边同时乘以矩阵
因为(3.18)式小于 0, 令
显然, 由(3.17)式可以得到(3.2)式, 线性矩阵不等(3.18)能推出(3.1)式, 通过定理3.1, 定理 3.2 可以得证.
4 算例仿真
在本节中, 为证实结果的有效性, 考虑三种情况: 系统无控制
其中
其中非线性函数
4.1 单系统
当
图1
4.2 带有控制 u(t) 的系统
令
反馈增益矩阵
图2
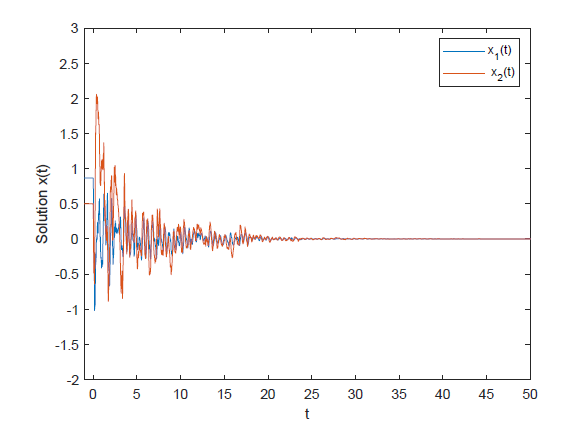
4.3 带有干扰 \vartheta(t) 和控制 u(t) 的系统
令外部扰动
图3
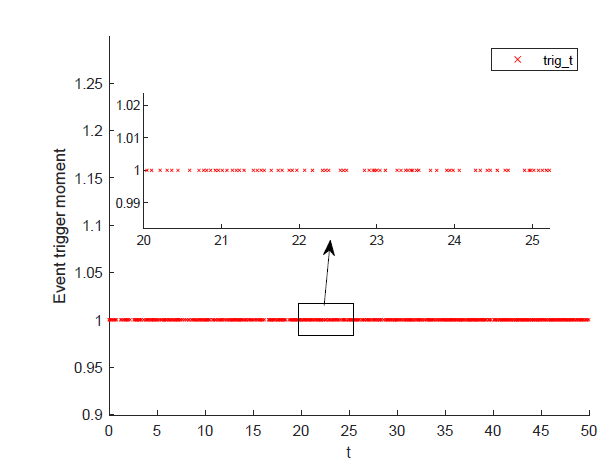
图4
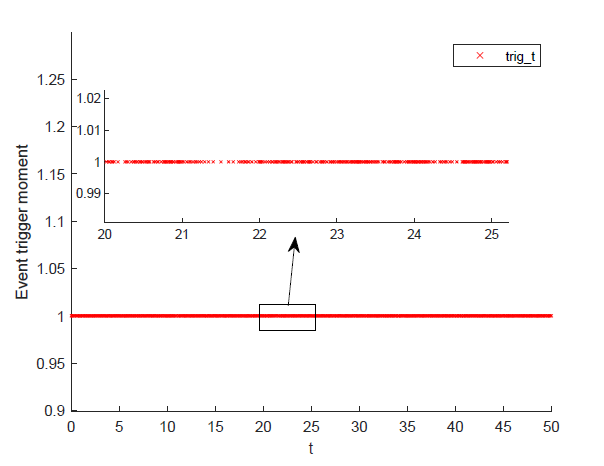
图5
5 小结
本文研究具有外部扰动和不确定性的随机时变时滞微分非线性系统的事件触发控制及其稳定问题. 首先, 采用间歇事件触发控制机制排除 Zeno 行为, 并在事件产生函数中加入指数衰减项, 进一步降低事件触发频率. 然后, 利用线性矩阵不等式方法, 结合事件触发机制获得系统稳定的判据, 通过算例 4.1, 4.2 和 4.3 证实了方法的有效性.
参考文献
Stability of time-varying hybrid stochastic delayed systems with application to aperiodically intermittent stabilization
Razumikhin-type theorems on polynomial stability of hybrid stochastic systems with pantograph delay
Adaptive output feedback control for stochastic uncertain nonlinear time-delay systems
Improved Razumikhin and Krasovskii stability criteria for time-varying stochastic time-delay systems
Smooth stabilization implies coprime factorization
Adaptive partial-state feedback control for stochastic high-order nonlinear systems with stochastic input-to-state stable inverse dynamics
Input-to-state stability of nonlinear systems: Event-triggered impulsive control
Stabilizability of time-varying switched systems based on piecewise continuous scalar functions
一类具有时滞及反馈控制的非自治非线性比率依赖食物链模型
On a nonlinear non-autonomous ratio-dependent food chain model with delays and feedback controls
一类具有多变时滞的非线性微分系统的周期解与稳定性
利用Chapman-Kolmogorov等式和基本解矩阵、状态转移矩阵的概念,并结合Floquet理论,研究一类具有多变时滞的非线性中立型微分系统.首先,通过适当的积分变换得到系统解一个新的表达式.然后,利用Krasnoselskii不动点定理,给出了系统周期解的存在性,并在一定条件下构造适当的压缩映射得到该系统周期解的唯一性和零解稳定性的充分条件,改进了已有文献中的相应结果.
Periodic solutions and stability of a class of nonlinear differential system with variable delays
利用Chapman-Kolmogorov等式和基本解矩阵、状态转移矩阵的概念,并结合Floquet理论,研究一类具有多变时滞的非线性中立型微分系统.首先,通过适当的积分变换得到系统解一个新的表达式.然后,利用Krasnoselskii不动点定理,给出了系统周期解的存在性,并在一定条件下构造适当的压缩映射得到该系统周期解的唯一性和零解稳定性的充分条件,改进了已有文献中的相应结果.
Stability analysis of uncertain sampled-data systems with incremental delay using looped-functionals
Tutorial on Lyapunov-based methods for time-delay systems
Output-feedback control for stochastic nonlinear systems subject to input saturation and time-varying delay
Globally adaptive control for stochastic nonlinear time-delay systems with perturbations and its application
A note on guaranteed cost control for nonlinear stochastic systems with input saturation and mixed time-delays
Dynamic event-triggered distributed coordination control and its applications: A survey of trends and techniques
Event-based impulsive control of continuous-time dynamic systems and its application to synchronization of memristive neural networks
An overview and deep investigation on sampled-data-based event-triggered control and filtering for networked systems
An overview of recent advances in event-triggered consensus of multiagent systems
Event-triggered state estimation for recurrent neural networks with unknown time-varying delays
Event-triggered control for stochastic systems with multiple delays
Extended dissipative sliding mode control for nonlinear networked control systems via event-triggered mechanism with random uncertain measurement
Event-triggered control for networked nonlinear semi-markovian jump systems with randomly occurring uncertainties and transmission delay
Robust control of a class of uncertain nonlinear systems
Input-to-state stabilization of delayed differential systems with exogenous disturbances: The event-triggered case
On hybrid impulsive and switching systems and application to nonlinear control