1 引言
非线性现象在物理、化学、地质等自然学科中广泛出现, 许多非线性现象都可以用非线性偏微分方程 (NLPDEs) 来描述[1⇓-3]. 近年来, 越来越多的学者关注 NLPDEs 的非线性波解, 特别是孤子解[4,5]、Lump 解[6⇓-8]、呼吸解[9,10]. 尤其是由上述几种非线性波组成的相互作用解[11⇓⇓-14] 逐渐成为 NLPDEs 研究的热点问题. 通过研究不同非线性波之间的相互作用, 可以更全面地了解和分析复杂非线性现象的本质. 基于 Hirota 双线性方法[15⇓-17], 学者们提出了获得非线性波解的多种有效方法, 例如同宿测试法[18⇓-20]、 参数极限法[21]、 模共振技术[22,23]等.
本文要研究的方程为如下的新 (3+1) 维 KP 方程[24]
其中
本文主要研究方程 (1.1) 的较为复杂的非线性波解. 第 2 节, 基于 Hirota 双线性形式, 利用模共振技术将
2 由 N -孤子解转化为 P -呼吸解
不失一般性, 在方程 (1.1) 中取
得到了方程 (1.1) 的 Hirota 双线性形式
将辅助函数
其中
当
若 (2.3) 式中的参数满足如下的模共振约束条件
则 (2.3) 式转化为
其中
将 (2.6) 式和 (2.7) 式带入 (2.2) 式, 即可得到目标方程的
例 Ⅰ
此时,
其中
根据 (2.8) 式易知,
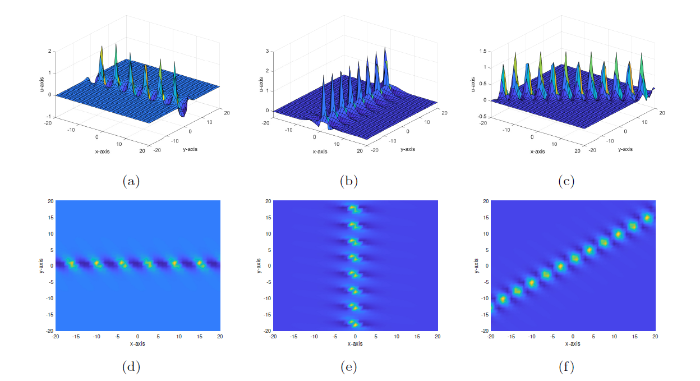
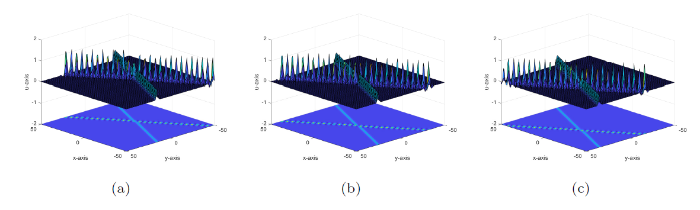
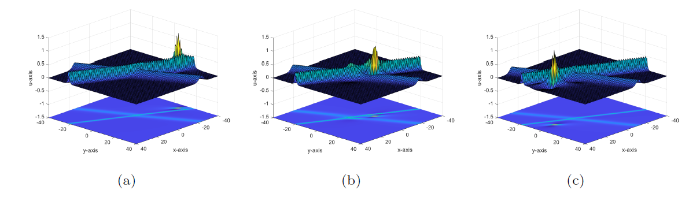
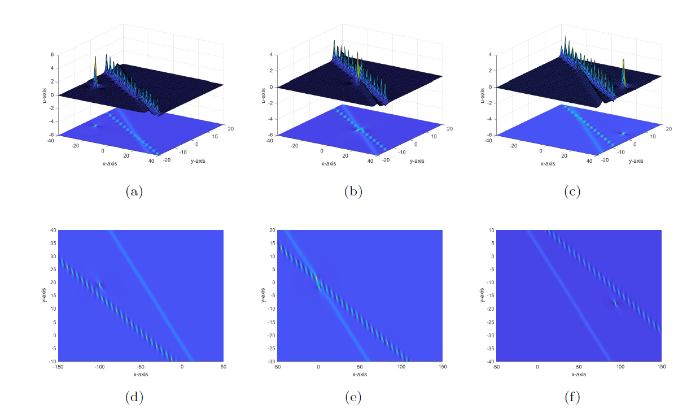
图1
图1
(a) (d) 平行于
例Ⅱ
此时, 辅助函数
其中
将 (2.12) 式带入 (2.1) 式, 且取
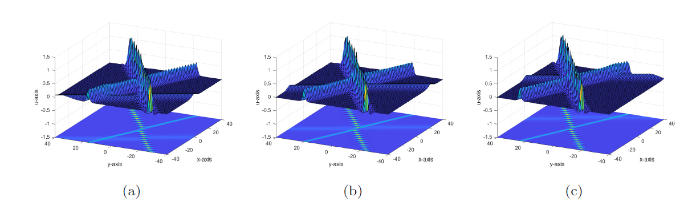
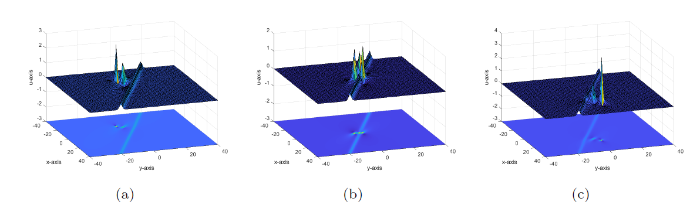
2-呼吸解随时间的演化过程如图2 所示.
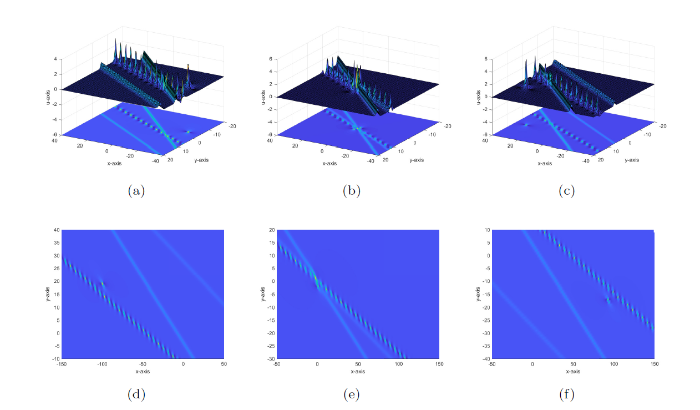
图2
3 Lump解
3.1 由同宿呼吸解退化为 Lump 解
根据文献 [18], 考虑将
其中
同宿呼吸解为
其中
取
图3
其中
3.2 由 N -孤子解退化为 Q -Lump 解
若对 (2.3) 式应用参数极限法[23], 则
其中
例 Ⅰ
此时, (3.4) 式为
其中
将 (3.5) 式带入 (2.1), 且取
其中
由 (3.6) 式和 (3.7) 式易得 1-Lump 解得速度分量为
在
处达到最小值
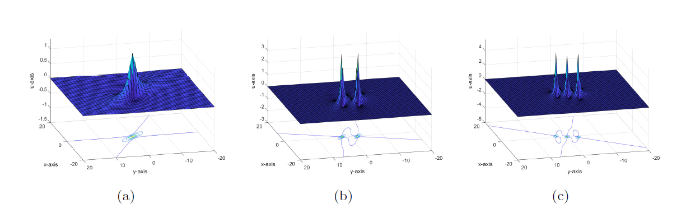
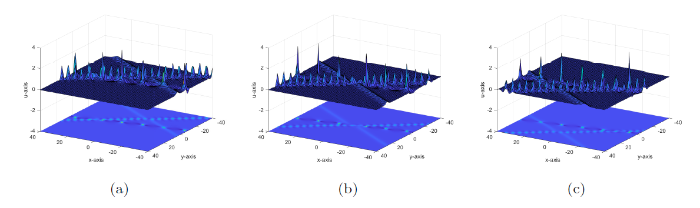
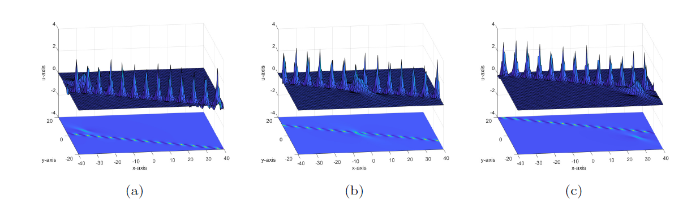
图4
例Ⅱ
2-Lump 解的辅助函数
其中
取
2-Lump 解如图4(b) 所示.
例Ⅲ
当
3-Lump 解如图4(c) 所示.
观察图4可以发现, 1-Lump 解沿着 “直线” 向四周传播, 其在传播时, 形状、振幅不发生改变. 但是在 2-Lump 解、3-Lump 解中, 我们观察到, 只有在 Lump 波的边缘地带是沿 “直线” 传播的, 在 Lump 波中间交会的地方, 其传播方式变得 “弯曲”, 形状发生了改变. 这是由于在 Lump 波的内侧, 能量进行了转换从而引发了它们形状的变化. 这种情况在现实中可能会引起类似海啸、地震等灾难现象.
4 相互作用解
4.1 由 P -呼吸和 R -孤子组成的相互作用解
如果 (2.3) 式中的参数满足
其中
例Ⅰ
此时,
其中
将 (4.2) 式带入 (2.3) 式且取
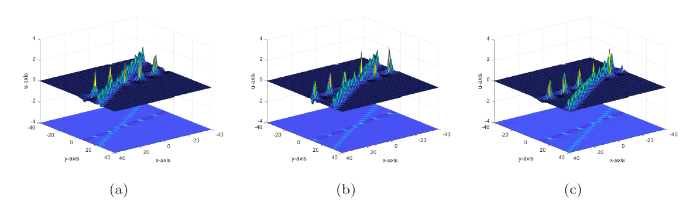
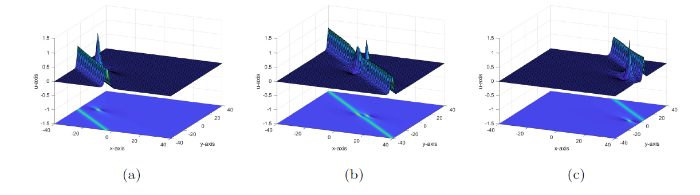
图5
例Ⅱ
当
1-呼吸与 2-孤子组成的混合解如图6 所示.
图6
例Ⅲ
同样地, 令
2-呼吸与 1-孤子随时间的动力学行为如图7 所示.
图7
4.2 由 Q -Lump 和 R -孤子组成的相互作用解
为构造出新 (3+1) 维 KP 方程的
例Ⅰ
1-Lump 与 1-孤子组成的相互作用解的辅助函数
其中
令
1-Lump 与 1-孤子的相互作用过程如图8 所示.
图8
例Ⅱ
此时, 辅助函数
其中
取
1-Lump 与 2-孤子的随时间的演化过程如图9 所示.
图9
例Ⅲ
当
其中
取
该相互作用过程如图10 所示.
图10
4.3 由 Q -Lump 和 P -呼吸组成的相互作用解
若 (2.3) 式中的参数满足如下的约束条件
可以得到目标方程的由
例Ⅰ
此情形下, (2.3) 式变为
其中
令
1-Lump 与 1-呼吸随时间的弹性碰撞过程如图11所示.
图11
例Ⅱ
当
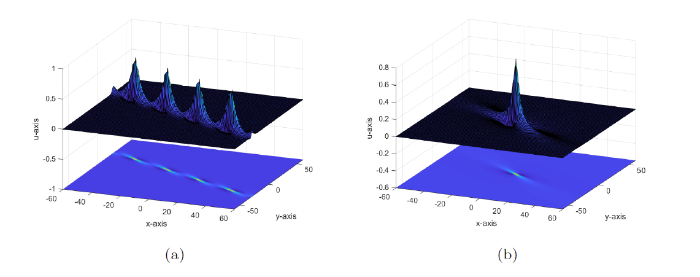
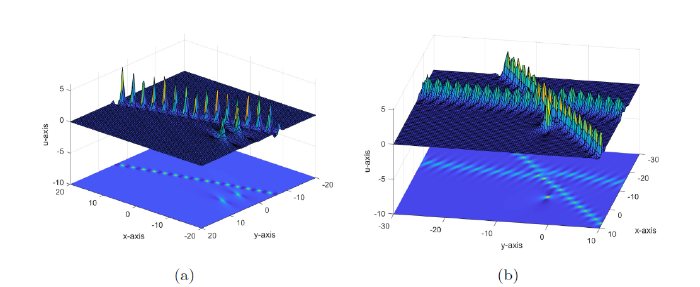
该相互作用解如图12(a) 所示.
图12
例Ⅲ
同样地, 当
1-Lump与 2-呼吸组成的相互作用解如图12(b) 所示.
4.4 由 Q -Lump, P -呼吸和 R -孤子组成的混合解
若对 (2.3) 式施加下列的约束条件
则可以得到方程 (1.1) 的由 Q-Lump、P-呼吸与 R-孤子这三种基本解组成的混合解.
例Ⅰ
1-Lump、1-呼吸与 1-孤子组成的混合解的辅助函数
其中
令
该相互作用过程如图13 所示.
图13
例Ⅱ
当
1-Lump、1-呼吸与 2-孤子的动力学行为如图14 所示.
图14
5 总结
本文得到了方程 (1.1) 的不同类型的非线性波解, 例如
最后, 通过
基于 Hirota 双线性方法[15⇓-17], 可通过同宿测试法[18⇓-20]、三波法[9,19] 和基于
参考文献
Exact solution of the Korteweg-de vries equation for multiple collisions of solitons
A nonlinear modification of the Schrödinger equation
Painlevé analysis for new (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equations with constant and time-dependent coefficients
Extend three-wave method for the (1+2)-dimensional Ito equation
Integrable (3+1)-dimensional Ito equation: variety of lump solutions and multiple-soliton solutions
Lump solutions to the Kadomtsev-Petviashvili equation
Lump and lump-multi-kink solutions in the (3+1)-dimensions
Various forms of lumps and interaction solutions to generalized Vakhnenko Parkes equation arising from high-frequency wave propagation in electromagnetic physics
Dynamics of multi-breathers, N-solitons and M-lump solutions in the (2+1)-dimensional KdV equation
Breather waves, rogue waves and complexiton solutions for a Zakharov-Kuznetsov equation
Degeneration of solitons for a (3+1)-dimensional generalized nonlinear evolution equation for shallow water waves
M-lump,high-order breather solutions and interaction dynamics of a generalized (2+1)-dimensional nonlinear wave equation
Degeneration of N-soliton solutions for a (3+1)-dimensional nonlinear model in shallow water waves
N-lump and interaction solutions of localized waves to the (2+1)-dimensional generalized KDKK equation
Exact envelope-soliton solutions of a nonlinear wave equation
Symmetry reduction and exact solutions of the (3+1)-dimensional nKdV-nCBS equation
N-soliton solutions and the Hirota conditions in (2+1)-dimensions
Bilinear Bäcklund transformation, kink and breather-wave solutions for a generalized (2+1)-dimensional Hirota-Satsuma-Ito equation in fluid mechanics
Some new kink type solutions for the new (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation
Dynamics of lump collision phenomena to the (3+1)-dimensional nonlinear evolution equation
Lump solutions and interaction solutions for (2+1)-dimensional KPI equation
Soliton molecules and some novel hybrid solutions for the (2+1)-dimensional generalized Konopelchenko-Dubrovsky-Kaup-Kupershmidt equation
Solitary wave, M-lump and localized interaction solutions to the (4+1)-dimensional Fokas equation
Painlevé analysis for a new (3+1)-dimensional KP equation: Multiple-soliton and lump solutions
Damped Kadomtsev-Petviashvili equation for weakly dissipative solitons in dense relativistic degenerate plasmas
Kadomtsev-Petviashvili equation in relativistic fluid dynamics
Dispersion-managed lump waves in a spatial symmetric KP model
Lump waves in a spatial symmetric nonlinear dispersive wave model in (2+1)-dimensions
Lump and interaction solutions to the (2+1)-dimensional Burgers equation
A novel kind of reduced integrable matrix mKdV equations and their binary Darboux transformations
Linear superposition of Wronskian rational solutions to the KdV equation
Four-component integrable hierarchies of Hamiltonian equations with (
Novel Liouville integrable Hamiltonian models with six components and three signs