Loading [MathJax]/jax/output/HTML-CSS/jax.js

数学物理学报, 2024, 44(6): 1511-1519

推广的导数非线性薛定谔方程的单/双周期背景上的呼吸子和怪波及其碰撞解

娄瑜,1, 张翼,2,*

1浙江工业职业技术学院公共基础教育部 浙江绍兴 312000

2浙江师范大学数学科学学院 浙江金华 321004

Breather and Rogue Wave on the Periodic/Double Periodic Background and Interaction Solutions of the Generalized Derivative Nonlinear Schr¨odinger Equation

Lou Yu,1, Zhang Yi,2,*

1Public Basic Education Department, Zhejiang Industry Polytechnic College, Zhejiang Shaoxing 312000

2Department of Mathematics, Zhejiang Normal University, Zhejiang Jinhua 321004

通讯作者: *张翼, Email: zy2836@163.com

收稿日期: 2023-11-30   修回日期: 2024-04-28  

基金资助: 国家自然科学基金(11371326)
国家自然科学基金(11975145)
国家自然科学基金(12271488)

Received: 2023-11-30   Revised: 2024-04-28  

Fund supported: NSFC(11371326)
NSFC(11975145)
NSFC(12271488)

作者简介 About authors

娄瑜,Email:530072461@qq.com

摘要

非线性薛定谔方程是物理和应用数学领域中一个非常重要的可积系统. 该文利用达布变换研究了推广的导数非线性薛定谔方程的单/双周期背景上的呼吸子和怪波以及呼吸子和怪波的碰撞解. 首先, 构造推广的导数非线性薛定谔方程的达布变换. 然后, 通过达布变换, 推导出周期背景和双周期背景上的呼吸子解和怪波解以及碰撞解. 最后, 借助于图示, 详细分析了有趣的新解结构. 这也为研究新型解的物理机制提供了理论依据.

关键词： 推广的导数非线性薛定谔方程; 达布变换; 周期解; 呼吸子; 怪波

Abstract

The nonlinear Schr¨odinger equation is a very important integrable system in the field of physics and applied mathematics. In this paper, the breather and rogue wave on the periodic/double periodic background and the collision solutions of breather and rogue wave for the generalized derivative nonlinear Schr¨odinger equation are studied by using the Darboux transformation. Firstly, the Darboux transformation of the generalized derivative nonlinear Schr¨odinger equation is constructed. Then, by using the Darboux transformation, the breather and rogue wave on the periodic/double periodic background and the collision solutions are derived. Finally, by means of the figures, the structures of interesting new solutions are analyzed in detail, which also provide a theoretical basis for studying the physical mechanism of the new solution.

Keywords： The generalized derivative nonlinear Schrödinger equation; Darboux transformation; Periodic solution; Breather; Rogue wave

PDF (3267KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

娄瑜, 张翼. 推广的导数非线性薛定谔方程的单/双周期背景上的呼吸子和怪波及其碰撞解[J]. 数学物理学报, 2024, 44(6): 1511-1519

Lou Yu, Zhang Yi. Breather and Rogue Wave on the Periodic/Double Periodic Background and Interaction Solutions of the Generalized Derivative Nonlinear Schr¨odinger Equation[J]. Acta Mathematica Scientia, 2024, 44(6): 1511-1519

1 引言

自然界中存在着许多极其复杂的动力学行为和非线性物理现象. 因此, 研究非线性发展方程的精确解的动力学行为是非线性科学和数学物理的重要内容[1⇓⇓⇓-5]. 非线性发展方程的精确解以各类孤子、呼吸子和怪波的形式存在. 孤子又称孤立波, 是一种在传播过程中形状、幅度和速度都维持不变的脉冲状行波. 呼吸子是由于平面背景上的小振幅扰动的不稳定性而产生的波, 可以分为两种类型: Akhmediev 呼吸子和 Kuznetsov-Ma (KM) 呼吸子[6⇓-8]. Akhmediev 呼吸子在时间方向上局域, 在空间方向上周期, 而 Kuznetsov-Ma 呼吸子在空间方向上局域, 在时间方向上周期. 特别地, 这两种呼吸子在极限行为下可以转化为怪波. 怪波是一种具有高振幅和在空间和时间上局域的波[9]. 值得关注的是, 孤子、呼吸子和怪波之间的碰撞可以产生更丰富的混合波结构和更有趣的动力学行为. 例如, 高以天教授借助于二元达布变换获得了非局域 Lakshmanan-Porsezian-Daniel 方程的孤子解以及孤子与周期解的碰撞解[10]; 耿献国教授利用达布变换研究了第三型耦合的导数非线性薛定谔方程的高阶怪波解[11], 等等. 为了更好地理解碰撞解在非线性动力现象中的物理机制, 人们使用了许多强大的方法来研究非线性发展方程的解, 如 Hirota 双线性方法[12,13], Bell 多项式[14,15], Riemann-Hilbert[16⇓⇓-19], 达布变换[20⇓⇓⇓-24], 等等.

该文研究如下推广的导数非线性薛定谔方程

iut+uxx−2i(2β−1)|u|2ux+(4β|u|4u−i(4β−1)u2u∗x−2iα(2ux+i|u|2u−2iαu)=0.
(1.1)

该方程可以约化几个著名的方程. 当 α=0 时, 方程 (1.1) 约化为 Kundu 方程[25]; 当 α=0,β=0 时, 方程(1.1) 约化为 Kaup-Newell 方程[26]; 当 α=0,β=14 时, 方程 (1.1) 约化为 Chen-Lee-Liu 方程[27]; 当 α=0,β=12 时, 方程 (1.1) 约化为 Gerdjikov-Ivanov 方程[28]. 目前, 方程 (1.1) 只研究了 positon 解和高阶怪波解[29]. 因此, 本文将应用达布变换研究方程 (1.1) 在周期背景上的呼吸子、怪波及其碰撞解.

2 推广的导数非线性薛定谔方程的达布变换

基于文献 [29], 方程 (1.1) 的 Lax 对为

Ψx=UΨ,U=(−iλ2+iβ|u|2+iαλu−λu∗iλ2−iβ|u|2−iα),Ψt=VΨ,V=(V1V2V3−V1),
(2.1)

其中

V1=−2iλ4+iλ2|u|2+i2β(8β−3)|u|4+β(−uxu∗+u∗xu)+4iαβ|u|2,V2=2λ3u+λ(iux+(2β−1)|u|2u+2αu),V3=−2λ3u∗+λ(iu∗x−(2β−1)|u|2u∗−2αu∗).
(2.2)

通过计算可知, 方程 (1.1) 的种子解为 u=ceiρ, 其中 ρ=ax+bt,b=(4β−1)βc4−(a−2α)c2−(a−2α)2.

接下来, 以定理的形式给出该方程的达布变换.

定理 2.1 新解 u[n] 可以借助于 n 重达布变换获得

u[n]=U211U221u+2iU11U12U221,
(2.3)

此处的 U11,U12,U21 根据 n 的奇偶性而具有不同的形式.

当 n=2k 时,

U11=|λn−11φ1λn−21ϕ1λn−31φ1⋯λ1φ1ϕ1λn−12φ2λn−22ϕ2λn−32φ2⋯λ2φ2ϕ2⋮⋮⋮⋮⋮⋮λn−1nφnλn−2nϕnλn−3nφn⋯λnφnϕn|,U12=|λn1ϕ1λn−21ϕ1λn−31φ1⋯λ1φ1ϕ1λn2ϕ2λn−22ϕ2λn−32φ2⋯λ2φ2ϕ2⋮⋮⋮⋮⋮⋮λnnϕnλn−2nϕnλn−3nφn⋯λnφnϕn|,U21=|λn−11ϕ1λn−21φ1λn−31ϕ1⋯λ1ϕ1φ1λn−12ϕ2λn−22φ2λn−32ϕ2⋯λ2ϕ2φ2⋮⋮⋮⋮⋮⋮λn−1nϕnλn−2nφnλn−3nϕn⋯λnϕnφn|,

当 n=2k+1 时,

U11=|λn−11φ1λn−21ϕ1λn−31φ1⋯λ1ϕ1φ1λn−12φ2λn−22ϕ2λn−32φ2⋯λ2ϕ2φ2⋮⋮⋮⋮⋮⋮λn−1nφnλn−2nϕnλn−3nφn⋯λnϕnφn|,U12=|λn1ϕ1λn−21ϕ1λn−31φ1⋯λ1ϕ1φ1λn2ϕ2λn−22ϕ2λn−32φ2⋯λ2ϕ2φ2⋮⋮⋮⋮⋮⋮λnnϕnλn−2nϕnλn−3nφn⋯λnϕnφn|,U21=|λn−11ϕ1λn−21φ1λn−31ϕ1⋯λ1φ1ϕ1λn−12ϕ2λn−22φ2λn−32ϕ2⋯λ2φ2ϕ2⋮⋮⋮⋮⋮⋮λn−1nϕnλn−2nφnλn−3nϕn⋯λnφnϕn|.

基于定理 2.1 并引入以下函数

(λj+δj)sϕj(x,t;λj+δj)=ϕs,j,0+ϕs,j,1δj+ϕs,j,2δ2j+⋯+ϕs,j,kδkj+⋯,(λj+δj)sφj(x,t;λj+δj)=φs,j,0+φs,j,1δj+φs,j,2δ2j+⋯+φs,j,kδkj+⋯,

ϕs,j,k=1k!∂k∂δkj[(λj+δj)sϕj(x,t;λj+δj)],φs,j,k=1k!∂k∂δkj[(λj+δj)sφj(x,t;λj+δj)],δj 是一个小参数. 由此, 得到以下定理

定理 2.2 令 λ2=−λ∗1=12(−√(4β−1)c2−2(a−2α)−ic). 当 n=2k 时, 设 λn−1=αn−1+iβn−1,λn=αn+iβn, 且 βn−1≠±βn. 当 n=2k+1 时, 设 λn=αn+iβn, 于是半简并达布变换可以写成如下形式

un=ˆU211ˆU221u+2iˆU11ˆU12ˆU221,

当 n=2k 时,

ˆU11=|φ[n−1,1]ϕ[n−2,1]φ[n−3,1]⋯φ[1,1,1]ϕ[1,0,1]φ[n−1,1]ϕ[n−2,1]φ[n−3,1]⋯φ[2,1,1]ϕ[2,0,1]⋮⋮⋮⋮⋮⋮φ[k−1]ϕ[k−1]φ[k−1]⋯φ[k−1]ϕ[k−1]φ[k−1]ϕ[k−1]φ[k−1]⋯φ[k−1]ϕ[k−1]λn−1n−1φn−1λn−2n−1ϕn−1λn−3n−1φn−1⋯λn−1φn−1ϕn−1λn−1nφnλn−2nϕnλn−3nφn⋯λnφnϕn|,ˆU12=|ϕ[n,1]ϕ[n−2,1]φ[n−3,1]⋯φ[1,1,1]ϕ[1,0,1]ϕ[n,1]ϕ[n−2,1]φ[n−3,1]⋯φ[2,1,1]ϕ[2,0,1]⋮⋮⋮⋮⋮⋮ϕ[k−1]ϕ[k−1]φ[k−1]⋯φ[k−1]ϕ[k−1]ϕ[k−1]ϕ[k−1]φ[k−1]⋯φ[k−1]ϕ[k−1]λnn−1ϕn−1λn−2n−1ϕn−1λn−3n−1φn−1⋯λn−1φn−1ϕn−1λnnϕnλn−2nϕnλn−3nφn⋯λnφnϕn|,ˆU21=|ϕ[n−1,1]φ[n−2,1]ϕ[n−3,1]⋯ϕ[1,1,1]φ[1,0,1]ϕ[n−1,1]φ[n−2,1]ϕ[n−3,1]⋯ϕ[2,1,1]φ[2,0,1]⋮⋮⋮⋮⋮⋮ϕ[k−1]φ[k−1]ϕ[k−1]⋯ϕ[k−1]φ[k−1]ϕ[k−1]φ[k−1]ϕ[k−1]⋯ϕ[k−1]φ[k−1]λn−1n−1ϕnλn−2n−1φnλn−3n−1ϕn⋯λn−1ϕnφn−1λn−1nϕnλn−2nφnλn−3nϕn⋯λnϕnφn|,

当 n=2k+1 时,

ˆU11=|φ[n−1,1]ϕ[n−2,1]φ[n−3,1]⋯ϕ[1,1,1]φ[1,0,1]φ[n−1,1]ϕ[n−2,1]φ[n−3,1]⋯ϕ[2,1,1]φ[2,0,1]⋮⋮⋮⋮⋮⋮φ[k]ϕ[k]φ[k]⋯ϕ[k]φ[k]φ[k]ϕ[k]φ[k]⋯ϕ[k]φ[k]λn−1nφnλn−2nϕnλn−3nφn⋯λnϕnφn|,ˆU12=|ϕ[n,1]ϕ[n−2,1]φ[n−3,1]⋯ϕ[1,1,1]φ[1,0,1]ϕ[n,1]ϕ[n−2,1]φ[n−3,1]⋯ϕ[2,1,1]φ[2,0,1]⋮⋮⋮⋮⋮⋮ϕ[k]ϕ[k]φ[k]⋯ϕ[k]φ[k]ϕ[k]ϕ[k]φ[k]⋯ϕ[k]φ[k]λnnϕnλn−2nϕnλn−3nφn⋯λnϕnφn|,ˆU21=|ϕ[n−1,1]φ[n−2,1]ϕ[n−3,1]⋯φ[1,1,1]ϕ[1,0,1]ϕ[n−1,1]φ[n−2,1]ϕ[n−3,1]⋯φ[2,1,1]ϕ[2,0,1]⋮⋮⋮⋮⋮⋮ϕ[k]φ[k]ϕ[k]⋯φ[k]ϕ[k]ϕ[k]φ[k]ϕ[k]⋯φ[k]ϕ[k]λn−1nϕnλn−2nφnλn−3nϕn⋯λnφnϕn|.

3 单/双周期背景上的呼吸子和怪波及其碰撞解

在这一部分, 我们将构造推广的导数非线性薛定谔方程的单/双周期背景上的呼吸子和怪波及其碰撞解. 基于种子解, 我们选择以下形式的特征函数

Ψj=(ϕjφj)=(e12i(θj+ρ)−i(2λ2j−2βc2+a−2α+hj)2cλje−12i(θj−ρ)e−12i(θj+ρ)−i(2λ2j−2βc2+a−2α+hj)2cλje12i(θj−ρ)),
(3.1)

其中

θj=hj[x+(2λ2j+(2β−1)c2−(a−α))t+2j−1∑l=0sljϵlj],hj=√4λ4j+((4−8β)c2+4(a−2α))λ2j+(−2βc2+a−2α)2.

最后, 通过取极限 ϵj→0 就可以得到方程 (1.1) 的解.

3.1 周期背景上的呼吸子和怪波

对于

n=3,λ1=12(√(4β−1)c2−2(a−2α)−ic),λ2=−λ∗1,λ3=α3+iβ3.

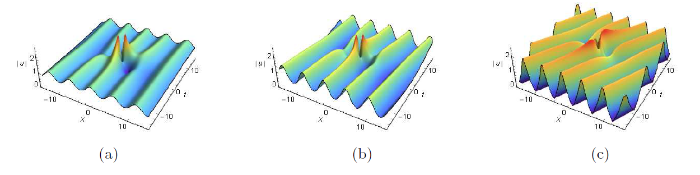
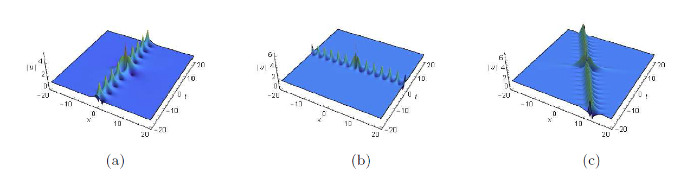
首先, 可以观察到图1 展示了周期背景上的怪波解. 在图1 中, 随着参数 β3 逐渐增长, 周期背景不仅振幅逐渐变大, 它的周期性也从以空间为周期逐渐转变成以时间和空间为周期. 值得关注的是, 与常见的怪波不同, 该周期背景上的怪波具有两个峰, 且每个峰的高度大约为 2. 产生此现象的原因是因为产生单峰的能量被分配于产生双峰, 这就导致双峰的峰值要低于正常的 3. 接下来, 图2 展示了周期背景上的呼吸子解, 在图2 中, 通过改变参数 α3 和 β3, 获得了三种不同类型的周期背景上的呼吸子解. 当 |α3|<12,|α3|<12 时, 获得了周期背景上的 Akhmediev 呼吸子; 当 |α3|>12,|α3|>12 时, 获得了周期背景上的 KM 呼吸子; 当 |α3|>12,|α3|<12 时, 获得了周期背景上的 Tajiri-Watanabe (TW) 呼吸子. 最后, 图3 展示了周期背景上的 TW 呼吸子解, 在图3 中, 随着参数 c 逐渐增大, 不仅 TW 呼吸子的周期逐渐变小, 呼吸子的角度也发生了变化.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   周期背景上的怪波解, 参数为 a=1,c=1,α=0,β=1,α3=0, (a) β3=110; (b) β3=310; (c) β3=35.


图2

新窗口打开| 下载原图ZIP| 生成PPT

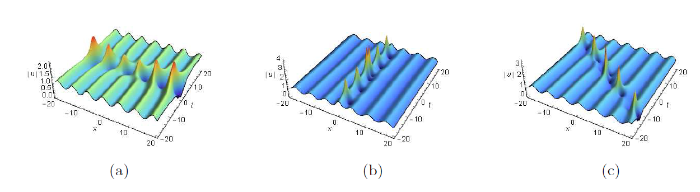
图2   周期背景上的呼吸子解, 参数为 a=1,c=1,α=0,β=1, (a) α3=310,β3=310; (b) α3=1120,β3=1120; (c) α3=1120,β3=920.


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   周期背景上的呼吸子解, 参数为 a=1,α=0,β=1,α3=0,β3=110, (a) c=110; (b) c=25; (c) c=45.


3.2 双周期背景上的呼吸子和怪波

对于 n=4,λ1=12(√(4β−1)c2−2(a−2α)−ic),λ2=−λ∗1,λ3=α3+iβ3,λ4=α4+iβ4. 固定 β3 和 β4 一个保持不变, 改变另一个的取值, 就可以获得不同的双周期背景上的怪波解. 在图4 中, 固定 β4, 由小到大改变 β3 的取值时就可以看到双周期背景由波浪形变为水滴形. 另一方面, 怪波的峰值也在发生改变, 当 β3=12 时, 怪波的峰值达到了 6. 此外, 改变 c 的取值, 可以得到另一类双周期背景上的怪波解. 在图5 中, 由小到大改变 c 的取值时就可以看到双周期背景也从波浪形转变成了水滴形, 同时, 怪波的峰值也在逐渐变大. 但是通过比较图4 和图5, 发现图5 的双周期的振幅要高于图4 中的双周期的振幅, 并且图5 中的怪波振幅明显低于图4 中的怪波振幅.

图4

新窗口打开| 下载原图ZIP| 生成PPT

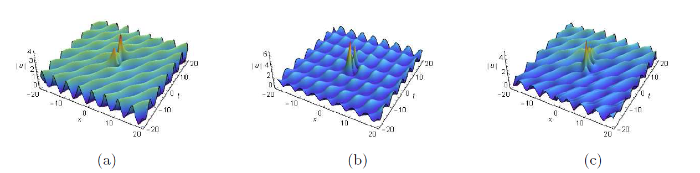
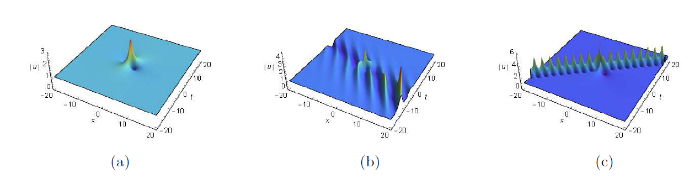
图4   双周期背景上的怪波解, 参数为 a=1,c=1,α=0,β=1,α3=0,α4=0,β4=−35, (a) β3=110; (b) β3=12; (c) β3=15.


图5

新窗口打开| 下载原图ZIP| 生成PPT

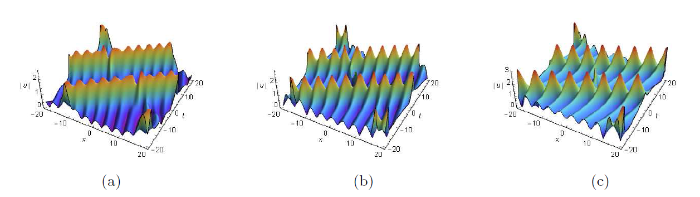
图5   双周期背景上的怪波解, 参数为 a=1,α=0,β=1,α3=0,α4=0,β3=35,β4=−12, (a) c=15; (b) c=12; (c) c=45.


3.3 呼吸子和怪波的碰撞解

对于 n=4,λ1=12(√(4β−1)c2−2(a−2α)−ic),λ2=−λ∗1,λ3=α3+iβ3,λ4=−λ∗3. 在此种情形下得到的是怪波与呼吸子的碰撞解. 在图6 中, 随着四个参数 a,c,α3,β3 同时改变就产生了三种不同类型的呼吸子和怪波的碰撞解, 即 KM 呼吸子与怪波的碰撞解, Akhmediev 呼吸子与怪波的碰撞解以及 TW 呼吸子与怪波的碰撞解. 在图7 中, 随着 |β3| 的逐渐变大, 呼吸子和怪波的形状变得越来越清晰明显, 并且两者的振幅也在变大. 值得注意的是, 当 β3=0 的时候, 呼吸子和怪波的碰撞解退化为了一阶怪波解, 可见图7(a).

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   呼吸子和怪波的碰撞解, 参数为 α=0,β=1, (a) a=1,c=1,α3=35,β3=−35; (b) a=94,c=32,α3=12,β3=−12; (c) a=85,c=85,α3=12,β3=−35.


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   呼吸子和怪波的碰撞解, 参数为 a=1,c=1,α=0,β=1,α3=35,(a) β3=0; (b) β3=−110; (c) β3=−15.


4 结论

该文研究了推广的导数非线性薛定谔方程的单/双周期背景上的呼吸子和怪波及其碰撞解. 首先给出该方程的奇数次和偶数次达布变换, 通过奇数次达布变换得到了周期背景上的呼吸子和怪波, 而通过偶数次达布变换得到了双周期背景上的呼吸子和怪波以及呼吸子和怪波的碰撞解. 随后, 根据三维图像详细分析了不同参数取值时解的构造和丰富的动力学行为. 有趣的是, 在图1中的怪波不同于常见的怪波, 它拥有两个峰, 且峰值均为 2. 这是因为产生单峰的能量被分配于产生双峰而导致双峰的峰值要低于正常的 3. 另一方面, 呼吸子呈现了三种类型: Akhmediev 呼吸子, KM 呼吸子和 TW 呼吸子. 这些碰撞解有利于理解更加复杂的物理现象. 此外, 在非线性发展方程中还存在另一种周期解, 也就是雅可比椭圆函数解. 因此, 后续论文我们将研究导数薛定谔方程在雅可比椭圆函数背景上的呼吸子和怪波.

参考文献

Olver P J, Sattinger D H. Solitons in Physics, Mathematics, and Nonlinear Optics. New York: Springer, 1990

[本文引用: 1]

Burger S, Bongs K, Dettmer S, Ertmer W, Sengstock K.

Dark solitons in Bose-Einstein condenstates

Phys Rev Lett, 1999, 83: 5198-5201

[本文引用: 1]

Bludov Y V, Konotop V V, Akhmediev N.

Matter rogue waves

Phys Rev A, 2009, 80: 033610

[本文引用: 1]

Yang B, Chen Y.

Dynamics of high-order solitons in the nonlocal nonlinear Schr¨odinger equations

Nonlinear Dynam, 2018, 94: 489-502

[本文引用: 1]

Ma W X.

Riemann-Hilbert problems of a six-component mKdV system and its soliton solutions

Acta Math Sci, 2019, 29(2): 509-523

[本文引用: 1]

Akhmediev N, Korbeev V I.

Modulation instability and periodic soulutions of the nonlinear Schr¨odinger equation

Theoret Math Phys, 1986, 69: 1089-1093

[本文引用: 1]

Kuznetsov E A.

Solitons in a parametrically unstable plasma

Dokl Akad Nauk SSSR, 1977, 236: 575-577

[本文引用: 1]

Priya N V, Senthilvelan M, Lakshmanan M.

Akhmediev breathers, Ma solitons and general breathers from rogue waves: A case study in the Manakov system

Phys Rev E, 2013, 88(2): 022918

[本文引用: 1]

Akhmediev N, Ankiewicz A, Taki M.

Waves that appear from nowhere and disappear without a trace

Phys Lett A, 2009, 373: 675-678

[本文引用: 1]

Wu X H, Gao Y T, Yu X, et al.

Binary Darboux transformation, solitons, periodic waves and modulation instability for a nonlocal Lakshmana-Porsezian-Daniel equation

Wave Motion, 2022, 114: 103036

[本文引用: 1]

Zhai Y Y, Ji T, Geng X G.

Coupled derivative nonlinear Schr¨odinger III equation: Darboux transformation and higher-order rogue waves in a two-mode nonlinear fiber

Appl Math Comput, 2021, 411: 126551

[本文引用: 1]

L¨u Xing, Chen S J.

Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: one-lump-multi-stripe and one-lump-multi-soliton types

Nonlinear Dynam, 2021, 103: 947-977

[本文引用: 1]

房春梅, 田守富.

约化的(3+1)维 Hirota 方程的呼吸波解、Lump 解和半有理解

数学物理学报, 2022, 42A(3): 775-783

[本文引用: 1]

Fang C M, Tian S F.

Breather Wave Solutions, Lump solutions and semi-rational solutions of a reduced (3+1) dimensional Hirota equation

Acta Math Sci, 2022, 42A(3): 775-783

[本文引用: 1]

Ma W X.

Bilinear equations and resonant solutions characterized by Bell polynomials

Rep Math Phys, 2013, 72(1): 41-56

[本文引用: 1]

Ma W X.

Trilinear equations, Bell polynomials, and resonant solutions

Front Math China, 2013, 8: 1139-1156

[本文引用: 1]

田守富.

一个广义导数非线性 Schr¨odinger 方程的 Riemann-Hilbert 问题: 长时间渐近行为

中国科学: 数学, 2022, 52(5): 505-542

[本文引用: 1]

Tian S F.

Riemann-Hilbert problem to a generalized derivative nonlinear Schr¨odinger equation: Long-time asymptotic behavior

Sci Sin Math, 2022, 52(5): 505-542

[本文引用: 1]

Wei H Y, Fan E G, Guo H D.

Riemann-Hilbert approach and nonlinear dynamics of the coupled higher-order nonlinear Schr¨odinger equation in the birefringent or two-mode fiber

Nonlinear Dynam, 2021, 104: 649-660

[本文引用: 1]

Chen X T, Zhang Y, Ye R S.

Riemann-Hilbert approach of the coupled nonisospectral Gross-Pitaevskii system and its multi-component generalization

Appl Anal, 2019, 100(10): 2200-2209

[本文引用: 1]

Hu B B, Xia T C, Ma W X.

Riemann-Hilbert approach for an initial-boundary value problem of the two-component modified Korteweg-de Vries equation on the half-line

Appl Math Comput, 2018, 332: 148-159

[本文引用: 1]

Guo B L, Ling L M, Liu Q P, Wu C F.

Nonlinear Schr¨odinger equation: generalized Darboux transformation and rogue wave solutions

Phys Rev E, 2012, 85: 026607

[本文引用: 1]

Wang X, Wei J.

Three types of Darboux transformation and general soliton soulutions for the space-shifted nonlocal PT symmetric nonlinear Schr¨odinger equation

Appl Math Lett, 2022, 130: 107998

[本文引用: 1]

Zhang Y, Ye R S, Ma W X.

Binary Darboux transformation and soliton solutions for the coupled complex modified Korteweg-de Vries equations

Math Meth Appl Sci, 2019, 43: 613-627

[本文引用: 1]

Fan E G.

Integrable evolution systems based on Gerdjikov-Ivanovequations, bi-Hamiltonian structure, finite-dimensional integrable systems and N-fold Darboux transforamtion

J Math Phys, 2000, 41: 7769-7782

[本文引用: 1]

Shen Y, Tian B, Zhou T Y, Gao X T.

N-fold Darboux transformation and solitonic interactions for the Kraenkel-Manna-Merle system in a saturated ferromagnetic material

Nonlinear Dynam, 2023, 111: 2641-2649

[本文引用: 1]

Kodama Y J.

Optical solitons in a monomode fiber

J Stat Phys, 1985, 39: 597

[本文引用: 1]

Chen J B, Pelinovsky D E, Upsal J.

Modulation instability of periodic standing waves in the derivative NLS equation

J Nonlinear Sci, 2021, 31: 58

[本文引用: 1]

Zhang N, Xia T C, Fan E G.

A Riemann-Hilbert approach to the Chen-Lee-Liu equation on the half line

Acta Math Appl Sin-E, 2018, 34: 493-515

DOI:10.1007/s10255-018-0765-7      [本文引用: 1]

In this paper, the Fokas unified method is used to analyze the initial-boundary value for the ChenLee-Liu equation<br/>i<i>&#8706;</i><sub><i>t</i></sub><i>u</i> + <i>&#8706;</i><sub><i>xx</i></sub><i>u</i>-i|<i>u</i>|<sup>2</sup><i>&#8706;</i><sub><i>x</i></sub><i>u</i>=0<br/>on the half line (-∞, 0] with decaying initial value. Assuming that the solution <i>u</i>(<i>x, t</i>) exists, we show that it can be represented in terms of the solution of a matrix Riemann-Hilbert problem formulated in the plane of the complex spectral parameter λ. The jump matrix has explicit (<i>x, t</i>) dependence and is given in terms of the spectral functions {<i>a</i>(λ), <i>b</i>(λ)} and {<i>A</i>(λ), <i>B</i>(λ)}, which are obtained from the initial data <i>u</i><sub>0</sub>(<i>x</i>)=<i>u</i>(<i>x</i>, 0) and the boundary data <i>g</i><sub>0</sub>(<i>t</i>)=<i>u</i>(0, <i>t</i>), <i>g</i><sub>1</sub>(<i>t</i>)=<i>u</i><sub><i>x</i></sub>(0, <i>t</i>), respectively. The spectral functions are not independent, but satisfy a so-called global relation.

Xu S W, He J S.

The rogue wave and breather solution of the Gerdjikov-Ivanov equation

J Math Phys, 2012, 53: 063507

[本文引用: 1]

Li X Y, Han G F, Zhao Q L.

Interactions of localized wave and dynamics analysis in generalized derivative nonlinear Schr¨odinger equation

Commun Nonlinear Sci, 2022, 114: 106612

[本文引用: 2]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发