推广的导数非线性薛定谔方程的单/双周期背景上的呼吸子和怪波及其碰撞解

摘要/Abstract

摘要：

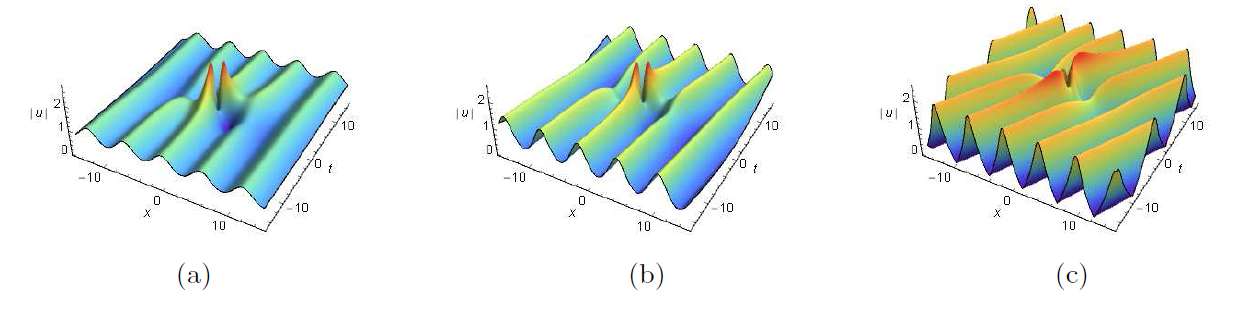
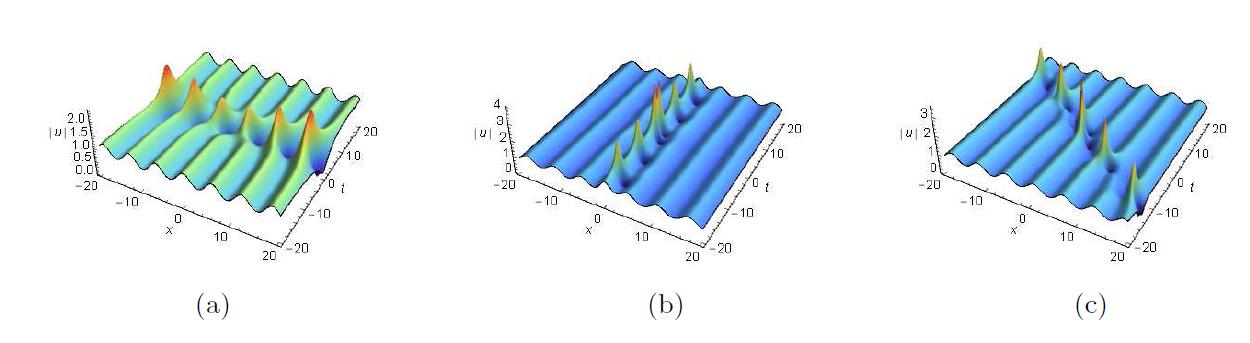
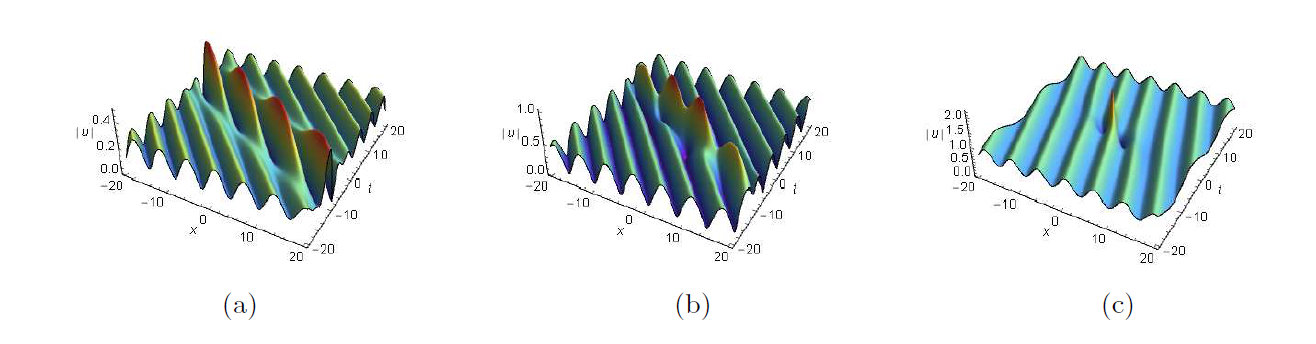
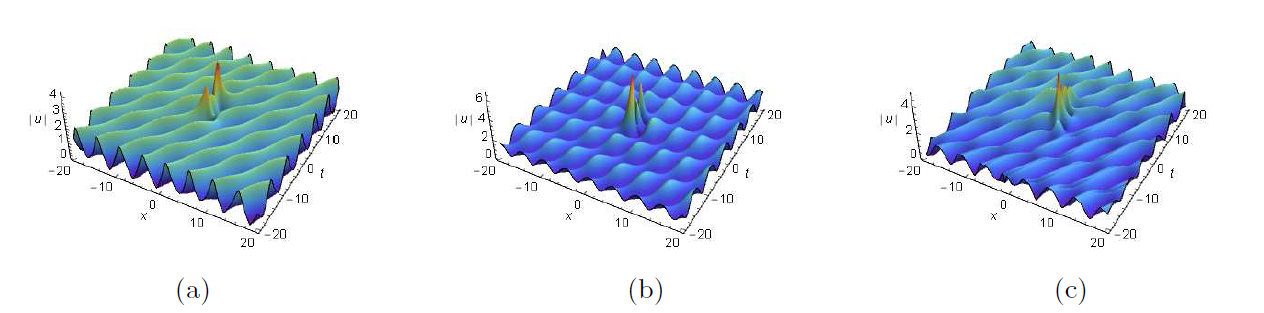
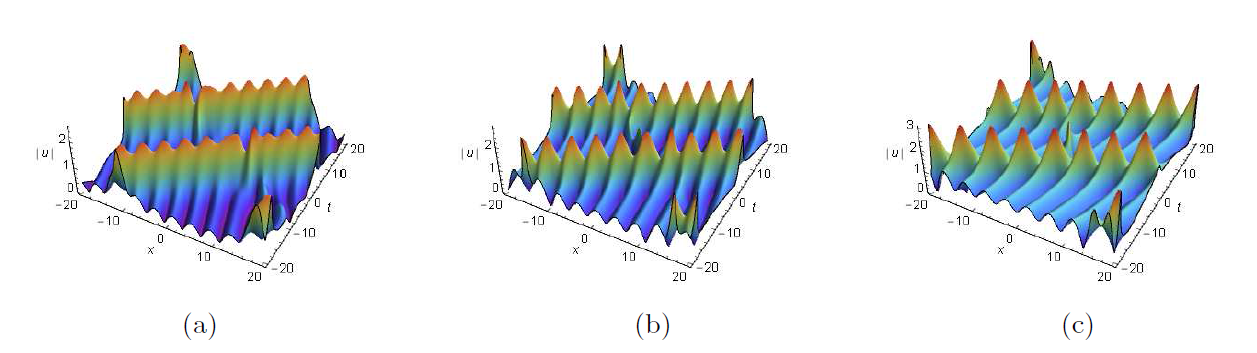
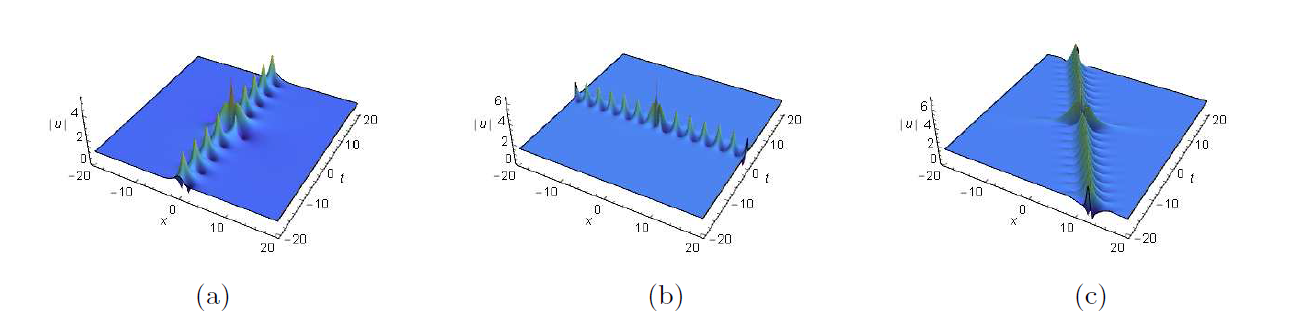
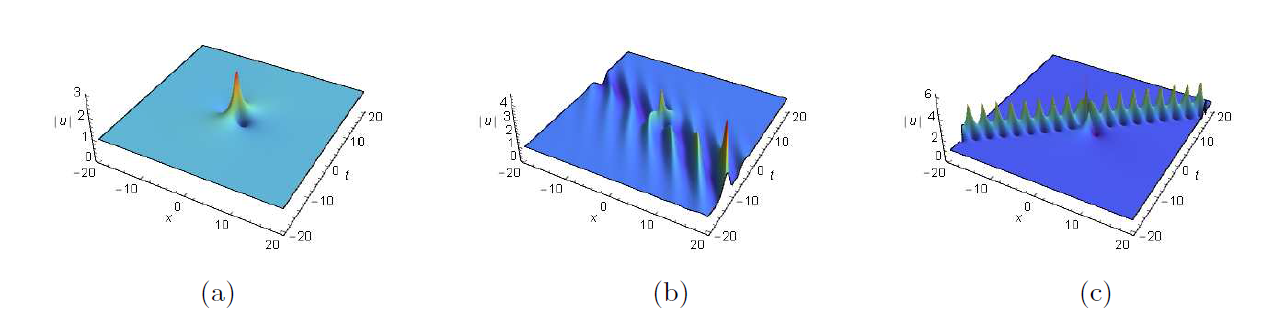
非线性薛定谔方程是物理和应用数学领域中一个非常重要的可积系统. 该文利用达布变换研究了推广的导数非线性薛定谔方程的单/双周期背景上的呼吸子和怪波以及呼吸子和怪波的碰撞解. 首先, 构造推广的导数非线性薛定谔方程的达布变换. 然后, 通过达布变换, 推导出周期背景和双周期背景上的呼吸子解和怪波解以及碰撞解. 最后, 借助于图示, 详细分析了有趣的新解结构. 这也为研究新型解的物理机制提供了理论依据.

关键词: 推广的导数非线性薛定谔方程, 达布变换, 周期解, 呼吸子, 怪波

Abstract:

The nonlinear Schr $\rm\ddot{o}$ dinger equation is a very important integrable system in the field of physics and applied mathematics. In this paper, the breather and rogue wave on the periodic/double periodic background and the collision solutions of breather and rogue wave for the generalized derivative nonlinear Schr $\rm\ddot{o}$ dinger equation are studied by using the Darboux transformation. Firstly, the Darboux transformation of the generalized derivative nonlinear Schr $\rm\ddot{o}$ dinger equation is constructed. Then, by using the Darboux transformation, the breather and rogue wave on the periodic/double periodic background and the collision solutions are derived. Finally, by means of the figures, the structures of interesting new solutions are analyzed in detail, which also provide a theoretical basis for studying the physical mechanism of the new solution.

Key words: The generalized derivative nonlinear Schr?dinger equation, Darboux transformation, Periodic solution, Breather, Rogue wave

中图分类号:

0175.24

娄瑜, 张翼. 推广的导数非线性薛定谔方程的单/双周期背景上的呼吸子和怪波及其碰撞解[J]. 数学物理学报, 2024, 44(6): 1511-1519.

Lou Yu, Zhang Yi. Breather and Rogue Wave on the Periodic/Double Periodic Background and Interaction Solutions of the Generalized Derivative Nonlinear Schr $\rm\ddot{o}$ dinger Equation[J]. Acta mathematica scientia,Series A, 2024, 44(6): 1511-1519.

图/表 7

图1

周期背景上的怪波解, 参数为 $a=1,c=1,\alpha=0,\beta=1,\alpha_3=0,$ (a) $\beta_3=\frac{1}{10};$ (b) $\beta_3=\frac{3}{10};$ (c) $\beta_3=\frac{3}{5}.$ "

图1

图2

周期背景上的呼吸子解, 参数为 $a=1,c=1,\alpha=0,\beta=1,$ (a) $\alpha_3=\frac{3}{10},\beta_3=\frac{3}{10};$ (b) $\alpha_3=\frac{11}{20},\beta_3=\frac{11}{20};$ (c) $\alpha_3=\frac{11}{20},\beta_3=\frac{9}{20}.$ "

图2

图3

周期背景上的呼吸子解, 参数为 $a=1,\alpha=0,\beta=1,\alpha_3=0,\beta_3=\frac{1}{10},$ (a) $c=\frac{1}{10};$ (b) $c=\frac{2}{5};$ (c) $c=\frac{4}{5}.$ "

图3

图4

双周期背景上的怪波解, 参数为 $a=1,c=1,\alpha=0,\beta=1,\alpha_3=0,\alpha_4=0,\beta_4=-\frac{3}{5},$ (a) $\beta_3=\frac{1}{10};$ (b) $\beta_3=\frac{1}{2};$ (c) $\beta_3=\frac{1}{5}.$ "

图4

图5

双周期背景上的怪波解, 参数为 $a=1,\alpha=0,\beta=1,\alpha_3=0,\alpha_4=0,\beta_3=\frac{3}{5},\beta_4=-\frac{1}{2},$ (a) $c=\frac{1}{5};$ (b) $c=\frac{1}{2};$ (c) $c=\frac{4}{5}.$ "

图5

图6

呼吸子和怪波的碰撞解, 参数为 $\alpha=0,\beta=1,$ (a) $a=1,c=1,\alpha_3=\frac{3}{5},\beta_3=-\frac{3}{5};$ (b) $a=\frac{9}{4},c=\frac{3}{2},\alpha_3=\frac{1}{2},\beta_3=-\frac{1}{2};$ (c) $a=\frac{8}{5},c=\frac{8}{5},\alpha_3=\frac{1}{2},\beta_3=-\frac{3}{5}.$ "

图6

图7

呼吸子和怪波的碰撞解, 参数为 $a=1,c=1,\alpha=0,\beta=1,\alpha_3=\frac{3}{5},$ (a) $\beta_3=0;$ (b) $\beta_3=-\frac{1}{10};$ (c) $\beta_3=-\frac{1}{5}.$ "

图7

参考文献 29

[1]	Olver P J, Sattinger D H. Solitons in Physics, Mathematics, and Nonlinear Optics. New York: Springer, 1990
[2]	Burger S, Bongs K, Dettmer S, Ertmer W, Sengstock K. Dark solitons in Bose-Einstein condenstates. Phys Rev Lett, 1999, 83: 5198-5201
[3]	Bludov Y V, Konotop V V, Akhmediev N. Matter rogue waves. Phys Rev A, 2009, 80: 033610
[4]	Yang B, Chen Y. Dynamics of high-order solitons in the nonlocal nonlinear Schr $\rm\ddot{o}$ dinger equations. Nonlinear Dynam, 2018, 94: 489-502
[5]	Ma W X. Riemann-Hilbert problems of a six-component mKdV system and its soliton solutions. Acta Math Sci, 2019, 29(2): 509-523
[6]	Akhmediev N, Korbeev V I. Modulation instability and periodic soulutions of the nonlinear Schr $\rm\ddot{o}$ dinger equation. Theoret Math Phys, 1986, 69: 1089-1093
[7]	Kuznetsov E A. Solitons in a parametrically unstable plasma. Dokl Akad Nauk SSSR, 1977, 236: 575-577
[8]	Priya N V, Senthilvelan M, Lakshmanan M. Akhmediev breathers, Ma solitons and general breathers from rogue waves: A case study in the Manakov system. Phys Rev E, 2013, 88(2): 022918
[9]	Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Phys Lett A, 2009, 373: 675-678
[10]	Wu X H, Gao Y T, Yu X, et al. Binary Darboux transformation, solitons, periodic waves and modulation instability for a nonlocal Lakshmana-Porsezian-Daniel equation. Wave Motion, 2022, 114: 103036
[11]	Zhai Y Y, Ji T, Geng X G. Coupled derivative nonlinear Schr $\rm\ddot{o}$ dinger III equation: Darboux transformation and higher-order rogue waves in a two-mode nonlinear fiber. Appl Math Comput, 2021, 411: 126551
[12]	L $\rm\ddot{u}$ Xing, Chen S J. Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: one-lump-multi-stripe and one-lump-multi-soliton types. Nonlinear Dynam, 2021, 103: 947-977
[13]	房春梅, 田守富. 约化的(3+1)维 Hirota 方程的呼吸波解、Lump 解和半有理解. 数学物理学报, 2022, 42A(3): 775-783
	Fang C M, Tian S F. Breather Wave Solutions, Lump solutions and semi-rational solutions of a reduced (3+1) dimensional Hirota equation. Acta Math Sci, 2022, 42A(3): 775-783
[14]	Ma W X. Bilinear equations and resonant solutions characterized by Bell polynomials. Rep Math Phys, 2013, 72(1): 41-56
[15]	Ma W X. Trilinear equations, Bell polynomials, and resonant solutions. Front Math China, 2013, 8: 1139-1156
[16]	田守富. 一个广义导数非线性 Schr $\rm\ddot{o}$ dinger 方程的 Riemann-Hilbert 问题: 长时间渐近行为. 中国科学: 数学, 2022, 52(5): 505-542
	Tian S F. Riemann-Hilbert problem to a generalized derivative nonlinear Schr $\rm\ddot{o}$ dinger equation: Long-time asymptotic behavior. Sci Sin Math, 2022, 52(5): 505-542
[17]	Wei H Y, Fan E G, Guo H D. Riemann-Hilbert approach and nonlinear dynamics of the coupled higher-order nonlinear Schr $\rm\ddot{o}$ dinger equation in the birefringent or two-mode fiber. Nonlinear Dynam, 2021, 104: 649-660
[18]	Chen X T, Zhang Y, Ye R S. Riemann-Hilbert approach of the coupled nonisospectral Gross-Pitaevskii system and its multi-component generalization. Appl Anal, 2019, 100(10): 2200-2209
[19]	Hu B B, Xia T C, Ma W X. Riemann-Hilbert approach for an initial-boundary value problem of the two-component modified Korteweg-de Vries equation on the half-line. Appl Math Comput, 2018, 332: 148-159
[20]	Guo B L, Ling L M, Liu Q P, Wu C F. Nonlinear Schr $\rm\ddot{o}$ dinger equation: generalized Darboux transformation and rogue wave solutions. Phys Rev E, 2012, 85: 026607
[21]	Wang X, Wei J. Three types of Darboux transformation and general soliton soulutions for the space-shifted nonlocal PT symmetric nonlinear Schr $\rm\ddot{o}$ dinger equation. Appl Math Lett, 2022, 130: 107998
[22]	Zhang Y, Ye R S, Ma W X. Binary Darboux transformation and soliton solutions for the coupled complex modified Korteweg-de Vries equations. Math Meth Appl Sci, 2019, 43: 613-627
[23]	Fan E G. Integrable evolution systems based on Gerdjikov-Ivanovequations, bi-Hamiltonian structure, finite-dimensional integrable systems and $N$ -fold Darboux transforamtion. J Math Phys, 2000, 41: 7769-7782
[24]	Shen Y, Tian B, Zhou T Y, Gao X T. $N$ -fold Darboux transformation and solitonic interactions for the Kraenkel-Manna-Merle system in a saturated ferromagnetic material. Nonlinear Dynam, 2023, 111: 2641-2649
[25]	Kodama Y J. Optical solitons in a monomode fiber. J Stat Phys, 1985, 39: 597
[26]	Chen J B, Pelinovsky D E, Upsal J. Modulation instability of periodic standing waves in the derivative NLS equation. J Nonlinear Sci, 2021, 31: 58
[27]	Zhang N, Xia T C, Fan E G. A Riemann-Hilbert approach to the Chen-Lee-Liu equation on the half line. Acta Math Appl Sin-E, 2018, 34: 493-515 doi: 10.1007/s10255-018-0765-7
[28]	Xu S W, He J S. The rogue wave and breather solution of the Gerdjikov-Ivanov equation. J Math Phys, 2012, 53: 063507
[29]	Li X Y, Han G F, Zhao Q L. Interactions of localized wave and dynamics analysis in generalized derivative nonlinear Schr $\rm\ddot{o}$ dinger equation. Commun Nonlinear Sci, 2022, 114: 106612

Metrics

Viewed

Full text

125

HTML			PDF

Just accepted	Online first	Issue	Just accepted	Online first	Issue
0	0	0	0	0	125

	From	local

	Times	125
	Rate	100%

Abstract

Just accepted	Online first	Issue

0	0	51

From	Others	local

Times	47	4
Rate	92%	8%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed