数学物理学报, 2024, 44(6): 1499-1510

带间断系数的奇异摄动对流扩散方程的 NIPG 有限元方法

徐磊,, 刘利斌,*

南宁师范大学 广西应用数学中心 南宁 530100

Uniformly Convergent NIPG Methods for a Singularly Perturbed Convection-Diffusion Problem with a Discontinuous Convection Coefficient

Xu Lei,, Liu Libin,*

Center for Applied Mathematics of Guangxi, Nanning Normal University, Nanning 530100

通讯作者: *刘利斌, Email：liulibin969@163.com

收稿日期: 2023-01-15   修回日期: 2024-04-17  

基金资助: 国家自然科学基金(12361087)
广西科技基地和人才专项(AD23023003)
广西研究生教育创新计划资助(YCSW2023438)

Received: 2023-01-15   Revised: 2024-04-17  

Fund supported: National Science Foundation of China(12361087)
Guangxi Science and Techology Program(AD23023003)
Innovation Project of Guangxi Graduate Education(YCSW2023438)

作者简介 About authors

徐磊,Email：xulei19980919@163.com

摘要

针对带间断系数的奇异摄动对流扩散方程, 该文在 Bakhvalov-type 网格下, 构造了一种 NIPG 高阶有限元方法. 基于 Gauß Radau 投影和 Lagrange 插值, 推导出 NIPG 方法的最优一致收敛性.最后的数值实验支持了作者的理论结果.

关键词： 奇异摄动; 间断系数; NIPG 方法; Bakhvalov-type 网格

Abstract

In this paper, a higher order NIPG method on a Bakhvalov-type mesh for a singularly perturbed convection-diffusion problem with a discontinuous convection coefficient is studied. Based on Gauß Radau interpolation and Lagrange interpolation, the convergence of optimal order in an energy norm is derived. Numerical experiments are proposed to confirm our theoretical results.

Keywords： Singularly perturbed; Nonsmooth coefficient; NIPG method; Bakhvalov-type mesh

PDF (586KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

徐磊, 刘利斌. 带间断系数的奇异摄动对流扩散方程的 NIPG 有限元方法[J]. 数学物理学报, 2024, 44(6): 1499-1510

Xu Lei, Liu Libin. Uniformly Convergent NIPG Methods for a Singularly Perturbed Convection-Diffusion Problem with a Discontinuous Convection Coefficient[J]. Acta Mathematica Scientia, 2024, 44(6): 1499-1510

1 引言

本文考虑如下带间断系数的奇异摄动对流扩散方程

$\begin{equation} \begin{aligned} &Lu:=-\varepsilon u''+b(x)u'(x)+c(x)u(x)=f(x),x\in \Omega^{-}\cup \Omega^{+},\\ &u(0)=0,u(1)=0, \end{aligned} \end{equation}$

其中 $0<\varepsilon\ll 1$ 是摄动参数, $\Omega^{-}=(0,d)$, $\Omega^{+}=(d,1)$, $b,c,f\in C^{2k}(\Omega^{-}\cup \Omega^{+})$, 且对于给定的常数 $\gamma$, 满足

$c(x)-\frac{1}{2} b^{\prime}(x) \geq \gamma^{2}>0, x \in \Omega^{-} \cup \Omega^{+}.$

此外, 假设存在与 $\varepsilon$ 无关的常数 $\beta_1,\beta_{1}^{ \star},\beta_2,\beta_{2}^{ \star}$, $C$, 使得

$\begin{equation} \begin{aligned} &\beta_{1}^{ \star} > b(x) >\beta_{1}>0,x<d, -\beta_{2}^{ \star}<b(x)<-\beta_{2}<0,x>d, c(x)\geq 0, x\in \bar{\Omega},\\ &\left|[b](d) \right|\leq C, \left|[c](d) \right|\leq C, \left|[f](d) \right|\leq C. \end{aligned} \end{equation}$

在这里, 对于任意函数 $w(x)$, 定义 $[w(d)]=w(d^{+})-w(d^{-})$.方程 (1.1) 的解 $u(x)$ 通常在不连续点 $x=d$ 处产生一个宽度为 $O(\varepsilon \ln(1/\varepsilon))$ 的内点层[1].

具有非光滑系数的奇异摄动微分方程在流体力学, 量子力学, 弹性力学, 气体多孔电极理论, 气象学, 海洋学等领域有着广泛的应用. 这类问题的一个显著特点是高阶导数项包含一个摄动参数 $\varepsilon$, 且对流项和右边源项在区域内部存在间断点. 当 $\varepsilon\to 0$ 时, 这类问题的解在区域的边界和内部某个区域内会产生剧烈的振荡, 即存在所谓的边界层和内点层现象[2]. 正因为边界层或内点层的出现, 在很多情况下很难给出这类问题的精确解.

因此, 目前常用的数值方法是在层适应网格 (Shishkin 网格和 Bakhvalov 网格) 下构造出相应的迎风有限差分格式, 并证明离散格式的一致收敛性[3,4]. 然而, 据我们所知, 这类方法的收敛性一般只有一阶或者二阶精度.

与有限差分方法相比, 有限元方法更方便处理复杂区域, 且易构造更高阶格式. 因此, 少数学者研究了带间断系数的奇异摄动对流扩散方程的有限元方法. 例如,Zarin 等[5]在 Shishkin 网格下构造了带间断系数的奇异摄动对流扩散方程的标准有限元方法, 并在能量范数下证明了数值格式是几乎一阶一致收敛的. 在此基础上, 张进等[1] 给出了能量范数下几乎 $k$ 阶一致收敛的证明. Babu 等[6]在 Shishkin 网格下使用流线扩散有限元方法证明了数值格式在最大范数下是几乎二阶收敛的. 据我们查阅相关资料发现, 在 Bakhvalov 网格下, 目前还没有相关文献报道问题 (1.1) 的高阶有限元方法, 其困难主要源于标准的 Lagrange 插值不适用于 Bakhvalov 网格下有限元方法的一致收敛分析. 更具体地说, Lagrange 插值不能在网格过渡点附近提供足够的 $L^2$ 范数稳定性, 所以有限元方法在 Bakhvalov 网格上的研究进展缓慢.

Linß 等[7]指出, 虽然 Galerkin 有限元在层适应网格上能获得一致收敛的结果, 但是数值结果对层适应网格中参数的选择较敏感, 所以仍然有必要在层适应网格上使用稳定性较强的数值方法.自 1970 年以来, 非对称内惩罚伽辽金 (NIPG) 方法逐渐成为一种流行的稳定技术. 由于该方法采用了内部惩罚项来约束单元边界的不连续, 因此它具有协调有限元所没有的灵活性和优点. 此外, 与 DG 方法的其他变体—例如对称内罚伽辽金方法和不完全内罚伽辽金方法相比, 该方法对任何非负惩罚参数和任何网格都具有稳定性和收敛性. 鉴于其自身独特的优势, NIPG 方法引起了越来越多研究者的关注[8⇓⇓-11].

基于此, 本文针对带间断系数的奇异摄动对流扩散方程 (1.1), 构造了一种 Bakhvalov-type 网格. 通过设计一种新的复合型插值方法, 它由层外的 Gauß Radau 投影和层内的 Lagrange 插值组成, 从而推导出 Bakhvalov-type 网格下 NIPG 方法的最优一致收敛性. 最后的数值实验支持了我们的理论结果.

假设 1.1 我们将在整篇文章中假设 $\varepsilon \leq CN^{-1}$, 这在实践中并不是一种限制.

2 预备知识

为了后续误差分析的需要, 在这部分给出连续解的存在性、稳定性及导数估计, 见如下引理 2.1-2.3

引理 2.1[1] 若 $u(x)$ 是问题 (1.1) 的解, 则 $u(x)\in C^{0}(\bar{\Omega})\cap C^{1}(\Omega)\cap C^{2}(\Omega^{-}\cup \Omega^{+})$.

引理 2.2[1] 若问题 (1.1) 的解 $u(x)\in C^{0}(\bar{\Omega})\cap C^{1}(\Omega)\cap C^{2}(\Omega^{-}\cup \Omega^{+})$, 则

$\begin{eqnarray*} \left\| u(x) \right\|_{\infty} \leq \frac{1}{\lambda} \left\| f(x) \right\|_{\infty}, \end{eqnarray*}$

其中 $\lambda=\min\{\beta_1/d,\beta_2/(1-d)\}$.

引理 2.3[1] 假设问题 (1.1) 的解可分解为 $u=S+E$, 其中光滑部分 $S$ 和层部分 $E$ 分别满足 $LS=f$ 和 $LE=0$. 那么对于任意 $0\leq i \leq k+1$, 有

$\begin{equation} \begin{aligned} &\left\|S^{(i)}(x)\right\|_{\infty,\Omega^{-}\cup \Omega^{+}} \leq C, \left|[S](d) \right|\leq C, \left|[S'](d) \right|\leq C,\\ &\left|E^{(i)}(x) \right|\leq \begin{cases} C\varepsilon^{-i}{\rm e}^{(x-d)\beta_{1}/\varepsilon}, &x\in \Omega^{-},\\ C\varepsilon^{-i}{\rm e}^{-(x-d)\beta_{2}/\varepsilon}, &x\in \Omega^{+}. \end{cases} \end{aligned} \end{equation}$

3 NIPG 高阶有限元方法的构造

3.1 Bakhvalov-type 网格

由引理 2.3 可知, 问题 (1.1) 的解在 $x = d$ 处存在内点层. 因此, 为了构造出有效的 Bakhvalov-type 网格, 我们首先将 $\bar{\Omega}$ 分为四个子区间

$\begin{eqnarray*} \bar{\Omega}=[\tau_1]\cup [\tau_1,d]\cup [d,\tau_2]\cup [\tau_2,1], \end{eqnarray*}$

其中 $\tau_1=d+\frac{\sigma \varepsilon }{\beta_1}\ln \varepsilon$, $\tau_2=d-\frac{\sigma \varepsilon}{\beta_2}\ln \varepsilon$, 且满足 $d-\tau_1\leq d/2$ 和$\tau_2-d\leq (1-d)/2$.假设 $N\in \mathbb{N},N\geq 16$ 是一个能被 4 整除的整数并且 $\sigma\geq k+1$.我们将上述四个子区间分别分成 $N/4$ 个小区间, 则每一个网格节点 $x_j$ 可以表示为

$\begin{equation} x_{j}= \begin{cases} 4 \tau_1\frac{j}{N}, & j=0,1,\cdots,\frac{N}{4},\\[3mm] d+ \frac{\sigma \varepsilon}{\beta_1} \ln \left[1+4\left(1-\varepsilon\right)\left(\frac{j}{N}-\frac{1}{2}\right)\right], & j= \frac{N}{4},\frac{N}{4}+1,\cdots,\frac{N}{2},\\[3mm] d- \frac{\sigma \varepsilon}{\beta_2} \ln \left[1-4\left(1-\varepsilon\right)(\frac{j}{N}-\frac{1}{2})\right], & j=\frac{N}{2},\frac{N}{2}+1,\cdots,\frac{3N}{4},\\[3mm] \tau_2+4(1-\tau_2)(\frac{j}{N}-\frac{3}{4}), & j=\frac{3N}{4},\frac{3N}{4}+1,\cdots,N. \end{cases} \end{equation}$

Bakhvalov-type 网格具有如下性质

引理 3.1 令 $h_{j}=x_{j}-x_{j-1}$, 则有

$C_{1}N^{-1}\leq h_{j} \leq C_{2}N^{-1}, 1 \leq j \leq \frac{N}{4},$
$C\varepsilon \leq h_{\frac{N}{4}+1} \leq CN^{-1}, C_{3}\varepsilon \leq h_{\frac{N}{4}+2} \leq C_{4}\varepsilon,$
$h_{\frac{N}{4}+2}\geq h_{\frac{N}{4}+3} \geq \cdots \geq h_{\frac{N}{2}},$
$h_{\frac{N}{2}+1}\leq h_{\frac{N}{2}+2} \leq \cdots \leq h_{\frac{3N}{4}-1},$
$C_{5}\varepsilon \leq h_{\frac{3N}{4}-1} \leq C_{6}\varepsilon,C\varepsilon \leq h_{\frac{3N}{4}} \leq CN^{-1},$
$C_{7}N^{-1}\leq h_{j} \leq C_{8}N^{-1}, \frac{3N}{4}+1 \leq j \leq N.$

进一步, 对于 $0 \leq \nu \leq \sigma$, 有

$\begin{aligned}&h_{j}^{\nu}{\rm e}^{(x_{j}-d)\beta_{1}/\varepsilon} \leq C\varepsilon^{\nu}N^{-\nu}, \frac{N}{4}+2 \leq j\leq \frac{N}{2}, \end{aligned}$
$\begin{aligned}&h_{j}^{\nu}{\rm e}^{-(x_{j-1}-d)\beta_{2}/\varepsilon} \leq C\varepsilon^{\nu}N^{-\nu}, \frac{N}{2}+1 \leq j\leq \frac{3N}{4}-1. \end{aligned}$

证 证明见文献 [12,引理 3].

3.2 NIPG 方法及其性质

令 $\mathcal{T}_{N}=\{ I_{j}=[x_{j-1},x_{j}]:j=1,\cdots,N \}$ 为区域 $\Omega$ 的一个网格剖分, 则对任意单元 $I_{j}\in \mathcal{T}_{N}$, 定义 $s$ 阶的分片 Sobolev 空间

$\begin{equation*} H^{s}(\Omega,\mathcal{T}_{N})=\{ u\in L^{2}(\Omega) : u|_{I_{j}} \in H^{s}(I_{j}), \forall j=1,2,\cdots,N \} \end{equation*}$

和相应的分片 Sobolev 范数和半范数

$\begin{equation*} \left\|u\right\|_{s,\mathcal{T}_{N}}^{2}=\sum_{j=1}^{N} \left\|u\right\|_{s,I_{j}}^{2}, |u|_{s,\mathcal{T}_{N}}^{2}=\sum_{j=1}^{N} |u|_{s,I_{j}}^{2}, \end{equation*}$

其中 $\left\|\cdot\right\|_{s,I_{j}}$ 和 $\left|\cdot\right| _{s,I_{j}}$ 是 $H^{s}(I_{j})$ 中常见的 Sobolev 范数和半范数. 在这里, $\left\|\cdot\right\|_{I}$ 和 $(\cdot,\cdot)_{I}$ 分别表示 $L^{2}(I)$ 范数和 $L^{2}(I)$ 内积.

为了构造出问题 (1.1) 的 NIPG 有限元方法, 在 Bakhvalov-type 网格下, 定义如下有限元空间

$\begin{equation*} V_{N}^{k}=\{ u \in L^{2}(\Omega) : u|_{I_{j}} \in \mathbb{P}_{k}(I_{j}), \forall j=1,2,\cdots,N \}, \end{equation*}$

其中 $\mathbb{P}_{k}(I_{j})$ 是 $I_{j}$ 上次数不超过 $k$ 次的多项式空间. $V_{N}^{k}$ 空间中的函数在单元边界处是完全间断的.

对于给定的函数 $u(x)\in V_{N}^{k}$, 令$u(x_{j}^{+})$ 和 $u(x_{j}^{-})$ 分别表示 $u$ 在 $x_{j}$ 的右侧和左侧取值, 则函数 $u$ 在内部节点 $x_{j}$ 处的跳跃和平均为

$\begin{equation*} [u(x_{j})]=u(x_{j}^{+})-u(x_{j}^{-}), \{u(x_{j})\}=\frac{1}{2}\left(u(x_{j}^{+})+u(x_{j}^{-})\right), \forall j=1,\cdots,N-1. \end{equation*}$

为表述方便, 我们将边界节点 $x_{0}$ 和 $x_{N}$ 处的跳跃和平均定义为

$\begin{equation*} [u(x_{0})]=u(x_{0}^{+}), \{u(x_{0})\}=u(x_{0}^{+}), [u(x_{N})]=-u(x_{N}^{-}), \{u(x_{N})\}=u(x_{N}^{-}). \end{equation*}$

基于以上的定义, 我们给出问题 (1.1) 的 NIPG 有限元离散格式: 寻找 $u_{N}\in V_{N}^{k}$ 使得

$\begin{equation} a(u_{N},v_{N})=a_{1}(u_N,v_N)+a_{2}(u_N,v_N)=L(v_{N}), \forall v_{N} \in V_{N}^{k}, \end{equation}$

其中, 对任意 $u,v \in H^{1}(\Omega,\mathcal{T}_{N})$, 算子 $a_j(\cdot,\cdot)(j=1,2)$, $L(\cdot)$ 的定义如下

$\begin{equation*} \begin{aligned} &a_{1}(u,v)=\sum_{j=1}^{N} \int_{I_{j}} \varepsilon u' v'{\rm d}x +\sum_{j=0}^{N} \varepsilon \left(\{u'(x_{j})\}[v(x_{j})]-\{v'(x_{j})\}[u(x_{j})] \right) +\sum_{j=0}^{N} \lambda_{j} [u(x_{j})] [v(x_{j})],\\ &a_{2}(u,v)=\sum_{j=1}^{N} \int_{I_{j}} ( bu'+cu)v{\rm d}x +\sum_{j=0}^{N-1} b(x_{j}) [u(x_{j})] v(x_{j}^{+}),\\ &L(v)=\sum_{j=1}^{N} \int_{I_{j}} fv{\rm d}x. \end{aligned} \end{equation*}$

这里 $\lambda_{j}(j=0,\cdots,N)$ 是与节点 $x_{j}$ 相关的非负惩罚参数, 本文取 $\lambda_{j}=N, j=0,\cdots,N$.

引理 3.2 若 $u$ 和 $u_{N}$ 分别是问题 (1.1) 和 (3.10) 的精确解, 则双线性形式 $a(\cdot,\cdot)$ 满足如下 Galerkin 正交性

$\begin{equation} a(u-u_{N},v)=0, \forall v \in V_{N}^{k}. \end{equation}$

证 类似于文献 [11,引理 2.2].

为了讨论双线性形式 $a(\cdot,\cdot)$ 的稳定性, 我们定义如下能量范数

$\begin{equation} \left\|v\right\|_{\varepsilon}^{2} =\sum_{j=1}^{N} \left(\varepsilon \left\|v'\right\|_{I_{j}}^{2} +\left\| \gamma v\right\|_{I_{j}}^{2} \right) +\sum_{j=0}^{N} \left(\frac{1}{2} b(x_{j})+ \lambda_{j} \right) [v(x_{j})]^{2}, \forall v \in V_{N}^{k}. \end{equation}$

通过简单计算, 我们可以得到

$\begin{equation} \left\|v_{N}\right\|_{\varepsilon}^{2}\leq a(v_N,v_N), \forall v_N \in V_{N}^{k}. \end{equation}$

基于 Lax-Milgram 引理, 问题 (3.10) 存在唯一解 $u_N$.

4 插值及误差估计

引入 $u$ 的一个复合型插值 $\Pi u$, 即

$\begin{equation} (\Pi u)|_{I_{j}}= \begin{cases} (L_{k}u)|_{I_{j}}, & \text{如果} \frac{N}{4}+2 \leq j \leq \frac{3N}{4}-1, \\[3mm] (P_{h}u)|_{I_{j}}, & \text{如果} 1 \leq j \leq \frac{N}{4}+1, \frac{3N}{4} \leq j \leq N, \end{cases} \end{equation}$

其中 $L_{k}u$ 是 $u$ 的 $k$ 次 Lagrange 插值, 而 $P_{h}u$ 是 $u$ 的 Gauß Radau 投影. 同时给出 Gauß Radau 投影 $(P_{h}w)|_{I_{j}}$ 的定义[13]: 对于 $j=1,2,\cdots,N$,

$\begin{aligned}&\int_{I_{j}} (P_{h}w)v{\rm d}x= \int_{I_{j}} wv{\rm d}x, \forall v\in \mathbb{P}_{k-1}(I_{j}), \end{aligned}$
$\begin{aligned}&(P_{h}w)(x_{j}^{-})=w(x_{j}^{-}). \end{aligned}$

根据文献 [13] 中的投影结果, 对所有 $w\in H^{k+1}(I_j),j=1,2,\cdots,N$, 有

$\begin{aligned}&\left\|w-P_{h}w \right\|_{I_j} +h_{j}^{\frac{1}{2}} \left\|w-P_{h}w \right\|_{L^{\infty}(I_j)} \leq C h_{j}^{k+1} \left| w \right|_{k+1,I_{j}}, \end{aligned}$
$\begin{aligned}&\left\|P_{h}w \right\|_{L^{\infty}(I_j)} \leq C\left\|w \right\|_{L^{\infty}(I_j)}. \end{aligned}$

由 Lagrange 插值算子的定义以及 Sobolev 空间中的插值理论[14], 对所有 $w\in W^{k+1,p}(I_{j}),$$j=1,2,\cdots,N$, 有

$\left\|w-L_{k} w\right\|_{W^{l, q}\left(I_{j}\right)} \leq C h_{j}^{k+1-l+1 / q-1 / p}|w|_{W^{k+1, p}\left(I_{j}\right)},$

其中 $l=0,1$ 且 $1\leq p,q \leq \infty$.

引理 4.1 假设 $\sigma \geq k+1$, 在 Bakhvalov-type 网格上有

$\begin{aligned}& \left\|u-\Pi u \right\|_{L^{\infty}(I_j)} \leq CN^{-(k+1)}, j=1,2,\cdots,N, \end{aligned}$
$\begin{aligned}& \left\|(E-P_{h}E)' \right\|_{[x_{\frac{N}{4}+1}]} \leq C\varepsilon^{\sigma}N+C\varepsilon^{-\frac{1}{2}}N^{-\sigma}, \end{aligned}$
$\begin{aligned} &\left\|u-P_{h}u \right\|_{\varepsilon,[x_{\frac{N}{4}+1}]} \leq CN^{-k},\end{aligned}$
$\begin{aligned} &\left\|u-L_{k}u \right\|_{\varepsilon,[x_{\frac{N}{4}+1},d]} \leq CN^{-k}. \end{aligned}$

证 利用文献 [15,引理 2] 以及 (4.4) 和 (4.6) 式可得出该引理.

情况1 通过使用引理 4.1 中的方法, 我们可以很容易地在 $[d,1]$ 上得到类似的结果, 即

$\begin{eqnarray*} &&\left\|(E-P_{h}E)' \right\|_{[x_{\frac{3N}{4}-1},1]} \leq C\varepsilon^{\sigma}N+C\varepsilon^{-\frac{1}{2}}N^{-\sigma},\\ &&\left\|u-P_{h}u \right\|_{\varepsilon,[x_{\frac{3N}{4}-1},1]} \leq CN^{-k},\\ &&\left\|u-L_{k}u \right\|_{\varepsilon,[d,x_{\frac{3N}{4}-1}]} \leq CN^{-k}. \end{eqnarray*}$

引理 4.2[16] 令 $w\in H^{1}(I_j)$, 则

$\left|w\left(x_{s}\right)\right|^{2} \leq 2\left(h_{j}^{-1}\|w\|_{I_{j}}^{2}+\|w\|_{I_{j}}\left\|w^{\prime}\right\|_{I_{j}}\right), \quad s \in\{j-1, j\}.$

引理 4.3 令 $\eta=u-\Pi u$, 在 Bakhvalov-type 网格上有

$\begin{equation} \{\eta'(x_{j})\}^{2}\leq \begin{cases} C \varepsilon^{-2} N^{-2(k+1)}, & 0 \leq j \leq \frac{N}{4}, \frac{3N}{4} \leq j \leq N, \\[3mm] C \varepsilon^{-2} N^{-2k}, & \frac{N}{4}+1 \leq j \leq \frac{3N}{4}-1. \end{cases} \end{equation}$

证 类似地利用文献 [16,引理 3.6] 提出的方法, 可以很容易得到该引理.

由引理 4.1 和情况 1 可以推出下面插值误差的估计结果.

定理 4.1 令 $\sigma \geq k+1$, 那么在 Bakhvalov-type 网格上, 有

$\begin{equation} \left\| u-\Pi u \right\|_{\varepsilon} \leq CN^{-k}. \end{equation}$

5 一致收敛性分析

引入 $\xi=\Pi u-u_N$. 由 Galerkin 正交性, (3.13) 式和分部积分可得

$\begin{equation} \begin{aligned} \left\|\xi\right\|_{\varepsilon}^{2} &\leq a(\xi,\xi)=a(\Pi u-u+u-u_{N},\xi)=a(\eta,\xi)\\ &=\sum_{j=1}^{N} \int_{I_{j}} \varepsilon \eta' \xi'{\rm d}x +\sum_{j=0}^{N} \varepsilon \{\eta'(x_{j})\}[\xi(x_{j})] -\sum_{j=0}^{N} \varepsilon \{\xi'(x_{j})\}[\eta(x_{j})] \\ & +\sum_{j=0}^{N} \lambda_j [\eta(x_{j})] [\xi(x_{j})] +\sum_{j=1}^{N} \int_{I_{j}} (b\eta'+c\eta)\xi{\rm d}x +\sum_{j=0}^{N-1} b(x_{j}) [\eta(x_{j})] \xi(x_{j}^{+})\\ &=\sum_{j=1}^{N} \int_{I_{j}} \varepsilon \eta' \xi'{\rm d}x +\sum_{j=0}^{N} \varepsilon \{\eta'(x_{j})\}[\xi(x_{j})] -\sum_{j=0}^{N} \varepsilon \{\xi'(x_{j})\}[\eta(x_{j})] \\ & +\sum_{j=0}^{N} \lambda_j [\eta(x_{j})] [\xi(x_{j})] -\sum_{j=1}^{N} \int_{I_{j}} b\eta\xi'{\rm d}x -\sum_{j=1}^{N} b(x_{j}) [\xi(x_{j})] \eta(x_{j}^{-})\\ & +\sum_{j=1}^{N} \int_{I_{j}} (-b'+c)\eta\xi{\rm d}x\\ &=\Gamma_{1}+\Gamma_{2}+\Gamma_{3}+\Gamma_{4}+\Gamma_{5}+\Gamma_{6}+\Gamma_{7}. \end{aligned} \end{equation}$

接下来, 我们将分别分析 (5.1) 式右端的每一项 $\Gamma_i(i=1,\cdots,7)$.

首先, 利用 Hölder 不等式和 (4.13) 式可得

$\left|\Gamma_{1}\right| \leq\left(\sum_{j=1}^{N} \int_{I_{j}} \varepsilon\left(\eta^{\prime}\right)^{2} \mathrm{~d} x\right)^{\frac{1}{2}}\left(\sum_{j=1}^{N} \int_{I_{j}} \varepsilon\left(\xi^{\prime}\right)^{2} \mathrm{~d} x\right)^{\frac{1}{2}} \leq\|\eta\|_{\varepsilon}\|\xi\|_{\varepsilon} \leq C N^{-k}\|\xi\|_{\varepsilon}.$

对于 $\Gamma_2$, 根据 (4.12) 式和 $\lambda_j=N$, 可得

$\begin{equation} \begin{aligned} |\Gamma_2| &\leq \bigg(\sum_{j=0}^{N} \frac{\varepsilon^{2}}{\lambda_j}\{\eta'(x_{j})\}^{2}\bigg)^{\frac{1}{2}} \bigg(\sum_{j=0}^{N} \lambda_j [\xi(x_{j})]^{2}\bigg)^{\frac{1}{2}} \leq CN^{-k} \left\|\xi\right\|_{\varepsilon}. \end{aligned} \end{equation}$

为了估计 $\Gamma_3$, 我们首先将 $\Gamma_3$ 分解成

$\begin{equation*} \Gamma_3= - \varepsilon \sum_{j=0}^{\frac{N}{4}+1} \{\xi'(x_{j}) \} [\eta(x_{j})] - \varepsilon \sum_{j=\frac{N}{4}+2}^{\frac{3N}{4}-2} \{\xi'(x_{j}) \} [\eta(x_{j})] - \varepsilon \sum_{j=\frac{3N}{4}-1}^{N} \{\xi'(x_{j}) \} [\eta(x_{j})]. \end{equation*}$

根据 (4.1) 式和 Lagrange 插值的连续性质, 可知 $[\eta(x_j)]=0,j=\frac{N}{4}+2,\cdots,\frac{3N}{4}-2$. 同时, 利用逆不等式, (4.7), (3.2), (3.3) 式和 $\varepsilon\leq N^{-1}$, 可以得到

$\begin{equation*} \begin{aligned} & \left|-\varepsilon\sum_{j=0}^{\frac{N}{4}+1}[\eta(x_{j})] \{\xi'(x_{j})\}\right|\\ &\leq |\varepsilon[\eta(x_{0})] \{\xi'(x_{0})\}| +|\varepsilon\sum_{j=1}^{\frac{N}{4}+1}[\eta(x_{j})] \{\xi'(x_{j})\}|\\ &\leq C \varepsilon \left\| \eta\right\|_{L^{\infty}(I_{1})} \left\|\xi'\right\|_{L^{\infty}(I_1)} +C\varepsilon\sum_{j=1}^{\frac{N}{4}+1} \left\| \eta\right\|_{L^{\infty}(I_{j}\cup I_{j+1})} \left\|\xi'\right\|_{L^{\infty}(I_{j}\cup I_{j+1})}\\ &\leq C \varepsilon \left\| \eta\right\|_{L^{\infty}(I_{1})} N^{\frac{1}{2}} \left\|\xi'\right\|_{I_1} +C\varepsilon\sum_{j=1}^{\frac{N}{4}+1} \left\| \eta\right\|_{L^{\infty}(I_{j})} \max\{h_{j}^{-\frac{1}{2}},h_{j+1}^{-\frac{1}{2}}\} \left\|\xi'\right\|_{I_{j}\cup I_{j+1}}\\ &\leq C N^{-(k+1)} \left\|\xi\right\|_{\varepsilon} +C \bigg(\sum_{j=1}^{\frac{N}{4}+1} \left\| \eta\right\|_{L^{\infty}(I_{j})}^{2}\bigg)^{\frac{1}{2}} \bigg(\sum_{j=1}^{\frac{N}{4}+1}\varepsilon\left\|\xi'\right\|_{I_{j}\cup I_{j+1}}^{2}\bigg)^{\frac{1}{2}}\\ &\leq CN^{-(k+\frac{1}{2})} \left\|\xi \right\|_{\varepsilon}. \end{aligned} \end{equation*}$

同理可得

$\begin{equation*} \left|-\varepsilon\sum_{j=\frac{3N}{4}-1}^{N}[\eta(x_{j})] \{\xi'(x_{j})\}\right| \leq CN^{-(k+\frac{1}{2})} \left\|\xi \right\|_{\varepsilon}. \end{equation*}$

综上可得

$\begin{equation} |\Gamma_3| \leq CN^{-(k+\frac{1}{2})} \left\|\xi \right\|_{\varepsilon}. \end{equation}$

对于 $\Gamma_4$ 的分析可以类似于 $\Gamma_3$. 利用 (4.7) 式, 可得

$\begin{aligned} |\Gamma_4| &\leq \left|\sum_{j=0}^{\frac{N}{4}+1} \lambda_j [\eta(x_{j})] [\xi(x_{j})]\right| +\left|\sum_{j=\frac{3N}{4}-1}^{N} \lambda_j [\eta(x_{j})] [\xi(x_{j})]\right| \\ &\leq C \left(\sum_{j=0}^{\frac{N}{4}+1} \lambda_j [\eta(x_{j})]^2\right)^{\frac{1}{2}} \left(\sum_{j=0}^{\frac{N}{4}+1} \lambda_j [\xi(x_{j})]^2\right)^{\frac{1}{2}} \\ & +C \left(\sum_{j=\frac{3N}{4}-1}^{N} \lambda_j [\eta(x_{j})]^2\right)^{\frac{1}{2}} \left(\sum_{j=\frac{3N}{4}-1}^{N} \lambda_j [\xi(x_{j})]^2\right)^{\frac{1}{2}} \\ &\leq C \left( \lambda_0 \left\| \eta\right\|_{L^{\infty}(I_{1})}^2 +\sum_{j=1}^{\frac{N}{4}+1}\lambda_j \left\| \eta\right\|_{L^{\infty}(I_{j}\cup I_{j+1})}^2 \right )^{\frac{1}{2}} \left\|\xi \right\|_{\varepsilon} \\ & + C \left( \lambda_N \left\| \eta\right\|_{L^{\infty}(I_{N})}^2 +\sum_{j=\frac{3N}{4}-1}^{N-1}\lambda_j \left\| \eta\right\|_{L^{\infty}(I_{j}\cup I_{j+1})}^2 \right )^{\frac{1}{2}} \left\|\xi \right\|_{\varepsilon} \\ &\leq CN^{-k} \left\|\xi \right\|_{\varepsilon}. \end{aligned}$

现在我们来考虑 $\Gamma_5$ 和 $\Gamma_6$, 将其分成 $1\leq j \leq \frac{N}{4}+1$, $\frac{N}{4}+2 \leq j \leq \frac{3N}{4}-1$ 和 $\frac{3N}{4}\leq j \leq N$ 三部分进行分析. 对于 $1\leq j \leq \frac{N}{4}+1$, 利用 (4.2) 和 (4.3) 式可以得到

$\begin{equation*} \begin{aligned} & -\sum_{j=1}^{\frac{N}{4}+1} \int_{I_{j}} b(x)\eta\xi'{\rm d}x -\sum_{j=1}^{N} b(x_{j}) [\xi(x_{j})] \eta(x_{j}^{-})\\ &=-\sum_{j=1}^{\frac{N}{4}+1} \int_{I_{j}} \left( b(x)-b(x_{j-\frac{1}{2}}) \right)\eta\xi'{\rm d}x -\sum_{j=1}^{\frac{N}{4}+1} \int_{I_{j}} b(x_{j-\frac{1}{2}})\eta\xi'{\rm d}x -\sum_{j=1}^{\frac{N}{4}+1} b(x_{j}) [\xi(x_{j})] \eta(x_{j}^{-})\\ &=-\sum_{j=1}^{\frac{N}{4}+1} \int_{I_{j}} \left( b(x)-b(x_{j-\frac{1}{2}}) \right)\eta\xi'{\rm d}x, \end{aligned} \end{equation*}$

其中 $b(x_{j-\frac{1}{2}})$ 是 $b(x)$ 在区间 $[x_{j-1},x_j]$ 的中点 $x_{j-\frac{1}{2}}$ 处的取值. 由于 $b(x)$ 是一个充分光滑的函数, 那么利用 Lagrange 中值定理可知在 $x$ 和 $x_{j}$ 之间存在一点 $\chi$ 使得 $b(x)-b(x_{j-\frac{1}{2}})=b'(\chi)(x-x_{j-\frac{1}{2}})$ 成立. 因此, 使用逆不等式和 (4.7) 式, 可得

$\begin{equation*} \begin{aligned} \left|-\sum_{j=1}^{\frac{N}{4}+1} \int_{I_{j}} \left( b(x)-b(x_{j-\frac{1}{2}}) \right)\eta\xi'{\rm d}x\right| &=\left|-\sum_{j=1}^{\frac{N}{4}+1} \int_{I_{j}} b'(\chi)(x-x_{j-\frac{1}{2}}) \eta\xi'{\rm d}x\right|\\ &\leq C\sum_{j=1}^{\frac{N}{4}+1} h_j \left\| \eta\right\|_{L^{\infty}(I_j)} \left\| \xi'\right\|_{L^{1}(I_j)}\\ &\leq C\sum_{j=1}^{\frac{N}{4}+1} h_j \left\| \eta\right\|_{L^{\infty}(I_j)} h_{j}^{-\frac{1}{2}} \left\| \xi\right\|_{I_j}\\ &\leq CN^{-(k+1)}\left\|\xi \right\|_{\varepsilon}. \end{aligned} \end{equation*}$

对于 $\frac{3N}{4}\leq j \leq N$, 同理可得

$\begin{equation*} \left|-\sum_{j=\frac{3N}{4}}^{N} \int_{I_{j}} \left( b(x)-b(x_{j-\frac{1}{2}}) \right)\eta\xi'{\rm d}x\right|\leq CN^{-(k+1)}\left\|\xi \right\|_{\varepsilon}. \end{equation*}$

对于 $\frac{N}{4}+2 \leq j \leq \frac{3N}{4}-1$, 我们利用逆不等式, (3.8), (3.9), (4.4), (4.6), (4.7) 式, 通过简单推导可得

$\begin{equation*} \left|-\sum_{j=\frac{N}{4}+2}^{\frac{3N}{4}-1} \int_{I_{j}} b(x)\eta\xi'{\rm d}x -\sum_{j=1}^{N} b(x_{j}) [\xi(x_{j})] \eta(x_{j}^{-})\right|\leq CN^{-(k+\frac{1}{2})}\left\|\xi \right\|_{\varepsilon}. \end{equation*}$

综上所述, 我们可以得到以下估计

$\begin{equation} \left| \Gamma_5 +\Gamma_6 \right| \leq CN^{-(k+\frac{1}{2})}\left\|\xi \right\|_{\varepsilon}. \end{equation}$

对于 $\Gamma_7$, 利用 Hölder 不等式和 (4.13) 式可得

$\left|\Gamma_{7}\right| \leq C\|\eta\|_{\varepsilon}\|\xi\|_{\varepsilon} \leq C N^{-k}\|\xi\|_{\varepsilon}.$

最后, 将 (5.2)-(5.7) 式代入到 (4.13) 式, 有

$\|\xi\|_{\varepsilon} \leq C N^{-k}.$

现在我们给出本文的主要结论.

定理 5.1 设 $u$ 和 $u_N$ 分别是问题 (1.1) 和问题 (3.10) 的解, 并令 $\lambda_j=N(j=0,1,\cdots,N)$. 则在 Bakhvalov-type 网格上有

$\begin{equation*} \left\| u- u_{N} \right\|_{\varepsilon} \leq CN^{-k}. \end{equation*}$

证 由三角不等式, (3.10) 和 (5.8) 式可得

$\begin{equation*} \left\| u- u_{N} \right\|_{\varepsilon} \leq \left\| u- \Pi u \right\|_{\varepsilon} +\left\| \Pi u- u_{N} \right\|_{\varepsilon} \leq CN^{-k}. \end{equation*}$

证毕.

6 数值实验与结果分析

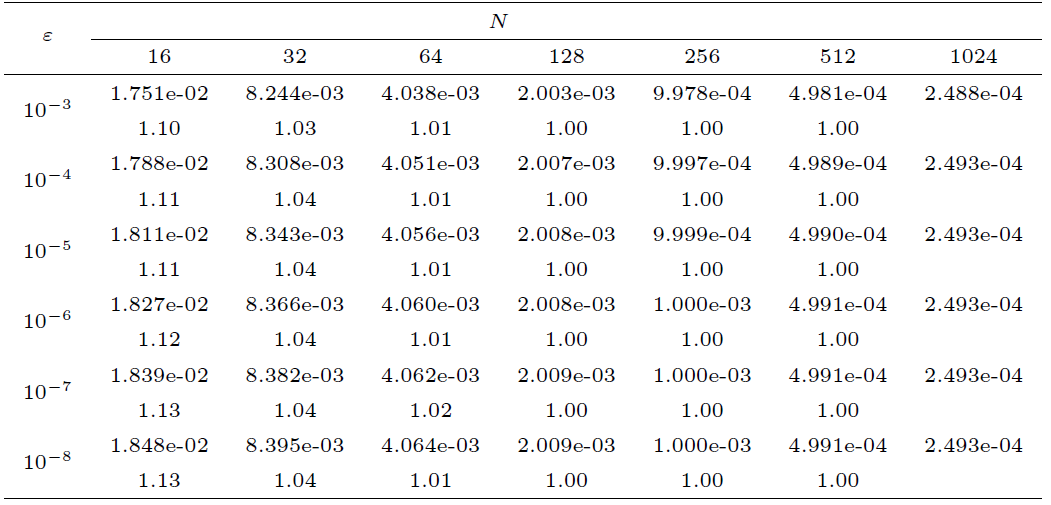
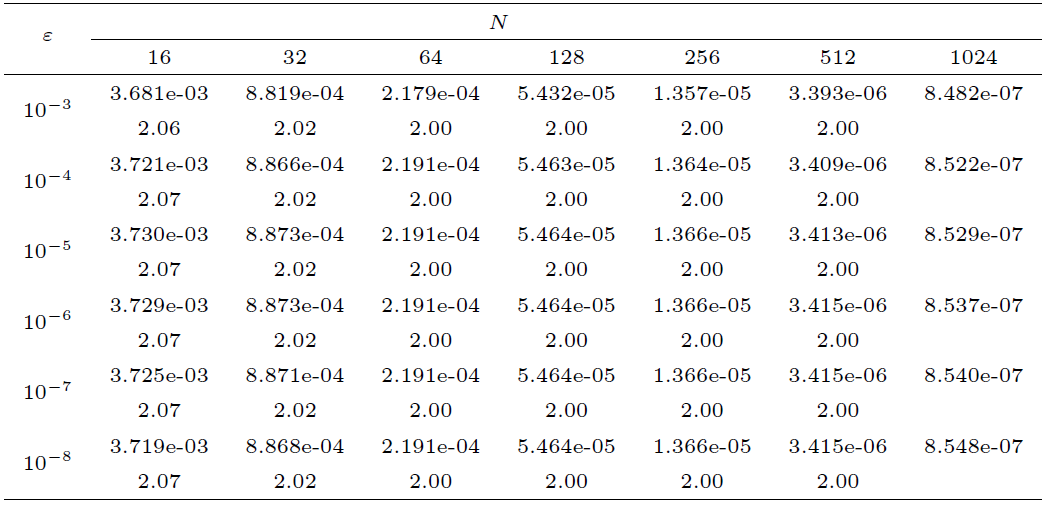
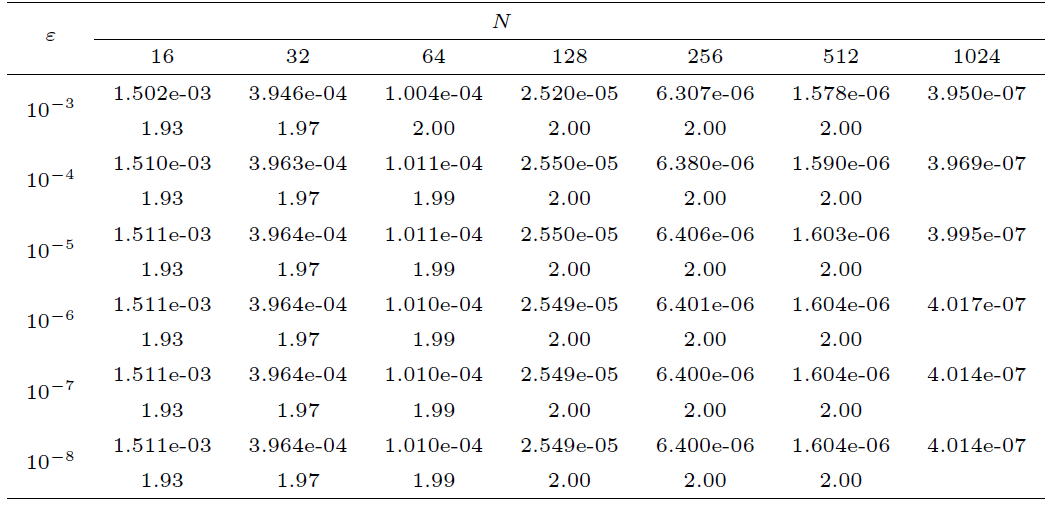
为了验证本文所提出的 NIPG 有限元方法的有效性, 我们用两个具体例子来进行数值实验. 考虑到精确解难以求出, 我们使用如下双网格原理来计算数值解的能量范数

$\begin{equation} E^{N}=\left\|u_{N}-u_{2N} \right\|_{\varepsilon}. \end{equation}$

基于该误差估计 (6.1) 式, 定义收敛阶的计算公式如下

$\rho^{N}=\log _{2}\left(\frac{E^{N}}{E^{2 N}}\right).$

在以下所有的计算中, 取 $\sigma=k+1$.

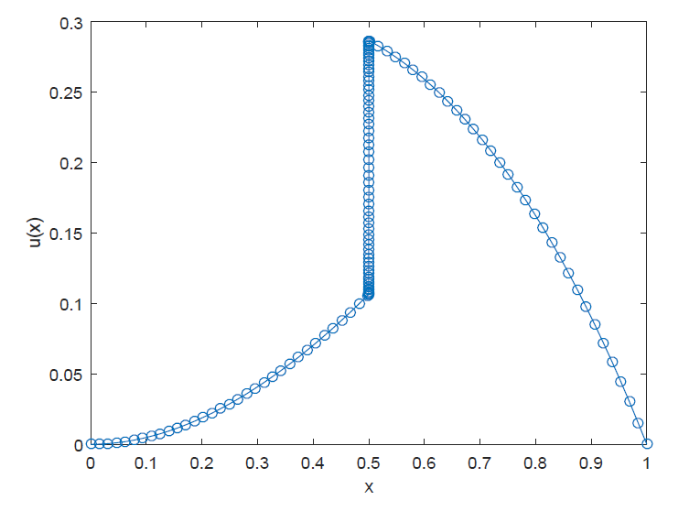
例 1考虑如下常系数对流扩散方程

$\left\{\begin{array}{l}-\varepsilon u^{\prime \prime}(x)+b(x) u^{\prime}(x)+u(x)=x, x \in \Omega, \\u(0)=u(1)=0\end{array}\right.$

其中

$\begin{eqnarray*} b(x)= \begin{cases} 1, &x \leq 0.5,\\ -1, &x>0.5. \end{cases} \end{eqnarray*}$

当 $\varepsilon=10^{-j}(j=3,\cdots,8)$ 和 $N=16,32,\cdots,1024$ 时, 表1 和表2 分别给出了在 $k=1$ 和 $k=2$ 时, NIPG 方法计算得到的能量误差和相应的收敛阶, 其中每一个 $\varepsilon$ 对应的第一行表示能量误差 $E^{N}$, 第二行表示相应的收敛阶 $\rho^{N}$. 图1 给出了$N=128,\varepsilon=10^{-4}$ 时, 数值解的变化曲线图. 进一步验证了数值解在不连续点 $x=0.5$ 附近存在内点层.

表1   当 $k=1$ 时, 例 1 的数值结果

新窗口打开| 下载CSV


表2   当 $k=2$ 时, 例 1 的数值结果

新窗口打开| 下载CSV


图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   例 1 的数值解曲线图


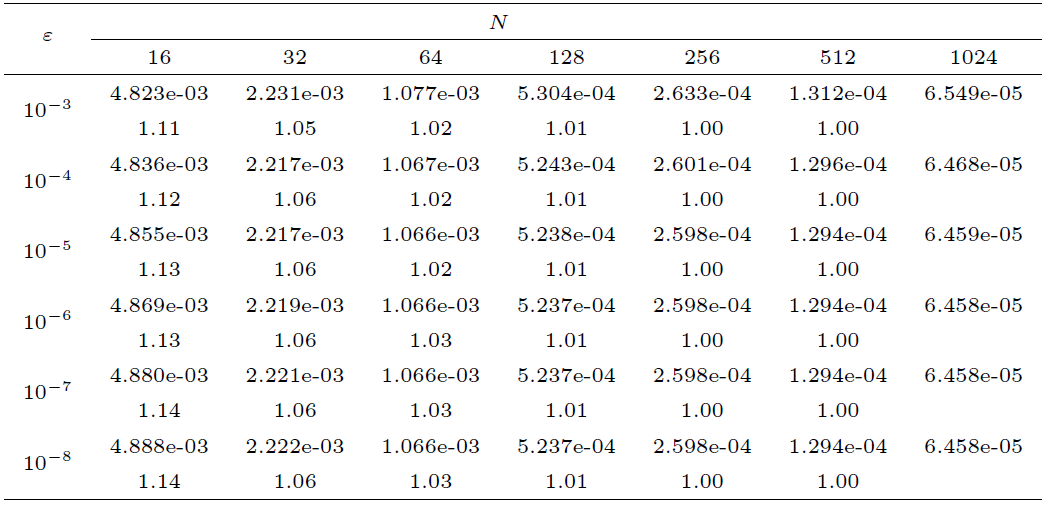
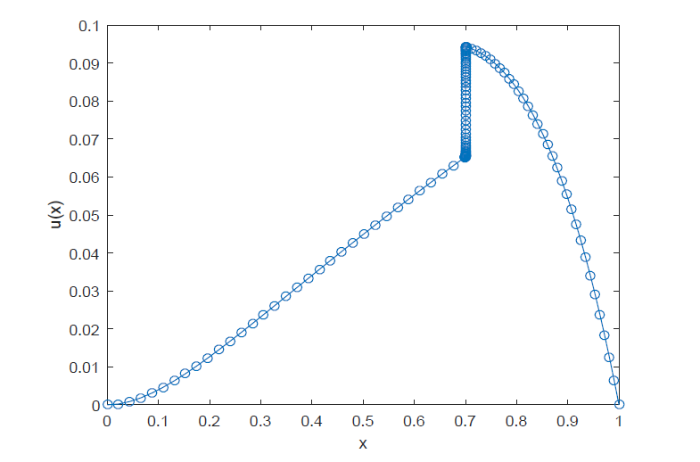
例 2 考虑如下变系数对流扩散方程

$\left\{\begin{array}{l}-\varepsilon u^{\prime \prime}(x)+b(x) u^{\prime}(x)+7 u(x)=x, x \in \Omega, \\u(0)=u(1)=0,\end{array}\right.$

其中

$\begin{eqnarray*} b(x)= \begin{cases} 3x^2+1, &x \leq 0.7,\\[1mm] -\frac{10}{7}x, &x>0.7. \end{cases} \end{eqnarray*}$

对于不同的 $\varepsilon$ 和 $N$, 表3 和表4 分别列出了 $k=1,2$ 时, NIPG 方法计算问题 (6.4) 得到的能量误差和收敛阶. 当 $N=128,\varepsilon=10^{-4}$ 时, 图2 画出了数值解的曲线图. 该图验证了数值解在不连续点 $x=0.7$ 附近存在内点层.

表3   当 $k=1$ 时, 例 2 的数值结果

新窗口打开| 下载CSV


表4   当 $k=2$ 时, 例 2 的数值结果

新窗口打开| 下载CSV


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   例 2 的数值解曲线图


综合上述两例, 由表1-4 中的数值结果可以看出, 本文提出的 NIPG 方法在 Bakhvalov-type 网格下能达到 $k$ 阶最优一致收敛.

参考文献

Zhang J, Ma X Q, Lv Y H. Finite element method on Shishkin mesh for a singularly perturbed problem with an interior layer. Applied Mathematics Letters, 2021, 121: 107509

[本文引用: 5]

Roos H G, Stynes M, Tobiska L. Numerical Methods for Singularly Perturbed Differential Equation. Berlin: Springer, 2008

[本文引用: 1]

Prabha T, Chandru M, Shanthi V.

Hybrid difference scheme for singularly perturbed reaction-convection-diffusion problem with boundary and interior layers

Applied Mathematics and Computation, 2017, 314: 237-256

[本文引用: 1]

Chandru M, Prabha T, Shanthi V.

A parameter robust higher order numerical method for singularly perturbed two parameter problems with non-smooth data

Journal of Computational and Applied Mathematics, 2017, 309: 11-27

[本文引用: 1]

Zarin H, Gordic S.

Numerical solving of singularly perturbed boundary value problems with discontinuities

Novi Sad Journal of Mathematics, 2012, 42(1): 131-145

[本文引用: 1]

Babu A R, Ramanujam N.

The SDFEM for singularly perturbed convection-diffusion problems with discontinuous source term arising in the chemical reactor theory

International Journal of Computer Mathematics, 2011, 88(8): 1664-1680

[本文引用: 1]

Linß T, Stynes M.

Numerical methods on Shishkin meshes for linear convection-diffusion problems

Computer Methods in Applied Mechanics and Engineering, 2001, 190(28): 3527-3542

[本文引用: 1]

Zarin H, Roos H G.

Interior penalty discontinuous approximations of convection-diffusion problems with parabolic layers

Numerische Mathematik, 2005, 100(4): 735-759

[本文引用: 1]

Zarin H.

On discontinuous Galerkin finite element method for singularly perturbed delay differential equations

Applied Mathematics Letters, 2014, 38: 27-32

[本文引用: 1]

Roos H G, Zarin H.

A supercloseness result for the discontinuous Galerkin stabilization of convection-diffusion problems on Shishkin meshes

Numerical Methods for Partial Differential Equations, 2007, 23(6): 1560-1576

[本文引用: 1]

Zhu P, Yang Y B, Yin Y H.

Higher order uniformly convergent NIPG methods for 1-d singularly perturbed problems of convection-diffusion type

Applied Mathematical Modelling, 2015, 39(22): 6806-6816

[本文引用: 2]

Zhang J, Liu X W.

Optimal order of uniform convergence for finite element method on Bakhvalov-type meshes

Journal of Scientific Computing, 2020, 85(1): Article 2

[本文引用: 1]

Cheng Y.

On the local discontinuous Galerkin method for singularly perturbed problem with two parameters

Journal of Computational and Applied Mathematics, 2021, 392(22): 113485

[本文引用: 2]

Ciarlet P G.

The Finite Element Method for Elliptic Problems

Philadelphia: SIAM, 2002

[本文引用: 1]

Ma X Q, Zhang J.

Supercloseness analysis of the nonsymmetric interior penalty Galerkin method for a singularly perturbed problem on Bakhvalov-type mesh

Applied Mathematics Letters, 2023, 144: 108701

[本文引用: 1]

Zhu P, Xie Z Q, Zhou S Z.

A coupled continuous-discontinuous FEM approach for convection diffusion equations

Acta Math Sci, 2011, 31B(2): 601-612

[本文引用: 2]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发