带间断系数的奇异摄动对流扩散方程的 NIPG 有限元方法

数学物理学报 ›› 2024, Vol. 44 ›› Issue (6): 1499-1510.

带间断系数的奇异摄动对流扩散方程的 NIPG 有限元方法

徐磊(),刘利斌^*()

南宁师范大学广西应用数学中心南宁 530100

收稿日期:2023-01-15 修回日期:2024-04-17 出版日期:2024-12-26 发布日期:2024-11-22
通讯作者: ^*刘利斌, Email：liulibin969@163.com
作者简介:徐磊, Email：xulei19980919@163.com
基金资助:
国家自然科学基金(12361087);广西科技基地和人才专项(AD23023003);广西研究生教育创新计划资助(YCSW2023438)

Uniformly Convergent NIPG Methods for a Singularly Perturbed Convection-Diffusion Problem with a Discontinuous Convection Coefficient

Xu Lei(),Liu Libin^*()

Center for Applied Mathematics of Guangxi, Nanning Normal University, Nanning 530100

Received:2023-01-15 Revised:2024-04-17 Online:2024-12-26 Published:2024-11-22
Supported by:
National Science Foundation of China(12361087);Guangxi Science and Techology Program(AD23023003);Innovation Project of Guangxi Graduate Education(YCSW2023438)

摘要/Abstract

摘要：

针对带间断系数的奇异摄动对流扩散方程, 该文在 Bakhvalov-type 网格下, 构造了一种 NIPG 高阶有限元方法. 基于 Gauß Radau 投影和 Lagrange 插值, 推导出 NIPG 方法的最优一致收敛性.最后的数值实验支持了作者的理论结果.

关键词: 奇异摄动, 间断系数, NIPG 方法, Bakhvalov-type 网格

Abstract:

In this paper, a higher order NIPG method on a Bakhvalov-type mesh for a singularly perturbed convection-diffusion problem with a discontinuous convection coefficient is studied. Based on Gauß Radau interpolation and Lagrange interpolation, the convergence of optimal order in an energy norm is derived. Numerical experiments are proposed to confirm our theoretical results.

Key words: Singularly perturbed, Nonsmooth coefficient, NIPG method, Bakhvalov-type mesh

中图分类号:

0175.23

徐磊, 刘利斌. 带间断系数的奇异摄动对流扩散方程的 NIPG 有限元方法[J]. 数学物理学报, 2024, 44(6): 1499-1510.

Xu Lei, Liu Libin. Uniformly Convergent NIPG Methods for a Singularly Perturbed Convection-Diffusion Problem with a Discontinuous Convection Coefficient[J]. Acta mathematica scientia,Series A, 2024, 44(6): 1499-1510.

图/表 6

表1

表2

图1

表3

表4

图2

参考文献 16

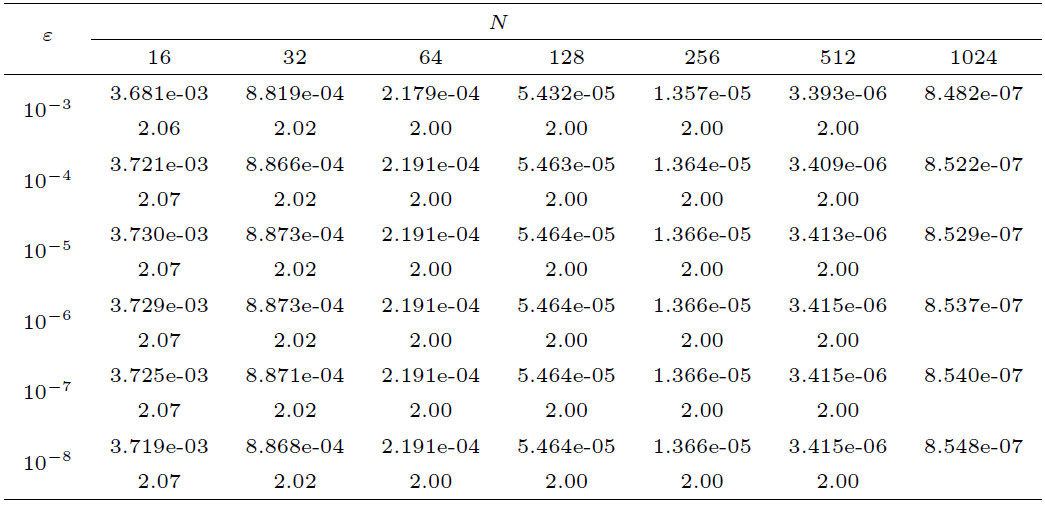
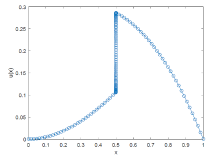
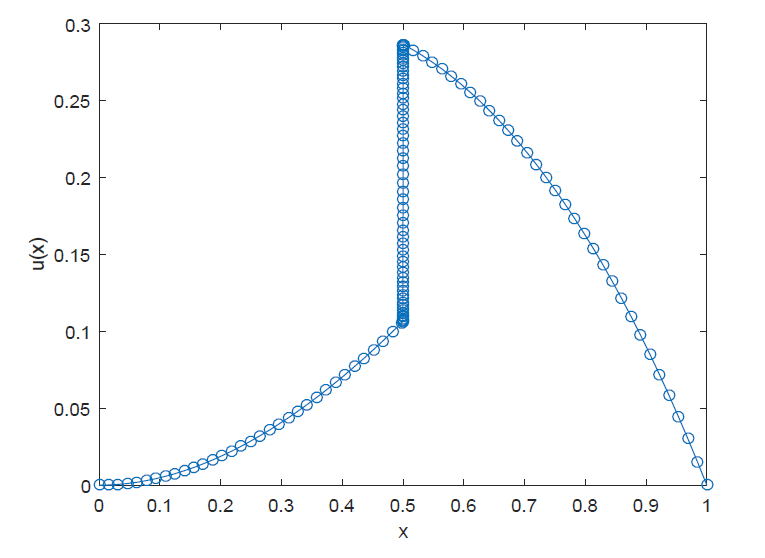
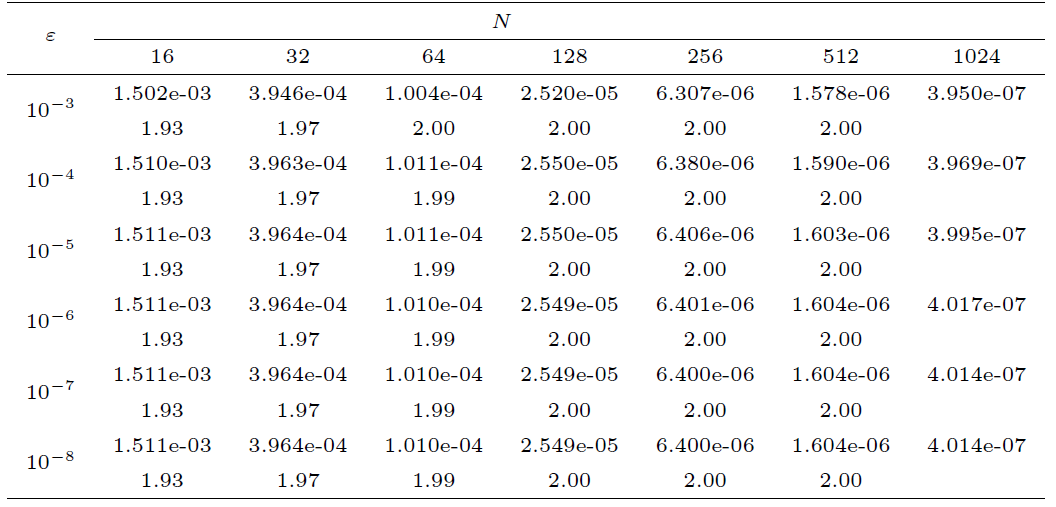
[1]	Zhang J, Ma X Q, Lv Y H. Finite element method on Shishkin mesh for a singularly perturbed problem with an interior layer. Applied Mathematics Letters, 2021, 121: 107509
[2]	Roos H G, Stynes M, Tobiska L. Numerical Methods for Singularly Perturbed Differential Equation. Berlin: Springer, 2008
[3]	Prabha T, Chandru M, Shanthi V. Hybrid difference scheme for singularly perturbed reaction-convection-diffusion problem with boundary and interior layers. Applied Mathematics and Computation, 2017, 314: 237-256
[4]	Chandru M, Prabha T, Shanthi V. A parameter robust higher order numerical method for singularly perturbed two parameter problems with non-smooth data. Journal of Computational and Applied Mathematics, 2017, 309: 11-27
[5]	Zarin H, Gordic S. Numerical solving of singularly perturbed boundary value problems with discontinuities. Novi Sad Journal of Mathematics, 2012, 42(1): 131-145
[6]	Babu A R, Ramanujam N. The SDFEM for singularly perturbed convection-diffusion problems with discontinuous source term arising in the chemical reactor theory. International Journal of Computer Mathematics, 2011, 88(8): 1664-1680
[7]	Linß T, Stynes M. Numerical methods on Shishkin meshes for linear convection-diffusion problems. Computer Methods in Applied Mechanics and Engineering, 2001, 190(28): 3527-3542
[8]	Zarin H, Roos H G. Interior penalty discontinuous approximations of convection-diffusion problems with parabolic layers. Numerische Mathematik, 2005, 100(4): 735-759
[9]	Zarin H. On discontinuous Galerkin finite element method for singularly perturbed delay differential equations. Applied Mathematics Letters, 2014, 38: 27-32
[10]	Roos H G, Zarin H. A supercloseness result for the discontinuous Galerkin stabilization of convection-diffusion problems on Shishkin meshes. Numerical Methods for Partial Differential Equations, 2007, 23(6): 1560-1576
[11]	Zhu P, Yang Y B, Yin Y H. Higher order uniformly convergent NIPG methods for 1-d singularly perturbed problems of convection-diffusion type. Applied Mathematical Modelling, 2015, 39(22): 6806-6816
[12]	Zhang J, Liu X W. Optimal order of uniform convergence for finite element method on Bakhvalov-type meshes. Journal of Scientific Computing, 2020, 85(1): Article 2
[13]	Cheng Y. On the local discontinuous Galerkin method for singularly perturbed problem with two parameters. Journal of Computational and Applied Mathematics, 2021, 392(22): 113485
[14]	Ciarlet P G. The Finite Element Method for Elliptic Problems. Philadelphia: SIAM, 2002
[15]	Ma X Q, Zhang J. Supercloseness analysis of the nonsymmetric interior penalty Galerkin method for a singularly perturbed problem on Bakhvalov-type mesh. Applied Mathematics Letters, 2023, 144: 108701
[16]	Zhu P, Xie Z Q, Zhou S Z. A coupled continuous-discontinuous FEM approach for convection diffusion equations. Acta Math Sci, 2011, 31B(2): 601-612