1 引言
近年来, 保险公司的最优风险控制与投资问题已经受到了广泛的关注. 保险公司可以将资金投资于金融市场来增加收益. 采用合适的风险控制策略可以帮助保险公司规避保险风险. 一种比较常见且有效的规避保险风险的方法是购买再保险.
有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题.
动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题.
以上所有的研究都假设市场是无摩擦的, 忽略了在金融市场中投资的交易成本. 然而, 在实际的投资交易中, 交易成本是不可避免的, 投资于风险资产时通常需要支付相应的交易费用, 这会一定程度上降低交易策略的收益. 因此, 不应忽视交易成本对投资绩效的影响. Yoshimoto[22 ] 研究了受交易成本影响的投资组合优化问题, 实证分析表明, 忽略交易成本会导致投资组合效率低下. He 和 Liang[23 ] 考虑金融市场中具有固定和比例交易成本, 研究了保险公司的最优融资和股利控制问题. Hobson 等[24 ] 求解了金融市场中具有比例交易成本和单一风险资产的默顿问题. Mei 和 Nogales[25 ] 假设金融市场中存在多个风险资产和比例交易成本, 在收益可预测的情况下研究了多阶段的投资组合选择问题. Melnyk 等[26 ] 探讨了在等弹性递归效用下, 具有小交易成本的终身消费和投资组合选择问题. Gârleanu 和 Pedersen[27 ] 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近.
参考文献 [29 ], 考虑二次型交易成本, 该文研究动态均值-方差准则下保险公司的最优风险控制与投资问题. 假设金融市场由无风险资产和多种风险资产组成, 并且运用跳扩散过程来描述保险公司单位风险的动态模型. 与现有的均值-方差准则下的最优风险控制和投资问题的文献相比, 包括文献 [18 ⇓ ⇓ -21 ] 等, 本文将二次型交易成本纳入模型, 并且假设保险风险与金融风险存在相关性. 虽然 Garleanu 和 Pedersen[28 ] , Ma 等[29 ] 和 Bensoussan 等[30 ] 均考虑了二次型交易成本, 但是这些工作并没有考虑到保险风险控制以及保险风险与金融风险的相关性. 在博弈论框架下, 通过求解扩展的 HJB 方程组, 我们得到了依赖于矩阵 Riccati 方程组的解的均衡策略和相应的值函数. 此外, 还进一步研究了一些特殊情况, 并给出了均衡策略和值函数的更具体的表达式. 通过数值分析发现, 随着交易成本水平或相关系数的增加, 投资的增长率会减小. 并且交易成本水平的增加会导致更差的有效前沿.
该文第 2 节介绍了单位风险过程, 风险资产价格过程, 以及优化目标. 第节求解优化问题, 推导出均衡风险控制和投资策略以及相应的值函数. 同时还考虑了一些特殊情形. 第四节通过数值算例分析了重要参数对均衡策略和有效前沿的影响. 第五节是对该文的总结.
2 模型建立
令 $\left( {\Omega, \mathcal{F},{{\left\{ {{\mathcal{F}_t}} \right\}}_{t \in \left[ {0,T} \right]}},\mathbb{P}} \right)$ ${\left\{ {{\mathcal{F}_t}} \right\}_{t \in \left[ {0,T} \right]}}$ $T > 0$ ${\left\{ {{\mathcal{F}_t}} \right\}_{t \in \left[ {0,T} \right]}}$
(2.1) $\begin{equation} {\rm d}R(t) = \alpha {\rm d}t + {\sigma _0}{\rm d}{W_0}(t) + \int_0^\infty {yN\left( {{\rm d}t,{\rm d}y} \right)}, \end{equation}$
其中 $\alpha, \sigma _0 \geqslant 0$ $N\left( {{\rm d}t,{\rm d}y} \right)$ ${W_0}(t)$ $N\left( {{\rm d}t,{\rm d}y} \right)$ $\tilde N\left( {{\rm d}t,{\rm d}y} \right) = N\left( {{\rm d}t,{\rm d}y} \right) - v\left( {{\rm d}y} \right){\rm d}t$ $N\left( {{\rm d}t,{\rm d}y} \right)$
保险公司可以通过控制保单数来管理保险风险, 设 $p(t)$ $t$ $p(t)$ $p(t)\left( {c{\rm d}t - {\rm d}R(t)} \right)$ $c > \alpha + \int_0^\infty {yv\left( {{\rm d}y} \right)} $
为了增加收益, 保险公司可投资到由一个无风险资产与 $n$ ${S_0}(t)$
(2.2) $\begin{equation} {\rm d}{S_0}(t) = {r_0}{S_0}(t){\rm d}t, \end{equation}$
其中 ${r_0} > 0$ $\boldsymbol{S}(t) = {\left[ {{S_1}(t),{S_2}(t), \cdots, {S_n}(t)} \right]^ \top }$
(2.3) $\begin{equation} {\rm d}\boldsymbol{S}(t) = \left[ {{r_0}\boldsymbol{S}(t) + \boldsymbol{\mu} (t)} \right]{\rm d}t + {\boldsymbol{\sigma} _s}\left( {\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}{\rm d}{W_0}(t) + \boldsymbol{\hat \rho}{\rm d}{\boldsymbol{W}_1}(t)} \right). \end{equation}$
这里 ${\boldsymbol{\sigma} _s} = {\left( {{\sigma _{ij}}} \right)_{n \times n}}$ $n$ $\boldsymbol{\mu} (t) = {\left[ {{\mu _1}(t),{\mu _2}(t), \cdots, {\mu _n}(t)} \right]^ \top }$ ${\boldsymbol{W}_1}(t) = {\left[ {{W_{11}}(t),{W_{12}}(t), \cdots, {W_{1n}}(t)} \right]^ \top }$ ${W_0}(t)$ $N\left( {{\rm d}t,{\rm d}y} \right)$ $n$ $\boldsymbol{\rho} = {\rm diag}\left( {{\rho _1},{\rho _2}, \cdots {\rho _n}} \right)$ $\boldsymbol{\hat \rho} = {\rm diag}\left( {\sqrt {1 - \rho _1^2}, \sqrt {1 - \rho _2^2}, \cdots, \sqrt {1 - \rho _n^2} } \right)$ ${\boldsymbol{I}_{n \times 1}}$
在现实中, 投资策略的选取会受到市场摩擦的影响, 如交易成本, 市场波动, 资本利得税等. 其中交易成本最为常见, 并受到研究人员和投资者的广泛关注. 交易成本会在一定程度上影响投资者的投资组合选择, 且忽视交易成本可能会导致较大损失和投资效率的降低. 设 ${\pi _i}(t)$ $i$ $i = 1,2,\cdots,n$ . 记 $\boldsymbol{\pi} (t) = {\left[ {{\pi _1}(t),{\pi _2}(t), \cdots, {\pi _n}(t)} \right]^ \top }$ . Gârleanu 和 Pedersen[28 ] 指出资产头寸的非光滑变动可能会导致无限的交易成本, 所以本文只考虑光滑或者绝对连续的投资组合 $\boldsymbol{\pi} (t)$ . 即存在 $\boldsymbol{\varphi} (t) = {\left[ {{\varphi _1}(t),{\varphi _2}(t), \cdots, {\varphi _n}(t)} \right]^ \top }$
(2.4) $\begin{equation} {\rm d}\boldsymbol{\pi} (t) = \boldsymbol{\varphi} (t){\rm d}t, \end{equation}$
以下将 $\boldsymbol{\varphi} (t)$ [28 ] , 假设交易 $\boldsymbol{\varphi} (t){\rm d}t$ $\boldsymbol{\varphi} (t){\rm d}t$
(2.5) $\begin{equation} {\boldsymbol{S}^E}(t): = \boldsymbol{S}(t) + \frac{1}{2}\boldsymbol{\Lambda} \boldsymbol{\varphi} (t), \end{equation}$
其中 $\boldsymbol{\Lambda} $ $n$ ${\boldsymbol{S}^E}(t)$ $\boldsymbol{\varphi} (t)$
(2.6) $\begin{equation}\label{totalcost} \operatorname{Cos} t\left( {\boldsymbol{\varphi} (t)} \right): = \boldsymbol{\varphi} {(t)^ \top }{\boldsymbol{S}^E}(t) = \boldsymbol{\varphi} {(t)^ \top }\boldsymbol{S}(t) + \frac{1}{2}\boldsymbol{\varphi} {(t)^ \top }\boldsymbol{\Lambda} \boldsymbol{\varphi} (t). \end{equation}$
(2.6) 式右边第一项为交易 $\boldsymbol{\varphi} (t)$ $\boldsymbol{S}(t)$
令 $u(t){: = }{\left( {p(t),\boldsymbol{\varphi} (t)} \right)^ \top }$ ${X^u}(t)$ ${X^u}(t)$
(2.7) $\begin{equation}\label{wealth} \begin{split} {\rm d}{X^u}(t) &= p(t)\left( {c{\rm d}t - {\rm d}R(t)} \right) + {r_0}{\pi _0}(t){S_0}(t){\rm d}t + \boldsymbol{\pi} {(t)^ \top }{\rm d}\boldsymbol{S}(t) - \frac{1}{2}\boldsymbol{\varphi} {(t)^ \top }\boldsymbol{\Lambda} \boldsymbol{\varphi} (t){\rm d}t \hfill \\ &= \left[ {{r_0}{X^u}(t) + p(t)\left( {c - \alpha } \right) + \boldsymbol{\pi} {{(t)}^ \top }\boldsymbol{\mu} (t) - \frac{1}{2}\boldsymbol{\varphi} {{(t)}^ \top }\boldsymbol{\Lambda} \boldsymbol{\varphi} (t)} \right]{\rm d}t \hfill \\ &\quad + \left( {\boldsymbol{\pi} {{(t)}^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}} - p(t){\sigma _0}} \right){\rm d}{W_0}(t) + \boldsymbol{\pi} {(t)^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\hat \rho} {\rm d}{\boldsymbol{W}_1}(t) - p(t)\int_0^\infty {yN\left( {{\rm d}t,{\rm d}y} \right)}. \hfill \\ \end{split} \end{equation}$
定义 2.1 如果风险控制与投资策略 $u(t){= }{\left( {p(t),\boldsymbol{\varphi} (t)} \right)^ \top }$
(1) $u(t)$ ${\left\{ {{\mathcal{F}_t}} \right\}_{t \in \left[ {0,T} \right]}}$
(2) 对任意 $t \in \left[ {0,T} \right]$ $p(t) \in \left[ {0, + \infty } \right)$
(3) $\mathbb{E}\left[ {\int_0^T {\left( {p{{(t)}^2} + {{\left| {\boldsymbol{\varphi} (t)} \right|}^2}} \right){\rm d}t} } \right] < + \infty $
令 $\Pi $
(2.8) $\begin{equation} {J^u}\left( {t,x,\boldsymbol{\pi} } \right) = {\mathbb{E}_{t,x,\boldsymbol{\pi} }}\left[ {{X^u}\left( T \right)} \right] - \frac{\gamma }{2}Va{r_{t,x,\boldsymbol{\pi} }}\left[ {{X^u}\left( T \right)} \right], \end{equation}$
其中 ${\mathbb{E}_{t,x,\boldsymbol{\pi} }}\left[ \bullet \right] = {\mathbb{E}}\left[ {\left. \bullet \right|{X^u}(t) = x,\boldsymbol{\pi} (t) = \boldsymbol{\pi} } \right]$ $Va{r_{t,x,\boldsymbol{\pi} }}\left[ \bullet \right] = Var\left[ {\left. \bullet \right|{X^u}(t) = x,\boldsymbol{\pi} (t) = \boldsymbol{\pi} } \right]$ $\gamma$
(2.9) $\begin{equation}\label{Optobj} \mathop {\sup }\limits_{u \in \Pi } {J^u}\left( {{t},x,\boldsymbol{\pi} } \right). \end{equation}$
由于 ${J^u}\left( {{t},x,\boldsymbol{\pi} } \right)$ ${\mathbb{E}_{t,x,\boldsymbol{\pi} }}\left[ {{X^u}\left( T \right)} \right]$ [17 ] 和 Björk 等[19 ] , 我们给出时间一致的均衡风险控制与投资策略的定义.
定义 2.2 设 ${u^ * }(t) = \left( {{p^ * }(t),{\boldsymbol{\varphi} ^ * }(t)} \right)^ \top \in \Pi $
其中 $\varepsilon > 0$ $\left( {\tilde p,\boldsymbol{\tilde \varphi} } \right) \in \left[ {0,{ + }\infty } \right) \times {\mathbb{R}^n}$ . 如果对任意的初始状态 $\left( {t,x,\boldsymbol{\pi} } \right) \in \left[ {0,T} \right] \times {\mathbb{R}} \times {\mathbb{R}^n}$
那么 ${u^ * }(t) = \left( {{p^ * }(t),{\boldsymbol{\varphi} ^ * }(t)} \right)^ \top$
3 主要结果
本节给出问题 (2.9) 的验证定理, 并求解得到时间一致的均衡风险控制与投资策略. 首先定义一个无穷小算子. 方便起见, 令 ${C^{1,2,2}}\left( {\left[ {0,T} \right] \times \mathbb{R} \times {\mathbb{R}^n}} \right)$ $t \in \left[ {0,T} \right]$ $x \in \mathbb{R}$ $\boldsymbol{\pi} \in {\mathbb{R}^n}$ $\phi \left( {t,x,\boldsymbol{\pi} } \right)$ $\phi \left( {t,x,\boldsymbol{\pi} } \right) \in {C^{1,2,2}}\left( {\left[ {0,T} \right] \times \mathbb{R} \times {\mathbb{R}^n}} \right)$
(3.1) $\begin{align*} {\mathcal{A}^{u}}\phi \left( {t,x,\boldsymbol{\pi} } \right):= &\left[ {{r_0}x + p\left( {c - \alpha } \right) + {\boldsymbol{\pi} ^ \top }\boldsymbol{\mu} - \frac{1}{2}{\boldsymbol{\varphi} ^ \top }\boldsymbol{\Lambda} \boldsymbol{\varphi} } \right]{\phi _x}\left( {t,x,\boldsymbol{\pi} } \right) + {\phi _t}\left( {t,x,\boldsymbol{\pi} } \right) \\ &+ {\boldsymbol{\phi _\pi} }{\left( {t,x,\boldsymbol{\pi} } \right)^ \top }\boldsymbol{\varphi} + \frac{1}{2}\left( {{{\left( {{\boldsymbol{\pi} ^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}} - p{\sigma _0}} \right)}^2} + {\boldsymbol{\pi} ^ \top }{\boldsymbol{\sigma} _s}{{\boldsymbol{\hat \rho} }^2}\boldsymbol{\sigma} _s^ \top \boldsymbol{\pi} } \right){\phi _{xx}}\left( {t,x,\boldsymbol{\pi} } \right) \\ &+ \int_0^\infty {\left( {\phi \left( {t,x - py,\boldsymbol{\pi} } \right) - \phi \left( {t,x,\boldsymbol{\pi} } \right)} \right)v\left( {{\rm d}y} \right)}. \end{align*}$
下面给出问题 (2.9) 的值函数满足的扩展的 HJB 方程组及相应的验证定理.
定理 3.1 假设存在函数 $V\left( {t,x,\boldsymbol{\pi} } \right)$ $g\left( {t,x,\boldsymbol{\pi} } \right) \in {C^{1,2,2}}\left( {\left[ {0,T} \right] \times \mathbb{R} \times {\mathbb{R}^n}} \right)$
(3.2) $\begin{equation}\label{hjbequ} \mathop {\sup }\limits_{u \in \Pi } \left\{ {{\mathcal{A}^u}V\left( {t,x,\boldsymbol{\pi} } \right) - \frac{\gamma }{2}{\mathcal{A}^u}{g^2}\left( {t,x,\boldsymbol{\pi} } \right) + \gamma g\left( {t,x,\boldsymbol{\pi} } \right){\mathcal{A}^u}g\left( {t,x,\boldsymbol{\pi} } \right)} \right\} = 0, \end{equation}$
(3.3) $\begin{equation} V\left( {T,x,\boldsymbol{\pi} } \right) = x, \end{equation}$
(3.4) $\begin{equation}\label{suanzig} {\mathcal{A}^{{u^ * }}}g\left( {t,x,\boldsymbol{\pi} } \right) = 0, \end{equation}$
(3.5) $\begin{equation} g\left( {T,x,\boldsymbol{\pi} } \right) = x, \end{equation}$
(3.6) $\begin{equation} {u^ * }: = \arg \mathop {\sup }\limits_{u \in \Pi } \left\{ {{\mathcal{A}^u}V\left( {t,x,\boldsymbol{\pi} } \right) - \frac{\gamma }{2}{\mathcal{A}^u}{g^2}\left( {t,x,\boldsymbol{\pi} } \right) + \gamma g\left( {t,x,\boldsymbol{\pi} } \right){\mathcal{A}^u}g\left( {t,x,\boldsymbol{\pi} } \right)} \right\}, \end{equation}$
那么 ${u^ * }$ $V\left( {t,x,\boldsymbol{\pi} } \right) = {J^{{u^ * }}}\left( {{t},x,\boldsymbol{\pi} } \right)$ $g\left( {t,x,\boldsymbol{\pi} } \right) = {\mathbb{E}_{t,x,\boldsymbol{\pi} }}\left[ {{X^{{u^ * }}}\left( T \right)} \right]$ .
定理 3.2 对于问题 (2.9), 其均衡风险控制策略为
(3.7) $\begin{equation} {p^ * }(t) = p(t) \vee 0, \end{equation}$
(3.8) $\begin{equation}\label{pequation} \begin{gathered} \left( {c - \alpha } \right){{\rm e}^{{r_0}\left( {T - t} \right)}} + \gamma {\sigma _0}\left( {\boldsymbol{\pi} {{(t)}^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}} - p(t){\sigma _0}} \right){{\rm e}^{2{r_0}\left( {T - t} \right)}} \hfill \\ - \int_0^\infty {\left( {y{{\rm e}^{{r_0}\left( {T - t} \right)}} + \gamma p(t){y^2}{{\rm e}^{2{r_0}\left( {T - t} \right)}}} \right)v\left( {{\rm d}y} \right)} = 0. \hfill \\ \end{gathered} \end{equation}$
均衡投资策略 ${\boldsymbol{\varphi} ^ * }(t)$
(3.9) $\begin{equation}\label{phiequation} {\boldsymbol{\varphi} ^ * }(t) = {\boldsymbol{\Lambda} ^{ - 1}}\left( {2\boldsymbol{M}(t)\boldsymbol{\pi} (t) + \boldsymbol{\bar N}(t)} \right){{\rm e}^{ - {r_0}\left( {T - t} \right)}}, \end{equation}$
这里的 ${\boldsymbol{M}(t)}$ $\boldsymbol{\bar N}(t)$ $p(t)$ $p(t) \vee 0$ ).
(3.10) $\begin{equation}\label{wealthfun} V\left( {t,x,\boldsymbol{\pi} } \right) = x{{\rm e}^{{r_0}\left( {T - t} \right)}} + {\boldsymbol{\pi} ^ \top }\boldsymbol{M}(t)\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }\boldsymbol{\bar N}(t) + \bar H(t), \end{equation}$
上式中 $\bar H(t)$ $p(t)$ $p(t) \vee 0$ ).
(3.11) $\begin{equation}\label{expfun} {\mathbb{E}_{t,x,\boldsymbol{\pi} }}\left[ {{X^{{u^ * }}}\left( T \right)} \right] = g\left( {t,x,\boldsymbol{\pi} } \right) = x{{\rm e}^{{r_0}\left( {T - t} \right)}} + {\boldsymbol{\pi} ^ \top }\boldsymbol{m}(t)\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }\boldsymbol{\bar n}(t) + \bar h(t), \end{equation}$
这里的 ${\boldsymbol{m}(t)}$ $\boldsymbol{\bar n}(t)$ $\bar h(t)$ $p(t)$ $p(t) \vee 0$ ).
注 3.1 由 (3.9) 式可以看出均衡投资策略 ${\boldsymbol{\varphi} ^ * }(t)$ $\boldsymbol{\Lambda}$ $\boldsymbol{\rho} \ne {\boldsymbol{0}_{n \times n}}$ ${\boldsymbol{\varphi} ^ * }(t)$ ${p^ * }(t)$ ${\boldsymbol{\varphi} ^ * }(t)$ $\boldsymbol{\Lambda}$ ${\boldsymbol{\varphi} ^ * }(t)$ ${p^ * }(t)$ .
注 3.2 根据 (3.10) 与 (3.11) 式可以得到均值-方差有效前沿的参数表达式为 ($\gamma$
(3.12) $\begin{equation} {\mathbb{E}_{t,x,\boldsymbol{\pi} }}\left[ {{X^{{u^ * }}}\left( T \right)} \right] = g\left( {t,x,\boldsymbol{\pi} } \right) = x{{\rm e}^{{r_0}\left( {T - t} \right)}} + {\boldsymbol{\pi} ^ \top }\boldsymbol{m}(t)\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }\boldsymbol{\bar n}(t) + \bar h(t), \end{equation}$
(3.13) $\begin{equation} \begin{split} Va{r_{t,x,\boldsymbol{\pi} }}\left[ {{X^{{u^ * }}}\left( T \right)} \right] &= \frac{2}{\gamma }\left[ {g\left( {t,x,\boldsymbol{\pi} } \right) - V\left( {t,x,\boldsymbol{\pi} } \right)} \right] \hfill \\ &= \frac{2}{\gamma }\left\{ {{\boldsymbol{\pi} ^ \top }\left[ {\boldsymbol{m}(t) - \boldsymbol{M}(t)} \right]\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }\left[ {\boldsymbol{\bar n}(t) - \boldsymbol{\bar N}(t)} \right] + \bar h(t) - \bar H(t)} \right\}. \hfill \\ \end{split} \end{equation}$
命题 3.1 对任意固定的 $t \in \left[ {0,T} \right]$ $\boldsymbol{\pi} \in {\mathbb{R}^n}$
证 对任意固定的 $t \in \left[ {0,T} \right]$ $\boldsymbol{\pi} \in {\mathbb{R}^n}$
$f\left( {p,\boldsymbol{\pi} } \right)$ $p$
对于给定的 $\boldsymbol{\pi} \in {\mathbb{R}^n}$ $\mathop {\lim }\limits_{p \downarrow - \infty } f\left( {p,\boldsymbol{\pi} } \right) = + \infty $ $\mathop {\lim }\limits_{p \uparrow + \infty } f\left( {p,\boldsymbol{\pi} } \right) = - \infty $ .
因此, 由连续函数的介质定理知方程 (3.8) 存在唯一解.
均衡策略满足的方程 (3.8), (3.9), (A10), (A11) 和 (A12) 是高度非线性的, 一般来说, 很难通过求解这些方程得到均衡策略的 (半) 解析表达式. 接下来我们将关注一些特殊情况, 得到均衡策略的相对具体的表达式, 以便于后续的数值分析.
推论 3.1 当单位风险过程中没有跳跃时, 即满足 ${\rm d}R(t) = \alpha {\rm d}t + {\sigma _0}{\rm d}{W_0}(t)$ $u_1^ * (t)$
(3.14) $\begin{equation}\label{u1xing} \left\{ \begin{gathered} p_1^ * (t) = \left[ {\frac{{\left( {c - \alpha } \right){{\rm e}^{ - {r_0}\left( {T - t} \right)}} + \gamma {\sigma _0}\boldsymbol{\pi} {{(t)}^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}}}{{\gamma \sigma _0^2}}} \right] \vee 0, \hfill \\ \boldsymbol{\varphi} _1^ * (t) = {\boldsymbol{\Lambda} ^{ - 1}}\left( {2{\boldsymbol{M}_1}(t)\boldsymbol{\pi} (t) + {{\boldsymbol{\bar N}}_1}(t)} \right){{\rm e}^{ - {r_0}\left( {T - t} \right)}}, \hfill \\ \end{gathered} \right. \end{equation}$
并且最优投资份额 $\boldsymbol{\pi} _1^ * (t)$
(3.15) $\begin{equation}\label{pi1diff2} \left\{ \begin{gathered} \boldsymbol{\pi} _1^ * {(t)^{\prime \prime }} + \left( {2{{\rm e}^{ - {r_0}\left( {T - t} \right)}}{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{M}_1}(t) - {r_0}{\boldsymbol{E}_{n \times n}} - \boldsymbol{k}(t)} \right)\boldsymbol{\pi} _1^ * {(t)^\prime } \hfill \\ + \left( { - \boldsymbol{k}{{(t)}^\prime } - 2{{\rm e}^{ - {r_0}\left( {T - t} \right)}}{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{M}_1}\left( v \right)\boldsymbol{k}(t) + {r_0}\boldsymbol{k}(t)} \right)\boldsymbol{\pi} _1^ * (t) \hfill \\ + {\boldsymbol{\Lambda} ^{ - 1}}\left( {\boldsymbol{\mu} + \gamma p_1^ * (t){\sigma _0}{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}} \right) = {\boldsymbol{0}_{n \times 1}}, \hfill \\ \boldsymbol{\pi} _1^ * {\left( T \right)^\prime } = {\boldsymbol{0}_{n \times 1}}, \hfill \\ \end{gathered} \right. \end{equation}$
这里的 ${\boldsymbol{M}_1}(t)$ ${\boldsymbol{\bar N}_1}(t)$ ${p_1}(t)$ $p_1^ * (t)$ ) , $\boldsymbol{k}(t) = 2{{\rm e}^{ - {r_0}\left( {T - t} \right)}}{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{M}_1}(t)$ . 且均衡值函数为
(3.16) $\begin{equation}\label{V1exp} {V_1}\left( {t,x,\boldsymbol{\pi} } \right) = {{\rm e}^{{r_0}\left( {T - t} \right)}}x + {\boldsymbol{\pi} ^ \top }{\boldsymbol{M}_1}(t)\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }{\boldsymbol{\bar N}_1}(t) + {\bar H_1}(t), \end{equation}$
上式中 ${\bar H_1}(t)$ ${p_1}(t)$ $p_1^ * (t)$ ).
推论 3.2 当保险市场和金融市场独立时, 即 $\boldsymbol{\rho} {=}{\boldsymbol{0}_{n \times n}}$ $u_2^ * (t)$
(3.17) $\begin{equation}\label{u2xing} \left\{ \begin{gathered} \left( {c - \alpha } \right){{\rm e}^{{r_0}\left( {T - t} \right)}} - \gamma \sigma _0^2p_2^ * (t){{\rm e}^{2{r_0}\left( {T - t} \right)}} \hfill \\ - \int_0^\infty {\left( {y{{\rm e}^{{r_0}\left( {T - t} \right)}} + \gamma p_2^ * (t){y^2}{{\rm e}^{2{r_0}\left( {T - t} \right)}}} \right)v\left( {{\rm d}y} \right)} = 0, \hfill \\ \boldsymbol{\varphi} _2^ * (t) = {\boldsymbol{\Lambda} ^{ - 1}}\left( {2{\boldsymbol{M}_2}(t)\boldsymbol{\pi} (t) + {\boldsymbol{N}_2}(t)} \right){{\rm e}^{ - {r_0}\left( {T - t} \right)}}, \hfill \\ \end{gathered} \right. \end{equation}$
其中 ${\boldsymbol{M}_2}(t)$ ${\boldsymbol{N}_2}(t)$ $p_2^ * (t)$ $\boldsymbol{\varphi} _2^ * (t)$
(3.18) $\begin{equation} {V_2}\left( {t,x,\boldsymbol{\pi} } \right) = x{{\rm e}^{{r_0}\left( {T - t} \right)}} + {\boldsymbol{\pi} ^ \top }{\boldsymbol{M}_2}(t)\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }{\boldsymbol{N}_2}(t) + {H_2}(t), \end{equation}$
其中 ${H_2}(t)$
4 数值分析
本节首先在单位风险过程没有跳跃的情况下分析了市场相关系数 $\rho$ $\Lambda$ $\gamma = 0.5$ $\alpha = 0.8$ ${r_0} = 0.05$ $\mu = 0.2$ $t = 0$ $T = 1$ ${\sigma _S} = 0.2$ $c = 1.5$ ${\sigma _0} = 1$ .
4.1 不带跳跃
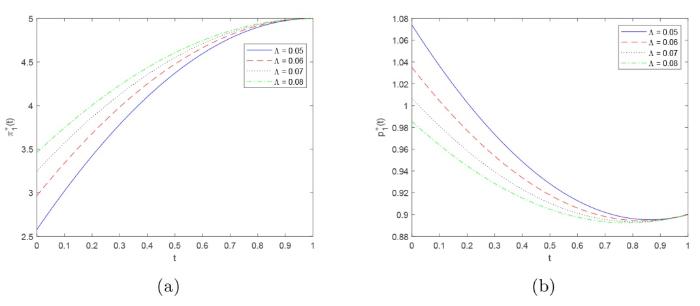
在推论 3.1 中, 我们得到了在不带跳跃的情况下, 保险公司投资份额 $\pi _1^ * (t)$ ${\pi _1}\left( T \right){\text{ = 5}}$ $\pi _1^ * (t)$
图1 描述了交易成本水平 $\Lambda$ 图1(a) 可以看出, 随着时间的推移, 保险公司对风险资产的投资逐渐增加, 而投资增长率逐渐降低. 在任意给定的时刻 $t$ $\pi _1^ * (t)$ $\Lambda$ 图1(b) 显示对于任意给定的时刻 $t$ $p_1^ * (t)$ $t$ $\pi _1^ * (t)$
图1
图1
交易成本水平 $\Lambda$ $\pi _1^ * (t)$ $p_1^ * (t)$
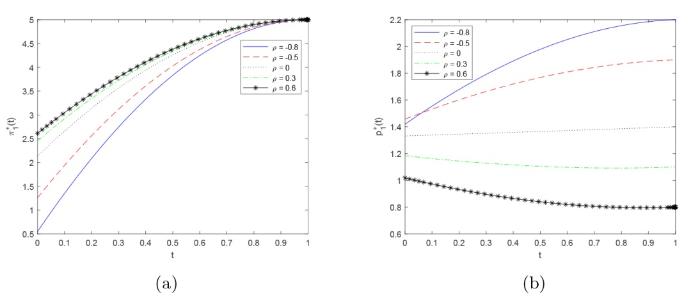
图2 展示了市场相关系数 $\rho$ 图2(a) 表明了对于任意给定的时刻 $t$ $\pi _1^ * (t)$ $\rho$ 9 ] 中的结果是一致的. 如图2(b) 所示, 当 $\rho < 0$ $p_1^ * (t)$ $\rho > 0$ $p_1^ * (t)$ $\rho = -0.5$ $\rho = -0.8$ $t_1$ . 当 $t < t_1$ $\rho = -0.5$ $\rho = -0.8$ $t > t_1$ $T - t=1$ $t=0$ ) 时文献 [9 ] 的结果表明, 最优风险控制策略随相关系数的增大先递减再递增. 而在本文中, 由图2(b) 可知, 在 $ t=0$ 9 ] 中的结果是相反的.
图2
图2
市场相关系数 $\rho$ $\pi _1^ * (t)$ $p_1^ * (t)$
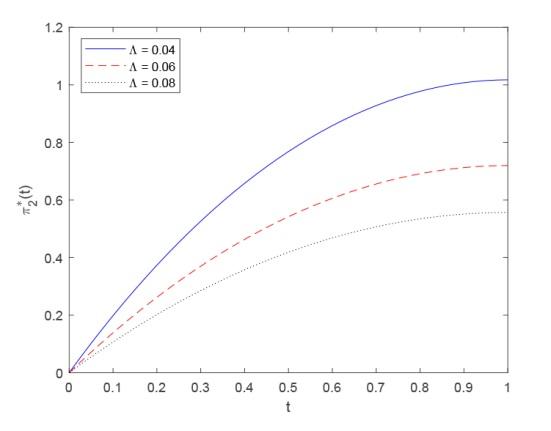
4.2 保险市场与金融市场独立
我们运用推论 3.2 中的结果进行数值模拟. 此时, 假设单位风险过程满足
(4.1) $\begin{equation} {\rm d}R(t) = \alpha {\rm d}t + {\sigma _0}{\rm d}{W_0}(t){\text{ + }}d\sum\limits_{i = 1}^{N(t)} {{Y_i}}, \end{equation}$
其中 ${\left\{ {N(t)} \right\}_{t > 0}}$ ${\lambda _0} > 0$ ${\left\{ {{Y_i}} \right\}_{i = 1,2,\cdots}}$ ${Y_i}$ ${\lambda _Y}$ ${\lambda _0}{ = }1$ ${\lambda _Y}{ = }1$ ${\pi _2}(0){ = 0}$ .
图3 描述了交易成本水平 $\Lambda$ 图3 可知, 在给定初始风险资产投资份额为 0 的情况下, 交易成本水平越高, 保险公司的投资增长率会越低. 这是因为较高的交易成本水平会导致保险公司的投资收益下降. 因此, 对于任意固定的时刻 $t$
图3
图3
交易成本水平 $\Lambda$ $\pi _2^ * (t)$
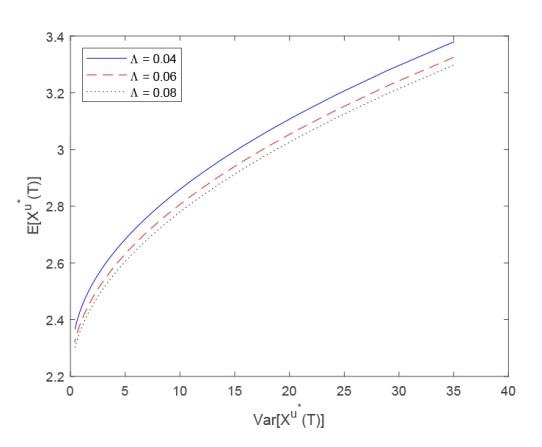
图4 展示了交易成本水平 $\Lambda$ 图4 中可以发现随着交易成本水平的增大, 有效前沿会降低. 这是因为交易成本水平越高, 保险公司的交易损失越大, 投资收益会随之降低. 因此, 当风险水平相同时, 交易成本水平越高, 保险公司获得的期望收益会越低. 也就是说, 当终端财富方差相同时, 交易成本水平越大, 终端财富期望值越小.
图4
图4
交易成本水平 $\Lambda$
5 结论
该文将交易成本和市场相关性同时引入到保险公司的最优风险控制与投资问题中. 在动态均值-方差优化目标下, 运用扩展的 HJB 方程进行求解, 并在特殊情况下给出了均衡策略和相应值函数的显式表达式. 最后通过数值算例分别在单位风险过程没有跳跃和无市场相关性这两种情况下进行了灵敏性分析. 结果表明, 随着交易成本水平和市场相关系数的增加, 由于交易损失和系统风险的增大, 资产增速会放缓. 而且, 当风险水平相同时, 交易成本水平越高, 保险公司获得的期望收益会越低.
本文中参数均假设为确定性函数或常数, 考虑到背景风险, 在后续研究中, 可以研究更一般的随机参数情形, 比如随机利率, 随机波动率等. 此外, 在实际中进行投资时往往会有各种限制, 比如卖空限制, 所以后续也可以考虑带投资限制的情况.
附录
A.1 定理 3.2 的证明
首先我们不考虑风险控制策略的非负限制, 经过计算后, (3.2) 式可以重写为
(A1) $\begin{equation}\label{rehjbequ} \begin{gathered} \mathop {\sup }\limits_{u \in \Pi } \left\{ {{V_t} + \left[ {{r_0}x + \left( {c - \alpha } \right)p + {\boldsymbol{\pi} ^ \top }\boldsymbol{\mu} - \frac{1}{2}{\boldsymbol{\varphi} ^ \top }\boldsymbol{\Lambda} \boldsymbol{\varphi} } \right]{V_x}} \right. + \boldsymbol{V}_\pi ^ \top \boldsymbol{\varphi} \hfill \\ + \frac{1}{2}\left( {{{\left( {{\boldsymbol{\pi} ^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}} - p{\sigma _0}} \right)}^2} + {\boldsymbol{\pi} ^ \top }{\boldsymbol{\sigma} _s}{{\boldsymbol{\hat \rho} }^2}\boldsymbol{\sigma} _s^ \top \boldsymbol{\pi} } \right)\left( {{V_{xx}} - \gamma g_x^2} \right) \hfill \\ + \left. {\int_0^\infty {\left( {V\left( {t,x - py,\boldsymbol{\pi} } \right) - V\left( {t,x,\boldsymbol{\pi} } \right) - \frac{\gamma }{2}{{\left( {g\left( {t,x - py,\boldsymbol{\pi} } \right) - g\left( {t,x,\boldsymbol{\pi} } \right)} \right)}^2}} \right)v\left( {{\rm d}y} \right)} } \right\} = 0. \hfill \\ \end{gathered} \end{equation}$
对 (A1) 式关于 $p$ $\boldsymbol{\varphi} $ $u(t){=}\left( {p(t),\boldsymbol{\varphi} (t)} \right)$
(A2) $\begin{equation}\label{supp} \begin{gathered} \left( {c - \alpha } \right){V_x} - {\sigma _0}\left( {{\boldsymbol{\pi} ^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}} - p{\sigma _0}} \right)\left( {{V_{xx}} - \gamma g_x^2} \right) \hfill \\ + \int_0^\infty {\left[ { - y{V_x}\left( {t,x - py,\boldsymbol{\pi} } \right) + \gamma y\left( {g\left( {t,x - py,\boldsymbol{\pi} } \right) - g\left( {t,x,\boldsymbol{\pi} } \right)} \right){g_x}\left( {t,x - py,\boldsymbol{\pi} } \right)} \right]v\left( {{\rm d}y} \right) = 0}, \hfill \\ \end{gathered} \end{equation}$
(A3) $\begin{equation}\label{supphi} \boldsymbol{\varphi} = {\boldsymbol{\Lambda} ^{ - 1}}\frac{{{\boldsymbol{V}_\pi }}}{{{V_x}}}. \end{equation}$
假设 $V\left( {t,x,\boldsymbol{\pi} } \right)$ $g\left( {t,x,\boldsymbol{\pi} } \right)$
(A4) $\begin{equation}\label{vandg} \left\{ \begin{gathered} V\left( {t,x,\boldsymbol{\pi} } \right) = A(t)x + {\boldsymbol{\pi} ^ \top }\boldsymbol{M}(t)\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }\boldsymbol{N}(t) + H(t), \hfill \\ g\left( {t,x,\boldsymbol{\pi} } \right) = a(t)x + {\boldsymbol{\pi} ^ \top }\boldsymbol{m}(t)\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }\boldsymbol{n}(t) + h(t). \hfill \\ \end{gathered} \right. \end{equation}$
把 (A4) 式代入 (A2) 与 (A3) 式中得到
(A5) $\begin{equation}\label{suppvg} \begin{gathered} \left( {c - \alpha } \right)A + \gamma {\sigma _0}\left( {{\boldsymbol{\pi} ^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}} - p{\sigma _0}} \right){a^2} - \int_0^\infty {\left( {yA + \gamma p{y^2}{a^2}} \right)v\left( {{\rm d}y} \right) = 0}, \end{gathered} \end{equation}$
(A6) $\begin{equation}\label{supphivg} \boldsymbol{\varphi} = {\boldsymbol{\Lambda} ^{ - 1}}\left( {2\boldsymbol{M}\boldsymbol{\pi} + \boldsymbol{N}} \right){A^{ - 1}}. \end{equation}$
把 (A4), (A5), (A6) 式代入 (A1) 式中得到
(A7) $\begin{equation} \begin{gathered} A'x + {\boldsymbol{\pi} ^ \top }\boldsymbol{M}'\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }\boldsymbol{N}' + H' + \left[ {{r_0}x + \left( {c - \alpha } \right)p + {\boldsymbol{\pi} ^ \top }\boldsymbol{\mu} } \right]A \hfill \\ {+}\frac{1}{{2A}}{\left( {2\boldsymbol{M}\boldsymbol{\pi} + \boldsymbol{N}} \right)^ \top }{\boldsymbol{\Lambda} ^{ - 1}}\left( {2\boldsymbol{M}\boldsymbol{\pi} + \boldsymbol{N}} \right) - \frac{\gamma }{2}\left[ {{{\left( {{\boldsymbol{\pi} ^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}} - {p^ * }{\sigma _0}} \right)}^2} + {\boldsymbol{\pi} ^ \top }{\boldsymbol{\sigma} _s}{{\boldsymbol{\hat \rho} }^2}\boldsymbol{\sigma} _s^ \top \boldsymbol{\pi} } \right]{a^2} \hfill \\ - \int_0^\infty {\left( {Apy + \frac{\gamma }{2}{a^2}{p^2}{y^2}} \right)v\left( {{\rm d}y} \right)} = 0. \hfill \\ \end{gathered} \end{equation}$
类似地, 把 (A4), (A5), (A6) 式代入 (3.4) 式中得到
(A8) $\begin{array}{l} a^{\prime} x+\pi^{\top} m^{\prime} \pi+\pi^{\top} n^{\prime}+h^{\prime} \\ +\left[r_{0} x+(c-\alpha) p+\pi^{\top} \mu-\frac{1}{2 A^{2}}(2 M \pi+N)^{\top} \Lambda^{-1}(2 M \pi+N)\right] a \\ +\frac{1}{A}(2 m \pi+n)^{\top} \Lambda^{-1}(2 M \pi+N)-\int_{0}^{\infty} a p y v(\mathrm{~d} y)=0. \end{array}$
(A9) $\begin{equation}\label{Aanda} \left\{ \begin{gathered} A{(t)^\prime } + {r_0}A(t) = a{(t)^\prime } + {r_0}a(t) = 0, \hfill \\ A\left( T \right) = a\left( T \right) = 1, \hfill \\ \end{gathered} \right. \end{equation}$
(A10) $\begin{equation}\label{Mdiff} \left\{ \begin{gathered} \boldsymbol{M}' + 2{A^{ - 1}}\boldsymbol{M}{\boldsymbol{\Lambda} ^{ - 1}}\boldsymbol{M} - \frac{\gamma }{2}{a^2}\left( {{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}{\boldsymbol{I}_{1 \times n}}\boldsymbol{\rho} \boldsymbol{\sigma} _s^ \top + {\boldsymbol{\sigma} _s}{{\boldsymbol{\hat \rho} }^2}\boldsymbol{\sigma} _s^ \top } \right) = {\boldsymbol{0}_{n \times n}}, \hfill \\ \boldsymbol{M}\left( T \right) = {\boldsymbol{0}_{n \times n}}, \hfill \\ \end{gathered} \right. \end{equation}$
(A11) $\begin{equation}\label{Ndiff} \left\{ \begin{gathered} \boldsymbol{N}' + 2{A^{ - 1}}\boldsymbol{M}{\boldsymbol{\Lambda} ^{ - 1}}\boldsymbol{N} + \boldsymbol{\mu} A + \gamma {a^2}p{\sigma _0}{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}} = {\boldsymbol{0}_{n \times 1}}, \hfill \\ \boldsymbol{N}\left( T \right) = {\boldsymbol{0}_{n \times 1}}, \hfill \\ \end{gathered} \right. \end{equation}$
(A12) $\begin{equation}\label{Hdiff} \left\{ \begin{gathered} H' + A\left( {c - \alpha } \right)p + \frac{1}{{2A}}{\boldsymbol{N}^ \top }{\boldsymbol{\Lambda} ^{ - 1}}\boldsymbol{N} - \frac{\gamma }{2}{a^2}{\left( {p{\sigma _0}} \right)^2} \hfill \\ - \int_0^\infty {\left( {Apy + \frac{\gamma }{2}{a^2}{p^2}{y^2}} \right)v\left( {{\rm d}y} \right)} = 0, \hfill \\ H\left( T \right) = 0, \hfill \\ \end{gathered} \right. \end{equation}$
(A13) $\begin{equation}\label{mdiff} \left\{ \begin{gathered} \boldsymbol{m}' + 4{A^{ - 1}}\boldsymbol{m}{\boldsymbol{\Lambda} ^{ - 1}}\boldsymbol{M} - 2\frac{a}{{{A^2}}}\boldsymbol{M}{\boldsymbol{\Lambda} ^{ - 1}}\boldsymbol{M} = {\boldsymbol{0}_{n \times n}}, \hfill \\ \boldsymbol{m}\left( T \right) = {\boldsymbol{0}_{n \times n}}, \hfill \\ \end{gathered} \right. \end{equation}$
(A14) $\begin{equation}\label{ndiff} \left\{ \begin{gathered} \boldsymbol{n}' + 2{A^{ - 1}}\boldsymbol{M}{\boldsymbol{\Lambda} ^{ - 1}}\boldsymbol{n} + 2{A^{ - 1}}\boldsymbol{m}{\boldsymbol{\Lambda} ^{ - 1}}\boldsymbol{N} + a\boldsymbol{\mu} - 2\frac{a}{{{A^2}}}\boldsymbol{M}{\boldsymbol{\Lambda} ^{ - 1}}\boldsymbol{N} = {\boldsymbol{0}_{n \times 1}}, \hfill \\ \boldsymbol{n}\left( T \right) = {\boldsymbol{0}_{n \times 1}}, \hfill \\ \end{gathered} \right. \end{equation}$
(A15) $\begin{equation}\label{hdiff} \left\{ \begin{gathered} h'{ + }a\left( {\left( {c - \alpha } \right)p - \frac{1}{{2{A^2}}}{\boldsymbol{N}^ \top }{\boldsymbol{\Lambda} ^{ - 1}}\boldsymbol{N}} \right) + \frac{1}{A}{\boldsymbol{n}^ \top }{\boldsymbol{\Lambda} ^{ - 1}}\boldsymbol{N} - \int_0^\infty {apyv\left( {{\rm d}y} \right)} = 0, \hfill \\ h\left( T \right) = 0. \hfill \\ \end{gathered} \right. \end{equation}$
进一步, 如果我们考虑风险控制策略的非负约束, 则由 (A1) 式易知均衡风险控制策略为 ${p^ * }(t) = p(t) \vee 0$ . 此时均衡投资策略为
(A16) $\begin{equation} V\left( {t,x,\boldsymbol{\pi} } \right) = x{{\rm e}^{{r_0}\left( {T - t} \right)}} + {\boldsymbol{\pi} ^ \top }\boldsymbol{M}(t)\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }\boldsymbol{\bar N}(t) + \bar H(t), \end{equation}$
这里的 $\boldsymbol{\bar N}(t)$ $\bar H(t)$ $p$ $p(t) \vee 0$ ). 且
$\boldsymbol{\bar n}(t)$ $\bar h(t)$ $p$ $p(t) \vee 0$ ).
A.2 推论 3.1 的证明
(A17) $\begin{equation} {\rm d}R(t) = c{\rm d}t + {\sigma _0}{\rm d}{W_0}(t). \end{equation}$
首先我们不考虑风险控制策略的非负约束, 由定理 3.2 可得均衡策略 ${u_1} = \left( {{p_1}(t),{\boldsymbol{\varphi} _1}(t)} \right)^ \top$
(A18) $\begin{equation}\label{u1} \left\{ \begin{gathered} {p_1}(t) = \frac{{\left( {c - \alpha } \right){{\rm e}^{ - {r_0}\left( {T - t} \right)}} + \gamma {\sigma _0}{\boldsymbol{\pi} ^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{\boldsymbol{n} \times 1}}}}{{\gamma \sigma _0^2}}, \hfill \\ {\boldsymbol{\varphi} _1}(t) = {\boldsymbol{\Lambda} ^{ - 1}}\left( {2{\boldsymbol{M}_1}(t)\boldsymbol{\pi} + {\boldsymbol{N}_1}(t)} \right){{\rm e}^{ - {r_0}\left( {T - t} \right)}}. \hfill \\ \end{gathered} \right. \end{equation}$
相应的值函数 ${V_1}\left( {t,x,\boldsymbol{\pi} } \right)$
(A19) $\begin{equation} {V_1}\left( {t,x,\boldsymbol{\pi} } \right) = x{{\rm e}^{{r_0}\left( {T - t} \right)}} + {\boldsymbol{\pi} ^ \top }{\boldsymbol{M}_1}(t)\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }{\boldsymbol{N}_1}(t) + {H_1}(t), \end{equation}$
其中 ${\boldsymbol{M}_1}(t)$ ${\boldsymbol{N}_1}(t)$ ${H_1}(t)$
(A20) $\begin{equation}\label{M1diff} \left\{ \begin{gathered} {\boldsymbol{M}_1^\prime} + 2{\boldsymbol{M}_1}{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{M}_1}{{\rm e}^{ - {r_0}\left( {T - t} \right)}} - \frac{\gamma }{2}{{\rm e}^{2{r_0}\left( {T - t} \right)}}\left( {{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}{\boldsymbol{I}_{1 \times n}}\boldsymbol{\rho} \boldsymbol{\sigma} _s^ \top + {\boldsymbol{\sigma} _s}{{\boldsymbol{\hat \rho} }^2}\boldsymbol{\sigma} _s^ \top } \right) = {\boldsymbol{0}_{n \times n}}, \hfill \\ {\boldsymbol{M}_1}\left( T \right) = {\boldsymbol{0}_{n \times n}}, \hfill \\ \end{gathered} \right. \end{equation}$
(A21) $\begin{equation}\label{N1diff} \left\{ \begin{gathered} {\boldsymbol{N}_1^\prime} + 2{\boldsymbol{M}_1}{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{N}_1}{{\rm e}^{ - {r_0}\left( {T - t} \right)}} + \boldsymbol{\mu} {{\rm e}^{{r_0}\left( {T - t} \right)}} + \gamma {p_1}{\sigma _0}{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}{{\rm e}^{2{r_0}\left( {T - t} \right)}} = {\boldsymbol{0}_{n \times 1}}, \hfill \\ {\boldsymbol{N}_1}\left( T \right) = {\boldsymbol{0}_{n \times 1}}, \hfill \\ \end{gathered} \right. \end{equation}$
(A22) $\begin{equation}\label{H1diff} \left\{ \begin{gathered} {H_1^\prime} + \left( {c - \alpha } \right){p_1}{{\rm e}^{{r_0}\left( {T - t} \right)}} + \frac{1}{2}\boldsymbol{N}_1^ \top {\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{N}_1}{{\rm e}^{ - {r_0}\left( {T - t} \right)}} - \frac{1}{2}\gamma {\left( {{p_1}{\sigma _0}} \right)^2}{{\rm e}^{2{r_0}\left( {T - t} \right)}} = 0, \hfill \\ {H_1}\left( T \right) = 0. \hfill \\ \end{gathered} \right. \end{equation}$
(A23) $\begin{equation}\label{N1exp} {\boldsymbol{N}_1}(t) = \int_t^T {{{\rm e}^{\int_t^s {2{{\rm e}^{ - {r_0}\left( {T - u} \right)}}{\boldsymbol{M}_1}\left( u \right){\boldsymbol{\Lambda} ^{ - 1}}{\rm d}u} }}\left( {\boldsymbol{\mu} {{\rm e}^{{r_0}\left( {T - s} \right)}} - \gamma {p_1}(s){\sigma _0}{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}{{\rm e}^{2{r_0}\left( {T - s} \right)}}} \right){\rm d}s}. \end{equation}$
注意到 ${\boldsymbol{\varphi} _1}(t) = \frac{{{\rm d}{\boldsymbol{\pi} _1}(t)}}{{{\rm d}t}}$
(A24) $\begin{equation}\label{pi1exp} {\boldsymbol{\pi} _1}(t) = {{\rm e}^{\int_0^t {\boldsymbol{k}(s){\rm d}s} }}\left( {\boldsymbol{\pi}_1 (0) + \int_0^t {{{\rm e}^{ - \int_0^s {\boldsymbol{k}\left( u \right){\rm d}u} }}{{\rm e}^{ - {r_0}\left( {T - s} \right)}}{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{N}_1}(s){\rm d}s} } \right), \end{equation}$
其中 $\boldsymbol{k}(s) = 2{{\rm e}^{ - {r_0}\left( {T - s} \right)}}{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{M}_1}(s)$ .
将 (A18) 式中 ${p_1}(t)$
(A25) $\begin{equation}\label{N1exp1} \begin{split} {\boldsymbol{N}_1}(t) &= \int_t^T {{{\rm e}^{\int_t^s {2{{\rm e}^{ - {r_0}\left( {T - u} \right)}}{\boldsymbol{M}_1}\left( u \right){\boldsymbol{\Lambda} ^{ - 1}}{\rm d}u} }}\left( {\boldsymbol{\mu} {{\rm e}^{{r_0}\left( {T - s} \right)}}} \right.} \hfill \\ & + \left. {{{\rm e}^{2{r_0}\left( {T - s} \right)}}\sigma _0^{ - 1}\left( {\left( {c - \alpha } \right){{\rm e}^{ - {r_0}\left( {T - s} \right)}} + \gamma {\sigma _0}{\boldsymbol{\pi} _1}{{(s)}^ \top }{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}} \right){\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}} \right){\rm d}s. \hfill \\ \end{split} \end{equation}$
(A26) $\begin{equation}\label{pi1exp1} {\boldsymbol{\pi} _1}(t) = {{\rm e}^{\int_0^t {\boldsymbol{k}(s){\rm d}s} }} \bigg( {{\boldsymbol{\pi} _1}(0)} + {\int_0^t {{{\rm e}^{ - \int_0^s {\boldsymbol{k}\left( u \right){\rm d}u} }}{{\rm e}^{ - {r_0}\left( {T - s} \right)}}{\boldsymbol{\Lambda} ^{ - 1}}\int_s^T {{{\rm e}^{\int_s^u {2{{\rm e}^{ - {r_0}\left( {T - v} \right)}}{\boldsymbol{M}_1}\left( v \right){\boldsymbol{\Lambda} ^{ - 1}}{\rm d}v} }}} \boldsymbol{l}\left( u \right){\rm d}u{\rm d}s} } \bigg), \end{equation}$
其中 $\boldsymbol{l}\left( u \right) = \boldsymbol{\mu} {{\rm e}^{{r_0}\left( {T - u} \right)}} + \left( {c - \alpha } \right)\sigma _0^{ - 1}{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}{{\rm e}^{{r_0}\left( {T - u} \right)}} + \gamma {\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}{\boldsymbol{I}_{1 \times n}}\boldsymbol{\rho} \boldsymbol{\sigma} _s^ \top {\boldsymbol{\pi} _1}\left( u \right){{\rm e}^{2{r_0}\left( {T - u} \right)}}$ .
(A27) $\begin{equation}\label{pi1d1} \begin{split} {\boldsymbol{\pi} _1}(t) &= {{\rm e}^{\int_0^t {\boldsymbol{k}(s){\rm d}s} }}\left( {{\boldsymbol{\pi} _1}(0)} \right. \hfill \\ & + \int_0^t {\left( {\int_0^u {{{\rm e}^{ - \int_0^s {\boldsymbol{k}\left( u \right){\rm d}u} }}{{\rm e}^{ - {r_0}\left( {T - s} \right)}}{\boldsymbol{\Lambda} ^{ - 1}}{{\rm e}^{\int_s^u {2{{\rm e}^{ - {r_0}\left( {T - v} \right)}}{\boldsymbol{M}_1}\left( v \right){\boldsymbol{\Lambda} ^{ - 1}}{\rm d}v} }}\boldsymbol{l}\left( u \right){\rm d}s} } \right){\rm d}u} \hfill \\ & + \left. {\int_t^T {\left( {\int_0^t {{{\rm e}^{ - \int_0^s {\boldsymbol{k}\left( u \right){\rm d}u} }}{{\rm e}^{ - {r_0}\left( {T - s} \right)}}{\boldsymbol{\Lambda} ^{ - 1}}{{\rm e}^{\int_s^u {2{{\rm e}^{ - {r_0}\left( {T - v} \right)}}{\boldsymbol{M}_1}\left( v \right){\boldsymbol{\Lambda} ^{ - 1}}{\rm d}v} }}\boldsymbol{l}\left( u \right){\rm d}s} } \right){\rm d}u} } \right). \hfill \\ \end{split} \end{equation}$
对 (A27) 式左乘 ${{\rm e}^{ - \int_0^t {\boldsymbol{k}(s){\rm d}s} }}$ $t$ ${\boldsymbol{\pi} _1}(t) $
(A28) $\begin{equation} \begin{gathered} {\boldsymbol{\pi} _1}{(t)^{\prime \prime }} + \left( {2{{\rm e}^{ - {r_0}\left( {T - t} \right)}}{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{M}_1}(t) - {r_0}{\boldsymbol{E}_{n \times n}} - \boldsymbol{k}(t)} \right){\boldsymbol{\pi} _1}{(t)^\prime } \hfill \\ + \left( {\gamma {\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}{\boldsymbol{I}_{1 \times n}}\boldsymbol{\rho} \boldsymbol{\sigma} _s^ \top {{\rm e}^{{r_0}\left( {T - t} \right)}} - \boldsymbol{k}{{(t)}^\prime } - 2{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{M}_1}\left( v \right)\boldsymbol{k}(t){{\rm e}^{ - {r_0}\left( {T - t} \right)}} + {r_0}\boldsymbol{k}(t)} \right){\boldsymbol{\pi} _1}(t) \hfill \\ + {\boldsymbol{\Lambda} ^{ - 1}}\left( {\boldsymbol{\mu} + \left( {c - \alpha } \right)\sigma _0^{ - 1}{\boldsymbol{\sigma} _s}\boldsymbol{\rho} {\boldsymbol{I}_{n \times 1}}} \right) = {\boldsymbol{0}_{n \times 1}}. \hfill \\ \end{gathered} \end{equation}$
进一步, 如果我们考虑风险控制策略的非负约束, 则由定理 3.2, 均衡策略 $u_1^ * (t) = \left( {p_1^ * (t),\boldsymbol{\varphi} _1^ * (t)} \right)^ \top$ ${V_1}\left( {t,x,\boldsymbol{\pi} } \right)$ ${\boldsymbol{\bar N}_1}(t)$ ${\bar H_1}(t)$ ${p_1}(t)$ $p_1^ * (t)$ ) , 而投资份额 $\boldsymbol{\pi} _1^ * (t)$
A.3 推论 3.2 的证明
由定理 3.2, 均衡策略 $u_2^ * (t) = \left( {p_2^ * (t),\boldsymbol{\varphi} _2^ * (t)} \right)^ \top$
(A29) $\begin{equation} \left\{ \begin{gathered} \left( {c - \alpha } \right){{\rm e}^{{r_0}\left( {T - t} \right)}} - \gamma \sigma _0^2p_2^ * (t){{\rm e}^{2{r_0}\left( {T - t} \right)}} \hfill \\ - \int_0^\infty {\left( {y{{\rm e}^{{r_0}\left( {T - t} \right)}} + \gamma p_2^ * (t){y^2}{{\rm e}^{2{r_0}\left( {T - t} \right)}}} \right)v\left( {{\rm d}y} \right)} = 0, \hfill \\ \boldsymbol{\varphi} _2^ * (t) = {\boldsymbol{\Lambda} ^{ - 1}}\left( {2{\boldsymbol{M}_2}(t)\boldsymbol{\pi} (t) + {\boldsymbol{N}_2}(t)} \right){{\rm e}^{ - {r_0}\left( {T - t} \right)}}. \hfill \\ \end{gathered} \right. \end{equation}$
则由 $\boldsymbol{\varphi} _2^ * (t) = \frac{{{\rm d}\boldsymbol{\pi} _2^ * (t)}}{{{\rm d}t}}$ $\boldsymbol{\pi} _2^ * (t)$
相应的均衡值函数 ${V_2}\left( {t,x,\boldsymbol{\pi} } \right)$
(A30) $\begin{equation} {V_2}\left( {t,x,\boldsymbol{\pi} } \right) = x{{\rm e}^{{r_0}\left( {T - t} \right)}} + {\boldsymbol{\pi} ^ \top }{\boldsymbol{M}_2}(t)\boldsymbol{\pi} + {\boldsymbol{\pi} ^ \top }{\boldsymbol{N}_2}(t) + {H_2}(t), \end{equation}$
其中 ${\boldsymbol{M}_2}(t)$ ${\boldsymbol{N}_2}(t)$ ${H_2}(t)$
(A31) $\begin{equation}\label{M2diff} \left\{ \begin{gathered} {\boldsymbol{M}_2^\prime} + 2{\boldsymbol{M}_2}{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{M}_2}{{\rm e}^{ - {r_0}\left( {T - t} \right)}} - \frac{\gamma }{2}{\boldsymbol{\sigma} _s}\boldsymbol{\sigma} _s^ \top {{\rm e}^{2{r_0}\left( {T - t} \right)}} = {\boldsymbol{0}_{n \times n}}, \hfill \\ {\boldsymbol{M}_2}\left( T \right) = {\boldsymbol{0}_{n \times n}}, \hfill \\ \end{gathered} \right. \end{equation}$
(A32) $\begin{equation}\label{N2diff} \left\{ \begin{gathered} {\boldsymbol{N}_2^\prime} + 2{\boldsymbol{M}_2}{\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{N}_2}{{\rm e}^{ - {r_0}\left( {T - t} \right)}} + \boldsymbol{\mu} {{\rm e}^{ {r_0}\left( {T - t} \right)}} = {\boldsymbol{0}_{n \times 1}}, \hfill \\ {\boldsymbol{N}_2}\left( T \right) = {\boldsymbol{0}_{n \times 1}}, \hfill \\ \end{gathered} \right. \end{equation}$
(A33) $\begin{equation}\label{H2diff} \left\{ \begin{gathered} {H_2^\prime} + \left( {c - \alpha } \right)p_2^ * {{\rm e}^{{r_0}\left( {T - t} \right)}} + \frac{1}{2}{\boldsymbol{N}_2}^ \top {\boldsymbol{\Lambda} ^{ - 1}}{\boldsymbol{N}_2}{{\rm e}^{ - {r_0}\left( {T - t} \right)}} - \frac{\gamma }{2}{\left( {p_2^ * {\sigma _0}} \right)^2}{{\rm e}^{2{r_0}\left( {T - t} \right)}} \hfill \\ - \int_0^\infty {\left( {p_2^ * y{{\rm e}^{{r_0}\left( {T - t} \right)}} + \frac{\gamma }{2}{{\left( {p_2^ * } \right)}^2}{y^2}{{\rm e}^{2{r_0}\left( {T - t} \right)}}} \right)v\left( {{\rm d}y} \right)} = 0, \hfill \\ {H_2}\left( T \right) = 0. \hfill \\ \end{gathered} \right. \end{equation}$
对任意固定的 $t \in \left[ {0,T} \right]$
(A34) $\begin{equation}\label{f1p} {f_1}\left( p \right): = \left( {c - \alpha } \right){{\rm e}^{{r_0}\left( {T - t} \right)}} - \gamma p\sigma _0^2{{\rm e}^{2{r_0}\left( {T - t} \right)}} - \int_0^\infty {\left( {y{{\rm e}^{{r_0}\left( {T - t} \right)}} + \gamma p{y^2}{{\rm e}^{2{r_0}\left( {T - t} \right)}}} \right)v\left( {{\rm d}y} \right)}, \end{equation}$
(A35) $\begin{equation} \frac{{\partial {f_1}\left( p \right)}}{{\partial p}} = - \gamma \sigma _0^2{{\rm e}^{2{r_0}\left( {T - t} \right)}} - \int_0^\infty {\gamma {y^2}{{\rm e}^{2{r_0}\left( {T - t} \right)}}v\left( {{\rm d}y} \right)} < 0. \end{equation}$
因此, 由连续函数的介值定理知方程 ${f_1}\left( p \right) = 0$
参考文献
View Option
[1]
Bai L Guo J Optimal proportional reinsurance and investment with multiple risky assets and no-shorting constraint
Insurance: Mathematics and Economics , 2008 , 42 3 ): 968 -975
DOI:10.1016/j.insmatheco.2007.11.002
URL
[本文引用: 1]
[2]
Zeng Y Li Z Optimal time-consistent investment and reinsurance policies for mean-variance insurers
Insurance: Mathematics and Economics , 2011 , 49 1 ): 145 -154
[本文引用: 1]
[3]
季锟鹏 , 彭幸春 . 考虑通胀风险与最低绩效保障的损失厌恶型保险公司的最优投资与再保险策略
数学物理学报 , 2022 , 42A 4 ): 1265 -1280
[本文引用: 1]
Ji K Peng X Optimal investment and reinsurance strategies for loss-averse insurer considering inflation risk and minimum performance guarantee
Acta Mathematica Sci , 2022 , 42A 4 ): 1265 -1280
[本文引用: 1]
[4]
黄玲 , 刘海燕 , 陈密 . 基于 Ornstein-Uhlenbeck 过程下具有两个再保险公司的比例再保险与投资
数学物理学报 , 2023 , 43A 3 ): 957 -969
[本文引用: 1]
Huang L Liu H Chen M Proportion reinsurance and investment based on the Ornstein-Uhlenbeck process in the presence of two reinsurers
Acta Mathematica Sci , 2023 , 43A 3 ): 957 -969
[本文引用: 1]
[5]
Zou B Cadenillas A Optimal investment and risk control policies for an insurer: Expected utility maximization
Insurance: Mathematics and Economics , 2014 , 58 57 -67
[本文引用: 2]
[6]
Peng X Wang W Optimal investment and risk control for an insurer under inside information
Insurance: Mathematics and Economics , 2016 , 69 104 -116
[本文引用: 1]
[7]
Bo L Wang S Optimal investment and risk control for an insurer with stochastic factor
Operations Research Letters , 2017 , 45 3 ): 259 -265
[本文引用: 1]
[8]
Peng X Chen F Wang W Optimal investment and risk control for an insurer with partial information in an anticipating environment
Scandinavian Actuarial Journal , 2018 , 2018 10 ): 933 -952
[本文引用: 1]
[9]
Shen Y Zou B Mean-variance investment and risk control strategies-A time-consistent approach via a forward auxiliary process
Insurance: Mathematics and Economics , 2021 , 97 68 -80
[本文引用: 4]
[10]
Chen F Li B Peng X Portfolio Selection and Risk Control for an Insurer With Uncertain Time Horizon and Partial Information in an Anticipating Environment
Methodology and Computing in Applied Probability , 2022 , 24 2 ): 635 -659
[本文引用: 1]
[11]
Bai L Guo J Optimal dynamic excess-of-loss reinsurance and multidimensional portfolio selection
Science China Mathematics , 2010 , 53 1787 -1804
[本文引用: 1]
[12]
王雨薇 , 荣喜民 , 赵慧 . 基于模型不确定性的保险人最优投资再保险问题研究
工程数学学报 , 2022 , 39 1 ): 1 -19
[本文引用: 1]
Wang Y Rong X Zhao H Optimal reinsurance and investment strategies for insurers with ambiguity aversion: Minimizing the probability of ruin
Chinese Journal of Engineering Mathematics , 2022 , 39 1 ): 1 -19
[本文引用: 1]
[13]
Bayraktar E Zhang Y Minimizing the probability of lifetime ruin under ambiguity aversion
SIAM Journal on Control and Optimization , 2015 , 53 1 ): 58 -90
[本文引用: 1]
[14]
Bi J Meng Q Zhang Y Dynamic mean-variance and optimal reinsurance problems under the no-bankruptcy constraint for an insurer
Annals of Operations Research , 2014 , 212 43 -59
[本文引用: 1]
[15]
Sun Z Guo J Optimal mean-variance investment and reinsurance problem for an insurer with stochastic volatility
Mathematical Methods of Operations Research , 2018 , 88 59 -79
[本文引用: 1]
[16]
Wang T Wei J Mean-variance portfolio selection under a non-Markovian regime-switching model
Journal of Computational and Applied Mathematics , 2019 , 350 442 -455
[本文引用: 1]
[17]
Björk T Murgoci A A general theory of Markovian time inconsistent stochastic control problems
Ssrn Electronic Journal , 2010 , 18 3 ): 545 -592
[本文引用: 3]
[18]
Lin X Qian Y Time-consistent mean-variance reinsurance-investment strategy for insurers under CEV model
Scandinavian Actuarial Journal , 2016 , 2016 7 ): 646 -671
[本文引用: 2]
[19]
Björk T Murgoci A Zhou X Y Mean-variance portfolio optimization with state-dependent risk aversion. Mathematical Finance: An International Journal of Mathematics
Statistics and Financial Economics , 2014 , 24 1 ): 1 -24
[本文引用: 3]
[20]
Bi J Cai J Optimal investment-reinsurance strategies with state dependent risk aversion and VaR constraints in correlated markets
Insurance: Mathematics and Economics , 2019 , 85 1 -14
[本文引用: 2]
[21]
Yuan Y Han X Liang Z et al . Optimal reinsurance-investment strategy with thinning dependence and delay factors under mean-variance framework
European Journal of Operational Research , 2023 , 311 2 ): 581 -595
[本文引用: 2]
[22]
Yoshimoto A The mean-variance approach to portfolio optimization subject to transaction costs
Journal of the Operations Research Society of Japan , 1996 , 39 1 ): 99 -117
[本文引用: 1]
[23]
He L Liang Z Optimal financing and dividend control of the insurance company with fixed and proportional transaction costs
Insurance: Mathematics and Economics , 2009 , 44 1 ): 88 -94
[本文引用: 1]
[24]
Hobson D Tse A S L Zhu Y Optimal consumption and investment under transaction costs
Mathematical Finance , 2019 , 29 2 ): 483 -506
DOI:10.1111/mafi.12187
[本文引用: 1]
In this paper, we consider the Merton problem in a market with a single risky asset and proportional transaction costs. We give a complete solution of the problem up to the solution of a first-crossing problem for a first-order differential equation. We find that the characteristics of the solution (e.g., well-posedness) can be related to some simple properties of a univariate quadratic whose coefficients are functions of the parameters of the problem. Our solution to the problem via the value function includes expressions for the boundaries of the no-transaction wedge. Using these expressions, we prove a precise condition for when leverage occurs. One new and unexpected result is that when the solution to the Merton problem (without transaction costs) involves a leveraged position, and when transaction costs are large, the location of the boundary at which sales of the risky asset occur is independent of the transaction cost on purchases.
[25]
Mei X Nogales F J Portfolio selection with proportional transaction costs and predictability
Journal of Banking & Finance , 2018 , 94 131 -151
[本文引用: 1]
[26]
Melnyk Y Muhle-Karbe J Seifried F T Lifetime investment and consumption with recursive preferences and small transaction costs
Mathematical Finance , 2020 , 30 3 ): 1135 -1167
[本文引用: 1]
[27]
Gârleanu N Pedersen L H Dynamic trading with predictable returns and transaction costs
The Journal of Finance , 2013 , 68 6 ): 2309 -2340
[本文引用: 3]
[28]
Gârleanu N Pedersen L H Dynamic portfolio choice with frictions
Journal of Economic Theory , 2016 , 165 487 -516
[本文引用: 5]
[29]
Ma G Siu C C Zhu S P Dynamic portfolio choice with return predictability and transaction costs
European Journal of Operational Research , 2019 , 278 3 ): 976 -988
[本文引用: 4]
[30]
Bensoussan A Ma G Siu C C et al . Dynamic mean-variance problem with frictions
Finance and Stochastics , 2022 , 26 2 ): 267 -300
[本文引用: 2]
Optimal proportional reinsurance and investment with multiple risky assets and no-shorting constraint
1
2008
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
Optimal time-consistent investment and reinsurance policies for mean-variance insurers
1
2011
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
考虑通胀风险与最低绩效保障的损失厌恶型保险公司的最优投资与再保险策略
1
2022
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
考虑通胀风险与最低绩效保障的损失厌恶型保险公司的最优投资与再保险策略
1
2022
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
基于 Ornstein-Uhlenbeck 过程下具有两个再保险公司的比例再保险与投资
1
2023
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
基于 Ornstein-Uhlenbeck 过程下具有两个再保险公司的比例再保险与投资
1
2023
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
Optimal investment and risk control policies for an insurer: Expected utility maximization
2
2014
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
Optimal investment and risk control for an insurer under inside information
1
2016
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
Optimal investment and risk control for an insurer with stochastic factor
1
2017
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
Optimal investment and risk control for an insurer with partial information in an anticipating environment
1
2018
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
Mean-variance investment and risk control strategies-A time-consistent approach via a forward auxiliary process
4
2021
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
... 图2 展示了市场相关系数 $\rho$ 图2(a) 表明了对于任意给定的时刻 $t$ $\pi _1^ * (t)$ $\rho$ 9 ] 中的结果是一致的. 如图2(b) 所示, 当 $\rho < 0$ $p_1^ * (t)$ $\rho > 0$ $p_1^ * (t)$ $\rho = -0.5$ $\rho = -0.8$ $t_1$ . 当 $t < t_1$ $\rho = -0.5$ $\rho = -0.8$ $t > t_1$ $T - t=1$ $t=0$ ) 时文献 [9 ] 的结果表明, 最优风险控制策略随相关系数的增大先递减再递增. 而在本文中, 由图2(b) 可知, 在 $ t=0$ 9 ] 中的结果是相反的. ...
... ) 时文献 [9 ] 的结果表明, 最优风险控制策略随相关系数的增大先递减再递增. 而在本文中, 由图2(b) 可知, 在 $ t=0$ 9 ] 中的结果是相反的. ...
... 时, 均衡风险控制策略随相关系数的增大先递增再递减, 与文献 [9 ] 中的结果是相反的. ...
Portfolio Selection and Risk Control for an Insurer With Uncertain Time Horizon and Partial Information in an Anticipating Environment
1
2022
... 有关最优投资与再保险问题[1 ⇓ ⇓ -4 ] . 另一种方法是直接通过管理保单数量来控制保险风险. 例如, Zou 和 Cadenillas[5 ] 在期望效用最大化准则下研究了保险公司的最优投资和风险控制问题. Peng 和 Wang[6 ] 研究了具有市场内幕信息的保险公司的最优投资和风险控制问题. Bo 和 Wang[7 ] 引入随机因子, 研究了保险公司的最优风险控制和投资问题. Peng 等[8 ] 假设保险公司只拥有市场部分信息, 在对数效用最大化准则下求解了最优投资和风险控制策略. Shen 和 Zou[9 ] 通过引入前向辅助过程求解了时间一致的投资与风险控制策略. Chen 等[10 ] 在保险公司只拥有市场部分信息并且终端决策时刻不确定的情况下研究了保险公司的最优投资和风险控制问题. ...
Optimal dynamic excess-of-loss reinsurance and multidimensional portfolio selection
1
2010
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
基于模型不确定性的保险人最优投资再保险问题研究
1
2022
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
基于模型不确定性的保险人最优投资再保险问题研究
1
2022
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
Minimizing the probability of lifetime ruin under ambiguity aversion
1
2015
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
Dynamic mean-variance and optimal reinsurance problems under the no-bankruptcy constraint for an insurer
1
2014
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
Optimal mean-variance investment and reinsurance problem for an insurer with stochastic volatility
1
2018
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
Mean-variance portfolio selection under a non-Markovian regime-switching model
1
2019
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
A general theory of Markovian time inconsistent stochastic control problems
3
2010
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
... 由于 ${J^u}\left( {{t},x,\boldsymbol{\pi} } \right)$ ${\mathbb{E}_{t,x,\boldsymbol{\pi} }}\left[ {{X^u}\left( T \right)} \right]$ [17 ] 和 Björk 等[19 ] , 我们给出时间一致的均衡风险控制与投资策略的定义. ...
... 证 参见文献 [17 ], 此处从略. ...
Time-consistent mean-variance reinsurance-investment strategy for insurers under CEV model
2
2016
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
... 参考文献 [29 ], 考虑二次型交易成本, 该文研究动态均值-方差准则下保险公司的最优风险控制与投资问题. 假设金融市场由无风险资产和多种风险资产组成, 并且运用跳扩散过程来描述保险公司单位风险的动态模型. 与现有的均值-方差准则下的最优风险控制和投资问题的文献相比, 包括文献 [18 ⇓ ⇓ -21 ] 等, 本文将二次型交易成本纳入模型, 并且假设保险风险与金融风险存在相关性. 虽然 Garleanu 和 Pedersen[28 ] , Ma 等[29 ] 和 Bensoussan 等[30 ] 均考虑了二次型交易成本, 但是这些工作并没有考虑到保险风险控制以及保险风险与金融风险的相关性. 在博弈论框架下, 通过求解扩展的 HJB 方程组, 我们得到了依赖于矩阵 Riccati 方程组的解的均衡策略和相应的值函数. 此外, 还进一步研究了一些特殊情况, 并给出了均衡策略和值函数的更具体的表达式. 通过数值分析发现, 随着交易成本水平或相关系数的增加, 投资的增长率会减小. 并且交易成本水平的增加会导致更差的有效前沿. ...
Mean-variance portfolio optimization with state-dependent risk aversion. Mathematical Finance: An International Journal of Mathematics
3
2014
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
... 参考文献 [29 ], 考虑二次型交易成本, 该文研究动态均值-方差准则下保险公司的最优风险控制与投资问题. 假设金融市场由无风险资产和多种风险资产组成, 并且运用跳扩散过程来描述保险公司单位风险的动态模型. 与现有的均值-方差准则下的最优风险控制和投资问题的文献相比, 包括文献 [18 ⇓ ⇓ -21 ] 等, 本文将二次型交易成本纳入模型, 并且假设保险风险与金融风险存在相关性. 虽然 Garleanu 和 Pedersen[28 ] , Ma 等[29 ] 和 Bensoussan 等[30 ] 均考虑了二次型交易成本, 但是这些工作并没有考虑到保险风险控制以及保险风险与金融风险的相关性. 在博弈论框架下, 通过求解扩展的 HJB 方程组, 我们得到了依赖于矩阵 Riccati 方程组的解的均衡策略和相应的值函数. 此外, 还进一步研究了一些特殊情况, 并给出了均衡策略和值函数的更具体的表达式. 通过数值分析发现, 随着交易成本水平或相关系数的增加, 投资的增长率会减小. 并且交易成本水平的增加会导致更差的有效前沿. ...
... 由于 ${J^u}\left( {{t},x,\boldsymbol{\pi} } \right)$ ${\mathbb{E}_{t,x,\boldsymbol{\pi} }}\left[ {{X^u}\left( T \right)} \right]$ [17 ] 和 Björk 等[19 ] , 我们给出时间一致的均衡风险控制与投资策略的定义. ...
Optimal investment-reinsurance strategies with state dependent risk aversion and VaR constraints in correlated markets
2
2019
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
... 参考文献 [29 ], 考虑二次型交易成本, 该文研究动态均值-方差准则下保险公司的最优风险控制与投资问题. 假设金融市场由无风险资产和多种风险资产组成, 并且运用跳扩散过程来描述保险公司单位风险的动态模型. 与现有的均值-方差准则下的最优风险控制和投资问题的文献相比, 包括文献 [18 ⇓ ⇓ -21 ] 等, 本文将二次型交易成本纳入模型, 并且假设保险风险与金融风险存在相关性. 虽然 Garleanu 和 Pedersen[28 ] , Ma 等[29 ] 和 Bensoussan 等[30 ] 均考虑了二次型交易成本, 但是这些工作并没有考虑到保险风险控制以及保险风险与金融风险的相关性. 在博弈论框架下, 通过求解扩展的 HJB 方程组, 我们得到了依赖于矩阵 Riccati 方程组的解的均衡策略和相应的值函数. 此外, 还进一步研究了一些特殊情况, 并给出了均衡策略和值函数的更具体的表达式. 通过数值分析发现, 随着交易成本水平或相关系数的增加, 投资的增长率会减小. 并且交易成本水平的增加会导致更差的有效前沿. ...
Optimal reinsurance-investment strategy with thinning dependence and delay factors under mean-variance framework
2
2023
... 动态均值-方差准则是最优风险控制和投资问题研究中的常用优化准则, 相比较期望效用最大化准则[5 ,11 ] 和最小化破产概率准则[12 ,13 ] , 它能平衡保险公司的收益和风险. 然而, 动态均值-方差准则存在时间不一致问题, 这意味着当前的最优决策在未来并不一定是最优的. 主要有两种方法来应对时间不一致问题. 一种方法是寻求预先承诺的策略, 如 Bi 等[14 ] , Sun 和 Guo[15 ] , Wang 和 Wei[16 ] . 在预先承诺策略中, 决策者仅依赖于初始信息求解最优策略, 这意味着决策者在初始时刻选择了一个策略来最大化目标函数,然后沿用这个策略. 另一种方法是在博弈论框架下处理动态均值-方差问题, 寻找时间一致的均衡策略, 该策略不仅在当前是均衡的, 而且在未来的任何时刻都保持均衡性. 有关这种方法的更多细节, 可以参考 Björk 和 Murgoci[17 ] . 由于时间一致性对理性的决策者至关重要, 许多研究都采用了这种方法来克服动态均值- 方差问题的时间不一致性. Lin 和 Qian[18 ] 在均值-方差准则下将 CEV 模型纳入最优再保险和投资问题中, 得到了时间一致的再保险和投资策略的封闭表达式和相应的值函数. Björk 等[19 ] 假设决策者的风险厌恶与当前的财富值有关, 并在动态均值-方差准则下求解了时间一致的投资组合策略. Bi 和 Cai[20 ] 将状态依赖的风险规避和 VaR 约束引入到均值-方差再保险和投资问题中, 获得了时间一致的均衡策略. Yuan 等[21 ] 在均值-方差准则下研究了具有稀疏相依结构的风险模型的时间一致再保险与投资问题. ...
... 参考文献 [29 ], 考虑二次型交易成本, 该文研究动态均值-方差准则下保险公司的最优风险控制与投资问题. 假设金融市场由无风险资产和多种风险资产组成, 并且运用跳扩散过程来描述保险公司单位风险的动态模型. 与现有的均值-方差准则下的最优风险控制和投资问题的文献相比, 包括文献 [18 ⇓ ⇓ -21 ] 等, 本文将二次型交易成本纳入模型, 并且假设保险风险与金融风险存在相关性. 虽然 Garleanu 和 Pedersen[28 ] , Ma 等[29 ] 和 Bensoussan 等[30 ] 均考虑了二次型交易成本, 但是这些工作并没有考虑到保险风险控制以及保险风险与金融风险的相关性. 在博弈论框架下, 通过求解扩展的 HJB 方程组, 我们得到了依赖于矩阵 Riccati 方程组的解的均衡策略和相应的值函数. 此外, 还进一步研究了一些特殊情况, 并给出了均衡策略和值函数的更具体的表达式. 通过数值分析发现, 随着交易成本水平或相关系数的增加, 投资的增长率会减小. 并且交易成本水平的增加会导致更差的有效前沿. ...
The mean-variance approach to portfolio optimization subject to transaction costs
1
1996
... 以上所有的研究都假设市场是无摩擦的, 忽略了在金融市场中投资的交易成本. 然而, 在实际的投资交易中, 交易成本是不可避免的, 投资于风险资产时通常需要支付相应的交易费用, 这会一定程度上降低交易策略的收益. 因此, 不应忽视交易成本对投资绩效的影响. Yoshimoto[22 ] 研究了受交易成本影响的投资组合优化问题, 实证分析表明, 忽略交易成本会导致投资组合效率低下. He 和 Liang[23 ] 考虑金融市场中具有固定和比例交易成本, 研究了保险公司的最优融资和股利控制问题. Hobson 等[24 ] 求解了金融市场中具有比例交易成本和单一风险资产的默顿问题. Mei 和 Nogales[25 ] 假设金融市场中存在多个风险资产和比例交易成本, 在收益可预测的情况下研究了多阶段的投资组合选择问题. Melnyk 等[26 ] 探讨了在等弹性递归效用下, 具有小交易成本的终身消费和投资组合选择问题. Gârleanu 和 Pedersen[27 ] 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
Optimal financing and dividend control of the insurance company with fixed and proportional transaction costs
1
2009
... 以上所有的研究都假设市场是无摩擦的, 忽略了在金融市场中投资的交易成本. 然而, 在实际的投资交易中, 交易成本是不可避免的, 投资于风险资产时通常需要支付相应的交易费用, 这会一定程度上降低交易策略的收益. 因此, 不应忽视交易成本对投资绩效的影响. Yoshimoto[22 ] 研究了受交易成本影响的投资组合优化问题, 实证分析表明, 忽略交易成本会导致投资组合效率低下. He 和 Liang[23 ] 考虑金融市场中具有固定和比例交易成本, 研究了保险公司的最优融资和股利控制问题. Hobson 等[24 ] 求解了金融市场中具有比例交易成本和单一风险资产的默顿问题. Mei 和 Nogales[25 ] 假设金融市场中存在多个风险资产和比例交易成本, 在收益可预测的情况下研究了多阶段的投资组合选择问题. Melnyk 等[26 ] 探讨了在等弹性递归效用下, 具有小交易成本的终身消费和投资组合选择问题. Gârleanu 和 Pedersen[27 ] 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
Optimal consumption and investment under transaction costs
1
2019
... 以上所有的研究都假设市场是无摩擦的, 忽略了在金融市场中投资的交易成本. 然而, 在实际的投资交易中, 交易成本是不可避免的, 投资于风险资产时通常需要支付相应的交易费用, 这会一定程度上降低交易策略的收益. 因此, 不应忽视交易成本对投资绩效的影响. Yoshimoto[22 ] 研究了受交易成本影响的投资组合优化问题, 实证分析表明, 忽略交易成本会导致投资组合效率低下. He 和 Liang[23 ] 考虑金融市场中具有固定和比例交易成本, 研究了保险公司的最优融资和股利控制问题. Hobson 等[24 ] 求解了金融市场中具有比例交易成本和单一风险资产的默顿问题. Mei 和 Nogales[25 ] 假设金融市场中存在多个风险资产和比例交易成本, 在收益可预测的情况下研究了多阶段的投资组合选择问题. Melnyk 等[26 ] 探讨了在等弹性递归效用下, 具有小交易成本的终身消费和投资组合选择问题. Gârleanu 和 Pedersen[27 ] 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
Portfolio selection with proportional transaction costs and predictability
1
2018
... 以上所有的研究都假设市场是无摩擦的, 忽略了在金融市场中投资的交易成本. 然而, 在实际的投资交易中, 交易成本是不可避免的, 投资于风险资产时通常需要支付相应的交易费用, 这会一定程度上降低交易策略的收益. 因此, 不应忽视交易成本对投资绩效的影响. Yoshimoto[22 ] 研究了受交易成本影响的投资组合优化问题, 实证分析表明, 忽略交易成本会导致投资组合效率低下. He 和 Liang[23 ] 考虑金融市场中具有固定和比例交易成本, 研究了保险公司的最优融资和股利控制问题. Hobson 等[24 ] 求解了金融市场中具有比例交易成本和单一风险资产的默顿问题. Mei 和 Nogales[25 ] 假设金融市场中存在多个风险资产和比例交易成本, 在收益可预测的情况下研究了多阶段的投资组合选择问题. Melnyk 等[26 ] 探讨了在等弹性递归效用下, 具有小交易成本的终身消费和投资组合选择问题. Gârleanu 和 Pedersen[27 ] 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
Lifetime investment and consumption with recursive preferences and small transaction costs
1
2020
... 以上所有的研究都假设市场是无摩擦的, 忽略了在金融市场中投资的交易成本. 然而, 在实际的投资交易中, 交易成本是不可避免的, 投资于风险资产时通常需要支付相应的交易费用, 这会一定程度上降低交易策略的收益. 因此, 不应忽视交易成本对投资绩效的影响. Yoshimoto[22 ] 研究了受交易成本影响的投资组合优化问题, 实证分析表明, 忽略交易成本会导致投资组合效率低下. He 和 Liang[23 ] 考虑金融市场中具有固定和比例交易成本, 研究了保险公司的最优融资和股利控制问题. Hobson 等[24 ] 求解了金融市场中具有比例交易成本和单一风险资产的默顿问题. Mei 和 Nogales[25 ] 假设金融市场中存在多个风险资产和比例交易成本, 在收益可预测的情况下研究了多阶段的投资组合选择问题. Melnyk 等[26 ] 探讨了在等弹性递归效用下, 具有小交易成本的终身消费和投资组合选择问题. Gârleanu 和 Pedersen[27 ] 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
Dynamic trading with predictable returns and transaction costs
3
2013
... 以上所有的研究都假设市场是无摩擦的, 忽略了在金融市场中投资的交易成本. 然而, 在实际的投资交易中, 交易成本是不可避免的, 投资于风险资产时通常需要支付相应的交易费用, 这会一定程度上降低交易策略的收益. 因此, 不应忽视交易成本对投资绩效的影响. Yoshimoto[22 ] 研究了受交易成本影响的投资组合优化问题, 实证分析表明, 忽略交易成本会导致投资组合效率低下. He 和 Liang[23 ] 考虑金融市场中具有固定和比例交易成本, 研究了保险公司的最优融资和股利控制问题. Hobson 等[24 ] 求解了金融市场中具有比例交易成本和单一风险资产的默顿问题. Mei 和 Nogales[25 ] 假设金融市场中存在多个风险资产和比例交易成本, 在收益可预测的情况下研究了多阶段的投资组合选择问题. Melnyk 等[26 ] 探讨了在等弹性递归效用下, 具有小交易成本的终身消费和投资组合选择问题. Gârleanu 和 Pedersen[27 ] 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
... 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
... 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
Dynamic portfolio choice with frictions
5
2016
... 以上所有的研究都假设市场是无摩擦的, 忽略了在金融市场中投资的交易成本. 然而, 在实际的投资交易中, 交易成本是不可避免的, 投资于风险资产时通常需要支付相应的交易费用, 这会一定程度上降低交易策略的收益. 因此, 不应忽视交易成本对投资绩效的影响. Yoshimoto[22 ] 研究了受交易成本影响的投资组合优化问题, 实证分析表明, 忽略交易成本会导致投资组合效率低下. He 和 Liang[23 ] 考虑金融市场中具有固定和比例交易成本, 研究了保险公司的最优融资和股利控制问题. Hobson 等[24 ] 求解了金融市场中具有比例交易成本和单一风险资产的默顿问题. Mei 和 Nogales[25 ] 假设金融市场中存在多个风险资产和比例交易成本, 在收益可预测的情况下研究了多阶段的投资组合选择问题. Melnyk 等[26 ] 探讨了在等弹性递归效用下, 具有小交易成本的终身消费和投资组合选择问题. Gârleanu 和 Pedersen[27 ] 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
... ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
... 参考文献 [29 ], 考虑二次型交易成本, 该文研究动态均值-方差准则下保险公司的最优风险控制与投资问题. 假设金融市场由无风险资产和多种风险资产组成, 并且运用跳扩散过程来描述保险公司单位风险的动态模型. 与现有的均值-方差准则下的最优风险控制和投资问题的文献相比, 包括文献 [18 ⇓ ⇓ -21 ] 等, 本文将二次型交易成本纳入模型, 并且假设保险风险与金融风险存在相关性. 虽然 Garleanu 和 Pedersen[28 ] , Ma 等[29 ] 和 Bensoussan 等[30 ] 均考虑了二次型交易成本, 但是这些工作并没有考虑到保险风险控制以及保险风险与金融风险的相关性. 在博弈论框架下, 通过求解扩展的 HJB 方程组, 我们得到了依赖于矩阵 Riccati 方程组的解的均衡策略和相应的值函数. 此外, 还进一步研究了一些特殊情况, 并给出了均衡策略和值函数的更具体的表达式. 通过数值分析发现, 随着交易成本水平或相关系数的增加, 投资的增长率会减小. 并且交易成本水平的增加会导致更差的有效前沿. ...
... 在现实中, 投资策略的选取会受到市场摩擦的影响, 如交易成本, 市场波动, 资本利得税等. 其中交易成本最为常见, 并受到研究人员和投资者的广泛关注. 交易成本会在一定程度上影响投资者的投资组合选择, 且忽视交易成本可能会导致较大损失和投资效率的降低. 设 ${\pi _i}(t)$ $i$ $i = 1,2,\cdots,n$ . 记 $\boldsymbol{\pi} (t) = {\left[ {{\pi _1}(t),{\pi _2}(t), \cdots, {\pi _n}(t)} \right]^ \top }$ . Gârleanu 和 Pedersen[28 ] 指出资产头寸的非光滑变动可能会导致无限的交易成本, 所以本文只考虑光滑或者绝对连续的投资组合 $\boldsymbol{\pi} (t)$ . 即存在 $\boldsymbol{\varphi} (t) = {\left[ {{\varphi _1}(t),{\varphi _2}(t), \cdots, {\varphi _n}(t)} \right]^ \top }$
... 以下将 $\boldsymbol{\varphi} (t)$ [28 ] , 假设交易 $\boldsymbol{\varphi} (t){\rm d}t$ $\boldsymbol{\varphi} (t){\rm d}t$
Dynamic portfolio choice with return predictability and transaction costs
4
2019
... 以上所有的研究都假设市场是无摩擦的, 忽略了在金融市场中投资的交易成本. 然而, 在实际的投资交易中, 交易成本是不可避免的, 投资于风险资产时通常需要支付相应的交易费用, 这会一定程度上降低交易策略的收益. 因此, 不应忽视交易成本对投资绩效的影响. Yoshimoto[22 ] 研究了受交易成本影响的投资组合优化问题, 实证分析表明, 忽略交易成本会导致投资组合效率低下. He 和 Liang[23 ] 考虑金融市场中具有固定和比例交易成本, 研究了保险公司的最优融资和股利控制问题. Hobson 等[24 ] 求解了金融市场中具有比例交易成本和单一风险资产的默顿问题. Mei 和 Nogales[25 ] 假设金融市场中存在多个风险资产和比例交易成本, 在收益可预测的情况下研究了多阶段的投资组合选择问题. Melnyk 等[26 ] 探讨了在等弹性递归效用下, 具有小交易成本的终身消费和投资组合选择问题. Gârleanu 和 Pedersen[27 ] 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
... 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
... 参考文献 [29 ], 考虑二次型交易成本, 该文研究动态均值-方差准则下保险公司的最优风险控制与投资问题. 假设金融市场由无风险资产和多种风险资产组成, 并且运用跳扩散过程来描述保险公司单位风险的动态模型. 与现有的均值-方差准则下的最优风险控制和投资问题的文献相比, 包括文献 [18 ⇓ ⇓ -21 ] 等, 本文将二次型交易成本纳入模型, 并且假设保险风险与金融风险存在相关性. 虽然 Garleanu 和 Pedersen[28 ] , Ma 等[29 ] 和 Bensoussan 等[30 ] 均考虑了二次型交易成本, 但是这些工作并没有考虑到保险风险控制以及保险风险与金融风险的相关性. 在博弈论框架下, 通过求解扩展的 HJB 方程组, 我们得到了依赖于矩阵 Riccati 方程组的解的均衡策略和相应的值函数. 此外, 还进一步研究了一些特殊情况, 并给出了均衡策略和值函数的更具体的表达式. 通过数值分析发现, 随着交易成本水平或相关系数的增加, 投资的增长率会减小. 并且交易成本水平的增加会导致更差的有效前沿. ...
... [29 ] 和 Bensoussan 等[30 ] 均考虑了二次型交易成本, 但是这些工作并没有考虑到保险风险控制以及保险风险与金融风险的相关性. 在博弈论框架下, 通过求解扩展的 HJB 方程组, 我们得到了依赖于矩阵 Riccati 方程组的解的均衡策略和相应的值函数. 此外, 还进一步研究了一些特殊情况, 并给出了均衡策略和值函数的更具体的表达式. 通过数值分析发现, 随着交易成本水平或相关系数的增加, 投资的增长率会减小. 并且交易成本水平的增加会导致更差的有效前沿. ...
Dynamic mean-variance problem with frictions
2
2022
... 以上所有的研究都假设市场是无摩擦的, 忽略了在金融市场中投资的交易成本. 然而, 在实际的投资交易中, 交易成本是不可避免的, 投资于风险资产时通常需要支付相应的交易费用, 这会一定程度上降低交易策略的收益. 因此, 不应忽视交易成本对投资绩效的影响. Yoshimoto[22 ] 研究了受交易成本影响的投资组合优化问题, 实证分析表明, 忽略交易成本会导致投资组合效率低下. He 和 Liang[23 ] 考虑金融市场中具有固定和比例交易成本, 研究了保险公司的最优融资和股利控制问题. Hobson 等[24 ] 求解了金融市场中具有比例交易成本和单一风险资产的默顿问题. Mei 和 Nogales[25 ] 假设金融市场中存在多个风险资产和比例交易成本, 在收益可预测的情况下研究了多阶段的投资组合选择问题. Melnyk 等[26 ] 探讨了在等弹性递归效用下, 具有小交易成本的终身消费和投资组合选择问题. Gârleanu 和 Pedersen[27 ] 假设每笔交易都会对风险资产产生一个线性的瞬时价格影响, 由此导出交易成本是二次型的, 并在离散时间框架下研究了具有收益可预测的最优投资组合问题. 在文献 [27 ] 的基础上, Garleanu 和 Pedersen[28 ] 在连续时间框架下考虑了具有二次型交易成本, 且收益可预测时的投资组合选择问题, 得到了最优投资策略的显式表达式, 并证明了文献 [27 ] 中离散时间情况下解的极限与文献 [28 ] 中的解是一致的. Ma 等[29 ] 研究了存在二次型交易成本和收益可预测的最优交易策略, 其目标是使终端财富的指数效用最大化. 结果表明, 最优交易策略将逐渐收敛于由未来默顿投资组合的期望的加权和所构成的目标投资组合. 在文献 [29 ] 的基础上, Bensoussan 等[30 ] 进一步研究了在均值-方差准则下具有收益可预测和二次型交易成本的投资组合问题, 并表明交易策略应逐步向目标投资组合靠近. ...
... 参考文献 [29 ], 考虑二次型交易成本, 该文研究动态均值-方差准则下保险公司的最优风险控制与投资问题. 假设金融市场由无风险资产和多种风险资产组成, 并且运用跳扩散过程来描述保险公司单位风险的动态模型. 与现有的均值-方差准则下的最优风险控制和投资问题的文献相比, 包括文献 [18 ⇓ ⇓ -21 ] 等, 本文将二次型交易成本纳入模型, 并且假设保险风险与金融风险存在相关性. 虽然 Garleanu 和 Pedersen[28 ] , Ma 等[29 ] 和 Bensoussan 等[30 ] 均考虑了二次型交易成本, 但是这些工作并没有考虑到保险风险控制以及保险风险与金融风险的相关性. 在博弈论框架下, 通过求解扩展的 HJB 方程组, 我们得到了依赖于矩阵 Riccati 方程组的解的均衡策略和相应的值函数. 此外, 还进一步研究了一些特殊情况, 并给出了均衡策略和值函数的更具体的表达式. 通过数值分析发现, 随着交易成本水平或相关系数的增加, 投资的增长率会减小. 并且交易成本水平的增加会导致更差的有效前沿. ...