空间分数阶 KGS 方程组的辛差分格式

空间分数阶 KGS 方程组的辛差分格式

王俊杰^,

普洱学院数学与统计学院云南普洱 665000

Symplectic Difference Scheme for the Space Fractional KGS Equations

Wang Junjie^,

School of Mathematics and Statistics, Pu'er University, Yunnan Pu'er 665000

收稿日期: 2022-11-7 修回日期: 2024-03-26

基金资助:

国家自然科学基金(12161070)

Received: 2022-11-7 Revised: 2024-03-26

Fund supported:

National Natural Science Foundation of China(12161070)

作者简介 About authors

王俊杰,E-mail:ynpewjj@126.com

摘要

该文研究分数阶 KGS 方程组的辛差分格式. 首先, 作者给出了无穷维分数阶 Hamilton 系统, 并将 KGS 方程组转化为 Hamilton 系统. 然后, 基于分数阶中心差分格式对分数阶 KGS 方程组进行空间离散, 得到的半离散系统是一个有限维 Hamilton 系统. 接着, 利用辛中点格式对时间进行离散得到全离散格式, 并且对该格式进行了守恒性分析. 最后, 通过数值实验验证了该数值格式的有效性.

关键词： 分数阶 KGS 方程组; 守恒格式; 辛格式; 收敛性

Abstract

In the paper, the symplectic-preserving schemes are presented for fractional Klein-Gordon-Schrödinger equations. First, we give the infinite-dimensional Hamilton with fractional Laplacian operator and conservation laws, and change the above quantum mechanical equations into Hamilton system. We apply the central finite difference schemes to discrete Klein-Gordon-Schrödinger in space, and yield a large Hamilton ordinary differential system. Second, we use the midpoint rule in time to Hamiltonian ordinary differential system, and obtain a symplectic approximation of the these equations. Moreover, we analyze the conservation of the numerical scheme. Finally, we give numerical experiments to show the verify the efficiency of the conservative finite difference scheme.

Keywords： Fractional Klein-Gordon-Schrödinger equations; Conservative scheme; Symplectic scheme; Convergence

PDF (1742KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王俊杰. 空间分数阶 KGS 方程组的辛差分格式[J]. 数学物理学报, 2024, 44(5): 1318-1333

Wang Junjie. Symplectic Difference Scheme for the Space Fractional KGS Equations[J]. Acta Mathematica Scientia, 2024, 44(5): 1318-1333

1 引言

Hamilton 系统是一类非常重要的动力系统, 在数学、力学和工程科学, 特别是在非线性科学领域等发挥着重要作用. 冯康院士曾指出, 一切真实的无耗散的物理过程都可以表示为 Hamilton 形式, 在数学上可以用常微分方程或偏微分方程表示, 因此研究 Hamilton 系统^{[1⇓⇓⇓⇓⇓-7]}有重要的意义. 经典的无限维 Hamilton 系统可以表示为

$\begin{eqnarray*} \frac{\partial}{\partial t}z=\mathcal{D}\frac{\delta \mathcal{H}(z)}{\delta z}, \end{eqnarray*}$

其中 $\mathcal{D}$ 为 Hamilton 算符, $\mathcal{H}(z)=\int_{\Omega}H(x,z_x,z_{xx},\cdots){\rm d}x$ 为 Hamilton 函数.

由变分导数

$\begin{eqnarray*} \frac{\delta \mathcal{H} }{\delta z}=\frac{\partial H}{\partial z}-\partial_x(\frac{\partial H}{\partial z_x})+\partial_x^2(\frac{\partial^2 H}{\partial z_{xx}^2})-\cdots, \end{eqnarray*}$

Hamilton 系统有许多不同于一般动力系统的重要特征, 最重要的是辛和能量守恒

(1.2)$\begin{align*} &\frac{\rm d}{{\rm d}t}w=\frac{\rm d}{{\rm d}t}\int_\Omega {\rm d}z\wedge \mathcal{D}{\rm d}z{\rm d}x=0,\end{align*}$

(1.3)$\begin{align*} &\frac{\rm d\mathcal{H}}{{\rm d}t}=0. \end{align*}$

众所周知, 守恒律在守恒系统中起着重要的作用, 在过去的几十年中, 保结构算法一直受到人们的广泛关注^{[8⇓⇓⇓⇓⇓⇓-15]}. 在“数值算法应尽可能多的保持原问题的本质特征”的指导下, 1984 年, 我国的冯康院士首次提出了保持辛几何结构的辛算法, 后来, 汪道柳结合谱方法提出了偏微分方程的辛算法, McLachlan 提出了偏微分方程的辛分裂算法. 大量的数值结果显示, 辛算法在解决偏微分方程方面具有明显的优势. 然而, 在这些工作中只考虑了整数阶方程, 据我们所知, 对分数阶方程^{[16⇓⇓⇓⇓⇓⇓⇓⇓-25]} 的辛算法的研究还很少.

最近十几年, 分数阶微分方程的数值方法取得丰硕的研究成果. 首先, 基于 Grunwald-Letnikov 定义建立了分数阶 Riemann-Liouville 导数和分数阶 Riesz 导数的差分格式^[18], 并用该格式求解时间分数阶和空间分数阶微分方程. 其次, 对分数阶 Caputo 导数和时间分数阶微分方程进行了广泛的研究^{[18,26⇓⇓⇓⇓⇓-32]}. 最近, 分数阶 Laplacian 算子在反常扩散、多孔介质力学、非牛顿流体力学、粘弹性力学、软物质物理研究等领域受到越来越广泛的关注, 也取得一定研究成果,如得到了分数阶中心差分格式、分数阶 WSGD 格式、分数阶紧差分格式等^[18], 并利用这些格式对分数阶 Laplacian 微分方程进行了数值模拟和理论分析. 本文考虑如下含有分数阶 Laplacian 算子无限维 Hamilton 系统^[33,34]

(1.4)$\begin{eqnarray*} \frac{\partial}{\partial t}z=\mathcal{D}\frac{\delta \mathcal{H}(z, z_x, z_{xx},\cdots, (-\triangle)^{\frac{\alpha}{2}}z)}{\delta z}, \end{eqnarray*}$

其中 $\mathcal{H}(z, z_x, z_{xx}, \cdots, (-\triangle)^{\frac{\alpha}{2}}z)=\int_\Omega H(z,z_x,x_{xx},\cdots, (-\triangle)^{\frac{\alpha}{2}}z){\rm d}x.$ 分数阶 Laplacian 算子可以表示为

$\begin{equation*} -(-\Delta)^{\frac{\alpha}{2}}u(x,t)=-\mathcal{F}^{-1}(|\xi|^\alpha \mathcal{F}(u(\xi,t))), \end{equation*}$

其中 $\mathcal{F}$ 为 Fourier 变换. 对于上述分数阶无限维 Hamilton系统 (1.4) 已经开展一些研究, 并取得不错的效果. 文献 [33] 给出了薛定谔方程的辛差分格式, 文献 [34] 给出分数阶 Klein-Gordon-Schrödinger (KGS) 方程组的 Fourier 辛格式, 文献 [35] 给出了薛定谔方程的多辛格式. 然而, 大部分的保辛结构数值格式是非线性格式, 需要进行迭代求解, 精度往往比较低. 分数阶无限维 Hamilton 系统的高阶数值方法研究还比较少.

本文主要应用分数阶无限维 Hamilton 系统来研究分数阶 KGS 方程组, 并构造该方程组的高阶数值格式. 首先, 通过一些引理将分数阶 KGS 方程组转化为分数阶无限维 Hamilton 系统 (1.4), 然后我们给出分数阶 Laplacian 算子高阶数值格式, 并利用该格式对分数阶 KGS 方程组进行空间离散, 得到一个有限维 Hamilton 系统, 并验证半离散差分格式满足离散辛守恒律和能量守恒律, 接着给出半离散格式的辛算法, 并证明该格式的收敛性. 最后, 给出了数值实验, 验证了理论结果的正确性和有效性.

2 分数阶 KGS 方程组半离散格式

在这一节, 我们首先将分数阶 KGS 系统转化为分数阶无限维 Hamilton 系统, 并给出分数阶 Laplacian 算子数值格式, 利用该格式对分数阶 KGS 方程组进行空间离散, 并对该格式进行理论分析.

引理 2.1^[36] 对于 $f, g\in H_p^{2\alpha}(\Omega)$, 有

$\int_{\Omega}(-\Delta)^\alpha f\cdot g{\rm d}x=\int_\Omega(-\Delta)^{\alpha_1} f\cdot(-\Delta)^{\alpha_2}g{\rm d}x,$

其中 $\alpha_1, \alpha_2\geq0$, $\alpha_1+\alpha_2=\alpha$, $H_p^{2\alpha}(\Omega)$ 表示索伯列夫周期函数空间.

引理 2.2^[34] 对于 $\mathcal{H}(z, z_x, z_{xx}\cdots(-\triangle)^{\frac{\alpha}{2}}z)=\int_\Omega H(z,z_x,x_{xx},\cdots, (-\triangle)^{\frac{\alpha}{2}}z){\rm d}x$, 有

$\begin{eqnarray*} \frac{\delta \mathcal{H} }{\delta z}=\frac{\partial H}{\partial z}-\partial_x(\frac{\partial H}{\partial z_x})+\partial_x^2(\frac{\partial H}{\partial z_{xx}})-\cdots+(-\triangle)^{\frac{\alpha}{4}}\frac{\partial H}{\partial((-\triangle)^{\frac{\alpha}{4}}z)}. \end{eqnarray*}$

在周期边界条件下, 考虑分数阶 KGS 方程组

(2.1)$\begin{eqnarray*} &&{\rm i} u_t-\frac{1}{2}(-\Delta)^{\frac{\alpha}{2}}u=u\phi, \end{eqnarray*}$

(2.2)$\begin{eqnarray*} &&\phi_{tt}+(-\Delta)^{\frac{\beta}{2}}\phi+m\phi=|u|^2, \end{eqnarray*}$

(2.3)$\begin{eqnarray*} &&u(x,0)=u_0(x),\phi(x,0)=\phi_0(x),\phi_t(x,0)=\phi_1(x), \end{eqnarray*}$

(2.4)$\begin{eqnarray*} &&u(x-\frac{L}{2},t)=u(x+\frac{L}{2},t), \phi(x-\frac{L}{2},t)=\phi(x+\frac{L}{2},t). \end{eqnarray*}$

下面我们主要考虑 $m=1$ 的情况.令 $u=p+qi, \phi_t=\psi$, 系统 (2.1)-(2.2) 可以表示为以下形式

(2.5)$\begin{eqnarray*} &&q_t=\frac{1}{2}(-\Delta)^{\frac{\alpha}{2}}p-p\phi, \end{eqnarray*}$

(2.6)$\begin{eqnarray*} &&p_t=-\frac{1}{2}(-\Delta)^{\frac{\alpha}{2}}q+q\phi, \end{eqnarray*}$

(2.7)$\begin{eqnarray*} &&\phi_t=\psi, \end{eqnarray*}$

(2.8)$\begin{eqnarray*} &&\psi_{t}=-(-\Delta)^{\frac{\beta}{2}}\phi-\phi+p^2+q^2. \end{eqnarray*}$

令

$\begin{align*} H(p,q,\phi,\psi)=&\frac{1}{2}((-\Delta)^{\alpha_1}p\cdot(-\Delta)^{\alpha_2}p+(-\Delta)^{\alpha_1}q\cdot(-\Delta)^{\alpha_2}q)\\ &+\frac{1}{2}(p^2+q^2)\phi-\frac{1}{2}\psi^2-\frac{1}{2}\phi^2 +(-\Delta)^{\beta_1}\phi\cdot(-\Delta)^{\beta_2}\phi, \end{align*}$

其中 $ \alpha_1+\alpha_2=\frac{\alpha}{2}$, $ \beta_1+\beta_2=\frac{\beta}{2}$, 利用引理 2.1-2.2, 系统 (2.5)-(2.8) 可以表示为分数阶无限维 Hamilton 系统 (1.4).

2.1 分数阶 Laplacian 算子高阶数值格式

记

$\begin{align*} \Omega_h=&\{x_j|1\leq j\leq J-1\}, \Omega_\tau=\{t_n|1\leq n\leq N-1\},\\ \bar{\Omega}_h=&\{x_j|0\leq j\leq J\}, \bar{\Omega}_\tau=\{t_n|0\leq n\leq N\}. \end{align*}$

令 $\{w_j^n\}$ 为 $\Omega_h \times \Omega_\tau$ 上的网格函数, 定义差分运算符

$\begin{eqnarray*} &&w_j^{n+\frac{1}{2}}=\frac{w_{j}^{n+1}+w_j^n}{2},(w_j^n)_{\hat{t}}=\frac{w_j^{n+1}-w_j^{n-1}}{2\tau},\\ &&(w_j^n)_t=\frac{w_j^{n+1}-w_j^n}{\tau},(w_j^n)_{\overline{t}}=\frac{w_j^{n}-w_j^{n-1}}{\tau}. \end{eqnarray*}$

对于网格 $w=\{w_j\},v=\{v_j\}$, 定义如下离散内积, $l_2$ 范数以及 $l_p$ 范数为

$\begin{eqnarray*} && \langle w,v\rangle=h\sum w_j\overline{v}_j,\|w\|^2=\langle w,w\rangle,\\ &&\|w\|_{l_h^p}^p=h\sum |w_j|^p,1\leq p<+\infty. \end{eqnarray*}$

当 $p =\infty$, 有

$\begin{eqnarray*} &&\|w\|_{l_h^{\infty}}=\sup_{j\in Z}|w_j|. \end{eqnarray*}$

引理 2.3^[16] 假设 $w\in L_1(R)$,且

$w\in \mathcal{L}^{2+\alpha}(R):=\{w|\int_{-\infty}^{+\infty}(1+|\xi|)^{2+\alpha}|\mathcal{F}(w(\xi))|{\rm d}\xi<\infty\}. $

对于固定 $h$, 有

(2.9)$\begin{equation} -\Delta_{h}^\alpha w(x)=-(-\Delta)^{\frac{\alpha}{2}}w(x)+O(h^2), (1<\alpha\leq2), \end{equation}$

其中

(2.10)$\begin{eqnarray*} -\Delta_{h}^\alpha w(x)=\displaystyle h^{-\alpha}\sum\limits_{k=-\infty}^\infty g_k^{(\alpha)}w(x-kh), g_k^{(\alpha)}=\frac{(-1)^k\Gamma(\alpha+1)}{\Gamma(\frac{\alpha}{2}-k+1)(\Gamma(\frac{\alpha}{2}+k+1)}. \end{eqnarray*}$

引理 2.4^[33] 假设 $w\in L_1(R)$, 且

$w\in \mathcal{L}^{4+\alpha}(R):=\{w|\int_{-\infty}^{+\infty}(1+|\xi|)^{2+\alpha}|\mathcal{F}(w(\xi))|{\rm d}\xi<\infty\}, $

对于固定的 $h$, 有

(2.11)$\begin{equation} \delta_h^\alpha w(x)=-(-\Delta)^{\frac{\alpha}{2}}w(x)+O(h^4),(1<\alpha\leq2). \end{equation}$

其中

$\begin{eqnarray*} &&\displaystyle \delta_h^\alpha w(x)=\frac{-4h^{-\alpha}}{3}\sum\limits_{k=-\infty}^\infty g_k^{(\alpha)}w(x-kh)+\frac{(2h)^{-\alpha}}{3}\sum\limits_{k=-\infty}^\infty g_k^{(\alpha)}w(x-2kh), \\ && |2\sin\frac{x}{2}|^\alpha=\sum\limits_{k=-\infty}^\infty g_k^{(\alpha)}{\rm e}^{{\rm i}kx}. \end{eqnarray*}$

本文主要应用分数阶 Laplacian 算子的 4 阶格式求解分数阶 KGS 方程组. 事实上在文献 [25] 中, 我们已经将该分数阶 Laplacian 算子的数值格式推广到 6 阶, 8 阶格式, 用类似的方法我们可以得到分数阶 KGS 方程组的 6 阶和 8 阶数值格式.

从引理 2.3-2.4 得到

(2.12)$\begin{equation}-(-\Delta)^{\frac{\alpha}{2}} w(x)=-\frac{1}{h^\alpha}(\sum\limits_{k=-\infty}^{+\infty}g_{k,q}^{(\alpha)})w(x-kh)+O(h^{\sigma(q)}), \end{equation}$

其中, 当 $q=1$ 时, $\sigma(q)=2$；当 $q=2$时, $\sigma(q)=4, $

$ \displaystyle g_{k,q}^{(\alpha)}=\left\{ \begin{array}{lcl} g_{k}^{(\alpha)},q=1,\\ \widehat{g}_{k}^{(\alpha)},q=2, \end{array} \right.$

且

$ \displaystyle \widehat{g}_k^{(\alpha)}=\left\{ \begin{array}{lcl} \frac{4}{3}g_k^{(\alpha)}-\frac{1}{3\cdot2^\alpha}g_{\frac{k}{2}}^{(\alpha)},\quad & k\in\mbox{偶数},\\[3mm] \frac{4}{3}g_k^{(\alpha)},& k\in\mbox{奇数}. \end{array} \right.$

本文主要考虑周期边界条件的数值格式, 注意到引理 2.3-2.4, 在周期边界条件下得到如下数值格式

(2.13)$\begin{equation}-(-\Delta)^{\frac{\alpha}{2}} u(x,t)=-\frac{1}{h^\alpha}\sum\limits_{k=0}^{J-1}(\sum\limits_{l=-\infty}^{+\infty}g_{k+lJ,q}^{(\alpha)})u(x-kh,t)+O(h^{\sigma(q)}). \end{equation}$

取离散点 $(x_j, t_n)$, 记精确值和数值解分别为 $u^n_j=u(x_j, t_n), \phi_j^n=\phi(x_j, t_n)$; $U^n_j=u(x_j, t_n),$$\Phi_j^n=\phi(x_j, t_n)$. 通过数值格式 (2.13) 得到如下格式

$\begin{align*} -(-\Delta)^{\frac{\alpha}{2}} u_j^n&=-\frac{1}{h^\alpha}\sum\limits_{k=0}^{J-1}(\sum\limits_{l=-\infty}^{+\infty}g_{k+lJ,q}^{(\alpha)})u_{j-k}^n+O(h^{\sigma(q)})\\ &=-\frac{1}{h^\alpha}\sum\limits_{k=0}^{J-1}(\sum\limits_{l=-\infty}^{+\infty}g_{j-k+lJ,q}^{(\alpha)})u_{k}^n+O(h^{\sigma(q)}). \end{align*}$

通过上面方程, 我们可以定义分数阶 Laplacian 算子的离散格式为

(2.14)$\begin{equation} \displaystyle -(-\Delta)^{\frac{\alpha}{2}} u_j^n\approx L^{(\alpha)}_{h,q}U_j^n=\left\{ \begin{array}{lcl} \displaystyle h^{-\alpha}\sum\limits_{k=0}^{J-1}(\sum\limits_{l=-\infty}^\infty g_{k+lJ}^{(\alpha)}U_{k}^n), q=1,\\ \displaystyle h^{-\alpha}\sum\limits_{k=0}^{J-1}(\sum\limits_{l=-\infty}^\infty \widehat{g}_{k+lJ}^{(\alpha)}U_{k}^n), q=2. \end{array} \right.\end{equation}$

定义

$ G^{(q)}=\left[\begin{array}{cccc} \displaystyle\sum\limits_{l=-\infty}^{\infty}g_{0+lJ,q}^{(\alpha)}&\displaystyle\sum\limits_{l=-\infty}^{\infty}g_{-1+lJ,q}^{(\alpha)}&\cdots &\displaystyle\sum\limits_{l=-\infty}^{\infty}g_{-J+1+lJ,q}^{(\alpha)}\\ \displaystyle\sum\limits_{l=-\infty}^{\infty}g_{1+lJ,q}^{(\alpha)}&\displaystyle\sum\limits_{l=-\infty}^{\infty}g_{0+lJ,q}^{(\alpha)}&\cdots &\displaystyle\sum\limits_{l=-\infty}^{\infty}g_{-J+2+lJ,q}^{(\alpha)}\\ \vdots&\vdots&\ddots&\vdots\\ \displaystyle\sum\limits_{l=-\infty}^{\infty}g_{J-1+lJ,q}^{(\alpha)}&\displaystyle\sum\limits_{l=-\infty}^{\infty}g_{J-2 +lJ,q}^{(\alpha)}&\cdots &\displaystyle\sum\limits_{l=-\infty}^{\infty}g_{0+lJ,q}^{(\alpha)} \end{array}\right]. $

注意到无穷级数 $ \sum\limits_{l=-\infty}^{\infty}g_{k+lJ,q}^{(\alpha)}, (-J+1\leq k \leq J-1)$ 是收敛的, 可以找到一组数 $\widetilde{g}_{k,q}^{(\alpha)}$ 满足 $ \sum\limits_{l=-\infty}^{\infty}g_{k+lJ,q}^{(\alpha)}=\widetilde{g}_{k,q}^{(\alpha)}$, 并且 $G^{(q)}$ 可以表示为如下形式

$ G^{(q)}=\left[\begin{array}{cccc} \displaystyle \widetilde{g}_{0,q}^{(\alpha)} &\widetilde{g}_{-1,q}^{(\alpha)}&\cdots &\displaystyle\widetilde{g}_{-J+1,q}^{(\alpha)}\\ \displaystyle \widetilde{g}_{1,q}^{(\alpha)} &\widetilde{g}_{0,q}^{(\alpha)}&\cdots &\displaystyle\widetilde{g}_{-J+2,q}^{(\alpha)}\\ \vdots&\vdots&\ddots&\vdots\\ \displaystyle \widetilde{g}_{J-1,q}^{(\alpha)} &\widetilde{g}_{J-2,q}^{(\alpha)}&\cdots &\displaystyle\widetilde{g}_{0,q}^{(\alpha)} \end{array}\right]. $

通过文献 [21,25] 类似的方法, 我们可以得到如下引理.

引理 2.5 对于系数 $\widetilde{ g}_{k,q}^{(\alpha)}$ 和参数 $1<\alpha \leq 2$, 有如下性质

$\widetilde{g}_{0,q}^{(\alpha)}>0, \widetilde{g}_{k,q}^{(\alpha)}=\widetilde{g}_{-k,q}^{(\alpha)}<0, \widetilde{g}_{-J+k,q}^{(\alpha)}=\widetilde{g}_{k,q}^{(\alpha)}.$

引理 2.6 记 $\lambda_i$ 是矩阵 $G^{(q)}$ 的特征值, 则 $\lambda_i$ 满足

$0<\lambda_i<2\widetilde{g}_{0,q}^{(\alpha)},$

并且矩阵 $G^{(q)}$ 是一个实值对称正定矩阵.

引理 2.7 对于任意两个网格函数 $U,V\in Z_h^0$, 存在一个线性算子 $\Lambda^\alpha$ 满足

$\langle L^{(\alpha)}_{h,q} U,V\rangle=\langle\Lambda^\alpha U, \Lambda^\alpha V\rangle.$

定义

(2.15)$\begin{equation} |U|_{\alpha/2}=(-h\sum\limits_{j=0}^{J-1}L_{h,q}^{(\alpha)}U_j\overline{U}_j)^\frac{1}{2}, U=(U_0,U_1,\cdots,U_{J-1})^T, \end{equation}$

易得如下结论

(2.16)$\begin{equation} |U|_{\alpha/2}=(h^{1-\alpha}\overline{U}G^{(q)}U^T)^{\frac{1}{2}}. \end{equation}$

引理 2.8 对于网格函数 $U^n\in Z_h^0$, 有

(2.17)$\begin{eqnarray*} \mbox{Im}\langle L^{(\alpha)}_{h,q} U^{n+\frac{1}{2}},U^{n+\frac{1}{2}}\rangle&=&0, \end{eqnarray*}$

(2.18)$\begin{eqnarray*} \mbox{Re}\langle L^{(\alpha)}_{h,q} U^{n+\frac{1}{2}},U^{n}_t\rangle&=&\frac{1}{2\tau}(\|\Lambda^\alpha U^{n+1}\|^2 -\|\Lambda^\alpha uU^n\|^2), \end{eqnarray*}$

其中 $\mbox{Im}(s), \mbox{Re}(s)$ 分别为复数 $s$ 的虚部和实部.

引理 2.9^[25] (Diserete Sobolev 不等式) 对于 $\frac{1}{2}\leq \delta\leq1$, 存在一个不依赖于 $h>0$ 的常数 $C=C(\delta)>0$ 满足

$\|u\|_{l_h^{\infty}}\leq C_{\sigma}\|u\|_{H_h^{\delta}}.$

引理 2.9^[25] (Gagliardo-Nirenberg 不等式) 对于 $ \frac{p-2}{2p}<\delta_0\leq 1,$ 存在一个不依赖于 $h>0$ 的常数 $C_{\delta_0}=C(\delta_0)>0$ 满足

$\|u\|_{l^p_h}\leq C_{\delta_0}\|u\|_{H^\delta}^{\delta_0/\delta}\|u\|^{1-\delta_0/\delta}.$

2.2 半离散格式

通过数值格式 (2.14) 可以得到分数阶 KGS 方程组的半离散格式

(2.19)$\begin{eqnarray*} &&{\rm i}\frac{{\rm d}U_{j}}{{\rm d}t}+\frac{1}{2}L_{h,p}^\alpha U_{j}=U_{j}\Phi_{j}, \end{eqnarray*}$

(2.20)$\begin{eqnarray*} &&\frac{{\rm d}^2\Phi_{j}}{{\rm d}t^2}-L_{h,p}^\beta\Phi_{j}+\Phi_{j}=|U_{j}|^2, \end{eqnarray*}$

(2.21)$\begin{eqnarray*} &&U_j^0=u_0(x_j),\Phi_j^0=\phi_0(x_j),(\Phi_j^0)_t=\phi_1(x_j). \end{eqnarray*}$

令$U(t)=(U_1(t),U_2(t),\cdots, U_{J-1}(t)),\Phi(t)=(\Phi_1(t),\Phi_2(t),\cdots, \Phi_{J-1}(t)),$

方程 (2.19)-(2.20) 可以表示为如下紧凑形式

(2.22)$\begin{eqnarray*} &&{\rm i}\frac{{\rm d}U}{{\rm d}t}+\frac{1}{2}L_{h,p}^\alpha U=U\cdot \Phi, \end{eqnarray*}$

(2.23)$\begin{eqnarray*} &&\frac{{\rm d}^2\Phi}{{\rm d}t^2}-L_{h,p}^\beta \Phi+\Phi=|U|^2. \end{eqnarray*}$

定理 2.1 分数阶 KGS 方程组的数值格式 (2.22)-(2.23) 是守恒的,并且满足如下表达式

$\begin{align*} M(t)=&\|U\|=M(0), \\ E(t)=&\|\Lambda^{\alpha}U\|^2+\|\frac{{\rm d}\Phi}{{\rm d}t} \|^2+\|\Lambda^\beta\Phi\|^2+\|\Phi\|^2-2h\sum\limits_{j=0}^{J-1}|U_j|^2\Phi_j=E(0). \end{align*}$

证计算 $U$ 与方程 (2.22) 的内积, 并取虚部, 得到 $\frac{\rm d}{{\rm d}t}\|U\|^2=0.$ 计算 $\frac{{\rm d}U}{{\rm d}t}$ 与方程 (2.22) 的内积, 并取实部, 得到

(2.24)$\begin{eqnarray*} &&\frac{1}{2}\langle L_{h,p}^\alpha U,\frac{{\rm d}U}{{\rm d}t}\rangle=\langle U\Phi,\frac{{\rm d}U}{{\rm d}t}\rangle, \end{eqnarray*}$

(2.25)$\begin{eqnarray*} &&\frac{1}{2}\frac{\rm d}{{\rm d}t}\|\Lambda^{\alpha}U\|^2=h\sum\limits_{j=0}^{J-1}\frac{{\rm d}|U_j|^2}{{\rm d}t}\Phi_j. \end{eqnarray*}$

计算 $\frac{{\rm d}\Phi}{{\rm d}t}$ 与方程 (2.23) 的内积, 并取实部, 得到

(2.26)$\begin{eqnarray*} &&\langle\frac{{\rm d}^2\Phi}{{\rm d}t^2},\frac{{\rm d}\Phi}{{\rm d}t}\rangle-\langle L_{h,p}^2 \Phi,\frac{{\rm d}\Phi}{{\rm d}t}\rangle+\langle\Phi,\frac{{\rm d}\Phi}{{\rm d}t}\rangle=\langle|U|^2,\frac{{\rm d}\Phi}{{\rm d}t}\rangle, \end{eqnarray*}$

(2.27)$\begin{eqnarray*} &&\frac{1}{2}\frac{{\rm d}}{{\rm d}t}(\|\frac{{\rm d}\Phi}{{\rm d}t} \|^2+\|\Lambda^\beta\Phi\|^2+\|\Phi\|^2)=h\sum\limits_{j=0}^{J-1}|U_j|^2 \frac{{\rm d}\Phi_j}{{\rm d}t}. \end{eqnarray*}$

对方程 (2.25) 和 (2.27) 求和得到

$\frac{1}{2}\frac{{\rm d}}{{\rm d}t}(\|\Lambda^{\alpha}U\|^2+\|\frac{{\rm d}\Phi}{{\rm d}t} \|^2+\|\Lambda^\beta\Phi\|^2+\|\Phi\|^2-2h\sum\limits_{j=0}^{J-1}|U_j|^2\Phi_j)=0.$

即$E(t)=\|\Lambda^{\alpha}U\|^2+\|\frac{{\rm d}\Phi}{{\rm d}t} \|^2+\|\Lambda^\beta\Phi\|^2-\|\Phi\|^2-2h\sum\limits_{j=0}^{J-1}|U_j|^2\Phi_j= E(0).$

证毕.

定理 2.2 假设分数阶 KGS 方程组 (2.1)-(2.2) 有一光滑解, 对于 $p=2$, 分数阶 KGS 方程组 (2.1)-(2.2) 的差分格式 (2.22)-(2.23) 的解依 $l_h^2$ 范数收敛到真解, 其阶是 $O(h^4)$.

证令 $u_j\approx u(x_j),\phi_j\approx\phi(x_j)$, 定义分数阶 KGS 方程组 (2.1)-(2.2) 的差分格式 (2.22)-(2.23) 的局部截断误差为

(2.28)$\begin{eqnarray*} &&R_1={\rm i}\frac{u(x_j)}{{\rm d}t}-\frac{1}{2}L_{h,p}^\alpha u(x_j)-u(x_j)\phi(x_j), \end{eqnarray*}$

(2.29)$\begin{eqnarray*} &&R_2=\frac{{\rm d}^2\phi(x_j)}{{\rm d}t^2}-L_{h,p}^2 \phi(x_j)+\phi(x_j)-|u(x_j)|^2. \end{eqnarray*}$

根据泰勒展开式, 得到 $|R_j|=O(h^{4}), j=1, 2$.

令 $e_j=u(x_j)-U_j,\eta_j=\phi(x_j)-\Phi_j$, 有

(2.30)$\begin{eqnarray*} &&R_1^n={\rm i}\frac{{\rm d}e}{{\rm d}t}-\frac{1}{2} L_{h,p}^\alpha e+u(x_j)\phi(x_j)-U_j\Phi_j, \end{eqnarray*}$

(2.31)$\begin{eqnarray*} &&R_2^n=\frac{{\rm d}^2\eta}{{\rm d}t^2}-L_{h,p}^2 \eta+\eta-|u(x_j)|^2+|U_j|^2. \end{eqnarray*}$

计算 $2 e$ 与方程 (34) 的内积得到

(2.32)$\begin{equation}\langle R_1,2e\rangle=\langle {\rm i}\frac{{\rm d}e}{{\rm d}t}-\frac{1}{2}L_{h,p}^\alpha e+ u(x_j)\phi(x_j)-u_j\phi_j,2e\rangle.\end{equation}$

注意到

$\begin{eqnarray*} |u(x_j)\phi(x_j)-U_j\Phi_j|=|u_j(\phi(x_j)-\Phi_j)-(U_j-u(x_j))\phi(x_j)|, \end{eqnarray*}$

通过定理 2.1 可以得到

$\begin{eqnarray*} |u(x_j)\phi(x_j)-U_j\Phi_j|=C(|e|+|\eta|). \end{eqnarray*}$

取方程 (2.32) 的虚部得到

(2.33)$\begin{equation} \frac{{\rm d}\|e\|^2}{{\rm d}t}\leq \frac{1}{2} \|R_1\|^2+C(\|e\|^2+\|\eta\|^2). \end{equation}$

计算 $\frac{{\rm d}\eta}{{\rm d}t}$ 与方程 (2.31) 的内积可以得到

$\begin{eqnarray*} \langle R_2,2\frac{{\rm d}\eta}{{\rm d}t}\rangle =\langle\frac{{\rm d}^2\eta}{{\rm d}t^2}-L_{h,p}^\beta \eta+\eta-|u(x_j)|^2+|U_j|^2,\frac{{\rm d}\eta}{{\rm d}t}\rangle. \end{eqnarray*}$

注意到 $||u(x_j)|^2-|U_j|^2|\leq C|e|$, 有

(2.34)$\begin{eqnarray*} \frac{{\rm d}}{{\rm d}t}(\|\frac{{\rm d}\eta}{{\rm d}t}\|^2+\|\eta\|^2+\|\Lambda^\beta\eta\|^2)\leq \frac{1}{2} \|R_2\|^2+C(\|\frac{{\rm d}\eta}{{\rm d}t}\|^2+\|e\|^2). \end{eqnarray*}$

对方程 (2.33) 与 (2.34) 求和得到

$\begin{eqnarray*} &&\frac{{\rm d}}{{\rm d}t}(\|\frac{{\rm d}\eta}{{\rm d}t}\|^2+\|e\|^2+\|\eta\|^2+\|\Lambda^\beta\eta\|^2)\\ &\leq& \frac{1}{2}(\|R_1\|^2+ \|R_2\|^2)+C(\|\frac{{\rm d}\eta}{{\rm d}t}\|^2+\|e\|^2+\|\eta\|^2+\|\Lambda^\beta\eta\|^2). \end{eqnarray*}$

通过 Grolwall's 引理得 $\|e\|= O(h^{4}), \|\eta\|=O(h^{4}).$ 证毕.

令$U_j=P_j+{\rm i} Q_j,\frac{{\rm d}\Phi_{j}}{{\rm d}t}=\Psi_j,$

方程 (2.22)-(2.23) 可以表示为如下形式

(2.35)$\begin{eqnarray*} &&-\frac{{\rm d}Q_{j}}{{\rm d}t}=\frac{1}{2} L_{h,p}^\alpha P_{j} +p_{j}\Phi_{j}, \end{eqnarray*}$

(2.36)$\begin{eqnarray*} &&\frac{{\rm d}P_{j}}{{\rm d}t}=\frac{1}{2}L_{h,p}^\alpha Q_{j} +Q_{j}\Phi_{j}, \end{eqnarray*}$

(2.37)$ \begin{eqnarray*} &&\frac{{\rm d}\Phi_{j}}{{\rm d}t}=\Psi_j, \end{eqnarray*}$

(2.38)$\begin{eqnarray*} &&\frac{{\rm d}\Psi_{j}}{{\rm d}t}=L_{h,p}^\beta \Phi_j-\Phi_{j}+P_{j}^2+Q_{j}^2. \end{eqnarray*}$

定理 2.3 分数阶 KGS 方程组 (2.1)-(2.2) 的半离散格式 (2.35)-(2.38) 可写为如下有限维 Hamilton 系统

(2.39)$\begin{eqnarray*} \frac{{\rm d}Z}{{\rm d}t}=f(Z)=S_J\nabla H(Z), \end{eqnarray*}$

其中

$\begin{eqnarray*} &&P=(P_0,P_1,\cdots, P_{J-1}),Q=(Q_0,Q_1,\cdots, Q_{J-1}),\\ &&\Phi=(\Phi_0,\Phi_1,\cdots, \Phi_{J-1}),\Psi=(\Psi_0,\Psi_1,\cdots, \Psi_{J-1}),\\ &&Z=(P_0,P_1,\cdots, P_{J-1},Q_0,Q_1,\cdots, Q_{J-1},\Psi_0,\Psi_1,\cdots, \Psi_{J-1},\Phi_0,\Phi_1,\cdots, \Phi_{J-1}), \end{eqnarray*}$

$ S_J=\left[\begin{array}{ccccc} \textbf{0}&\textbf{0}&I_{J\times J}&\textbf{0}\\ \textbf{0}&\textbf{0}&\textbf{0}&I_{J\times J}\\ -I_{J\times J}&\textbf{0}&\textbf{0}&\textbf{0}\\ \textbf{0}&-I_{J\times J}&\textbf{0}&\textbf{0}\\ \end{array}\right], $

$H(Z)=\langle\frac{1}{2}L_{h,p}^\alpha P, P\rangle+\langle\frac{1}{2}L_{h,p}^\alpha Q, Q\rangle+\langle-L_{h,p}^\beta \Phi,\Phi\rangle+\langle\Psi,\Psi\rangle-\langle\Phi,\Phi\rangle+\frac{1}{2}\sum\limits_{j=0}^{J-1}(P_j^2\Phi_j+Q_j^2\Phi_j).$

该系统满足辛和能量守恒定律

(2.40)$\begin{eqnarray*} &&\frac{{\rm d}}{{\rm d}t}\int_\Omega {\rm d}z\wedge S_J{\rm d}z{\rm d}\Omega=0, \end{eqnarray*}$

(2.41)$\begin{eqnarray*} &&\frac{{\rm d}H(Z)}{{\rm d}t}=f(Z)=\nabla H(Z)^TS_J\nabla H(Z)=0.\end{eqnarray*}$

3 分数阶 KGS 方程组全离散格式

对半离散分数阶 KGS 方程组 (2.35)-(2.38) 在时间方向采用辛中点格式, 得到分数阶 KGS 方程组 (2.1)-(2.2) 的全离散辛格式为

(3.1)$\begin{eqnarray*} &&Q_t^{n+\frac{1}{2}}=\frac{1}{2}L_{h,p}^\alpha P^{n+\frac{1}{2}} +P^{n+\frac{1}{2}}\cdot\Phi^{n+\frac{1}{2}}{,} \end{eqnarray*}$

(3.2)$\begin{eqnarray*} &&P_t^{n+\frac{1}{2}}=\frac{1}{2}L_{h,p}^\alpha Q^{n+\frac{1}{2}} +Q^{n+\frac{1}{2}}\cdot\Phi^{n+\frac{1}{2}}{,} \end{eqnarray*}$

(3.3)$\begin{eqnarray*} &&\Phi_t^{n+\frac{1}{2}}=(I\Psi^{n+\frac{1}{2}}){,} \end{eqnarray*}$

(3.4)$\begin{eqnarray*} &&\Psi_t^{n+\frac{1}{2}}=-\frac{1}{2}(L_{h,p}^\beta-I)(\Phi^{n+\frac{1}{2}})+(P^{n+\frac{1}{2}})^2+(Q^{n+\frac{1}{2}})^2{,} \end{eqnarray*}$

消去变量 $\Psi_t^{n}, \Psi_t^{n+1}$, $P^n, P^{n+1}, Q^n,Q^{n+1}$, 有

(3.5)$\begin{eqnarray*} &&{\rm i}U^{n+\frac{1}{2}}_t-\frac{1}{2}L_{h,p}^\alpha U^{n+\frac{1}{2}}+U^{n+\frac{1}{2}}\cdot \Phi^{n+\frac{1}{2}}=0, \end{eqnarray*}$

(3.6)$\begin{eqnarray*} &&\Phi^{n}_{t\overline{t}}-\frac{1}{2}L_{h,p}^\beta(\Phi^{n+\frac{1}{2}}+\Phi^{n-\frac{1}{2}})+\frac{1}{2}(\Phi^{n+\frac{1}{2}}+\Phi^{n-\frac{1}{2}})=\frac{1}{2}(|U^{n+\frac{1}{2}}|^2+|U^{n-\frac{1}{2}}|^2), \end{eqnarray*}$

(3.7)$\begin{eqnarray*} &&U_j^0=u_0(x_j), \Phi_j^0=\phi_0(x_j), (\Phi_j^0)_{\hat{t}}=\phi_1(x_j), x_j\in\Omega_h \end{eqnarray*}$

(3.8)$\begin{eqnarray*} &&U_0^n=U_J^n, \Phi_0^n=\Phi_J^n, t_n\in\bar{\Omega}_\tau. \end{eqnarray*}$

定理 3.1 分数阶 KGS 方程组的全离散格式 (3.5)-(3.8) 具有如下守恒性质

$\begin{eqnarray*} \|U^n\|^2=\|U^{n-1}\|^2\cdots =\|U^0\|^2. \end{eqnarray*}$

证计算 $U^{n+\frac{1}{2}}$ 与方程 (3.5) 的内积可以得到

(3.9)$\begin{eqnarray*} \frac{\rm i}{2\tau}\langle U^{n+1}-U^{n}, U^{n+1}+U^{n}\rangle+\frac{1}{2}\langle L_{h,p}^\alpha U^{n+\frac{1}{2}},U^{n+\frac{1}{2}}\rangle=\langle U^{n+\frac{1}{2}}\Phi^{n+\frac{1}{2}}, U^{n+\frac{1}{2}}\rangle=0. \end{eqnarray*}$

通过引理 2.8, 取上面方程的虚部有

$\|U^{n+1}\|^2=\|U^n\|^2.$

证毕.

定理 3.2 分数阶 KGS 方程组的全离散格式 (3.5)-(3.8) 的能量具有如下性质

${\rm Re}s^{n+\frac{1}{2}}=\frac{1}{\tau}(\varepsilon^{n+\frac{1}{2}}- \varepsilon^{n-\frac{1}{2}})=\frac{h}{\tau}\sum\limits_{j=0}^{J-1}|U_j^{n+\frac{1}{2}}-U_j^{n-\frac{1}{2}}|^2(\Phi_j^{n+\frac{1}{2}}-\Phi_j^{n-\frac{1}{2}}){,}$

其中

$\varepsilon^{n+\frac{1}{2}}=\|\Phi^{n+\frac{1}{2}}_t\|^2+\|\Lambda^\beta\Phi^{n+\frac{1}{2}}\|^2+\|\Phi^{n+\frac{1}{2}}\|^2+ \|\Lambda^\alpha U^{n+\frac{1}{2}}\|^2-2h\sum\limits_{j=0}^{J-1}\Phi_j^{n+\frac{1}{2}}|U_j^{n+\frac{1}{2}}|^2{.}$

证通过方程 (3.5) 可以得到

(3.10)$\begin{eqnarray*} &&{\rm i}(U^{n+\frac{1}{2}}_t+U^{n-\frac{1}{2}}_t)-\frac{1}{2}L_{h,p}^\alpha (U^{n+\frac{1}{2}}+U^{n-\frac{1}{2}})+(U^{n+\frac{1}{2}}\cdot \Phi^{n+\frac{1}{2}}+U^{n-\frac{1}{2}}\cdot \Phi^{n-\frac{1}{2}})=0. \end{eqnarray*}$

计算 $U^{n+\frac{1}{2}}_t+U^{n-\frac{1}{2}}_t$ 与方程 (3.10) 的内积可以得到

$\begin{eqnarray*} &&\frac{\rm i}{\tau^2}\|U^{n+1}-U^{n-1}\|^2-\frac{1}{\tau}\langle L_{h,p}^\alpha (U^{n+\frac{1}{2}}+U^{n-\frac{1}{2}}),U^{n+\frac{1}{2}}-U^{n-\frac{1}{2}}\rangle\\ &&+\frac{2}{\tau}\langle U^{n+\frac{1}{2}}\cdot \Phi^{n+\frac{1}{2}}+U^{n-\frac{1}{2}}\cdot \Phi^{n-\frac{1}{2}},U^{n+\frac{1}{2}}-U^{n-\frac{1}{2}}\rangle=0. \end{eqnarray*}$

通过直接推导可以得到

$\begin{align*} &\frac{\rm i}{\tau^2}\|U^{n+1}-U^{n-1}\|^2-\frac{1}{\tau}\langle L_{h,p}^\alpha (U^{n+\frac{1}{2}}+U^{n-\frac{1}{2}}),U^{n+\frac{1}{2}}-U^{n-\frac{1}{2}}\rangle\\ &+\frac{2}{\tau}h\sum\limits_{j=0}^{J-1}(\Phi_j^{n+\frac{1}{2}}|U_j^{n+\frac{1}{2}}|^2-\Phi_j^{n-\frac{1}{2}}|U_j^{n-\frac{1}{2}}|^2)\\ &+\frac{2}{\tau}h\sum\limits_{j=0}^{J-1}(\Phi_j^{n-\frac{1}{2}}U_j^{n-\frac{1}{2}}\overline{U_j^{n+\frac{1}{2}}}-\Phi_j^{n+\frac{1}{2}}U_j^{n+\frac{1}{2}}\overline{U_j^{n-\frac{1}{2}}})=0. \end{align*}$

取上面方程的实部可以得到

(3.11)$\begin{align*} &\frac{1}{\tau}[(\|\Lambda^\alpha U^{n+\frac{1}{2}}\|^2+2h\sum\limits_{j=0}^{J-1}\Phi_j^{n+\frac{1}{2}}|U_j^{n+\frac{1}{2}}|^2)- (\|\Lambda^\alpha U^{n-\frac{1}{2}}\|^2+2h\sum\limits_{j=0}^{J-1}\Phi_j^{n-\frac{1}{2}}|U_j^{n-\frac{1}{2}}|^2)]\notag \\ &-\frac{2}{\tau}\mbox{Re}[h\sum\limits_{j=0}^{J-1}(\Phi_j^{n-\frac{1}{2}}U_j^{n-\frac{1}{2}}\overline{U_j^{n+\frac{1}{2}}}-\Phi_j^{n+\frac{1}{2}}U_j^{n+\frac{1}{2}}\overline{U_j^{n-\frac{1}{2}}})]=0. \end{align*}$

计算 $\Phi^{n+\frac{1}{2}}_t+\Phi^{n-\frac{1}{2}}_t$ 与方程 (3.6) 的内积可以得到

$\begin{align*} &\frac{1}{\tau}[\langle\Phi^{n+\frac{1}{2}}_t+\Phi^{n-\frac{1}{2}}_t,\Phi^{n+\frac{1}{2}}_t-\Phi^{n-\frac{1}{2}}_t\rangle-\frac{1}{2}\langle(L_{h,p}^\beta+I)(\Phi^{n+\frac{1}{2}}+\Phi^{n-\frac{1}{2}}),\Phi^{n+\frac{1}{2}}-\Phi^{n-\frac{1}{2}} \rangle\\ &-h\sum\limits_{j=0}^{J-1}(|U_j^{n+\frac{1}{2}}|^2+|U_j^{n-\frac{1}{2}}|^2)(\Phi_j^{n+\frac{1}{2}}-\Phi_j^{n-\frac{1}{2}})] \end{align*}$

通过引理 2.8 得到

$\langle(L_{h,p}^\beta+I)\Phi^{n+\frac{1}{2}},\Phi^{n+\frac{1}{2}}\rangle=\|\Lambda^\beta\Phi^{n+\frac{1}{2}}\|^2+\|\Phi^{n+\frac{1}{2}}\|^2.$

然后

(3.12)$\begin{align*} &\frac{1}{\tau}[(\|\Phi^{n+\frac{1}{2}}_t\|^2+\|\Lambda^\beta\Phi^{n+\frac{1}{2}}\|^2+\|\Phi^{n+\frac{1}{2}}\|^2)-(\|\Phi^{n-\frac{1}{2}}_t\|^2+\|\Lambda^\beta\Phi^{n-\frac{1}{2}}\|^2+\|\Phi^{n-\frac{1}{2}}\|^2)\notag\\ =&\frac{h}{\tau}\sum\limits_{j=0}^{J-1}(|U_j^{n+\frac{1}{2}}|^2+|U_j^{n-\frac{1}{2}}|^2)(\Phi_j^{n+\frac{1}{2}}-\Phi_j^{n-\frac{1}{2}})] \end{align*}$

注意到方程 (3.11)-(3.12) 可以得到

$\begin{align*} \frac{1}{\tau}(\varepsilon^{n+\frac{1}{2}}- \varepsilon^{n-\frac{1}{2}})=&\frac{h}{\tau}\sum\limits_{j=0}^{J-1}[(|U_j^{n+\frac{1}{2}}|^2+|U_j^{n-\frac{1}{2}}|^2)(\Phi_j^{n+\frac{1}{2}}-\Phi_j^{n-\frac{1}{2}})\\ &+\mbox{Re}(\Phi_j^{n-\frac{1}{2}}U_j^{n-\frac{1}{2}}\overline{U_j^{n+\frac{1}{2}}}-\Phi_j^{n+\frac{1}{2}}U_j^{n+\frac{1}{2}}\overline{U_j^{n-\frac{1}{2}}})]\\ =&\sum\limits_{j=0}^{J-1}|U_j^{n+\frac{1}{2}}-U_j^{n-\frac{1}{2}}|^2(\Phi_j^{n+\frac{1}{2}}-\Phi_j^{n-\frac{1}{2}}). \end{align*}$

证毕.

4 数值例子

数值格式 (3.5)-(3.6) 可以表示为

$\begin{align*} &\frac{\rm i}{\tau}(U^{n+1}-U^n)-\frac{1}{4}L_{h,p}^\alpha (U^{n+1}+U^n)+\frac{1}{4}(U^{n+1}+U^n)\cdot (\Phi^{n+1}+\Phi^n)=0, \\ &\frac{1}{\tau^2}(\Phi^{n+1}-2\Phi^{n}+\Phi^{n})-\frac{1}{4}L_{h,p}^\beta(\Phi^{n+1}+\Phi^{n-1})+\frac{1}{4}(\Phi^{n+1}+\Phi^{n-1})\\ =&\frac{1}{2}(|\frac{U^{n+1}+U^n}{2}|^2+|\frac{U^{n}+U^{n-1}}{2}|^2). \end{align*}$

上面的数值格式为非线性格式, 在数值求解过程中需要构造迭代算法. 假设$(U^n, \Phi^{n}), n=0,1,2\cdots$ 已经得到. $(U^{n+1}, \Phi^{n+1})$ 通过下面迭代算法得到

$\begin{align*} &\frac{\rm i}{\tau}(U^{n+1(s+1)}-U^n)-\frac{1}{4}L_{h,p}^\alpha (U^{n+1(s+1)}+U^n)+\frac{1}{4}(U^{n+1(s)}+U^n)\cdot (\Phi^{n+1(s)}+\Phi^n)=0, \\ &\frac{1}{\tau^2}(\Phi^{n+1(s+1)}-2\Phi^{n}+\Phi^{n})-\frac{1}{4}L_{h,p}^\beta(\Phi^{n+1(s+1)}+\Phi^{n-1})+\frac{1}{4}(\Phi^{n+1(s+1)}+\Phi^{n-1})\notag\\ =&\frac{1}{2}(|\frac{U^{n+1(s)}+U^n}{2}|^2+|\frac{U^{n}+U^{n-1}}{2}|^2). \end{align*}$

当 $\alpha=2,\beta=2, m=1$, 系统 (2.1)-(2.4) 表示为经典的 KGS 方程组, 并具有以下孤立波解^[2]

$\begin{eqnarray*} &&u(x,t,v)=\frac{3\sqrt{2}}{4\sqrt{1-v^2}}\mbox{sech}^2\frac{1}{2\sqrt{1-v^2}}(x-vt-x_0)\cdot\exp({\rm i}(vx+\frac{1-v^2+v^4}{2(1-v^2)}t)),\\ &&\phi(x,t,v)=\frac{3}{4(1-v^2)}\mbox{sech}^2\frac{1}{2\sqrt{1-v^2}}(x-vt-x_0), \end{eqnarray*}$

其中, $v$ 是波的传播速度, $x_0$ 是初始相位. 考虑初值 $(v=0.8, x_0=-10)$

(4.1)$\begin{eqnarray*} &&u_0=\frac{3\sqrt{2}}{4\sqrt{1-v^2}}\mbox{sech}^2\frac{1}{2\sqrt{1-v^2}}\cdot(x-x_0)\exp({\rm i}vx), \end{eqnarray*}$

(4.2)$\begin{eqnarray*} &&\phi_0=\frac{3}{4(1-v^2)}\mbox{sech}^2\frac{1}{2\sqrt{1-v^2}}(x-x_0). \end{eqnarray*}$

本文在时间上采用辛中点格式, 在空间上采用数值格式 I (二阶中心差分格式), 数值格式 II (四阶中心差分格式).

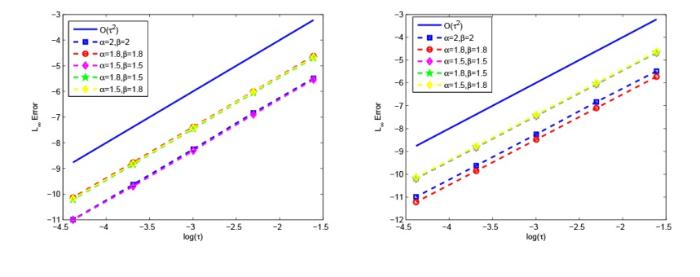
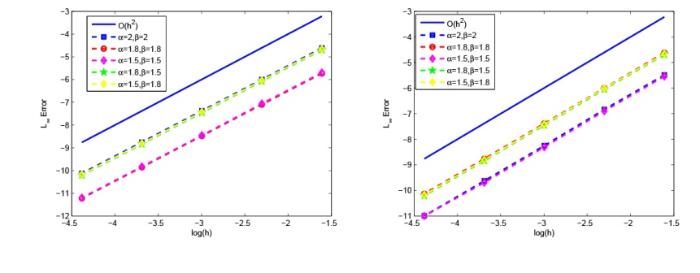
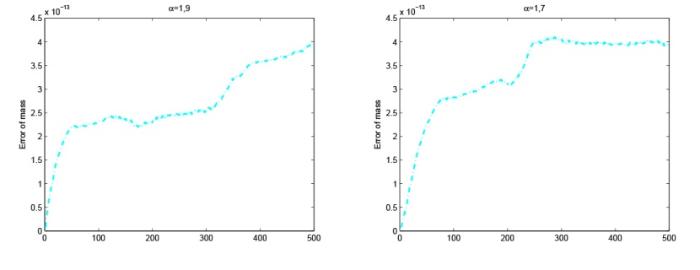
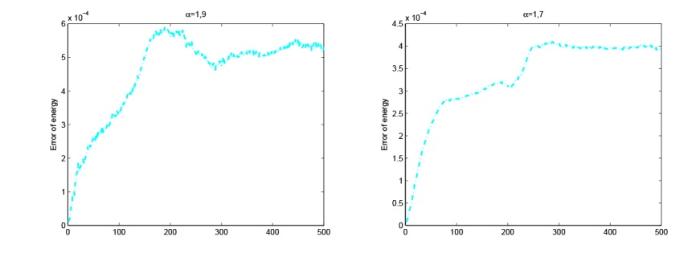
首先, 我们验证数值格式的时间和空间的误差和收敛阶, 图1-3 分别给出了不同 $\alpha$, $\beta$ 数值格式的时间和空间 $l^\infty$ 范数误差和收敛阶. 对于 $\alpha, \beta \neq 2 $, 通过细网格和小时间步长 $\displaystyle h = 0.0001, \tau=0.0001$ 得到 $u, \phi $ 数值精确解. 通过图1-3 的数值结果, 我们发现数值格式 I 在空间上是二阶的, 数值格式 II 在空间上是四阶的, 数值格式 I,II 在时间上都是二阶的. 第二, 检测数值格式的离散守恒律, 图4-5 给出了离散质量和离散能量在不同的 $\alpha, \beta $ 的值, 我们发现数值格式 I、II 很好地保持离散质量守恒, 然而不保持能量守恒定律, 但是它们的残差很小.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 时间误差和收敛阶:左 $u$；右 $\phi$

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 空间误差和收敛阶 (数值格式 I):左 $u$；右 $\phi$

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 空间误差和收敛阶 (数值格式 II):左 $u$；右 $\phi$

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 质量误差图, $ \beta=2$

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 能量误差图, $ \beta=2$

最后, 我们考虑单孤立波 (4.1)-(4.2) 和下面两个孤立波的碰撞情况

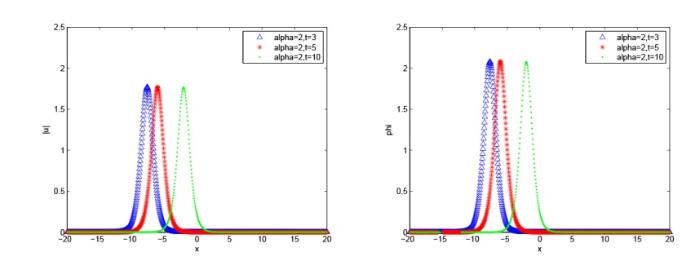
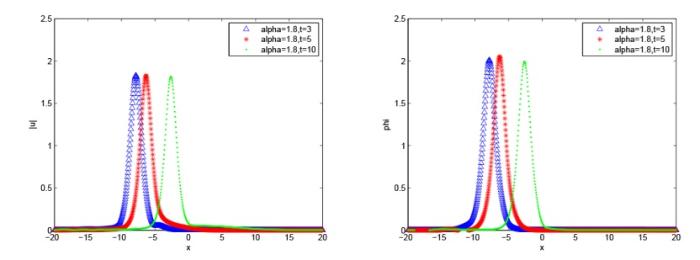
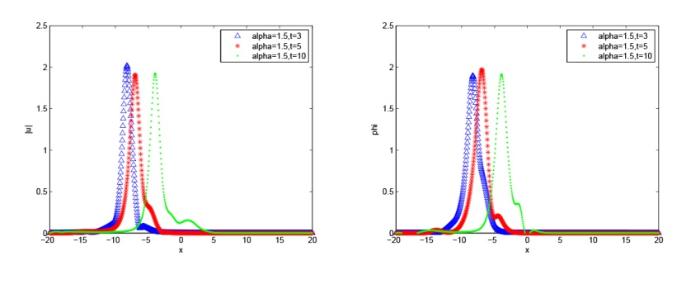
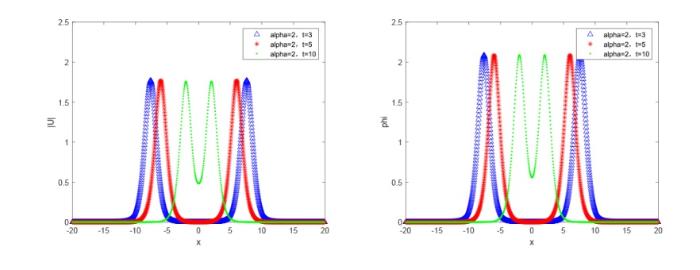
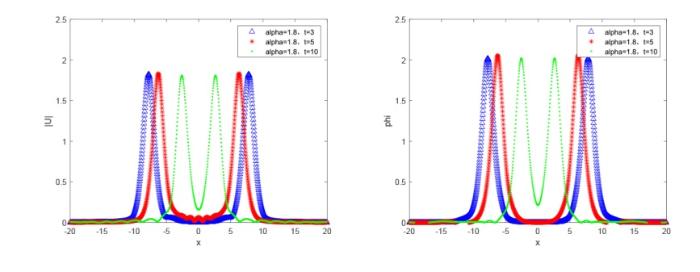
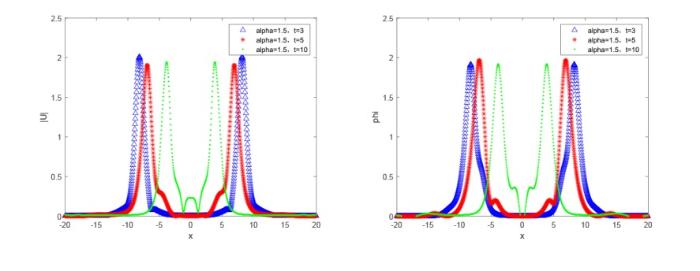
$\begin{equation*} u_0=u(x-p_1,0,v_1)+u(x-p_2,0,v_2), \\ \phi_0=\phi(x-p_1,0,v_1)+\phi(x-p_2,0,v_2). \end{equation*}$

选取 $(p_1=10, p_2=10, v_1=0.8, v_2=-0.8)$. 取定参数 $x\in[ -20,20], \tau=0.1, h =0.1$, 对分数阶 KGS 系统的孤立波进行了数值模拟. 图6-8 给出了不同分数阶 $\alpha$ 在不同时间单孤立波数值解的波形, 图9-11 给出了不同分数阶 $\alpha$ 在不同时间孤立波碰撞数值解的波形. 从图6-8 中, 发现 $\alpha$ 阶会影响孤立波的形状和振幅, 当 $\alpha $ 变小时, 孤子的形状变化更快, 振幅变化更大. 此外, 我们还发现孤立波在周围出现了一些小的振荡. 从图9-11 中, 发现 $\alpha$ 阶也会影响孤立波的形状和振幅, 当 $\alpha $ 变小时, 孤立波碰撞时间将推迟. 对于不同的分数阶 $\beta$ 也会类似的影响孤立波.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 数值解波形图, $\alpha=2, \beta=2$

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 数值解波形图, $\alpha=1.8, \beta=2$

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 数值解波形图, $\alpha=1.5, \beta=2$

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 数值解波形图, $\alpha=2, \beta=2$

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 数值解波形图, $\alpha=1.8, \beta=2$

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 数值解波形图, $\alpha=1.5, \beta=2$

5 结论

本文研究分数阶 KGS 方程组的辛差分格式. 首先, 基于分数阶中心差分格式对分数阶 KGS 方程组进行空间离散, 得到的半离散系统是一个有限维 Hamilton 系统. 接着, 利用辛中点格式对时间进行离散得到全离散格式, 并且对该格式进行了收敛性分析, 其收敛阶为 $O(\tau^2+h^4)$. 最后, 通过数值实验验证了该数值格式的有效性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Feng

, Qin

Symplectic Geometric Algorithms for Hamiltonian Systems. Berlin: Springer, 2009