空间分数阶 KGS 方程组的辛差分格式

摘要/Abstract

摘要：

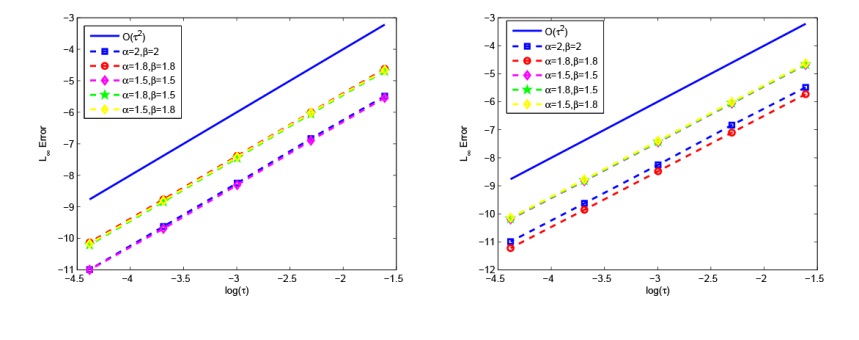
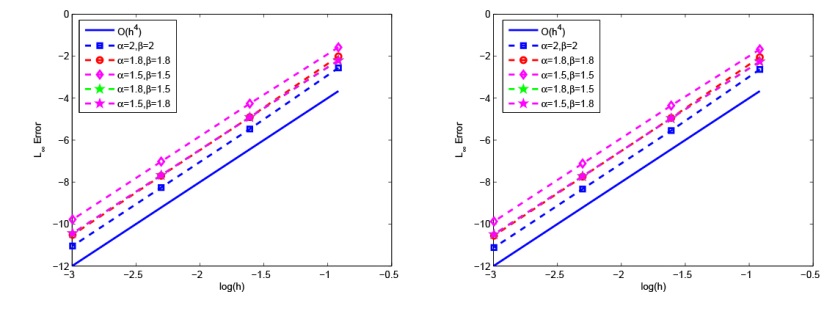
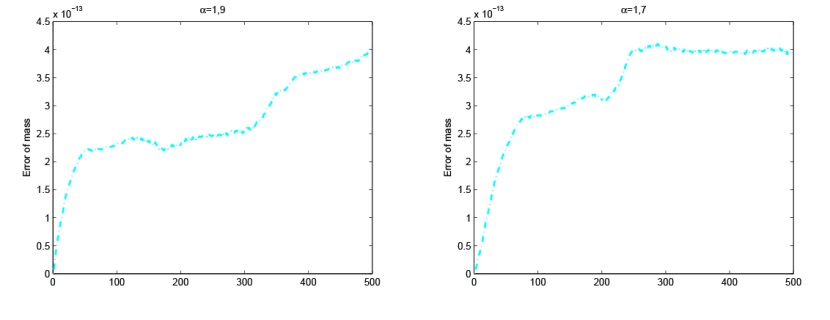
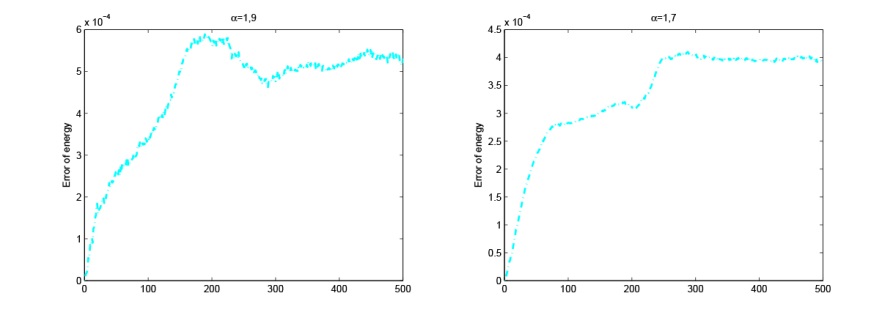
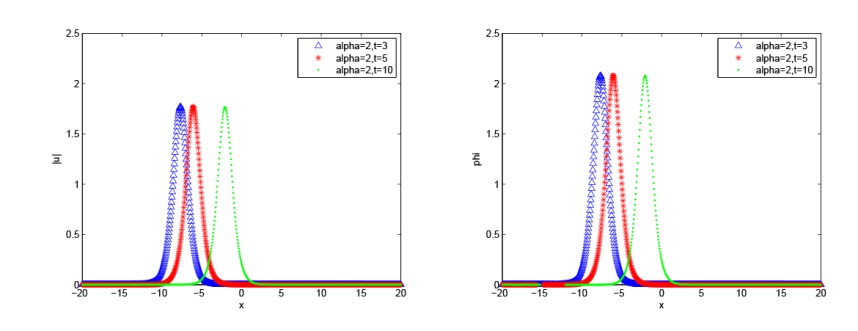
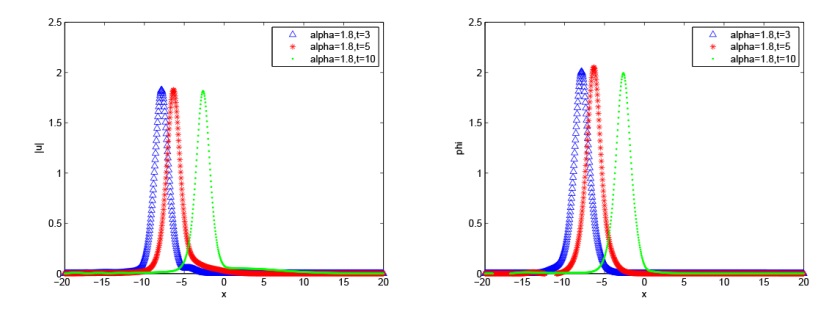
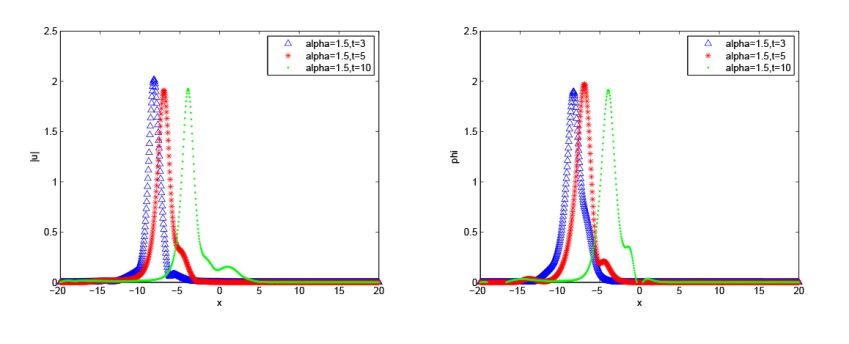
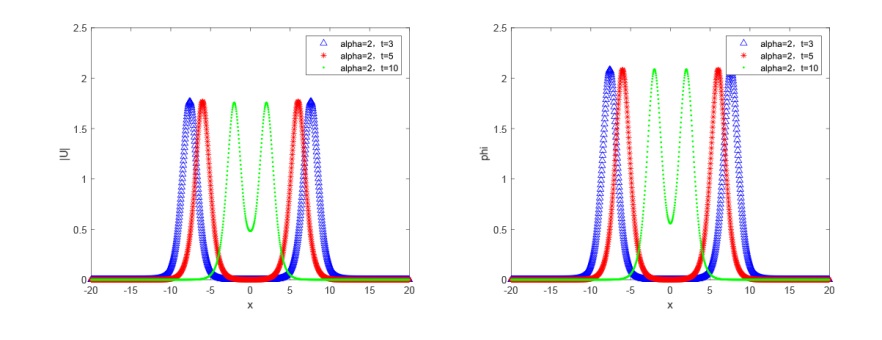
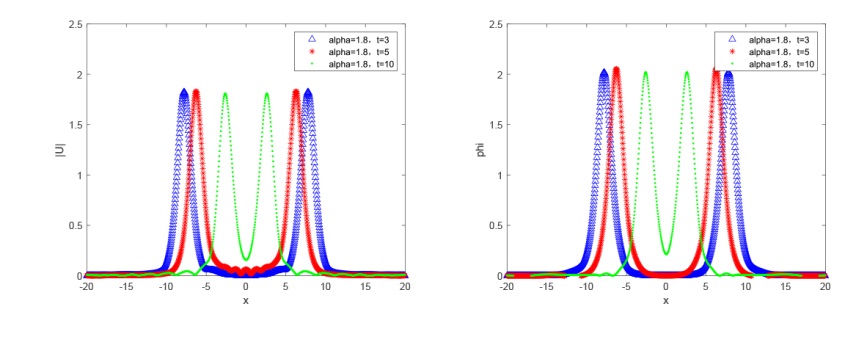
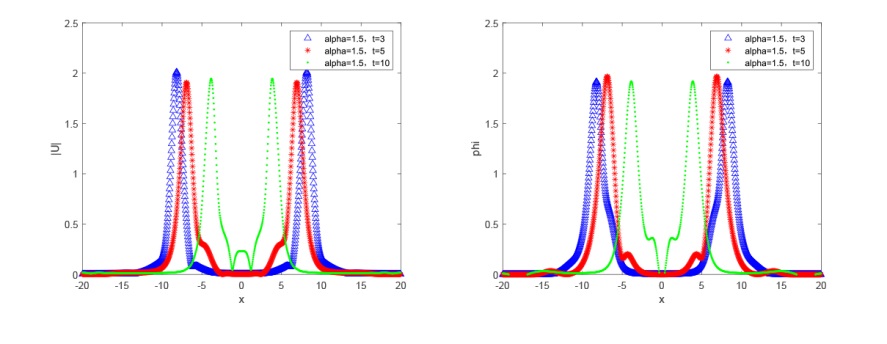
该文研究分数阶 KGS 方程组的辛差分格式. 首先, 作者给出了无穷维分数阶 Hamilton 系统, 并将 KGS 方程组转化为 Hamilton 系统. 然后, 基于分数阶中心差分格式对分数阶 KGS 方程组进行空间离散, 得到的半离散系统是一个有限维 Hamilton 系统. 接着, 利用辛中点格式对时间进行离散得到全离散格式, 并且对该格式进行了守恒性分析. 最后, 通过数值实验验证了该数值格式的有效性.

关键词: 分数阶 KGS 方程组, 守恒格式, 辛格式, 收敛性

Abstract:

In the paper, the symplectic-preserving schemes are presented for fractional Klein-Gordon-Schrödinger equations. First, we give the infinite-dimensional Hamilton with fractional Laplacian operator and conservation laws, and change the above quantum mechanical equations into Hamilton system. We apply the central finite difference schemes to discrete Klein-Gordon-Schrödinger in space, and yield a large Hamilton ordinary differential system. Second, we use the midpoint rule in time to Hamiltonian ordinary differential system, and obtain a symplectic approximation of the these equations. Moreover, we analyze the conservation of the numerical scheme. Finally, we give numerical experiments to show the verify the efficiency of the conservative finite difference scheme.

Key words: Fractional Klein-Gordon-Schrödinger equations, Conservative scheme, Symplectic scheme, Convergence

中图分类号:

O242.2

王俊杰. 空间分数阶 KGS 方程组的辛差分格式[J]. 数学物理学报, 2024, 44(5): 1319-1334.

Wang Junjie. Symplectic Difference Scheme for the Space Fractional KGS Equations[J]. Acta mathematica scientia,Series A, 2024, 44(5): 1319-1334.

图/表 11

图1

图2

图3

图4

图5

图6

图7

图8

图9

图10

图11

参考文献 36

[1]	Feng K, Qin M. Symplectic Geometric Algorithms for Hamiltonian Systems. Berlin: Springer, 2009
[2]	Channel P, Scovel C. Symplectic integration of Hamiltonian systems. Nonlinearity, 1990, 3: 231-259 doi: 10.1088/0951-7715/3/2/001
[3]	Liu X, Qi Y, He J, Ding P. Recent progress in symplectic algorithms for use in quantum systems. Communications in Computational Physcis, 2007, 2(1): 1-53
[4]	Mclachlan R. Symplectic integration of Hamiltonian wave equations. Numerische Mathematik, 1994, 66: 465-492
[5]	Sanz-Serna J, Calvo M. Numerical Hamiltonian Problems. London: Chapman and Hall, 1994
[6]	Hairer E, Lubich C, Wanner G. Geometric Numerical Integration: Structure Preserving Algorithms for Ordinary DifferentialEquations. Berlin: Springer-Verlag, 2002
[7]	Bridges T, Reich S. Numerical methods for Hamiltonian PDEs. Journal of Physics A Mathematical and General, 2006, 39: 5287-5320
[8]	Gong Y, Cai J, Wang Y. Some new structure-preserving algorithms for general multi-symplectic formulations of Hamiltonian PDEs. Journal of Computational Physics, 2014, 279: 80-102
[9]	Bridges T. Multi-symplectic structures and wave propagation. Mathematical Proceedings of the Cambridge Philosophical Society, 1997, 121: 147-190
[10]	Chen Y, Sun Y, Tang Y. Energy-preserving numerical methods for Landau-Lifshitz equation. Journal of Physics A Mathematical and Theoretical, 2011, 44(29): 295207
[11]	Kong L, Hong J, Zang J. Splitting multi-symplectic integrators for Maxwell's equation. Journal of Computational Physics, 2010, 229: 4259-4278
[12]	Reich S. Multi-symplectic Runge-Kutta collocation methods for Hamiltonian wave equations. Journal of Computational Physics, 2000, 157: 473-499
[13]	Ober-Blöbaum S. Galerkin variational integrators and modified symplectic Runge-Kutta methods. IMA Journal of Numerical Analysis, 2017, 37: 375-406
[14]	Mei L, Wu X. Symplectic exponential Runge-Kutta methods for solving nonlinear Hamiltonian systems. Journal of Computational Physics, 2017, 338: 567-584
[15]	Wang P, Hong J, Xu D. Construction of symplectic Runge-Kutta methods for stochastic Hamiltonian systems. Computer Physics Communications, 2017, 21(1): 237-270
[16]	Guo B, Pu X, Huang F. Fractional Partial Differential Equations and Their Numerical Solutions. Beijing: World Scientific Publishing, 2011
[17]	Li C P, Zeng F H. Numerical Methods for Fractional Calculus. New York: CRC Press, 2015
[18]	孙志高, 高广花. 分数阶偏微分方程的有限差分方法. 北京: 科学出版社, 2015
	Sun Z G, Gao G H. Finite Difference Methods for Fractional-order Differential Equations. Beijing: Science Press, 2015
[19]	刘发旺, 庄平辉, 刘青霞. 分数阶偏微分方程数值方法及其应用. 北京: 科学出版社, 2015
	Liu F W, Zhuang P H, Liu Q X. Numerical Methods and Their Applications of Fractional Partial Differential Equations. Beijing: Science Press, 2015
[20]	Wang P, Huang C, Zhao L. Point-wise error estimate of a conservative difference scheme for the fractional Schrödinger equation. Journal of Computational and Applied Mathematics, 2016, 306: 231-247
[21]	Wang D, Xiao A, Yang W. Crank-Nicolson difference scheme for the coupled nonlinear Schrödinger equations with the Riesz space fractional derivative. Journal of Computational Physics, 2013, 242: 670-681
[22]	Zhao X, Sun Z, Hao Z. A fourth-order compact ADI scheme for two-dimensional nonlinear space fractional Schrödinger equation. SIAM Journal on Scientific Computing, 2014, 36(6): A2865-A2886
[23]	Bueno-Orovio A, Kay D, Burrage K. Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numerical Mathematics, 2014, 54(4): 937-954
[24]	Pindza E, Owolabi K. Fourier spectral method for higher order space fractional reaction-diffusion equations. Commun Nonlinear Sci Numer Simulat, 2016, 40: 112-128
[25]	Wang J. High-order conservative schemes for the space fractional nonlinear Schrödinger equation. Applied Numerical Mathematics, 2021, 165: 248-269
[26]	Gao G, Sun Z. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. Journal of Computional Physics, 2014, 259: 33-50
[27]	Alikhanov A. A new difference for the time fractional diffusion equation. J Comput Phys, 2015, 280: 424-438
[28]	Jiang S, Zhang J, Zhang Q, Zhang Z. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Communications in Computational Physics, 2017, 21(3): 650-678
[29]	Stynes M, O'Riordan E, Gracia J L. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM Journal on Numerical Analysis, 2017, 55: 1057-1079
[30]	Jin B, Lazarov R, Pasciak J, Zhou Z. Error analysis of semidiscrete finite element methods for inhomogeneous time-fractional diffusion. IMA Journal of Numerical Analysis, 2015, 35(2): 561-582
[31]	Jin B, Lazarov R, Zhou Z. Two fully discrete schemes for fractional diffusion and diffusion-wave equations with nonsmooth data. SIAM Journal on Scientific Computing, 2016, 38(1): A146-A170
[32]	Yang Y, Chen Y, Huang Y, Wei H. Spectral collocation method for the time-fractional diffusion-wave equation and convergence analysis. Computational & Applied Mathematics, 2017, 73: 1218-1232
[33]	Xiao A, Wang J. Symplectic scheme for the Schrödinger equation with fractional Laplacian. Applied Numerical Mathematics, 2019, 146: 469-487
[34]	Wang J. Symplectic-preserving Fourier spectral scheme for space fractional Klein-Gordon-Schrödinger equations. Numerical Methods for Partial Differential Equations, 2021, 37: 1030-1056
[35]	Wang P, Huang C. Structure-preserving numerical methods for the fractional Schrödinger equation. Applied Numerical Mathematics, 2018, 129: 137-158
[36]	Celik C. Duman M. Crank-Nicolson method for the fractional diffusion equation with the Riesz fractional derivative. Journal of Computational Physics, 2012, 231: 1743-1750