1 引言
在 LBM 的许多模型中, 使用 Bhatnagar-Gross-Krook (BGK) 碰撞算子的单松弛时间 (SRT) 模型具有更简单的碰撞项, 是目前应用最广泛的一种 LB 模型[8,9]. 然而, 该模型在模拟高雷诺数流时变得不稳定[10]. 为此, D'Humieres 建立了MRT-LB 模型[11], 在 MRT-LB 模型中, 碰撞过程在力矩空间中进行, 不同的弛豫时间对应不同的物理变量. MRT-LB 模型的数值稳定性和精度远远优于 SRT-LB 模型[12], 而且该模型提供了更丰富的流场物理信息. 柴振华等[13] 利用 Chapman-Enskog 多尺度展开方法、Mallwell 迭代、直接 Taylor 展开方法和递推方程方法从 LB 方程出发恢复出了 Navier-Stokes 方程. MRT-LB 模型已被广泛用于模拟流动, 尤其是高雷诺数流动[14,15]. 景何仿等人[16] 改进 MRT-LBM 模型, 并将其应用于刚性植被明渠流场的数值模拟. 张巧玲等人[17] 应用 MRT-LBM 模拟了三维曲面腔的流动, 结果表明较少腔角的几何形状增强了稳定性. 由于传统的数值模拟方法不能稳定地模拟高雷诺数下的流动, 因此对于高雷诺数下的流动研究较少. 最近, 张凯等人[18] 将 LES 思想引入到 MRT 中模拟了雷诺数在 500-10000 的方腔流. 已有研究表明随着雷诺数的增大腔内流动会进入到周期性状态[19], 但对方腔内各流态的特征及跃迁临界值的研究较少. 然而, 当大单网格雷诺数很高时, 如果不增加额外的工作量, MRT-LB 模型就会变得不稳定[20]. 因此, 在这项研究中, 将 MRT-LB 模型结合粘度抵消 (VC) 方法来解决这个问题.
Cheng 等人提出一种粘度抵消 (VC) 方法[21,22], 其主要思想是在模拟具有较小粘度的实际流动中引入较大粘度所对应的人工粘度, 然后通过在方程中添加一个外力项来抵消该粘度, 从而稳定地模拟粘度较小的实际流动, 用于提高 SRT-LB 模型在高雷诺数流动模拟中的稳定性[21]. 文献中已证实 MRT-LB 模型比 SRT-LB 模型具有更好的稳定性和准确性, 因此将 VC 方法引入 MRT-LB 模型可以获得更好的性能[22]. 但 MRC-VC 方法可以模拟的最大雷诺数还需要进一步探究, 故本研究将利用 MRT-VC 方法研究雷诺数为 200-500000 的流动问题, 并将模拟结果与经典数值算例进行对比分析. 此外, 还重点研究了方腔流的几种流态以及不同流态之间的跃迁雷诺数临界值.
2 数学模型与数值算法
2.1 格子玻尔兹曼方法
在不失去一般性的情况下, 我们考虑了具有 MRT 碰撞算子的二维九速 (D2Q9) 模型[23]
其中, 离散速度
矩空间的平衡分布函数
松弛变换矩阵
D2Q9 的松弛参数取
外力项
其中
上式中,
2.2 粘度抵消法
在高雷诺数的条件下, 流动的粘度较低, 数值模拟中的小耗散会导致计算不稳定. 纳维-斯托克斯 (N-S) 方程中的粘度项包含一个二阶导数, 它具有耗散作用,有助于维持数值稳定性. 在 N-S 方程的数值模拟中, 高阶截断误差在保持稳定性和精度方面发挥重要的作用. 广泛使用的 LB 模型在空间上是二阶的, 可以通过修改三阶或更高阶的截断误差项来提高稳定性, 而不会影响收敛速度. 另外, 在 LBM 中, 松弛时间不能小于 0.5, 即粘度必须为非负值. 然而, 在低粘度计算过程中, 由于数值误差的影响, 粘度误差可能为负, 这也是导致数值不稳定的重要原因之一[21].
因此, 在 N-S 方程中增加一个额外的粘度项, 如式 (2.8) 所示, 可以抵消粘度误差, 并将其作为外部强制项进行抵消处理, 这种方法可以提高数值模拟的稳定性
在公式 (2.8) 的右侧, 第二项中的
其中
其中,
需要注意的是, 对于边界附近的节点,
3 计算区域及边界条件
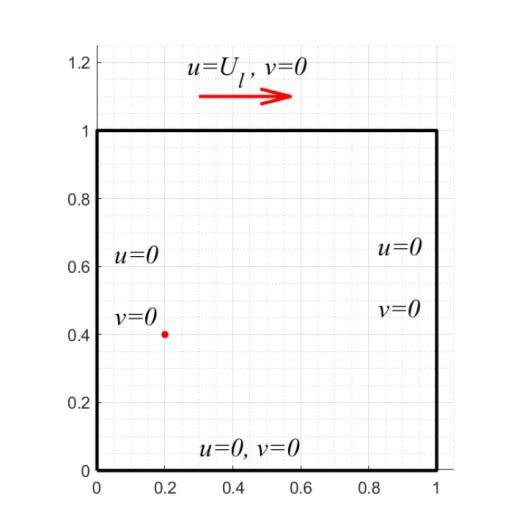
MRT-VC 模型在模拟大雷诺数方腔流时有明显的优势, 为了更好的分析不同雷诺数下的方腔内流态, 本文使用 MRT-VC 模型模拟了不同雷诺数下的顶盖驱动方腔流.
图1
在数值模拟时将参数无量纲化为格子单位. 时间步长
本文设置 MRT-VC 模型中的粘度抵消系数为 0.5, 计算得到不同雷诺数下的抵消粘度和目标粘度如表1所示
4 数值验证
为了检验 MRT-VC 能否准确稳定地模拟大雷诺数复杂涡流, 我们将其应用于顶盖驱动方腔流问题. 我们设置方腔上边界的速度
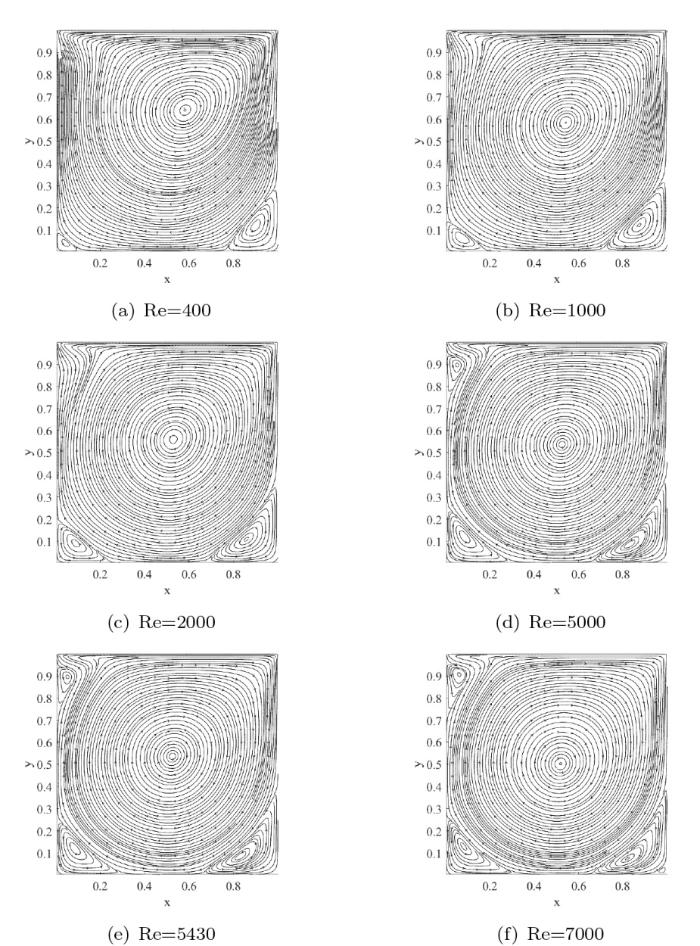
图2
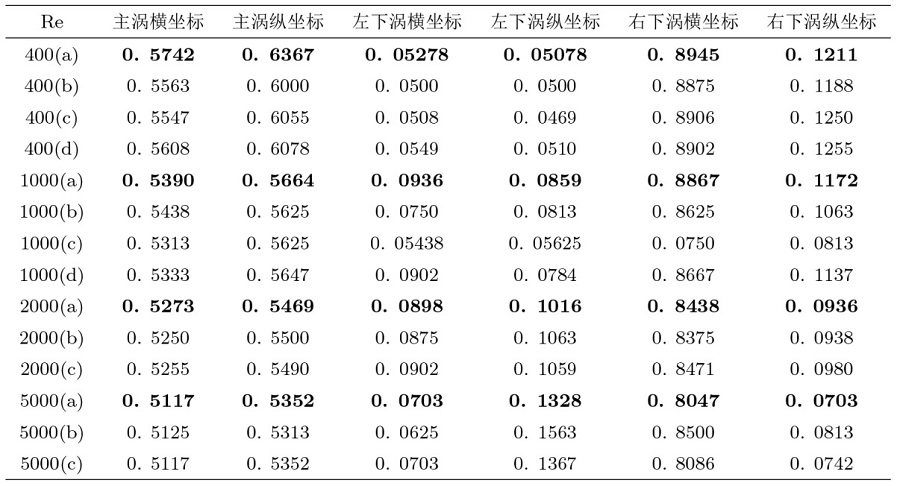
图3
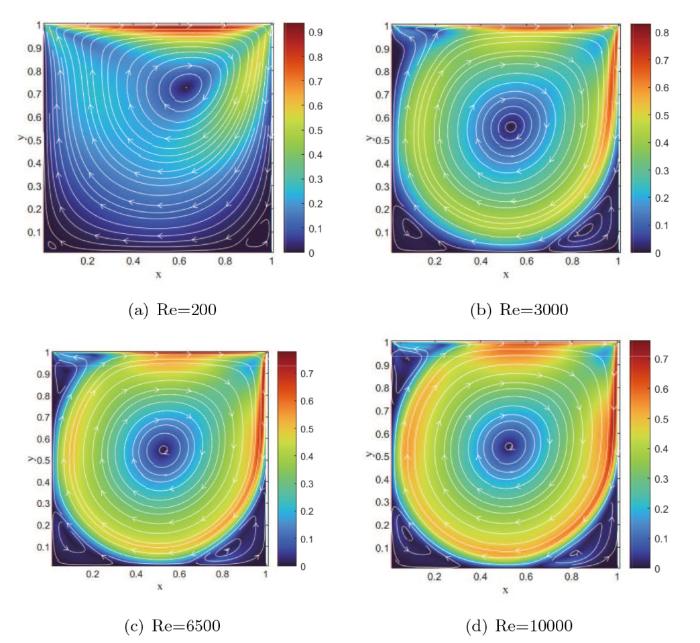
4.1 稳态流流场
矩形区域的网格数设置为
图4
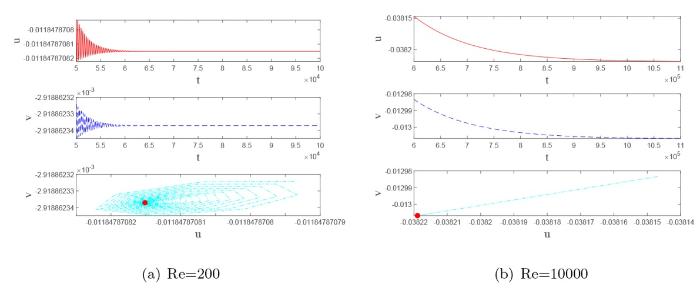
为了探究流速随时间的变化, 在计算过程中, 我们在流场中选取坐标为
图5
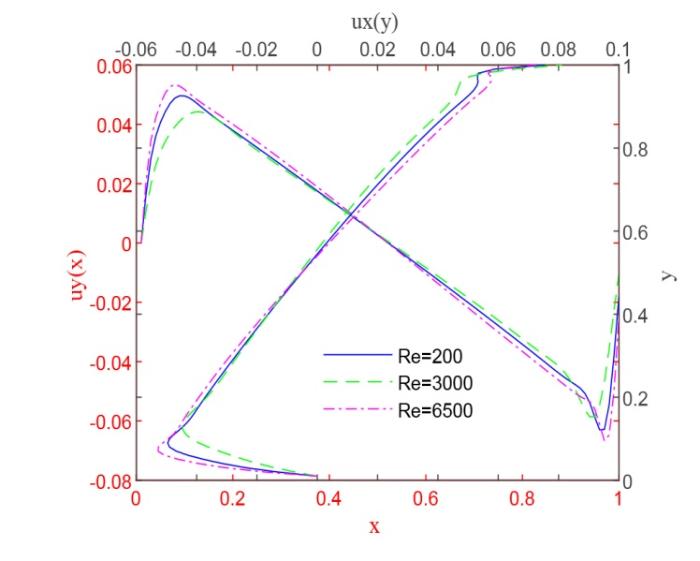
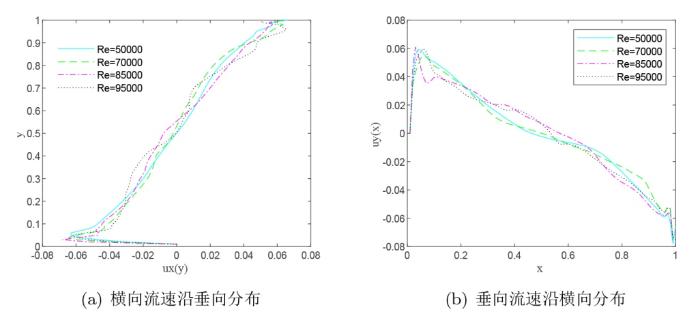
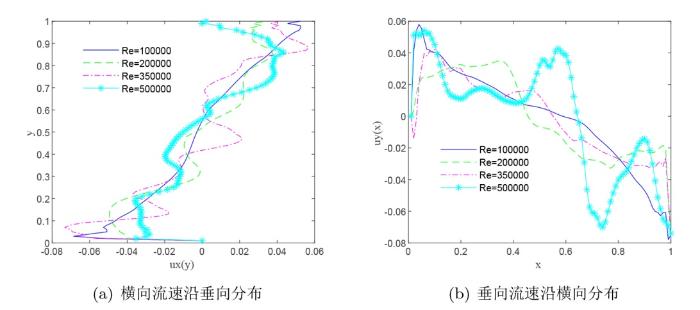
图6 为不同雷诺数下的轴向中心流速分布. 由图可见, 稳态流的轴向流速呈线性分布 (除边界附近外), 雷诺数越大, 最大流速与最小流速的差值越大.
图6
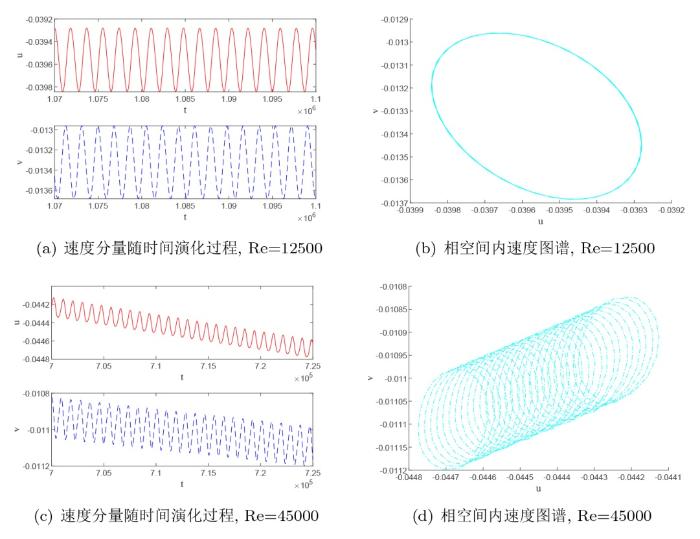
4.2 周期态流流场
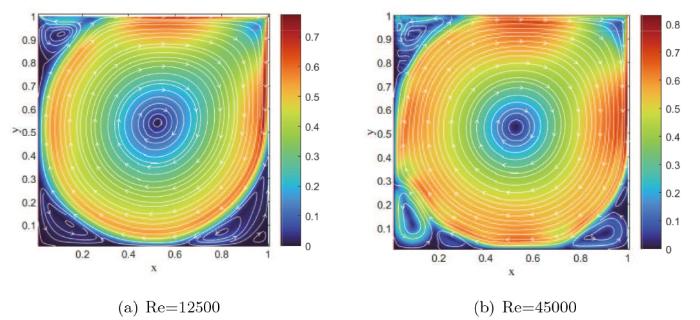
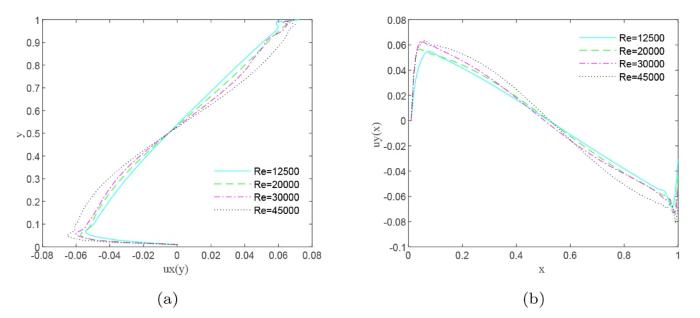
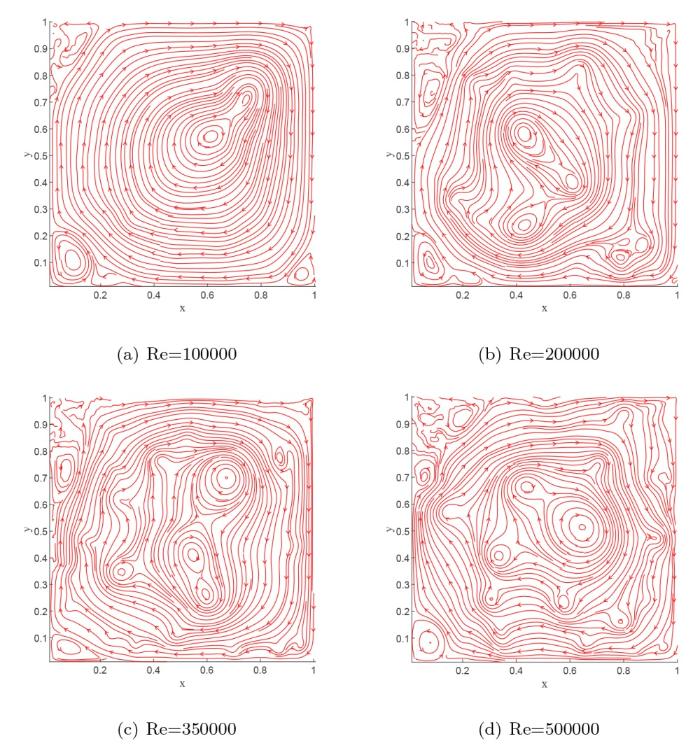
随着流动雷诺数的继续增大, 方腔内流动将不再呈现出稳定状态, 进入到周期性的变化过程中. 从图7 可以看出周期性流态的方腔内次涡尺寸较雷诺数最大的稳态流没有明显的增大, 但在右下角、左下角、左上角逐步生成了三级次涡.
图7
图8
图9
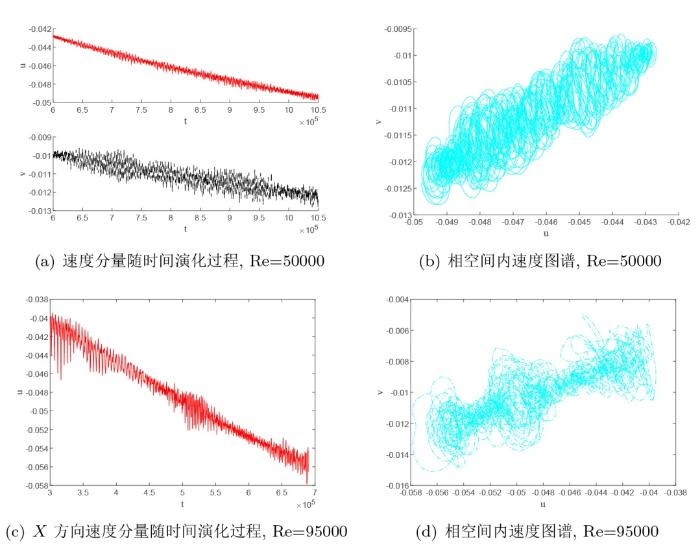
4.3 不完全混沌态流流场
图10
图11
图12
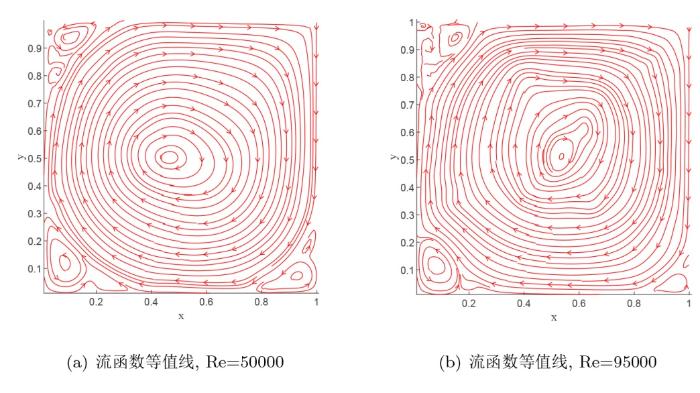
当雷诺数为 Re=50000 时, 主涡产生轻微形变, 横向速度随时间震荡式下降, 速度轨迹不规则地螺旋前进; 当雷诺数为 Re=95000 时, 主涡产生严重的形变, 有向右上角分离的趋势, 横向速度和相空间图谱的演化明显呈现出多个周期.
4.4 混沌态流流场
图13
图14
图15
综上, 在同一参数下, 方腔内流态从稳态流到周期态流的雷诺数临界值在 10000-12500 之间, 从周期态流到半周期-半稳态流的雷诺数临界值在 45000-50000 之间, 从半周期-半混沌态流到混沌流的雷诺数临界值在 95000-100000 之间.
5 结论
本文通过在 MRT-LBM 模型中引入粘度抵消方法, 建立了 D2Q9 MRT-VC 模型. 我们使用该模型对二维顶盖驱动方腔流进行了数值模拟研究, 计算了雷诺数在 200-500000 范围内流场的流动情况. 从仿真结果中, 可以得到一些重要结论
参考文献
Simulation of cavity flow by the lattice Boltzmann method
DOI:10.1006/jcph.1995.1103 URL [本文引用: 2]
Oscillatory instability of a three-dimensional lid-driven flow in a cube
The mathematical structure of the lattices of the lattice Boltzmann method
Direct simulation of fluid flow with cellular automata and the lattice-Boltzmann equation
变系数广义 KdV-Burgers 方程的格子 Boltzmann 模型
General Propagation Lattice Boltzmann Model for a Variable-Coefficient Compound KdV-Burgers Equation
Lattice Boltzmann method for fluid flows
Lattice Boltzmann and nonextensive diffusion
Lattice BGK Models for the Navier-Stokes Equations
Lattice Boltzmann method on curvilinear coordinates system: Flow around a circular cylinder
Stability analysis of lattice Boltzmann methods
Generalized lattice Boltzmann equations
Numerics of the lattice Boltzmann method: Effects of collision models on the lattice Boltzmann simulations
Multiple-relaxation-time lattice Boltzmann method for the Navier-Stokes and nonlinear conveection-diffusion equations: Modeling, analysis and elements
Lattice Boltzmann Method for Computational Fluid Dynamics
LES of turbulent square jet flow using an MRT lattice Boltzmann model
Investigation of open channel flow with unsubmerged rigid vegetation by the lattice Boltzmann method
三维曲面腔顶盖驱动流的 MRT-LBM 研究
DOI:10.19596/j.cnki.1001-246x.8447
[本文引用: 1]

采用多松弛时间格子玻尔兹曼方法(MRT-LBM)的D3Q15模型分别对长方体腔、圆柱腔、半圆柱腔、旋转双曲面腔、旋转椭球面腔、半球腔以及两种组合腔体的三维顶盖驱动腔流进行数值模拟, 比较分析各腔体内流线分布、流速等值线分布和涡心的发展, 对于典型腔体模拟不同雷诺数下的流动情况。结果表明: 在同一雷诺数下, 曲面边界不仅能消除从边界产生的次涡, 还会导致腔内主涡的分离, 增大中心纵剖面纵向回流速度; “上长方体+下半圆柱”腔内流函数分布与边界贴合度最高。当雷诺数不断增大时, 半圆柱腔内主涡逐渐分离成两个同向涡, “上圆柱+下半球”腔内始终保持着圆柱腔与半球腔内的基本流动特征; 而长方体腔内主涡涡心保持在同一高度, 次涡逐渐增强, “上长方体+下半圆柱”腔内流动愈加规则, 主涡逐渐下沉, 流速等值线分布逐渐趋于中心小、四周大。
Flow patterns in three-dimensional lid-driven cavities with curved boundary : MRT-LBM study
DOI:10.19596/j.cnki.1001-246x.8447
[本文引用: 1]

采用多松弛时间格子玻尔兹曼方法(MRT-LBM)的D3Q15模型分别对长方体腔、圆柱腔、半圆柱腔、旋转双曲面腔、旋转椭球面腔、半球腔以及两种组合腔体的三维顶盖驱动腔流进行数值模拟, 比较分析各腔体内流线分布、流速等值线分布和涡心的发展, 对于典型腔体模拟不同雷诺数下的流动情况。结果表明: 在同一雷诺数下, 曲面边界不仅能消除从边界产生的次涡, 还会导致腔内主涡的分离, 增大中心纵剖面纵向回流速度; “上长方体+下半圆柱”腔内流函数分布与边界贴合度最高。当雷诺数不断增大时, 半圆柱腔内主涡逐渐分离成两个同向涡, “上圆柱+下半球”腔内始终保持着圆柱腔与半球腔内的基本流动特征; 而长方体腔内主涡涡心保持在同一高度, 次涡逐渐增强, “上长方体+下半圆柱”腔内流动愈加规则, 主涡逐渐下沉, 流速等值线分布逐渐趋于中心小、四周大。
An improved MRT-LBM and investigation to the transition and periodicity of 2D lid-driven cavity flow with high Reynolds numbers
Fluid flow in a cavity driven by an oscillating lid-A simulation by lattice Boltzmann method
Generalized lattice Boltzmann equation with forcing term for computation of wall-bounded turbulent flows
A viscosity counteracting approach in the lattice Boltzmann BGK model for low viscosity flow: Preliminary verification
Improving the stability of the multiple-relaxation-time lattice Boltzmann method by a viscosity counteracting approach
Theory of the lattice Boltzmann method: dispersion, dissipation, isotropy, galilean invariance, and stability
Introducing unsteady non-uniform source terms into the lattice Boltzmann model
High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method
Numerical solutions of 2-D steady incompressible driven cavity flow at high Reynolds numbers
Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method