1 引言
分数阶偏微分方程主要包括椭圆型、抛物型以及双曲型三种类型. 其中, 相对于分数阶抛物和双曲方程而言, 人们对分数阶椭圆方程的研究起步相对较晚. 近年来, 基于椭圆型方程在流体力学、电磁学、几何学等学科中的应用驱动, 此类方程引起了学者们的广泛关注和研究兴趣, 尤其针对分数阶椭圆方程. 例如, 关于 Tricomi 方程、Gellerstedt 方程以及 Keldysh 方程的研究文献, 可见文献 [1⇓⇓⇓⇓-6] 等. 分数阶椭圆方程在诸如跨声速气体动力学[7], 冷等离子体数学模型[8], 社会经济系统数学建模[9]等实际科学领域中具有重要的应用价值. 此外在理论方面, 学者们也已做了相关系统的研究工作, 研究内容主要包括解的正则性、存在唯一性以及稳定性等, 参见文献 [10⇓⇓⇓-14] 等.
考虑 Tricomi-Gellerstedt-Keldysh 型分数阶椭圆方程边值问题
这里,
问题 (1.1) 是一类抽象分数阶椭圆方程边值问题. 2022 年, 文献 [16] 研究了该问题的适定性, 其包括广义解的存在唯一性和稳定性. 注意到
(i) 当
拉普拉斯方程在电磁学、流体力学以及热传导等领域中具有重要应用价值.
(ii) 当
这一方程主要应用在气体动力学、流体力学、量子力学以及几何学等实际科学领域中.
(iii) 当
Gellerstedt 方程是 Tricomi 方程的推广, 常被用于描述流体力学中的流体运动现象.
(iv) 当
此类方程主要在等离子体物理、跨音速气体动力学以及光学等实际科学领域中具有重要应用价值.
本文研究与问题 (1.1) 相关的如下反边值问题
由数据
其中,
反问题 (1.3) 是不适定的, 因此通常需要利用正则化方法克服其不适定性或恢复解的稳定性. 2021 年, 文献 [20] 使用迭代方法研究了反问题 (1.3) 特殊情况, 其中 (1.3) 式的主方程表示为:
众知, 经典 Tikhonov 方法由于其简单易算已被广泛应用于许多反问题的求解中, 并且可以获得良好的正则化效果. 然而, 其需要解的超光滑性. 因此, 近年来学者们引入分数 Tikhonov 正则化方法来处理相关反问题, 分数 Tikhonov 正则化方法可在数值上克服反问题解的超光滑性限制. 特别是当反问题的解是非光滑函数时, 具有较为满意的模拟效果. 此外注意到, 在理论方面, 当此类方法被用于处理反问题 (1.3) 时, 文中导出Hölder型的先验和后验收敛性结果. 关于运用此类方法研究反问题的文献, 请见文献 [21⇓⇓-24] 等. 本文首先建立反问题 (1.3) 的 Hölder 型条件稳定性结果. 然后, 基于不适定性分析, 构造分数Tikhonov正则化方法以恢复解对测量数据的连续依赖性. 同时, 在正则化参数的先验和后验选取规则下, 导出相应的 Hölder 型收敛性结果. 最后, 借助两个数值实验, 分别验证正则化方法对光滑和非光滑解的模拟效果.
2 预备知识
定义 2.1[25] 三参数 Mittag-Leffler 函数定义如下
其中,
引理 2.1[26] 对于
引理 2.2 基于引理 2.1, 设
其中,
引理 2.3 设
其中,
证 根据
证毕.
引理2.4 设
其中,
证 (1)
(2)
证毕.
引理 2.5 设
其中,
证 (1)
(2)
证毕.
3 反问题的不适定性和条件稳定性
定义空间
其中,
由文献 [16], 对于
设
定义
同理,
根据 (3.4) 式, 定义算子方程
其中,
显然,
定理 3.1 (3.7) 式中定义的算子
证 由 (3.7) 式, 我们定义有限秩算子
注意到, 当
定理 3.1 表明反问题 (1.3) 是不适定的, 即解不连续地依赖于测量数据. 然而, 如果精确解满足一定的先验条件, 就可建立反问题的条件稳定性. 下面, 在精确解的先验假设下, 我们建立反边值问题 (1.3) 的条件稳定性结果.
定理 3.2 设
则有稳定性结果
这里,
证 根据 (3.6) 式和 Hölder 不等式, 有
证毕.
4 分数 Tikhonov 正则化方法
在本节中, 基于文献 [27] 中的思想, 我们构造反问题 (1.3) 的分数 Tikhonov 正则化解. 正则化解被定义为如下泛函的极小元.
其中, 半范数
利用自伴紧算子
其中,
其中,
5 先验与后验选取规则下的收敛性估计
5.1 先验选取规则下的收敛性估计
在本小节中, 我们通过先验规则选取正则化参数, 给出并证明分数 Tikhonov 正则化方法的收敛性估计.
精确解和分数 Tikhonov 正则化解分别由 (3.6) 式和 (4.3) 式给出.
定理 5.1 假定先验条件 (3.9) 成立, 精确数据
(1) 当
(2) 当
其中,
证 由三角不等式, 得到
首先, 我们估计
接下来, 我们估计
结合不等式 (5.4) 和 (5.5), 可以得出
选取正则化参数
则由 (5.6) 式和 (5.7) 式, 可得收敛性结果
证毕.
5.2 后验选取规则下的收敛性估计
在本小节中, 我们考虑正则化参数
设
其中,
引理 5.1 设
(1)
(2)
(3)
(4) 对于
证 令
可完成此引理 5.1 的证明.
由引理 5.1, 知方程 (5.9) 有唯一解, 这说明了后验选取正则化参数的合理性. 为了获得收敛性估计结果, 我们需要以下引理.
引理 5.2 对固定的
证 根据后验选取规则 (5.9), 有
另一方面, 由引理 2.5, 可得
通过计算, 我们有
证毕.
定理 5.2 假定先验条件 (3.9) 成立, 精确数据
(1) 当
(2) 当
其中,
证 由三角不等式, 有
(1) 当
然后, 我们估计
由 (1.4)、(5.9) 及 (3.9) 式, 有
由 (5.17)、(5.18) 和 (5.19) 式, 可得
(2) 当
然后, 我们对
由 (1.4)、(5.9) 及 (3.9) 式, 可得
由 (5.17)、(5.20) 及 (5.21) 式, 我们有
证毕.
6 数值实验
本节通过一些数值实验验证分数 Tikhonov 正则化方法的模拟效果. 取
考虑正问题
对给定的函数
令
其中, 内积
测量误差界为
为了对数值结果进行灵敏度分析, 并通过以下公式计算相对均方根误差
在下面的例 6.1 和例 6.2 中, 我们取
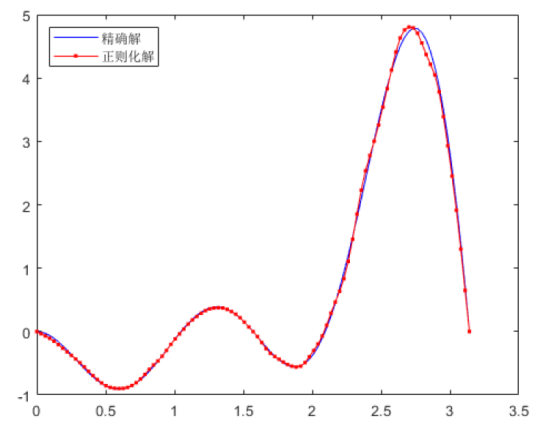
例 6.1 考虑反问题的解是光滑函数的情况, 选取
取
图1
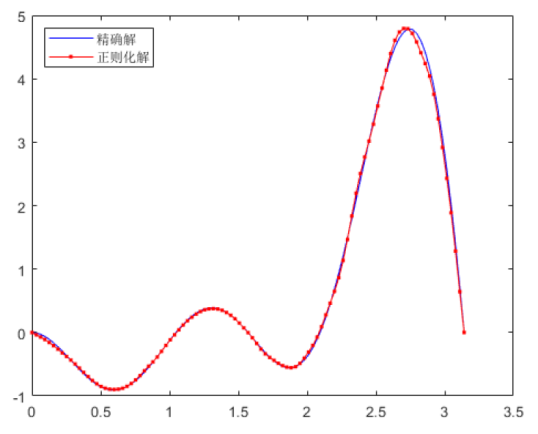
特别地, 当
图2
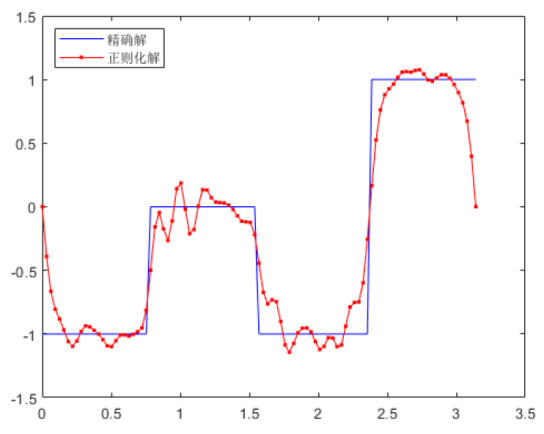
例 6.2 考虑反问题的解是分段函数的情形, 选取
取
图3
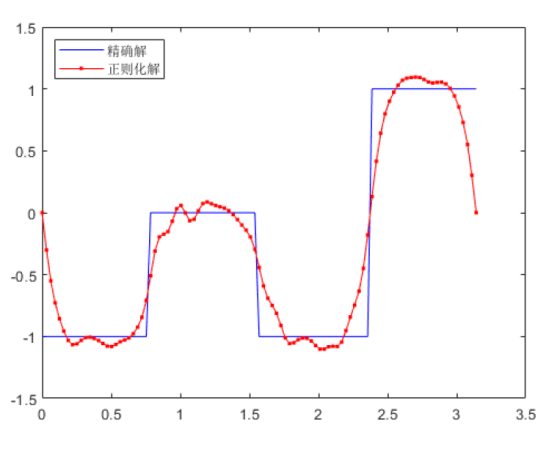
特别地, 当
图4
7 总结
文中考虑了一类 Tricomi-Gellerstedt-Keldysh 型分数阶椭圆方程的反边值问题. 首先建立了反问题的条件稳定性结果. 然后, 基于不适定性分析, 构造了分数 Tikhonov 正则化方法, 以恢复解对测量数据的连续依赖性. 同时, 在正则化参数的先验和后验选取规则下, 导出了相应的 Hölder 型收敛性结果. 数值结果表明, 该方法在求解所考虑的问题时是稳定可行的.
参考文献
Fundamental solutions for the Tricomi operator
Fundamental solutions for the Tricomi operator, II
Fundamental solutions of the Tricomi operator, III
On the solution of a nonlocal boundary value problem by the spectral method
The weighted
On mathematical and information technologies for modeling and control of regional development
A concave-convex elliptic problem involving the fractional Laplacian
Asymptotic analysis of the Dirichlet fractional Laplacian in domains becoming unbounded
An extension problem related to the fractional Laplacian
Dirichlet problem for the generalized Laplace equation with the Caputo derivative
A nonlocal fractional Helmholtz equation
Well-posedness of Tricomi-Gellerstedt-Keldysh-type fractional elliptic problems
Sulle equazioni lineari alle derivate parziali del secondo ordine di tipo ellittico sopra una superficie chiusa
On some cases of degenerate elliptic equations on the boundary of a domain
Iterative regularization method for an abstract ill-posed generalized elliptic equation
A fractional Tikhonov regularization method for identifying a space-dependent source in the time-fractional diffusion equation
On a final value problem for fractional reaction-diffusion equation with Riemann-Liouville fractional derivative
Solving the backward problem for space-fractional diffusion equation by a fractional Tikhonov regularization method
A fractional Tikhonov regularization method for an inverse backward and source problems in the time-space fractional diffusion equations
On solution of integral equation of Abel-Volterra type
Fractional extreme distributions
Iterated fractional Tikhonov regularization