分数阶椭圆方程反边值问题的分数 Tikhonov 正则化方法

数学物理学报 ›› 2024, Vol. 44 ›› Issue (4): 978-993.

分数阶椭圆方程反边值问题的分数 Tikhonov 正则化方法

张潇(),张宏武^*()

北方民族大学数学与信息科学学院银川 750021

收稿日期:2023-05-05 修回日期:2024-01-10 出版日期:2024-08-26 发布日期:2024-07-26
通讯作者: *张宏武, E-mail: zh-hongwu@163.com
作者简介:张潇, E-mail: 240324542@qq.com
基金资助:
宁夏自然科学基金(2022AAC03234);国家自然科学基金(11761004);宁夏高等教育一流学科建设基金(NXYLXK2017B09)

Fractional Tikhonov Regularization Method for an Inverse Boundary Value Problem of the Fractional Elliptic Equation

Zhang Xiao(),Zhang Hongwu^*()

School of Mathematics and Information Science, North Minzu University, Yinchuan 750021

Received:2023-05-05 Revised:2024-01-10 Online:2024-08-26 Published:2024-07-26
Supported by:
NSF of Ningxia(2022AAC03234);NSF of China(11761004);Construction Project of First-Class Disciplines in Ningxia Higher Education(NXYLXK2017B09)

摘要/Abstract

摘要：

该文研究了 Tricomi-Gellerstedt- Keldysh 型分数阶椭圆方程的反边值问题. 对于该不适定问题, 建立了条件稳定性结果. 基于问题的不适定性, 构造了分数 Tikhonov 正则化方法, 以恢复解对测量数据的连续依赖性. 在正则化参数的先验和后验选取规则下, 分别给出并证明了相应的 Hölder 型收敛性结果. 最后, 通过两个数值例子验证了分数 Tikhonov 正则化方法的模拟效果. 数值结果表明, 该方法能稳定有效地处理文中反问题.

关键词: 反边值问题, 分数阶椭圆方程, 分数 Tikhonov 正则化, 先验和后验收敛性估计, 数值模拟

Abstract:

In this paper, we study an inverse boundary value problem for fractional elliptic equation of Tricomi-Gellerstedt-Keldysh-type. For this ill-posed problem, a conditional stability result is established. Based on the ill-posedness analysis, a fractional Tikhonov regularization method was constructed to recover the continuous dependence of the solution on the measurement data. Under the a-priori and a-posteriori selection rules for regularization parameter, the corresponding convergence results of Hölder type are derived and proved, respectively. Finally, the simulation effectiveness of the fractional Tikhonov method is verified by two numerical examples. The numerical results show that the method works stably and effectively in dealing with the inverse problem in the text.

Key words: Inverse boundary value problem, Fractional elliptic equation, Fractional Tikhonov regularization, A-priori and a-posteriori convergence estimates, Numerical simulation

中图分类号:

O175

张潇, 张宏武. 分数阶椭圆方程反边值问题的分数 Tikhonov 正则化方法[J]. 数学物理学报, 2024, 44(4): 978-993.

Zhang Xiao, Zhang Hongwu. Fractional Tikhonov Regularization Method for an Inverse Boundary Value Problem of the Fractional Elliptic Equation[J]. Acta mathematica scientia,Series A, 2024, 44(4): 978-993.

图/表 10

图1

图2

表1

表2

表3

图3

图4

表4

表5

表6

参考文献 28

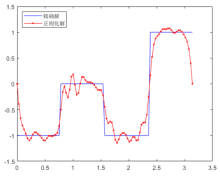
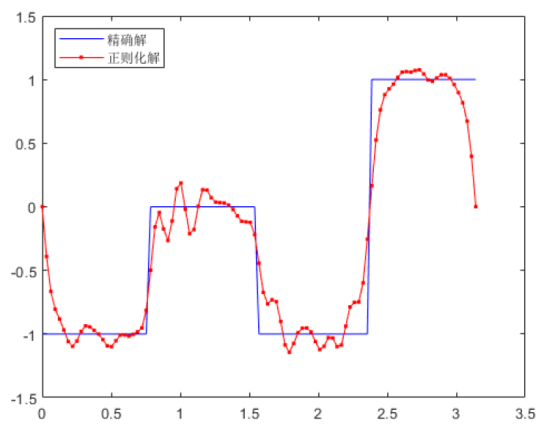
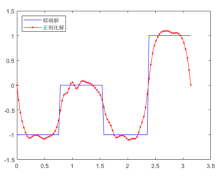
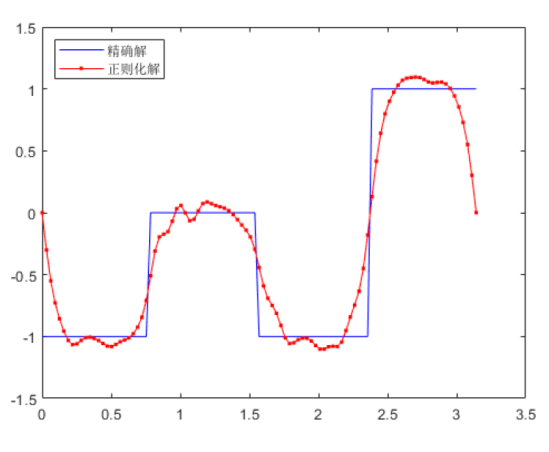
[1]	Algazin O D. Exact solution to the Dirichlet problem for degenerating on the boundary elliptic equation of Tricomi-Keldysh type in the half-space. 2016, arXiv:1603.05760
[2]	Neto J B, Gelfand I M. Fundamental solutions for the Tricomi operator. Duke Math J, 1999, 98(3): 465-483
[3]	Neto J B, Gelfand I M. Fundamental solutions for the Tricomi operator, II. Duke Math J, 2002, 111(3): 561-584
[4]	Neto J B, Gelfand I M. Fundamental solutions of the Tricomi operator, III. Duke Math J, 2005, 128(1): 119-140
[5]	Moiseev E I. On the solution of a nonlocal boundary value problem by the spectral method. Differ Equ, 1999, 35(8): 1094-1100
[6]	Xu N, Yin H. The weighted $ W^{2,p} $ estimate on the solution of the Gellerstedt equation in the upper half space. J Math Anal Appl, 2007, 332(2): 1148-1164
[7]	Bers L. Mathematical Aspects of Subsonic and Transonic Gas Dynamics. New York: Wiley, 1958
[8]	Otway T H. The Dirichlet Problem for Elliptic-Hyperbolic Equations of Keldysh Type. Berlin: Springer, 2012
[9]	Nakhushev A. On mathematical and information technologies for modeling and control of regional development. Dokl Adygsk (Cherkessk) Mezhdunar Akad Nauk, 2007, 9(1): 128-137
[10]	Brndle C, Colorado E, de Pablo A. A concave-convex elliptic problem involving the fractional Laplacian. Proc Roy Soc Edinburgh Sect A, 2013, 143(1): 39-71
[11]	Ambrosio V, Freddi L, Musina R. Asymptotic analysis of the Dirichlet fractional Laplacian in domains becoming unbounded. J Math Anal Appl, 2020, 485(2): 123845
[12]	Caffarelli L, Silvestre L. An extension problem related to the fractional Laplacian. Comm Partial Differential Equations, 2007, 32(8): 1245-1260
[13]	Masaeva O K. Dirichlet problem for the generalized Laplace equation with the Caputo derivative. Differ Equ, 2012, 48(3): 449-454
[14]	Kirane M, Turmetov B K, Torebek B T. A nonlocal fractional Helmholtz equation. Fract Differ Calc, 2017, 7(2): 225-234
[15]	Podlubny I. Fractional Differential Equations. San Diego: Academic Press, 1999
[16]	Ruzhansky M, Torebek B T, Turmetov B. Well-posedness of Tricomi-Gellerstedt-Keldysh-type fractional elliptic problems. J Integral Equations Appl, 2022, 34(3): 373-387
[17]	Cimmino G. Sulle equazioni lineari alle derivate parziali del secondo ordine di tipo ellittico sopra una superficie chiusa. Atti Accad Naz Lincei Rend Lincei Mat Appl, 1938, 7(1): 73-96
[18]	Gellerstedt S. Sur un probleme aux limites pour une equation linearire aux derivees partielles du second ordre de type mixtes. Uppsala: Uppsala University, 1935
[19]	Keldysh M. On some cases of degenerate elliptic equations on the boundary of a domain. Dokl Akad Nauk, 1951, 77: 181-183
[20]	Roumaissa S, Nadjib B, Faouzia R, et al. Iterative regularization method for an abstract ill-posed generalized elliptic equation. Asian-Eur J Math, 2021, 14(5): 2150069
[21]	Xiong X, Xue X. A fractional Tikhonov regularization method for identifying a space-dependent source in the time-fractional diffusion equation. Appl Math Comput, 2019, 349: 292-303
[22]	Tran N, Au V V, Zhou Y, et al. On a final value problem for fractional reaction-diffusion equation with Riemann-Liouville fractional derivative. Math Methods Appl Sci, 2020, 43(6): 3086-3098
[23]	Zheng G H, Zhang Q G. Solving the backward problem for space-fractional diffusion equation by a fractional Tikhonov regularization method. Math Comput Simulation, 2018, 148: 37-47
[24]	Djennadi S, Shawagfeh N, Arqub O A. A fractional Tikhonov regularization method for an inverse backward and source problems in the time-space fractional diffusion equations. Chaos Solitons Fractals, 2021, 150: 111127
[25]	Kilbas A A, Saigo M. On solution of integral equation of Abel-Volterra type. Differential Integral Equations, 1995, 8(5): 993-1011
[26]	Boudabsa L, Simon T, Vallois P. Fractional extreme distributions. Electron J Probab, 2020, 25: 1-20
[27]	Bianchi D, Buccini A, Donatelli M, et al. Iterated fractional Tikhonov regularization. Inverse Problems, 2015, 31(5): 055005
[28]	Morozov V A, Nashed Z, Aries A B. Methods for Solving Incorrectly Posed Problems. New York: Springer, 1984