2000 年, Aw、Rascle^[1]和 Zhang^[10]提出了一种二阶交通流模型

其中 $\rho(x, t) \geqslant 0$ 和 $v(x, t) \geqslant 0$ 分别为交通车辆的密度和速度, 变量 $w$ 表示相对速度, 标量 $\eta > 0$ 为微观中对应车辆加速与减速的加权. 压力项 $p(\rho)$ 为模拟实际交通反应的预测因子, 这里假设 $p(\rho)$ 满足

由文献[1]可知压力项前面的参数 $\eta$ 越小, 密度 $\rho$ 越大, 对应发生交通事故的概率越大. 有关 ARZ 模型的理论研究参见文献[4,7].

20 世纪 90 年代, 物理学家发现, 当高速公路上的车辆密度低于临界密度时, 交通流是稳定的 (称之为平滑流), 小干扰不会影响交通; 但一旦车辆密度超过临界值, 交通流量突然变得不稳定了 (称之为阻塞流), 小干扰的影响会呈指数级别增长. 例如, 交通早 (晚) 高峰期临近, 车辆密度逐渐升至临界值边缘, 平滑流与阻塞流之间突变 (即相变), 司机的粗心驾驶会造成更大范围的交通堵塞; 随着交通早 (晚) 高峰期结束, 阻塞流又恢复到平滑流 (相变也随即消失). 为了描述这一现象并预测交通事故, 2010 年 Herty 和 Schleper 等^[5]在 ARZ 交通流模型 (1.1) 的基础上, 改变压力项前面的参数 $\eta$, 将两个具有不同压力项系数的 ARZ 交通模型进行耦合, 提出以下耦合交通流 (CARZ) 模型

其中 $\rho^{}\geqslant 0$、 $v^{}\geqslant 0$ 和 $w^{\eta}, w^{\mu} \geqslant 0$ 分别表示密度、速度和对应路段上的相对速度, 压力项 $p(\rho)$ 满足 (1.2) 式. 考虑上述耦合 Aw-Rascle-Zhang 交通流模型黎曼问题, 给定初始状态

其中 $\rho_{\pm}, v_{\pm}$ 为已知常数. Herty 和 Schleper 等^[5]证明了黎曼问题 (1.3)-(1.4) 解的存在性, 但没有给出具体的显式解; 王文雷^[9]在其基础上进行了补充, 构造了大部分情况的黎曼显式解, 并证明了上述情况下的解的唯一性.

本文继续研究在单连通道路上具有不同压力项的耦合 Aw-Rascle-Zhang(CARZ) 交通流模型的黎曼问题 (1.3)-(1.4), 首先我们对文献[5,9]中缺失的情形 $v_- + \eta (\rho_-)^{\gamma} = v_+$ 进行了补充, 利用特征分析法和相变^[2,3]的相关理论, 构造出对应的显式解, 从而完善了 CARZ 模型的黎曼解, 为更好的模拟预测一些实际交通状况给予了理论支持. 其次, 令 CARZ 模型 (1.3) 中的压力项参数 $\mu \to \eta$, 得到对应的极限, 发现 Herty 和 Schleper 在 $v_- + \eta (\rho_-)^{\gamma}< v_+$ 这一情况下构造的黎曼解是不稳定的, 因此我们修正了该情况下的解, 并最终证明了黎曼解的唯一性和稳定性.

模型 (1.1) 的特征值为

故该模型是严格双曲的, 其对应的右特征向量为

当 $\rho \neq 0$, 有 $\nabla \lambda_1 \cdot \vec{r_1} \neq 0$, $\nabla \lambda_2 \cdot \vec{r_2} = 0$, 说明 $\lambda_1$ 是真正非线性的, $\lambda_2$ 是线性退化的; 当 $\rho=0$ 时, $\nabla \lambda_1 \cdot \vec{r}_1 = \nabla \lambda_2 \cdot \vec{r}_1 = 0$, 模型 (1.1) 是线性退化的, 其中 $\nabla$ 为向量 $(\rho, v)$ 的梯度. 第 1-Riemann 不变量 $w$ 和第 2-Riemann 不变量 $z$ 分别为

对于给定的左状态 $(\rho_-, v_-)$, 由 1-疏散波 $R_1$ 或 1-激波 $S_1$ 连接到右状态 $(\rho_+, v_+)$ 需满足如下条件

对应的 2-接触间断波 $J_2$

ARZ交通模型黎曼问题 (1.1)、(1.4) 的解详见文献[2], 下面只给出 $v_- + \eta (\rho_-)^{\gamma} < v_+$ 时的黎曼解. 如图1 所示, 解由疏散波 $R_1$ 和接触间断波 $J_2$ 组成, 真空波介于其中, 具体可表示如下

其中疏散波 $R_1$ 满足 (2.4) 式, 接触间断波 $J_2$ 的速度 $\tau = v_+$.

本节我们对文献[5,9]中讨论的情况进行补充, 考虑缺失情形 $v_- + \eta (\rho_-)^{\gamma} = v_+$ 下的黎曼解, 进一步完善耦合 ARZ 模型 (1.2)-(1.4) 的黎曼解. 本节假设 $\mu <\eta$, 即对应实际司机从有意识阶段突然转变为无意识阶段的情形. $\mu>\eta$ 的情况, 可类似讨论.

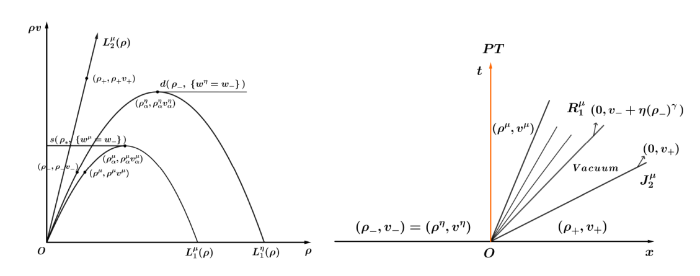
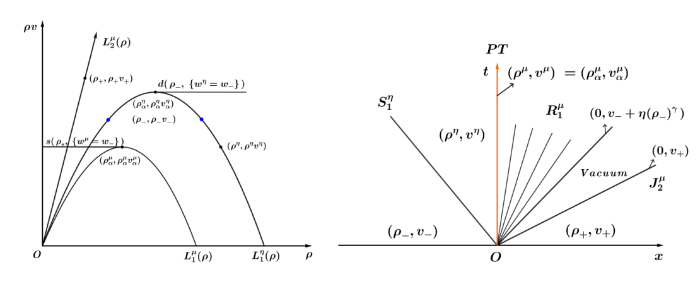
首先我们研究耦合 ARZ 模型 (1.3)-(1.4) 特征曲线的一些数学性质. 如图2 所示, 在 $M:=(\rho, \rho v)$ 平面上分别定义曲线 $L_1^{\eta} (\rho)$、 $L_1^{\mu} (\rho)$ 和 $L_2^{\mu} (\rho)$ 如下

记 $(\rho_{\alpha}^{\eta}, v_{\alpha}^{\eta} )$ 和 $(\rho_{\alpha}^{\mu}, v_{\alpha}^{\mu} )$ 分别为曲线 $L_1^{\eta}(\rho)$ 和 $L_1^{\mu}(\rho)$ 在 $M:=(\rho, \rho v)$ 平面顶点处对应的状态, $(\rho_*^{}, v_*^{} )$ 为曲线 $L_1^{\mu}(\rho)$ 和 $L_2^{\mu}(\rho)$ 相交时的状态, 经过简单的计算得到

性质 3.1 第 1-特征曲线 $L_1^{\eta}(\rho)$ 上的状态 $(\rho, v)$, 其特征速度满足以下关系

(1) 若 $\rho < \rho_{\alpha}^{\eta}$, 则有 $0= \lambda_1^{\eta}(\rho_{\alpha}^{\eta}, v_{\alpha}^{\eta}) < \lambda_1^{\eta}(\rho, v)$, 即对应特征波的波速为正;

(2) 若 $\rho \geqslant \rho_{\alpha}^{\eta}$, 则有 $\lambda_1^{\eta}(\rho, v) \leqslant \lambda_1^{\eta}(\rho_{\alpha}^{\eta}, v_{\alpha}^{\eta}) = 0$, 即对应特征波的波速非正.

第 1-特征曲线 $L_1^{\mu}(\rho)$ 上的状态 $(\rho, v)$, 也有上述类似的性质. 现考虑缺失情形 $v_- + \eta (\rho_-)^{\gamma} = v_+$ 下的黎曼问题 (1.3)-(1.4) 的解, 其它情形可参见文献[5,9]. 首先引入供给函数和需求函数的概念^[8], 如图2 所示, 供给函数为 $L_1^{\mu} (\rho)$ 曲线在 $(\rho, \rho v)$ 平面上的非增延拓部分, 记为 $s(\rho^{}_{};\{w^{\mu} = w_- \})$; 需求函数为 $L_1^{\eta} (\rho)$ 曲线在 $(\rho, \rho v)$ 平面上的非减延拓部分, 记为 $d(\rho, \{ w^{\eta} = w_- \} )$. 为获得 CARZ 模型 (1.3)-(1.4) 的唯一解, 相变 PT^[2,3] (即 $x=0$ 处) 需满足如下耦合条件^[5]

其中 $(\rho^{\eta}, v^{\eta})$ 和 $(\rho^{\mu}, v^{\mu})$ 为相变左右两侧的状态. 耦合条件 (3.1) 分别表示相变两侧流量守恒, 第二动量守恒, 以及交汇处允许通过的最大实际车流量. 如图2 和图3 所示, 第 1-特征曲线 $L_1^{\mu}(\rho)$ 与第 2-特征曲线 $L_2^{\mu}(\rho)$ 只在原点处相交, 即 $\rho_*=0$ (对应真空状态). 由于 $\mu < \eta$, 则有

此时交汇处的最大流量为

$d( \rho_-, \{ w^{\eta} = w_- \} )$ 的值取决于 $\rho_-$ 和 $\rho_{\alpha}^{\eta}$ 的值的大小关系, 下分 $\rho_- \geqslant \rho_{\alpha}^{\eta}$ 和 $\rho_- < \rho_{\alpha}^{\eta}$ 两种情况讨论.

情形 1$\rho_- \geqslant \rho_{\alpha}^{\eta}$

定理 3.1 令 $\mu < \eta$ 且 $v_+ = v_- + \eta(\rho_-)^{\gamma}$. 当 $\rho_- \geqslant \rho_{\alpha}^{\eta}$ 时, 黎曼问题 (1.3)-(1.4) 的解的结构可表示成

其中状态 $(\rho^{\mu}, v^{\mu})$ 满足

且 $\rho^{\mu} < \rho_{\alpha}^{\eta} <\rho_{\alpha}^{\mu}$; 疏散波 $R_1^{\eta}$、 $R_1^{\mu}$ 和接触间断波 $J_2^{\mu}$

“+”意味着“随后”.

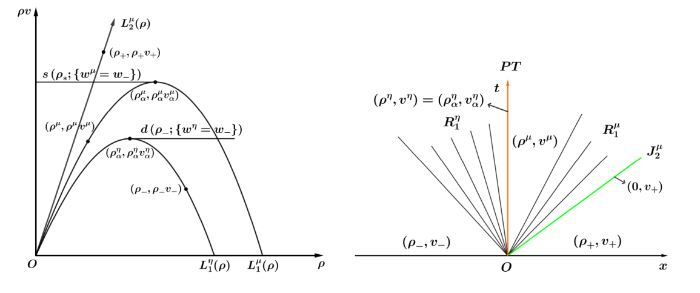
证 如图2 所示, 由耦合条件 (3.1) 可得

在 $\eta$-路段上, 由上式和 $\rho_- \geqslant \rho_{\alpha}^{\eta}$, 状态 $(\rho^{\eta}, v^{\eta})$ 是唯一确定的且与状态 $(\rho^{\eta}_{\alpha}, v^{\eta}_{\alpha})$ 重合, 即 $(\rho^{\eta}, v^{\eta}) = (\rho_{\alpha}^{\eta}, v_{\alpha}^{\eta})$. 根据 (2.4) 式, 左状态 $(\rho_-, v_-)$ 需通过 1-疏散波 $R_1^{\eta}$ 与右状态 $(\rho^{\eta}_{\alpha}, v^{\eta}_{\alpha})$ 连接. 疏散波 $R_1^{\eta}$ 左边界波速 $\lambda_1^{\eta}(\rho_-, v_-)$ 和右边界波速 $\lambda_1^{\eta}(\rho^{\eta}_{\alpha}, v^{\eta}_{\alpha})$ 满足

在 $\mu$-路段上, 由耦合条件 (3.1), 状态 $(\rho^{\mu}, v^{\mu})$ 满足

此时状态 $(\rho^{\mu}, v^{\mu})$ 有两种情况: $\rho^{\mu} < \rho^{\mu}_{\alpha}$ 和 $\rho^{\mu} > \rho^{\mu}_{\alpha}$. 由于 $\rho_* = 0 < \rho^{\mu}$, 左状态 $(\rho^{\mu}, v^{\mu})$ 需通过 1-疏散波 $R_1^{\mu}$ 与真空状态连接. 如果 $\rho^{\mu} > \rho^{\mu}_{\alpha}$, 由性质 3.1, 此时疏散波 $R_1^{\mu}$ 左边界波速$\lambda_1^{\mu}(\rho^{\mu}, v^{\mu}) < 0$, 即波速会出现负值, 根据文献[6]知矛盾! 如果 $\rho^{\mu} < \rho^{\mu}_{\alpha}$, 疏散波 $R_1^{\mu}$ 左边界波速 $\lambda_1^{\mu}(\rho^{\mu}, v^{\mu})$ 和右边界波速 $\lambda_1^{\mu}(0, v_- + \eta (\rho_-)^{\gamma})$ 满足

疏散波的波速为正, 故 $\rho^{\mu} < \rho^{\mu}_{\alpha}$.

由方程组 (3.5) 得 $\rho^{\mu} ( \, v^{\eta}_{\alpha} + \eta ( \rho^{\eta}_{\alpha})^{\gamma} - \mu (\rho^{\mu})^{\gamma} \, ) = \, \rho^{\eta}_{\alpha} v^{\eta}_{\alpha}$.定义函数 $F(\rho) = \rho^{} ( \, v^{\eta}_{\alpha} + \eta ( \rho^{\eta}_{\alpha})^{\gamma} - \mu \rho^{\gamma} \, ) - \rho^{\eta}_{\alpha} v^{\eta}_{\alpha}$. 由于 $\mu < \eta$, $F(0) \, = \, - \rho^{\eta}_{\alpha} v^{\eta}_{\alpha} < 0$ 且 $F(\rho_{\alpha}^{\eta}) \, = \, \eta ( \rho^{\eta}_{\alpha})^{\gamma} - \mu ( \rho^{\eta}_{\alpha})^{\gamma} > 0$, 根据零点定理, 存在 $\rho^{\mu} \in (0, \rho^{\eta}_{\alpha})$, 使得 $F(\rho^{\mu}) = 0$; 其次, 对 $\forall \rho \in (0, \rho_{\alpha}^{\mu})$ 有 $F'(\rho) = v^{\eta}_{\alpha} + \eta ( \rho^{\eta}_{\alpha})^{\gamma} - \mu (1+\gamma) \rho^{\gamma} > 0$, 函数 $F(\rho)$ 在区间 $[\rho_{\alpha}^{\mu}]$ 上严格单调递增, 则存在唯一的 $\rho^{\mu} \in [\rho^{\mu}_{\alpha}]$, 使得 $F(\rho^{\mu}) = 0$ 且 $0< \rho^{\mu} < \rho_{\alpha}^{\eta}$, 故由方程组 (3.5) 可以唯一确定状态 $(\rho^{\mu}, v^{\mu})$.

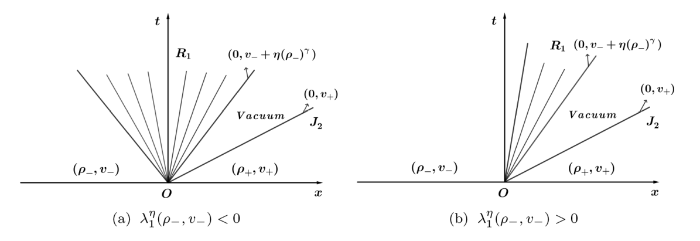
如图2 所示, 真空状态通过接触间断波 $J_2^{\mu}$ 与右状态 $(\rho_+, v_+)$ 连接, 其波速 $\tau$ 满足

特别地, 根据已知条件 $v_- + \eta(\rho_-)^{\gamma} = v_+$, 则 $\lambda_1^{\mu}(0, v_- + \eta (\rho_-)^{\gamma}) = \tau^{} = v_+$, 即疏散波 $R_1^{\mu}$ 的右界与接触间断波 $J_2^{\mu}$ 重合.

情形 2$\rho_- < \rho_{\alpha}^{\eta}$

定理 3.2 令 $\mu < \eta$ 且 $v_+ = v_- + \eta(\rho_-)^\gamma$. 当 $\rho_- < \rho_{\alpha}^{\eta}$ 时, 黎曼问题 (1.3)-(1.4) 的解的结构可表示成

其中状态 $(\rho^{\mu}, v^{\mu})$ 满足

$\rho^{\mu}< \rho_{-} < \rho_{\alpha}^{\mu}$; 疏散波 $R_1^{\mu}$ 和 接触间断波 $J_2^{\mu}$

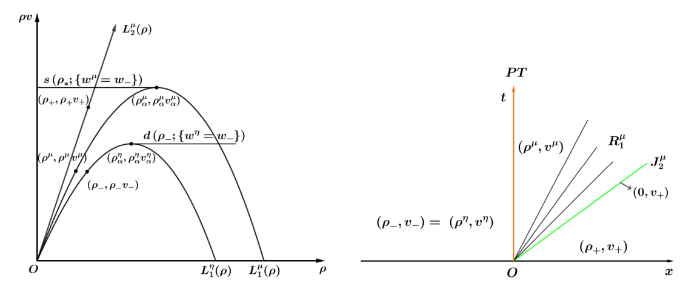
证 如图3 所示, 由耦合条件 (3.1) 可得

在 $\eta$-路段上, 由上式和 $\rho_- < \rho_{\alpha}^{\eta}$, 状态 $( \rho^{\eta}, v^{\eta})$ 是唯一确定的且与状态 $(\rho_-, v_-)$ 重合, 即 $(\rho^{\eta}, v^{\eta}) = (\rho_-, v_-)$, 该路段上状态唯一.

在 $\mu$-路段上, 类似定理 3.1 证明, 有 $\rho^{\mu} <\rho^{\mu}_{\alpha}$. 由耦合条件 (3.1), 状态 $(\rho^{\mu}, v^{\mu})$ 满足 (3.7) 式, 从而 $\rho^{\mu} ( \, v^{}_{-} + \eta ( \rho^{}_{-})^{\gamma} - \mu (\rho^{\mu})^{\gamma} \, ) = \rho_- v_-$. 定义函数 $G(\rho) = \rho^{} ( \, v_{-} + \eta ( \rho^{}_{-})^{\gamma} - \mu \rho^{\gamma} \, ) - \rho_- v_-$. 由于 $\mu < \eta$, $G(0) \, = \, - \rho^{}_{-} v^{}_{-} < 0$ 且 $G(\rho_-) = \eta (\rho_-)^{\gamma} - \mu (\rho_-)^{\gamma} > 0$, 根据零点定理, 存在 $\rho^{\mu} \in (0, \rho^{}_{-})$, 使得 $G(\rho^{\mu}) = 0$; 其次, 对 $\forall \rho \in (0, \rho^{\mu}_{\alpha})$ 有 $G'(\rho) = v^{}_{-} + \eta ( \rho^{}_{-})^{\gamma} - \mu ( 1 + \gamma ) \rho^{\gamma} \, > 0$, 函数 $G(\rho)$ 在区间 $[\rho^{\mu}_{\alpha}]$ 上严格单调递增, 则存在唯一的 $\rho^{\mu} \in [\rho^{\mu}_{\alpha}]$, 使得 $G(\rho^{\mu}) = 0$ 且 $0 < \rho^{\mu} < \rho_-$, 故由方程组 (3.7) 可以唯一确定状态 $(\rho^{\mu}, v^{\mu})$.

由于 $\rho_* = 0 < \rho^{\mu}$, 左状态 $(\rho^{\mu}, v^{\mu})$ 需先通过 1-疏散波 $R_1^{\mu}$ 与真空状态连接, 疏散波 $R_1^{\mu}$ 左边界波速 $\lambda_1^{\mu}(\rho^{\mu}, v^{\mu})$ 和右边界波速 $\lambda_1^{\mu}(0, v_- + \eta (\rho_-)^{\gamma})$ 满足

疏散波的波速为正. 如图3 所示, 真空状态通过接触间断波 $J_2^{\mu}$ 与右状态 $(\rho_+, v_+)$ 连接, 其波速 $\tau$ 满足

特别地, 根据已知条件 $v_- + \eta(\rho_-)^{\gamma} = v_+$, 则 $\lambda_1^{\mu}(0, v_- + \eta (\rho_-)^{\gamma}) = \tau^{} = v_+$, 即疏散波 $R_1^{\mu}$ 的右界与接触间断波 $J_2^{\mu}$ 重合.

本节研究黎曼问题 (1.3)-(1.4) 当压力项参数 $\mu \to \eta$ 时解的极限性态. 不失一般性, 本节假设 $\mu > \eta$, $\mu < \eta$ 的情况可类似讨论. 进一步, 根据解的唯一性和稳定性, 我们修正并补充了文献[5]中上述黎曼问题在情形 $v_- + \eta(\rho_-)^{\gamma} \leqslant v_+$ 的解, 并证明了 CARZ 模型的黎曼解的适定性.

当 $\mu \to \eta$ 时, 可以证明除 $v_- + \eta (\rho_-)^{\gamma} < v_+$ 情形, 文献[5,9]中的黎曼解(即问题 (1.3)-(1.4) 的解) 均收敛到问题 (1.1)、(1.4) 的解. 因此, 本节只考虑情形 $v_- + \eta (\rho_-)^{\gamma} \leqslant v_+$ 下黎曼解的渐近性态. 在该情形下且 $\eta$ 充分小时, 文献[5]中黎曼问题 (1.3)-(1.4) 的解的结构如下

(1) 当 $\rho_- v_- > \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$ 时

其中状态 $(\rho^{\eta}, v^{\eta})$ 满足

激波 $S_1^{\eta}$, 疏散波 $R_1^{\mu}$ 和接触间断波 $J_2^{\mu}$

(2) 当 $\rho_- v_- < \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$ 时

其中状态 $(\rho^{\mu}, v^{\mu})$ 满足 (3.7) 式, 激波 $S_1^{\mu}$ 和 接触间断波 $J_2^{\mu}$

注 4.1 当 $v_- + \eta (\rho_-)^{\gamma} < v_+$ 且 $\rho_- v_- < \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$ 时, 由 (3.7) 式可得

根据极限的四则运算法知极限 $\lim\limits_{\mu \to \eta } v^{\mu}$ 存在, 说明解 (4.4) 当 $\mu \to \eta$ 时的极限仍含有激波, 与解 (2.6) 不一致. 故文献[5]中在情形 $v_- + \eta (\rho_-)^{\gamma} < v_+$ 且 $\rho_- v_- < \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$ 下的解不适定.

我们重新构造黎曼问题 (1.3)-(1.4) 在情形 $v_- + \eta(\rho_-) < v_+$ (此时 $\eta$ 不需要充分小) 下的解并讨论解的稳定性. 类似定理 3.1 和定理 3.2 的讨论, 我们可以得到如下定理.

定理 4.1 令 $\mu > \eta$ 且 $v_- + \eta (\rho_-)^{\gamma} < v_+,$

(1) 如果 $\rho_- v_- < \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$ 且 $\rho_- \geqslant \rho_{\alpha}^{\eta}$, 则黎曼问题 (1.3)-(1.4) 的解的结构可表示成 (如图4)

其中状态 $(\rho^{\eta}_{}, v^{\eta}_{})$ 由方程组 (4.2) 确定且 $\rho^{\eta} > \rho_{\alpha}^{\eta}$, 疏散波 $R_1^{\eta}$、 $R_1^{\mu}$ 和接触间断波 $J_2^{\mu}$

(2) 如果 $\rho_- v_- < \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$ 且 $\rho_- < \rho_{\alpha}^{\eta}$, 则黎曼问题 (1.3)-(1.4) 的解的结构可表示成 (如图5)

其中状态 $(\rho^{\mu}, v^{\mu})$ 满足 $\rho^{\mu} < \rho^{\mu}_{\alpha}$ 和 (3.7) 式, 疏散波 $R_1^{\mu}$ 和接触间断波 $J_2^{\mu}$

(3) 如果 $\rho_- v_- > \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$, 则黎曼问题 (1.3)-(1.4) 的解的结构为 (4.1) 式 (如图6).

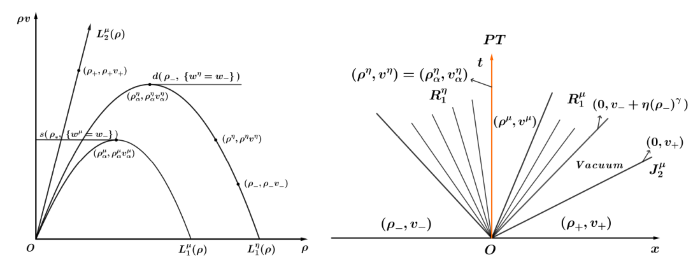
证 (1) 如图4 所示, 由于 $\rho_- v_- < \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$且 $\rho_- \geqslant \rho_{\alpha}^{\eta}$, 则有

根据耦合条件 (3.1) 可得, 相变左侧状态 $(\rho^{\eta}, v^{\eta})$ 由式 (4.2) 确定, 右侧状态 $(\rho^{\mu}, v^{\mu})= (\rho^{\mu}_{\alpha}, v^{\mu}_{\alpha})$.

在 $\eta$- 路段上, 状态 $(\rho^{\eta}, v^{\eta})$ 有两种情况: $\rho^{\eta} < \rho^{\eta}_{\alpha} < \rho_-$ 和 $\rho^{\eta}_{\alpha} < \rho^{\eta} < \rho_-$. 根据 (2.4) 式, 左状态 $(\rho_-, v_-)$ 需通过 1-疏散波 $R_1^{\eta}$ 与右状态 $(\rho^{\eta}_{}, v^{\eta}_{})$ 连接. 若 $\rho^{\eta} < \rho^{\eta}_{\alpha} < \rho_-$, 由性质 3.1, 疏散波 $R_1^{\eta}$ 右边界波速 $\lambda_1^{\eta}(\rho^{\eta}, v^{\eta}) > 0$, 即波速会出现正值, 矛盾! 若 $\rho^{\eta}_{\alpha} < \rho^{\eta} < \rho_-$, 疏散波 $R_1^{\eta}$ 左边界波速 $\lambda_1^{\eta}(\rho_{-}, v_{-})$ 和右边界波速 $\lambda_1^{\eta}(\rho^{\eta}, v^{\eta} )$ 满足

疏散波的波速为负, 故 $\rho^{\eta}_{\alpha} < \rho^{\eta}$. 类似定理 3.1 中的证明可得: 由方程组 (4.2) 可以唯一确定状态 $(\rho^{\eta}, v^{\eta})$. 在 $\mu$-路段上, 左状态 $(\rho^{\mu}, v^{\mu})= (\rho^{\mu}_{\alpha}, v^{\mu}_{\alpha})$ 需通过 1- 疏散波 $R_1^{\mu}$ 与真空状态连接, 疏散波 $R_1^{\mu}$ 左边界波速 $\lambda_1^{\mu}(\rho^{\mu}_{\alpha}, v^{\mu}_{\alpha})$ 和右边界波速 $\lambda_1^{\mu}(0, v_- + \eta (\rho_-)^{\gamma})$ 满足

疏散波的波速非负. 最后, 真空状态通过接触间断波 $J_2^{\mu}: \tau^{} = v_+$ 与右状态 $(\rho_+, v_+)$ 连接.

(2) 如图5 所示, 由于 $\rho_- v_- < \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$ 且 $\rho_- < \rho_{\alpha}^{\eta}$, 则有

由耦合条件 (3.1) 可得, 相变左侧状态 $(\rho^{\eta}, v^{\eta}) = (\rho_-, v_-)$, 右侧状态 $(\rho^{\mu}, v^{\mu})$ 由 (3.7) 式确定. 类似定理 4.1(1) 部分证明可得 $\rho^{\mu} < \rho^{\mu}_{\alpha}$ 且 $(\rho^{\mu}, v^{\mu})$ 唯一. 在 $\mu$- 路段上, 状态 $(\rho^{\mu}, v^{\mu})$ 与 $(\rho_+, v_+)$ 的连接与定理 4.1(1) 完全相同, 证明省略.

(3) 如图6 所示, 由于 $\rho_- v_- > \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$, 则有

由耦合条件 (3.1) 可得, 相变左侧状态 $(\rho^{\eta}, v^{\eta})$ 由式 (4.2) 确定, 右侧状态 $(\rho^{\mu}, v^{\mu})= (\rho^{\mu}_{\alpha}, v^{\mu}_{\alpha})$. 在 $\eta$-路段上, 状态 $(\rho_{-}, v_{-})$ 需通过 1-激波 $S_1^{\eta}$ 与右状态 $(\rho^{\eta}, v^{\eta})$ 连接, 在 $\mu$-路段上, 状态 $(\rho^{\eta}, v^{\eta})$ 与 $(\rho_+, v_+)$ 的连接与定理 4.1(1) 完全相同, 证明省略. 证毕.

注 4.2 当 $v_- + \eta(\rho_-)^{\gamma} = v_+$ 时, 则有 $\lambda_1^{\mu}(0, v_- + \eta (\rho_-)^{\gamma}) = \tau^{} = v_+$, 即解 (4.7)、(4.10) 和 (4.1) 的疏散波 $R_1^{\mu}$ 的右边界与接触间断波 $J_2^{\mu}$ 重合.

定理 4.2 令 $v_- + \eta (\rho_-)^{\gamma} < v_+$. 当 $\mu \to \eta$ 时, CARZ 模型的黎曼解 (4.7)、(4.10) 和 (4.1) 都收敛到ARZ模型的黎曼解 (2.6).

证 令 $\mu \to \eta$, 第 1-特征曲线 $L_1^{\mu}(\rho)$ 有

即曲线 $L_1^{\mu}(\rho)$ 和 $L_1^{\eta}(\rho)$ 将会重合, 对应最高点状态$(\rho_{\alpha}^{\mu}, v_{\alpha}^{\mu})$ 与 $(\rho_{\alpha}^{\eta}, v_{\alpha}^{\eta})$ 也将会重合

(1) 当 $\rho_- v_- < \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$ 且 $\rho_- \geqslant \rho_{\alpha}^{\eta}$ 时, 由定理 4.1(1) 知: 黎曼问题 (1.3)、(1.4) 的解的结构为 (4.7). 考虑第 1-特征曲线 $L_1^{\eta}(\rho)$ 函数 $m_1^{\eta}$, 经过简单的计算可得

故其一阶导数是严格单调递减的, 令 $\frac{{\rm d} m_1^{\eta}}{{\rm d} \rho} = 0$, 得到唯一驻点 $\rho_{\alpha}^{\eta}$, 函数 $m^{\eta}_1$ 在 $[\rho^{\eta}_{\alpha}]$ 区间上严格单调递增, 在 $(\rho^{\eta}_{\alpha}, +\infty)$ 上严格单调递减, 即 $(\rho^{\eta}_{\alpha}, \rho^{\eta}_{\alpha}v^{\eta}_{\alpha})$ 是曲线 $L_1^{\eta}(\rho)$ 在 $M:=(\rho, \rho v)$ 平面上的唯一最大值点.

对方程组 (4.2) 的第一式两边分别令 $\mu \to \eta$ 得

因此, 当 $\mu \to \eta$ 时, $(\rho^{\eta}, v^{\eta}) = (\rho_{\alpha}^{\eta}, v_{\alpha}^{\eta})$. 根据上式、(4.8) 和 (4.9)式, 疏散波 $R_1^{\eta}$ 右边界波速和 $R_1^{\mu}$ 左边界波速

此时疏散波 $R_1^{\eta}$ 右边界、 $R_1^{\mu}$ 左边界与 $t$ 轴三者重合. 因此解 (4.7) 中 $R_1^{\eta}$ 和 $R_1^{\mu}$ 将会连接起来, 同时相变 PT 将会消失. 疏散波 $R_1^{\mu}$ 右边界波速和接触间断波 $J^{\mu}_2$ 的波速当 $\mu \to \eta$ 时均保持不变. 综上, 当 $\mu \to \eta$ 时, 黎曼解 (4.7) 收敛到 ARZ 模型的黎曼解 (2.6), 如图1(a) 所示.

(2) 当 $\rho_- v_- < \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$ 且 $\rho_- < \rho_{\alpha}^{\eta}$ 时, 由定理 4.1(2) 知: 黎曼问题 (1.3)-(1.4) 的解的结构为 (4.10) 式. 根据 (3.7) 式中的第一个等式得 $v^{\mu} = \frac{\rho_- v_-}{\rho^{\mu}}$, 将其带入 (3.7) 式的第二个等式有 $\frac{\rho_- v_-}{\rho^{\mu}} + \mu (\rho^{\mu})^{\gamma} = v_- + \eta (\rho_-)^{\gamma}$. 对上式两边关于 $\mu$ 求导有

由定理 4.1(2) 知 $\rho^{\mu} < \rho^{\mu}_{\alpha}$, 从而当 $\rho \in (0, \rho_{\alpha}^{\mu})$ 时, 有 $\frac{{\rm d} \rho^{\mu}}{{\rm d} \mu } >0$. 对方程组 (3.7) 两边分别令 $\mu \to \eta$ 得

结合 (4.17) 式和 $\frac{{\rm d} \rho^{\mu}}{{\rm d} \mu } >0$, 可以得到 $\lim\limits_{\mu \to \eta } \rho^{\mu} = \rho_-$ 和 $\lim\limits_{\mu \to \eta } v^{\mu} = v_-$. 根据 (4.11) 式, 疏散波 $R_1^{\mu}$ 左边界波速

疏散波 $R_1^{\mu}$ 右边界波速和接触间断波 $J^{\mu}_2$ 的波速

综上, 当 $\mu \to \eta$ 时, 黎曼解 (4.10) 的收敛到 ARZ 模型的黎曼解 (2.6), 如图1(b)所示.

(3) 当 $\rho_- v_- > \rho_{\alpha}^{\mu} v_{\alpha}^{\mu}$ 时, 根据极限的保号性有 $\rho_- v_- \geqslant \lim\limits_{\mu \to \eta } \rho^{\mu}_{\alpha} v^{\mu}_{\alpha} = \rho_{\alpha}^{\eta} v_{\alpha}^{\eta}$, 另一方面由状态 $(\rho_{\alpha}^{\eta}, v_{\alpha}^{\eta})$ 的定义有 $\rho_- v_- \leqslant \rho_{\alpha}^{\eta} v_{\alpha}^{\eta}$, 从而 $(\rho_-, v_-) =(\rho_{\alpha}^{\eta}, v_{\alpha}^{\eta})$. 此时 黎曼问题 (1.3)-(1.4)解的结构为 (4.1) 式且 $\rho^{\eta}> \rho^{\eta}_{\alpha}$. 对方程组 (4.2) 两边分别令 $\mu \to \eta$ 得

根据 (4.18) 式, 定义 $H(\rho)= \rho^{} ( \, v_{\alpha}^{\eta} + \eta ( \rho_{\alpha}^{\eta} )^{\gamma} - \eta \rho^{\gamma} \, ) - \rho_{\alpha}^{\eta} v_{\alpha}^{\eta}$, 其中 $\rho \in [\rho_{\alpha}^{\eta}, (\frac{ v_- + \eta (\rho_-)^{\gamma} }{ \eta } )^{\frac{1}{\gamma}}]$. 计算得 $H'(\rho) = \, v_{\alpha}^{\eta} + \eta ( \rho_{\alpha}^{\eta})^{\gamma} - \eta ( 1 + \gamma ) \rho^{\gamma} > 0$, 故 $H(\rho)$ 在区间 $[\rho_{\alpha}^{\eta}, (\frac{ v_- + \eta (\rho_-)^{\gamma} }{ \eta } )^{\frac{1}{\gamma}}]$ 上严格单调递增. 另一方面 $H(\rho^{\eta}_{\alpha})=0$, 故由方程组 (4.18) 可以得唯一解 $(\rho^{\eta}, v^{\eta}) = (\rho^{\eta}_{\alpha}, v^{\eta}_{\alpha})$. 因此当 $\mu$$\to$$\eta$ 时, $(\rho_-, v_-) = (\rho^{\eta}_{\alpha}, v^{\eta}_{\alpha}) = (\rho^{\eta}, v^{\eta})$, 即激波 $S_1^{\eta}$ 和相变 $PT$ 将会消失; 疏散波$R_1^{\mu}$ 左边界波速 $\lim\limits_{\mu \to \eta } \lambda_1^{\mu}(\rho_{\alpha}^{\mu}, v_{\alpha}^{\mu}) = v^{\eta}_{\alpha} - \eta \gamma (\rho^{\eta}_{\alpha} )^{\gamma} = 0$; 疏散波 $R_1^{\mu}$ 右边界波速和接触间断波 $J^{\mu}_2$ 的波速当 $\mu$$\to$$\eta$ 时均保持不变. 综上, 当 $\mu$$\to$$\eta$ 时, 黎曼解 (4.1) 收敛到 ARZ 模型的黎曼解 (2.6).

由以上讨论可知, 当压力项前面的参数 $\mu$$\to$$\eta$ 时, 黎曼问题 (1.3)-(1.4) 在情形 $v_- + \eta (\rho_-)^{\gamma} < v_+$ 下的黎曼解 (4.7)、(4.10) 和 (4.1) 的极限恰好与相同初值下的 ARZ 模型 (1.1) 的黎曼解的结构一致. 也就是说, 在上述情形下, 当压力趋于一致时, CARZ 模型 (1.3) 的解的收敛到 ARZ 模型 (1.1) 的解. 证毕.

当 $\mu \to \eta$ 时, 耦合 Aw-Rascle-Zhang 交通流模型的黎曼问题 (1.3)-(1.4) 在情形 $v_- + \eta (\rho_-)^{\gamma} = v_+$ 下的黎曼解的极限可类似定理 4.2 讨论, 我们得出如下定理.

定理 4.3 令 $v_- + \eta(\rho_-)^{\gamma} \leqslant v_+$, 耦合 ARZ 模型的黎曼问题 (1.3)-(1.4) 的解存在唯一且稳定; 当 $\mu \to \eta$ 时, 该黎曼解对应的收敛至 ARZ 模型 (1.1)、(1.4) 的解.