基于 Bernstein Copula 函数的随机变量序列的 Max-Sum 局部等价式

基于 Bernstein Copula 函数的随机变量序列的 Max-Sum 局部等价式

明瑞星^,¹, 楼振瀚^,¹, 崔盛^,²^,³^,^*, 龚婵^,²^,³

¹浙江工商大学统计与数学学院杭州 310018

²三峡大学理学院湖北宜昌 443002

³三峡数学研究中心湖北宜昌 443002

Local Max-sum Equivalence of Random Variables with Bernstein Copula

Ming Ruixing^,¹, Lou Zhenhan^,¹, Cui Sheng^,²^,³^,^*, Gong Chan^,²^,³

¹School of Statistics and Mathematics, Zhejiang Gongshang University, Hangzhou 310018

²Science College,China Three Gorges University, Hubei Yichang 443002

³Three Gorges Mathematical Research Center,China Three Gorges University, Hubei Yichang 443002

通讯作者: *崔盛, E-mail: cuisheng@ctgu.edu.cn

收稿日期: 2023-12-1 修回日期: 2024-04-29

基金资助:

浙江省重点建设高校优势特色学科 (浙江工商大学统计学)、浙江工商大学“数字+” 学科建设管理项目“数据资产: 经济理论, 价值核算, 市场交易与政策创新(SZJ2022B004)
浙江省统计科学研究基地项目高维情形下最小方差投资组合研究(22TJD02)
宜昌市大学科学研究与应用项目(A21-3-018)

Received: 2023-12-1 Revised: 2024-04-29

Fund supported:

Characteristic & Preponderant Discipline of Key Construction Universities in Zhejiang Province (Zhejiang Gongshang University–Statistics), the Collaborative Innovation Center of Statistical Data Engineering Technology & Application, Digital + Discipline Construction Project(SZJ2022B004)
Research on Minimum Variance Portfolio of Zhejiang Statistical Science Research Base Project in High dimension(22TJD02)
Scientific Research and Application Project of Universities in Yichang City(A21-3-018)

作者简介 About authors

明瑞星,E-mail:rxming@zjgsu.edu.cn;

楼振瀚,E-mail:lzh00214@163.com;

龚婵,E-mail:2556516736@qq.com

摘要

该文考虑一类具有局部长尾分布, 但不一定具有相同分布的随机变量序列, 其联合分布由 Bernstein copula 函数进行联系. 研究其部分和及其最大值的局部分布的渐近性质. 在假设诸随机变量服从局部次指数分布的条件下, 得到了 Max-Sum 局部等价性. 该等价性从局部和相依的角度描述了随机游动的一次大跳原理. 数值实验表明所得结果稳定可行.

关键词： Bernstein copula; Max-Sum 局部等价性; 局部次指数分布; 一次大跳原理

Abstract

In this paper, we consider a sequence of non-negative dependent and not necessarily identically distributed random variables with local long-tailed marginal distributions and Bernstein copula and study the local asymptotic behavior of the tail of their partial sum and maximum. Then, under a suitable condition for local subexponentiality, we obtain the local max-sum equivalence. The result indicates that the big-jump principle of random walks remains valid in its local version under more general dependency assumptions. The numerical experimental results under different parameter settings further validate the stability and feasibility of the obtained results.

Keywords： Bernstein copula; Local max-sum equivalence; Local subexponentiality; Principle of a single big jump

PDF (658KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

明瑞星, 楼振瀚, 崔盛, 龚婵. 基于 Bernstein Copula 函数的随机变量序列的 Max-Sum 局部等价式[J]. 数学物理学报, 2024, 44(4): 1110-1125

Ming Ruixing, Lou Zhenhan, Cui Sheng, Gong Chan. Local Max-sum Equivalence of Random Variables with Bernstein Copula[J]. Acta Mathematica Scientia, 2024, 44(4): 1110-1125

1 引言

设 $\{X_i, i \ge 1\}$ 为一非负随机变量序列, 其中 ${X_i}$ 的分布为 $F_i$ , $i\geq 1$ . 对 $n\geq 2$ , 记该随机变量序列的部分和为 $S_n=\sum\limits_{i=1}^{n}X_i$ , 最大值为 $X_{(n)}=\max\limits_{1\le i \le n}X_i$ , 并用 $F_{S_n}$ 表示 $S_{n}$ 的分布, 用 $F_{X_{(n)}}$ 表示 $X_{(n)}$ 的分布. 对某个固定的 $T\in (0, \infty]$ , 记 $\Delta_{T}=(0,T]$ ,

$\begin{eqnarray*} F_i(x+\Delta_{T})= F_i(x+T)-F_i(x). \end{eqnarray*}$

当 $0<T<\infty$ 时, 称 $F_i(x+\Delta_{T})$ 为 $F_i$ 的局部分布; 当 $T=\infty$ 时, $F_i(x+\Delta_{T})=1-F_i(x):=\overline{F}_i(x)$ , 称之为 $F_i$ 的尾分布. 全文约定, 对于任意两个非负函数 $a(x)$ 和 $b(x)$ , 记号 $a(x)=O(b(x))$ 表示 $\limsup\limits_{x\rightarrow\infty}\frac{a(x)}{b(x)}< \infty$ ; $a(x)=o(b(x))$ 表示 $\lim\limits_{x\rightarrow\infty}\frac{a(x)}{b(x)}=0$ ; $a(x)\sim b(x)$ 表示 $\lim\limits_{x\rightarrow\infty}\frac{a(x)}{b(x)}=1$ . 如果未对 $x$ 的极限行为做特殊说明, 那么本文中的所有极限关系都是在 $x\rightarrow\infty$ 情况下进行的.

研究 $S_n$ 和 $X_{(n)}$ 的局部分布和尾分布的渐近性质是应用概率论中重要的研究问题, 特别是寻求关系式

$\begin{align*} F_{S_n}(x+\Delta_{T})\sim F_{X_{(n)}}(x+\Delta_{T}) \end{align*}$

(1.1)

成立的条件成为许多学者关注的课题. 为以示区别, 当 $0<T<\infty$ 时, 称关系式 (1.1) 为 Max-Sum 局部等价式; 当 $T=\infty$ 时, 称关系式 (1.1) 为 Max-Sum 全局等价式. 在金融投资组合分析, 保险风险理论和排队理论等领域, 当随机变量相互独立且服从次指数分布时, 部分和的尾部渐近行为被形象地描述为“一次大跳”, 这意味着 Max-Sum 全局等价式成立.

Max-Sum 全局等价的概念由 Embrechts 和 Goldie^[1] 提出. 当 $\{X_i, i\geq1\}$ 独立同分布时, Max-Sum 全局等价式成立意味着共同分布 $F\in \mathcal{S}$ ( $\mathcal{S}$ 称为次指数分布族, 在下一节的定义 2.1 中, 当 $T=\infty$ 时, $\mathcal{S}_{\Delta(T)}$ 就是 $\mathcal{S}$ ). Geluk 和 Vries^[2] 给出了独立不同分布的随机变量序列 Max-Sum 全局等价式成立的一个充分条件

$\begin{align*} \mbox{对任意的}\ 1\le i,j\le n, F_i\ast F_j\in \mathcal S. \end{align*}$

(1.2)

但是, 在金融与保险领域中, 独立性假设一般并不成立. 学者们转而研究在怎样的相依性假设下, Max-Sum 全局等价仍然成立; 或者如果 Max-Sum 全局等价不成立, 部分和的渐近性质会呈现何种特征. 相关结果见文献 [3 ⇓⇓⇓⇓⇓⇓⇓⇓-12].

相对于 Max-Sum 全局等价, Max-Sum 局部等价在概率论的许多领域的应用价值更加重要. 例如, 在风险理论中, 仅仅知道索赔导致破产的可能性往往还不够, 更要关注的是相应的损失额在某个给定区间的可能性, 更深入的讨论参见 Foss^[13]. 研究 Max-Sum 局部等价的动机可追溯到 Asmussen 等人^[14] 对局部重尾分布的系统研究, 通过定义局部长尾分布族 $\mathcal{L}_{\Delta(T)}$ 和局部次指数分布族 $\mathcal{S}_{\Delta(T)}$ 的概念 (见定义 2.1), 证明了 Pareto 分布, 重尾 Weibull 分布以及对数正态分布等常见的重尾分布也属于局部次指数分布族. 此外, 他们还证明了对于独立同分布随机变量序列在条件 “对某个 $0<T\le\infty$ , 共同分布 $F\in\mathcal S_{\Delta_T}$ , 且满足 $F_i(x+\Delta_T)\sim c_i F(x+\Delta_T)$ , $c_i (1\le i\le n)$ 为非负常数” 下的部分和的局部渐近性质. 关于局部渐近性质的进一步讨论可参见文献 [15 ⇓⇓⇓-19]. 刘希军和王岳宝^[20] 研究了随机变量序列的 Max-Sum 局部等价性, 他们考虑独立不同分布随机变量序列, 在较为宽松的条件

$\begin{align*} \mbox{对任意的}\ 1\le i,j\le n, \mbox{存在某个}\ 0<T\le\infty, F_i\ast F_j\in \mathcal S_{\Delta_T} \end{align*}$

(1.3)

下得到了 Max-Sum 局部等价式. 显然, 条件 (1.3) 可以视为将条件 (1.2) 扩展为局部情形的版本. 关于相依随机变量序列的 Max-Sum 局部等价性的结果不多, 其中江涛和徐晖^[21] 研究了非负随机变量序列情形下的结果. 他们在 copula 联系函数为 Farlie-Gumbel-Morgenstern (FGM) 时, 得到了 Max-Sum 局部等价式. 该结果后来被柳福祥等人^[22]推广到实值情形.

众所周知, copula 函数在相依性建模方面是一个强有力的工具. 由 Sklar 定理可知, 随机向量的联合分布中关于各分量的相依结构完全由其对应的 copula 函数确定, 更详尽的讨论参见 Nelsen^[23]. FGM copula 因其结构简单被广泛研究, 其联系函数 $C^{FGM}$ 由下式给出: 对于任意的 $(u_1,\cdots,u_n)\in[0,1]^n$ ,

$\begin{align*} C^{FGM}(u_1,u_2,\cdots,u_n)=\prod_{i=1}^{n}u_i\Big(1+\sum\limits_{1\le k <j \le n}a_{kj}(1-u_k)(1-u_j)\Big), \end{align*}$

(1.4)

其中常数 $a_{kj}\in [-1,1], 1\leq k<j\leq n$ , 称为相依系数. 虽然 FGM copula 的结构简单, 数学上易于处理, 但是其应用也受到了很大的限制, 为此, Sancetta 和 Satchell^[24] 从闭区间有界连续函数的多项式逼近的角度提出了应用非常宽泛的 Bernstein copula 函数, 对于任意的 $(u_1,\cdots,u_n)\in[0,1]^n$ , 其表达式为

$\begin{align*} C^B(u_1,\cdots,u_n)=\sum\limits_{i_1=0}^{m}\cdots\sum\limits_{i_n=0}^{m}a\bigg(\frac{i_1}{m},\cdots,\frac{i_n}{m}\bigg)\prod_{j=1}^{n}\binom{m}{i_j}u_{j}^{i_j}(1-u_{j})^{m-i_j}, \end{align*}$

(1.5)

其中, 正整数 $m$ 称为 Bernstein 多项式的各变量的阶数. 他们证明了系数 $a(\cdot)$ 如果满足: 对于任意 $0\le i_k \le m$ , 有

$\begin{align*} \Delta_{1,\cdots,n}a\bigg(\frac{i_1}{m},\cdots,\frac{i_n}{m}\bigg):=\sum\limits_{j_1=0}^{1}\cdots\sum\limits_{j_n=0}^{1}(-1)^{j_1+\cdots+j_n}a\bigg(\frac{i_1+j_1}{m},\cdots,\frac{i_n+j_n}{m}\bigg)\ge 0 \end{align*}$

(1.6)

以及

$\begin{align*} \max\bigg\{0,\frac{i_1}{m}+\cdots+\frac{i_n}{m}-n+1\bigg\}\le a\bigg(\frac{i_1}{m},\cdots,\frac{i_n}{m}\bigg)\le \min\bigg\{\frac{i_1}{m},\cdots,\frac{i_n}{m}\bigg\}, \end{align*}$

(1.7)

那么 (1.5) 式确为 copula 函数. 通过对 (1.5) 式关于每个变量进行求导并重新排列, 得到 Bernstein copula 的密度为

$\begin{aligned} & c^{B}\left(u_{1}, \cdots, u_{n}\right) \\ = & \sum_{i_{1}=0}^{m} \cdots \sum_{i_{n}=0}^{m}(m+1)^{k} \Delta_{1, \cdots, n} a\left(\frac{i_{1}}{m+1}, \cdots, \frac{i_{n}}{m+1}\right) \prod_{j=1}^{n}\binom{m}{i_{j}} u_{j}^{i_{j}}\left(1-u_{j}\right)^{m-i_{j}} . \end{aligned}$

(1.8)

同样, Bernstein copula 具有良好的分析性质, 因此许多研究人员将 Bernstein copula 作为各种 copula 统计模型中 copula 密度函数的平滑非参数估计对象, 并研究其渐近性质, 如几乎处处收敛性和渐近正态性等, 具体参见文献 [25 ⇓-27]. Bernstein copula 在其它场景下的应用 (尤其是在金融和精算领域), 请参见文献 [28 ⇓⇓⇓-32].

本文将在 Bernstein copula 作为连接函数的条件下来研究随机变量的 Max-Sum 局部等价式. 从上一段的讨论可知对于任意有界连续的 copula 函数, 总可以用 Bernstein copula 来逼近, 这极大地扩张了 Max-Sum 局部等价式成立的范围. 本文的主要结果如下.

定理 1.1 给定 $n\geq2$ , 设非负随机变量序列 $\{X_i, 1\le i \le n\}$ 的相依结构由 Bernstein copula (1.5) 式刻画.

(1) 假设对于某个 $0<T\le\infty$ 和 $x_{0}>0$ , 若对于所有的 $x>x_{0}$ , 以及 $1\leq i\leq n$ , 有 $F_i(x+\Delta(T))>0$ , 则

$\begin{equation} F_{X_{(n)}}(x+\Delta(T))\sim \sum\limits_{i=1}^{n}F_i(x+\Delta(T)). \end{equation}$

(1.9)

(2) 此外, 进一步假设对于某个 $0<T\le\infty$ , 如果对任意的 $1\le i<j \le n$ , 有

$\begin{equation} F_i\in {\mathcal L}_{\Delta(T)}, 且 F_i\ast F_j\in{\mathcal S}_{\Delta(T)}, \end{equation}$

(1.10)

则

$\begin{equation} F_{S_n}(x+\Delta(T))\sim \sum\limits_{i=1}^{n}F_i(x+\Delta(T)). \end{equation}$

(1.11)

从而 Max-Sum 局部等价式 (1.11) 成立.

需要说明的是, 本文主要结果的证明, 既运用了“一次大跳”原理, 也充分挖掘了 Bernstein copula 的相关性质. 另外, 沿用刘希军和王岳宝^[20] 的处理方法, 将会在一定条件下得到实值情形下的 Max-Sum 局部等价式, 限于篇幅, 本文不作展开. 本文的其余部分结构如下: 第 2 节介绍符号和预备知识, 包括 Bernstein copula 和局部重尾分布族的一些重要性质. 第 3 节给出主要结果的具体证明. 第 4 节给出相应的数值实验结果.

2 符号和预备知识

为表达简洁, 本节首先介绍证明中需要的相关记号, 类似的记号约定参见龚婵^[33]. 对任意正整数 $m$ , $n$ 和 $k$ , 其中 $1\le k \le n$ , 对定义在 $\left\{1,\cdots,m\right\}^{n}$ 上的实值函数 $f$ , 依次约定

$\begin{align*} &(i_1,\cdots,i_n) := \boldsymbol{i},\\ &(1,\cdots,1) := \boldsymbol{1},\\ &(i_1,\cdots,i_{k-1},i_{k+1},\cdots,i_n) := \boldsymbol{i}_{-k},\\ &\sum\limits_{i_1=1}^{m}\cdots\sum\limits_{i_n=1}^{m}f(i_1,\cdots,i_n) := \sum\limits_{\boldsymbol{i}}f(\boldsymbol{i}),\\ &\sum\limits_{i_1=1}^{m}\cdots\sum\limits_{i_{k-1}=1}^{m}\sum\limits_{i_{k+1}=1}^{m}\cdots\sum\limits_{i_n=1}^{m}f(i_1,\cdots,i_n) := \sum\limits_{\boldsymbol{i}_{-k}}f(\boldsymbol{i}). \end{align*}$

如果给定 $i_{k}=l$ , 则记 $f(i_1,\cdots,i_{k-1},l,i_{k+1},\cdots,i_n):=f(\boldsymbol{i}_{-k},l)$ . 类似地, 对于任意实变量多元函数 $g(\boldsymbol{u}):=g(u_1,\cdots,u_n)$ , 如果给定 $u_{k}=u$ , 则记

$\begin{eqnarray*} g(u_1,\cdots,u_{k-1},u,u_{k+1},\cdots,u_n):=g(\boldsymbol{u}_{-k},u). \end{eqnarray*}$

对于给定的 $n$ 元 copula 函数 $C(\boldsymbol{u})$ , 若对其自变量 $\boldsymbol{u}=(u_1,\cdots,u_n)\in[0,1]^{n}$ 的第 $k$ 个分量 $u_{k}$ 求一阶偏导数, 则记

$\begin{eqnarray*} \mathrm{D}C_k(\boldsymbol{u}):=\frac{\partial C(u_1,\cdots,u_n)}{\partial u_k}, \end{eqnarray*}$

若对除第 $k$ 个变量之外的其余自变量求 $k-1$ 阶偏导数, 则记

$\begin{eqnarray*} \mathrm{D}C_{-k}(\boldsymbol{u}):=\frac{\partial C(u_1,\cdots,u_n)}{\partial u_1\cdots\partial u_{k-1}\partial u_{k+1}\cdots\partial u_{n}}. \end{eqnarray*}$

采用上述记号, 则 (1.5) 式中的 Bernstein copula 可改写为

$\begin{align*} C^B(\boldsymbol{u})=\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})u_1^{i_1}\cdots u_n^{i_n}, \boldsymbol{u}\in[0,1]^n. \end{align*}$

(2.1)

通过比较 (1.5) 式和 (2.1) 式的系数, 有

$\begin{equation} \begin{split} c(\boldsymbol{i}) = & \sum\limits_{j_1=1}^{i_1}\cdots\sum\limits_{j_n=1}^{i_n}(-1)^{i_1-j_1+\cdots +i_n-j_n} \\ & \cdot a\bigg(\frac{j_1}{m},\cdots,\frac{j_n}{m}\bigg)\binom{m}{j_1}\cdots\binom{m}{j_n}\binom{m-j_1}{i_1-j_1}\cdots\binom{m-j_n}{i_n-j_n}. \end{split} \end{equation}$

(2.2)

由 (2.1) 式容易看出, FGM copula (1.4) 是 Bernstein copula 当 $m=2$ 时的特例, 由 (2.2) 式容易看出系数 $c(\boldsymbol{i})$ 满足对称性和可交换性. 另外, 由 $C^{B}(\boldsymbol{1})=1$ 可得 $\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})=1$ . 下面的引理 2.1 描述了 Bernstein copula 系数 $c(\boldsymbol{i})$ 的一个重要性质, 它在证明主要结果时发挥了关键作用.

引理 2.1 给定 $n\ge 2$ , 对 $n$ 元 Bernstein copula 函数 (2.1) 式和任意的 $1\le k\le n$ , 有

$\begin{equation} \sum\limits_{\boldsymbol{i}_{-k}}c(\boldsymbol{i}) =\begin{cases} 1,&\quad i_k=1,\\ 0,&\quad i_k=2,\cdots,n. \end{cases} \end{equation}$

(2.3)

证根据 copula 函数的性质, (2.1) 式可视为边缘分布均服从 [0,1] 上均匀分布的随机向量 $\boldsymbol{U}=(U_1,\cdots,U_n)$ 的联合分布函数, 从而对于任何给定的 $u_{k}\in(0,1)$ 有

$\begin{align*} P(\boldsymbol{U}_{-k} \le \boldsymbol{1}_{-k} \vert U_k =u_k)=1. \end{align*}$

上式等价于

$\begin{equation*} \mathrm{D}C_k^{B}(\boldsymbol{1}_{-k},u_k)=\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_k u_k^{i_k-1}=1, 1\le i_k\le m. \end{equation*}$

令 $i_k= 1$ , 有

$\begin{eqnarray*} \sum\limits_{\boldsymbol{i}_{-k}}c(\boldsymbol{i}_{-k},1)=1. \end{eqnarray*}$

因此, 当 $i_k=1$ 时, (2.3) 式成立. 进而有

$\begin{align*} \sum\limits_{i_k=2}^{m}\Big(i_k\sum\limits_{\boldsymbol{i}_{-k}}c(\boldsymbol{i})\Big)u_k^{i_k-1}=0. \end{align*}$

(2.4)

注意到 $\{u_k, u_k^{2}, \cdots, u_k^{m-1}\}$ 在多项式函数空间中是线性无关的, 这意味着(2.4) 式中的所有系数都等于零. 故对任意的 $i_k\in\{2,\cdots,m\}$ , 有

$\begin{align*} \sum\limits_{\boldsymbol{i}_{-k}}c(\boldsymbol{i})=\sum\limits_{\boldsymbol{i}_{-k}}c(\boldsymbol{i}_{-k},i_k)=0. \end{align*}$

引理 2.1 证毕.

引理 2.1 将 Coqueret^[34] 的结果推广到了 $n$ 元 Bernstein copula 的情形. Coqueret^[34] 证明了对于二元情形

$\begin{align*} C^B(u_1,u_2)=\sum\limits_{i_1=1}^{m}\sum\limits_{i_2=1}^{m}c(i_1,i_2)u_1^{i_1}u_2^{i_2}, (u_1,u_2)\in[0,1]^2, \end{align*}$

(2.5)

(2.3) 式成立. 此时,

$\begin{align*} && \sum\limits_{i_2=1}^{m}c(1,i_2)=\sum\limits_{i_1=1}^{m}c(i_1,1)=1, \end{align*}$

(2.6)

$\begin{align*} &&\sum\limits_{i_2=1}^{m}c(k,i_2)=\sum\limits_{i_1=1}^{m}c(i_1,k)=0, k\in\{2,\cdots,n\}. \end{align*}$

(2.7)

引理 2.2 如果二维随机变量 $(X_1,X_2)$ 的连接函数由 Bernstein copula (2.5) 式确定, 那么对任意的 $x_i\in \mathbb{R}$ 和 $T_i\in (0,\infty]$ , $i=1,2$ , 存在正常数 $C$ , 使得

$\begin{align*} P(X_1\in x_1+\Delta(T_1),X_2\in x_2+\Delta(T_2))\leq C P(X_1\in x_1+\Delta(T_1))P(X_2\in x_2+\Delta(T_2)).\,\,\,\,\,\, \end{align*}$

(2.8)

证注意到

$\begin{eqnarray*} &&P(X_1\in x_1+\Delta(T_1),X_2\in x_2+\Delta(T_2))\\ &=&[P(X_1\le x_1+T_1,X_2\le x_2+T_2)-P(X_1\le x_1+T_1,X_2\le x_2)]\\ &&-P(X_1\le x_1,X_2\le x_2+T_2)-P(X_1\le x_1,X_2\le x_2) :=\mathrm{I}_1-\mathrm{I}_2. \end{eqnarray*}$

根据 (2.5) 式, 有

$\begin{matrix} \mathrm{I}_1 &=&C^B(F_1(x_1+T_1),F_2(x_2+T_2))-C^B(F_1(x_1+T_1),F_2(x_2))\nonumber\\ &=&\sum\limits_{i_1=1}^{m}\sum\limits_{i_2=1}^{m}c(i_1,i_2)F_1^{i_1}(x_1+T_1)F_2^{i_2}(x+T_2)-\sum\limits_{i_1=1}^{m}\sum\limits_{i_2=1}^{m}c(i_1,i_2)F_1^{i_1}(x_1+T_1)F_2^{i_2}(x_2)\nonumber\\ &=&\sum\limits_{i_1=1}^{m}\sum\limits_{i_2=1}^{m}c(i_1,i_2)F_1^{i_1}(x_1+T_1)F_2(x_2+\Delta(T_2))(F_2^{i_2-1}(x_2+T_2)+\cdots+F_2^{i_2-1}(x_2)),\,\,\,\,\,\,\,\, \end{matrix}$

(2.9)

最后一步根据公式 $a^i-b^i=(a-b)(a^{i-1}+\cdots+a^{i-j}b^{j}+\cdots+b^{i-1})$ 得到. 类似地,

$\begin{align*} \mathrm{I}_2 &=&\sum\limits_{i_1=1}^{m}\sum\limits_{i_2=1}^{m}c(i_1,i_2)F_1^{i_1}(x_1)F_2(x_2+\Delta(T_2))(F_2^{i_2-1}(x_2+T_2)+\cdots+F_2^{i_2-1}(x_2)). \end{align*}$

(2.10)

用 (2.9) 式减去 (2.10) 式, 有

$\begin{eqnarray*} &&P(X_1\in x_1+\Delta(T_1),X_2\in x_2+\Delta(T_2))\nonumber\\ &=&\sum\limits_{i_1=1}^{m}\sum\limits_{i_2=1}^{m}c(i_1,i_2)F_1(x_1+\Delta(T_1))F_2(x_2+\Delta(T_2))(F_1^{i_1-1}(x_1+T_1)+\cdots+F_1^{i_1-1}(x_1))\nonumber\\ && \times(F_2^{i_2-1}(x_2+T_{2})+\cdots+F_2^{i_2-1}(x_2))\nonumber\\ &\le&\Big(m^2\sum\limits_{i_1=1}^{m}\sum\limits_{i_2=1}^{m}|c(i_1,i_2)|\Big)F_1(x_1+\Delta(T_1))F_2(x_2+\Delta(T_2)), \end{eqnarray*}$

引理 2.2 证毕.

接下来, 介绍一些局部重尾分布族的概念. 更详尽的讨论可参见 Asmussen 等人^[14].

定义 2.1 设分布 $F$ 定义在 $(-\infty,+\infty)$ 上, $T>0$ 为给定的常数. 如果对所有的 $t\in[0,1]$ 一致成立

$\begin{eqnarray*} F(x+t+\Delta(T))\sim F(x+\Delta(T)), \end{eqnarray*}$

则称分布 $F$ 为 $(-\infty,+\infty)$ 上的局部长尾族, 记作 $F\in \mathcal{L}_{\Delta(T)}$ . 如果 $F$ 定义在 $[0,\infty)$ 上, $F\in \mathcal{L}_{\Delta(T)}$ , 且满足

$\begin{eqnarray*} F^{2*}(x+\Delta(T))\sim 2F(x+\Delta(T)), \end{eqnarray*}$

则称分布 $F$ 为 $[0,\infty)$ 上的局部次指数族, 记作 $F\in \mathcal{S}_{\Delta(T)}$ , 这里 $F^{2*}$ 是 $F$ 的二重卷积.

在此指出的是, 对于 $[0,\infty)$ 上的局部次指数族而言, 条件 $F\in \mathcal{L}_{\Delta(T)}$ 不可或缺, 与之形成对比的是, 对于 $[0,\infty)$ 上的次指数分布族, 对应的长尾条件是自动成立的. 至于如何将局部次指数族的定义推广到实值情形, 更深入的讨论可见文献 [35]. 另外, 对于任意给定的 $0<T\le \infty$ , 如果 $F\in \mathcal{L}_{\Delta(T)}$ , 那么

$\begin{eqnarray*} \mathcal{H}_{\Delta(T)}(F)&=&\Big\{h: h(x)\uparrow\infty, h(x)=o(x), \mbox{且对于所有的}\ |t|\leq h(x)\ \mbox{一致成立}\\&&F(x+t+\Delta(T))\sim F(x+\Delta(T))\Big\}\neq\emptyset. \end{eqnarray*}$

如果 $h_1\in{\mathcal H}_{\Delta(T)}(F)$ , $h_2\le h_1$ 且 $h_2(x)\uparrow\infty$ , 则 $h_2\in{\mathcal H}_{\Delta(T)}(F)$ . 因此, 如果 $F_i\in{\mathcal L}_{\Delta(T)}$ , $i=1,2$ , 那么 $\mathcal{H}_{\Delta(T)}(F_1)\cap\mathcal{H}_{\Delta(T)}(F_2)\neq\emptyset$ .

下面的引理 2.3 来自文献 [21,引理 2.2,2.3] 的等价描述.

引理 2.3 对固定的 $0<T\le\infty$ , 如果定义在 $[0,\infty)$ 上的 $F_i\in\mathcal L_{\Delta(T)}$ , $i=1,2$ , 且 $F_1\ast F_2\in \mathcal{S}_{\Delta(T)}$ , 那么对于任意的 $h\in\mathcal H_{\Delta(T)}(F_1)\bigcap\mathcal H_{\Delta(T)}(F_2)$ , 如下两命题等价

$\begin{align*} &(1) F_1 \ast F_2(x+\Delta(T)) \sim F_1(x+\Delta(T)) + F_2(x+\Delta(T)); \nonumber\\ &(2) \int_{h(x)}^{x-h(x)}\overline{F_1}(x-y+\Delta(T))F_2(\mathrm{d}y) = o(F_1(x+\Delta(T)) + F_2(x+\Delta(T))); \end{align*}$

(2.11)

另外, 如果 $F_i\in\mathcal S_{\Delta(T)}$ , $i=1,2$ , 则 (2.11) 式蕴含 $F_1*F_2\in\mathcal S_{\Delta(T)}$ .

3 定理 1.1 的证明

3.1 定理 1.1 (1) 的证明

证将 $F_{X_{(n)}}(x+\Delta)$ 分解为

$\begin{aligned} & F_{X_{(n)}}(x+\Delta(T)) \\ = & \sum_{i=1}^{n} P\left(X_{i} \in x+\Delta(T), X_{l} \leq x, 1 \leq l \neq i \leq n\right) \\ & +\sum_{1 \leq i_{1}＜i_{2} \leq n} P\left(X_{i_{1}} \in x+\Delta(T), X_{i_{2}} \in x+\Delta(T), X_{l} \leq x, l \in\{1,2, \cdots, n\} \backslash\left\{i_{1}, i_{2}\right\}\right) \\ & +\cdots+P\left(X_{i} \in x+\Delta(T), 1 \leq i \leq n\right) \\ := & \sum_{i=1}^{n} P_{i}(x)+\sum_{1 \leq i_{1}＜i_{2} \leq n} P_{i_{1}, i_{2}}(x)+\cdots+P_{1,2, \cdots, n}(x). \end{aligned}$

(3.1)

首先处理 $P_i(x)$ , $1\le i\le n$ . 注意到

$\begin{align*} P_i(x)=P(X_i\in x+\Delta(T))-P\bigg(X_i\in x+\Delta(T), \bigcup_{1\le l \neq i\le n}\{X_l>x\}\bigg), \end{align*}$

(3.2)

根据引理 2.2, 存在正常数 $C$ , 对所有的 $1\le i \ne l \le n$ 有

$\begin{eqnarray*} &&P\bigg(X_i\in x+\Delta(T), \bigcup_{1\le l \neq i\le n}\left \{X_l>x \right \}\bigg)\\ &\le&\sum\limits_{1\le l \neq i\le n} P(X_i\in x+\Delta(T), X_l>x)\\ &\le&C\sum\limits_{1\le l \ne i\le n}P(X_i\in x+\Delta(T))P(X_l> x)\\ &\le&CP(X_l> x)\sum\limits_{i=1}^{n}P(X_i\in x+\Delta(T))=o\left(\sum\limits_{i=1}^{n}F_i(x+\Delta(T))\right). \end{eqnarray*}$

结合 (3.2) 式, 有

$\begin{align*} \sum\limits_{i=1}^{n}P_i(x)\sim \sum\limits_{i=1}^{n}F_i(x+\Delta(T)). \end{align*}$

(3.3)

再处理 (3.1) 式余下部分. 显然, 对于任意的 $1\le i_1<i_2<\cdots <i_l\le n,\ 2\le l \le n$ , 有

$\begin{align*} P_{i_1,\cdots,i_l}(x)\le P(X_{i_1}\in x+\Delta(T),\ X_{i_2}\in x+\Delta(T))=o\left(\sum\limits_{i=1}^{n}F_i(x+\Delta(T))\right). \end{align*}$

(3.4)

结合 (3.1) 式, (3.3) 式和 (3.4) 式, 立得 (1.9) 式.

3.2 定理 1.1 (2) 的证明

证采用数学归纳法来证明对于任何 $n\ge 2$ , 成立 (1.11) 式和

$\begin{align*} P(S_n\in {x+\Delta(T)},X_i>h(x),1\le i \le n)&=&o\left(\sum\limits_{i=1}^{n}F_i(x+\Delta(T))\right), \end{align*}$

(3.5)

其中, $h\in \bigcap\limits_{i=1}^{n}\mathcal H_{\Delta(T)}(F_i)$ .

首先, 当 $n=2$ 时, 任取 $h\in\mathcal H_{\Delta(T)}(F_1)\bigcap\mathcal H_{\Delta(T)}(F_2)\bigcap\mathcal H_{\Delta(\infty)}(F_1)\bigcap\mathcal H_{\Delta(\infty)}(F_2)$ , 将 $P(S_2\in x+\Delta )$ 分割成如下三部分

$\begin{aligned} P\left(S_{2} \in x+\Delta(T)\right) \leq & P\left(S_{2} \in x+\Delta(T), X_{1} \leq h(x)\right)+P\left(S_{2} \in x+\Delta(T), X_{2} \leq h(x)\right) \\ & +P\left(S_{2} \in x+\Delta(T), X_{1}>h(x), X_{2}>h(x)\right) \\ := & P_{2,1}(x)+P_{2,2}(x)+P_{2,3}(x). \end{aligned}$

(3.6)

对于 $P_{2,1}(x)$ , 简单计算表明

$\begin{eqnarray*} P_{2,1}(x)\nonumber &=&\int_{0}^{h(x)}P(x-x_1\leq X_2\leq x+T-x_1|X_1=x_1 )F_1(\mathrm{d}x_1)\nonumber\\ &=&\int_{0}^{h(x)}\Big(\mathrm{D}C_{1}^{B}(F_1(x_1),F_2(x+T-x_1))-\mathrm{D}C_{1}^{B}(F_1(x_1),F_2(x-x_1)) \Big)F_1(\mathrm{d}x_1)\nonumber\\ &=&\int_{0}^{h(x)} \sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})F_{1}^{i_1-1}(x_1)(F_{2}^{i_2}(x+T-x_1)-F_{2}^{i_2}(x-x_1))F_1(\mathrm{d}x_1)\nonumber\\ &=&\int_{0}^{h(x)}F_2(x-x_1+\Delta(T))\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})F_{1}^{i_1-1}(x_1)\nonumber\\ &&\cdot \left(F_{2}^{i_2-1}(x+T-x_1)+\cdots +F_{2}^{i_2-1}(x-x_1)\right) F_1(\mathrm{d}x_1). \end{eqnarray*}$

注意到 $U:=F_1(X_1)$ 服从 [0,1] 上的均匀分布, 因此对于每个正整数 $k$ , 都有 $E(U^k)=\frac{1}{k+1}$ . 根据该事实, 以及 $F\in \mathcal{L}_{\Delta(T)}$ , (2.6) 式和 (2.7) 式, 得到

$\begin{aligned} P_{2,1}(x) & \sim F_{2}(x+\Delta(T)) \int_{0}^{\infty} \sum_{i_{1}=1}^{m} \sum_{i_{2}=1}^{m} i_{1} i_{2} c\left(i_{1}, i_{2}\right) F_{1}^{i_{1}-1}\left(x_{1}\right) F_{1}\left(\mathrm{~d} x_{1}\right) \\ & =F_{2}(x+\Delta(T)) \sum_{i_{2}=1}^{m} i_{2}\left(\sum_{i_{1}=1}^{m} i_{1} c\left(i_{1}, i_{2}\right) E\left(U^{i_{1}-1}\right)\right) \\ & =F_{2}(x+\Delta(T))\left(\sum_{i_{1}=1}^{m} c\left(i_{1}, 1\right)+2 \sum_{i_{1}=1}^{m} c\left(i_{1}, 2\right)+\cdots+m \sum_{i_{1}=1}^{m} c\left(i_{1}, m\right)\right) \\ & =F_{2}(x+\Delta(T)) . \end{aligned}$

(3.7)

类似地,

$\begin{align*} P_{2,2}(x)\sim F_1(x+\Delta(T)). \end{align*}$

(3.8)

对于 $P_{2,3}(x)$ , 根据引理 2.3, 可得

$\begin{matrix} P_{2,3}(x) &\le&P(S_2\in x+\Delta(T),X_1>h(x),h(x)<X_2\leq x-h(x)+T) \\ &\le&\int_{h_1(x)}^{x-h_1(x)}P(x-x_2\leq X_1\leq x+T-x_2|X_2=x_2)F_2(\mathrm{d}x_2) \\ &=&\int_{h_1(x)}^{x-h_1(x)}\Big(\mathrm{D}C_{2}^{B}(F_1(x+T-x_2),F_2(t_2))-\mathrm{D}C_{2}^{B}(F_1(x-x_2),F_2(x_2)) \Big)F_2(\mathrm{d}x_2) \\ &=&\int_{h_1(x)}^{x-h_1(x)}F_1(x+\Delta(T))\Big(\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}ijc(i,j)F_2^{j-1}(x)\Big)F_2(\mathrm{d}x_2) \\ &=&O\left(\int_{h_1(x)}^{x-h_1(x)}F_{1}(x-t_2+\Delta(T))F_2(\mathrm{d}x_2)\right) \\ &=& o(F_1(x+\Delta(T))+F_2(x+\Delta(T))), \end{matrix}$

(3.9)

其中 $h_1(x)=h(x)-T$ . 综合 (3.7)-(3.9) 式, 证明了 $n=2$ 时 (1.11) 式和 (3.5) 式成立.

现假设对于所有的 $2\le k \le n-1$ , (1.11) 式和 (3.5) 式成立, 往证 (1.11) 式对 $k=n$ 成立. 任取 $h\in \bigcap\limits_{i=1}^{n}\mathcal H_{\Delta(T)}(F_i)$ , 对于充分大的 $x$ , 将 $P(S_n\in x+\Delta(T))$ 分割为

$\begin{aligned} F_{S_{n}}(x+\Delta(T)) & =\sum_{l=1}^{n} P\left(S_{n} \in x+\Delta(T), \min _{1 \leq j \leq l} X_{i_{j}}>h(x), \max _{s \in\{1,2, \cdots, n\} \backslash\left\{i_{1}, \cdots, i_{l}\right\}} X_{s} \leq h(x)\right) \\ & :=\sum_{l=1}^{n} \sum_{1 \leq i_{1}＜i_{2}＜\cdots＜i_{l} \leq n} P_{n,\left\{i_{1}, \cdots, i_{l}\right\}}(x) . \end{aligned}$

(3.10)

由对称性, 只需考虑对任意的 $1\le l \le n$ , $\{i_1,\cdots,i_l\}=\{1,\cdots,l\}$ 的情况. 先处理 $P_{n,\{1\}}(x)$ . 为方便, 令 $T_1=t_2+\cdots+t_n$ , 此时有

$\begin{align*} &P_{n,\{1\}}(x)\\ &=P(S_n\in{x+\Delta(T)},X_1> h(x),X_2\leq h(x),\cdots,X_n\leq h(x))\\ =&\int_{[h(x)]^{n-1}}P(x-T_1 \leq X_1<x+T-T_1|X_2=t_2,\cdots,X_n=t_n)\prod_{i=2}^{n}F_i(\mathrm{d}t_i)\\ =&\int_{[h(x)]^{n-1}}\frac{\mathrm{D}C^B_{-1}(F_1(x+T-T_1),\boldsymbol{u}_{-1})-\mathrm{D}C^B_{-1}(F_1(x-T_1),\boldsymbol{u}_{-1})}{\mathrm{D}C^B_{-1}(1,\boldsymbol{u}_{-1})}\Big|_{\boldsymbol{u}_{-1}=(F_i(t_i), 2\leq i\leq n)}\nonumber\\ & \cdot\prod_{i=2}^{n}F_i(\mathrm{d}t_i). \end{align*}$

注意到

$\begin{eqnarray*} \mathrm{D}C^B_{-1}(\boldsymbol{u})=\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_2\cdots i_nu_1^{i_1}u_2^{i_2-1}\cdots u_n^{i_n-1}, \end{eqnarray*}$

再根据 (2.1) 式, 有

$\begin{eqnarray*} \mathrm{D}C^B_{-1}(1,\boldsymbol{u}_{-1})=\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_2\cdots i_nu_2^{i_2-1}\cdots u_n^{i_n-1}. \end{eqnarray*}$

将被积函数简化为

$\begin{align*} &\ \ \ \ \ \frac{\mathrm{D}C^B_{-1}(F_1(x+T-T_1),\boldsymbol{u}_{-1})-\mathrm{D}C^B_{-1}(F_1(x-T_1),\boldsymbol{u}_{-1})}{\mathrm{D}C^B_{-1}(1,\boldsymbol{u}_{-1})}\nonumber\\ &=\frac{F_1(x-T_1+\Delta)\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_2\cdots i_nu_2^{i_2-1}\cdots u_n^{i_n-1}(F_1^{i_1-1}(x+T-T_1)+\cdots +F_1^{i_1-1}(x-T_1))}{\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_2\cdots i_nu_2^{i_2-1}\cdots u_n^{i_n-1}}. \end{align*}$

由 $F_1\in \mathcal{L}_{\Delta(T)}$ 可知, 对于充分大的 $x$ , 有

$\begin{align*} & P_{n,\{1\}}(x)\nonumber\\&\sim F_1(x+\Delta(T))\int_{[\infty]^{n-1}} \frac{\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_1i_2\cdots i_nu_2^{i_2-1}\cdots u_n^{i_n-1}}{\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_2\cdots i_nu_2^{i_2-1}\cdots u_n^{i_n-1}}\Big|_{\boldsymbol{u}_{-1}=(F_i(t_i), 2\leq i\leq n)}\cdot\prod_{i=2}^{n}F_i(\mathrm{d}t_i)\nonumber\\ &\ge F_1(x+\Delta(T))\int_{[\infty]^{n-1}} \prod_{i=2}^{n}F_i(\mathrm{d}t_i)\nonumber\\ & = F_1(x+\Delta(T)), \end{align*}$

(3.11)

上面的第二步利用了不等式: 如果 $\frac{a_i}{b_i}>0$ , $i=1,\cdots,n$ , 则有

$\begin{align*} \min_{1\le i \le n}\frac{a_i}{b_i}\le \frac{\sum\limits_{i=1}^{n}a_i}{\sum\limits_{i=1}^{n}b_i}\le \max\limits_{1\le i \le n} \frac{a_i}{b_i}. \end{align*}$

下证明对 $P_{n,\{1\}}(x)$ , 反向渐近关系式也成立. 对任意 $\epsilon>0$ , 令

$\begin{eqnarray*} A_{\epsilon}=\{(t_2,\cdots,t_n)\mid \mathrm{D}C^B_{-1}(F_2(t_2),\cdots,F_n(t_n))\ge \epsilon\}, \end{eqnarray*}$

有

$\begin{align*} & \quad \int_{[\infty]^{n-1}} \frac{\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_1i_2\cdots i_nu_2^{i_2-1}\cdots u_n^{i_n-1}}{\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_2\cdots i_nu_2^{i_2-1}\cdots u_n^{i_n-1}}\Big|_{\boldsymbol{u}_{-1}=(F_i(t_i), 2\leq i\leq n)}\prod_{i=2}^{n}F_i(\mathrm{d}t_i)\nonumber\\ &= 1+\int_{A_{\epsilon}\cup A_{\epsilon}^{c}}\frac{\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})(i_1-1)i_1i_2\cdots i_nu_2^{i_2-1}\cdots u_n^{i_n-1}}{\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_2\cdots i_nu_2^{i_2-1}\cdots u_n^{i_n-1}}\Big|_{\boldsymbol{u}_{-1}=(F_i(t_i), 2\leq i\leq n)}\prod_{i=2}^{n}F_i(\mathrm{d}t_i)\nonumber\\ &\le 1+\frac{1}{\epsilon} \sum\limits_{i_1=2}^{m}(i_1 -1)\sum\limits_{\boldsymbol{i}_{-1}}c(\boldsymbol{i})\int_{[0,1]^{n-1}}i_2\cdots i_nu_2^{i_2-1}\cdots u_n^{i_n-1}\prod_{i=2}^{n}\mathrm{d}u_i+\int_{A_{\epsilon}^{c}}(m-1)\prod_{i=2}^{n}F_i(\mathrm{d}t_i)\nonumber\\ &= 1+\frac{1}{\epsilon}\sum\limits_{i_1=2}^{m}(i_1 -1)\sum\limits_{\boldsymbol{i}_{-1}}c(\boldsymbol{i})\prod_{j=2}^{n}(i_j \int_{0}^{1}u_n^{i_j-1})\mathrm{d}u_j+(m-1)P(A_{\epsilon}^{c})\nonumber\\ &= 1+\frac{1}{\epsilon}\sum\limits_{i_1=2}^{m}(i_1 -1)\sum\limits_{\boldsymbol{i}_{-1}}c(\boldsymbol{i})+(m-1)P(A_{\epsilon}^{c})\nonumber\\ &= 1+(m-1)P(A_{\epsilon}^{c})\rightarrow 1,\quad \epsilon\downarrow 0. \end{align*}$

(3.12)

由 (3.11) 式和 (3.12) 式, 得

$\begin{align*} P_{n,\{1\}}(x)\sim F_1(x+\Delta(T)). \end{align*}$

(3.13)

再考虑 $l=n$ 的情形. 给定 $X_i=t_i,1\le i\le n-1$ , 记 $t_n=x-\sum\limits_{i=1}^{n-1}t_i$ , $A_{n-1}(x,T)=\{(t_1,\cdots,t_{n-1})\mid t_i>h(x),1\le i\le n-1,\sum\limits_{i=1}^{n-1}t_i\le x-h(x)+T\}$ , 对于充分大的 $x$ , 用类似处理 (3.13) 式的方法, 可得

$\begin{align*} &\quad\,\, P_{n,\{1,2,\cdots,n\}}(x)\nonumber\\&=P(S_n\in x+\Delta(T),X_i>h(x),1\le i\le n)\nonumber\\ &\le P(S_n\in x+\Delta(T),(X_1,\cdots,X_{n-1})\in A_{n-1}(x,T))\nonumber\\ &=\int_{A_{n-1}(x,T)}P(X_n\in t_n +\Delta(T)|X_i=t_i,1\le i\le n-1) \prod_{i=1}^{n-1}F_i(\mathrm{d}t_i)\nonumber\\ &=\int_{A_{n-1}(x,T)}\frac{\mathrm{D}C^B_{-n}(\boldsymbol{u}_{-n},F_n(t_n+T))-\mathrm{D}C^B_{-n}(\boldsymbol{u}_{-n},F_n(t_n))}{\mathrm{D}C^B_{-n}(1,\boldsymbol{u}_{-n})}\Big|_{\boldsymbol{u}_{-n}=(F_i(t_i),1\le i \le n-1)} \prod_{i=1}^{n-1}F_i(\mathrm{d}t_i)\nonumber\\ &\le\int_{A_{n-1}(x,T)}F_n(t_n+\Delta(T))\frac{\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_1i_2\cdots i_nu_1^{i_1-1}\cdots u_{n-1}^{i_{n-1}-1}}{\sum\limits_{\boldsymbol{i}}c(\boldsymbol{i})i_1\cdots i_{n-1}u_1^{i_1-1}\cdots u_{n-1}^{i_{n-1}-1}}\Big|_{\boldsymbol{u}_{-n}=(F_i(t_i),1\le i \le n-1))} \prod_{i=1}^{n-1}F_i(\mathrm{d}t_i)\nonumber\\ &\le m\int_{A_{n-1}(x,T)}F_n(t_n+\Delta(T))\prod_{i=1}^{n-1}F_i(\mathrm{d}t_i) =O\Big(\int_{A_{n-1}(x,T)}F_n(t_n+\Delta(T))\prod_{i=1}^{n-1}F_i(\mathrm{d}t_i)\Big). \end{align*}$

现设 $X_n^*$ 是一个与 $X_n$ 独立同分布的随机变量, 根据 (1.10) 式和归纳假设知, 对于充分大的 $x$ , 有

$\begin{matrix} P_{n,\{1,2,\cdots,n\}}(x) &=&O\Big(P(S_{n-1}+X_n^*\in x+\Delta(T),h(x)-T<S_{n-1}\le x-h(x)+T)\Big)\nonumber\\ &=&O\Big(P(S_{n-1}+X_n^*\in x+\Delta(T),h(x)-T<X_n^*\le x-h(x)+T)\Big)\nonumber\\ &=&O\Big(\int_{h_1(x)}^{x-h_1(x)}P(S_{n-1}\in x-u_n+\Delta(T))P(X_n^*\in \mathrm{d}u_n)\Big)\nonumber\\ &=&O\Big(\sum\limits_{i=1}^{n-1}\int_{h_1(x)}^{x-h_1(x)}F_i(x+\Delta(T))F_n(\mathrm{d}u_n)\Big)\nonumber\\ &=&o\Big(\overline{F}_i(x+\Delta(T))+F_n(x+\Delta(T))\Big) =o\Big(\sum\limits_{i=1}^{n}F_i(x+\Delta(T))\Big). \end{matrix}$

(3.14)

最后, 考虑 $2\le l\le n-1$ 的情形. 显然对任意的 $1\le i\le n$ , $F_i\in \mathcal{L}_{\Delta(T)}$ . 由归纳假设可知

$\begin{aligned} P_{n,\{1, \cdots, l\}}(x) & =\int_{[0, h(x)]^{n-l}} P\left(S_{l} \in x-\sum_{j=l+1}^{n} t_{j}+\Delta(T), X_{i}>h(x), 1 \leq i \leq l\right) \prod_{j=l+1}^{n} F_{j}\left(\mathrm{d} t_{j}\right) \\ & =\int_{[0, \infty)^{n-l}} o\left(\sum_{i=1}^{l} F_{i}(x+\Delta(T))\right) \prod_{j=l+1}^{n} F_{j}\left(\mathrm{~d} t_{j}\right) \\ & =o\left(\sum_{i=1}^{n} F_{i}(x+\Delta(T))\right) . \end{aligned}$

(3.15)

综合 (3.10)-(3.15) 式, 可知当 $k=n$ 时 (1.11) 式成立. 定理 1.1 证毕.

4 数值实验

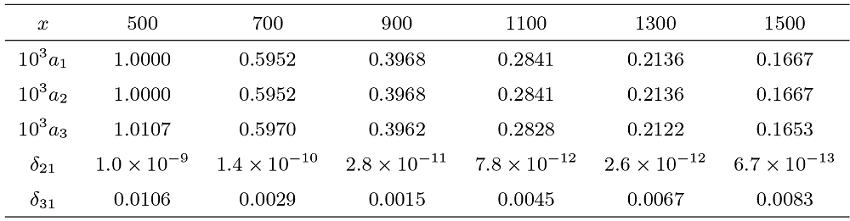
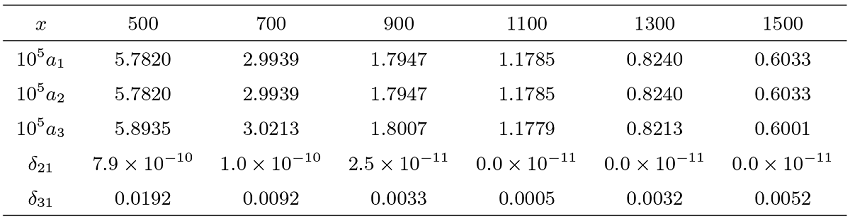
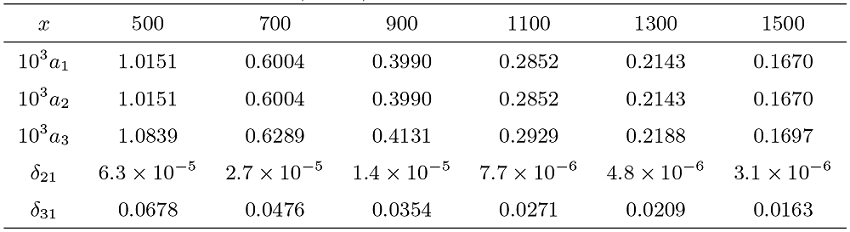
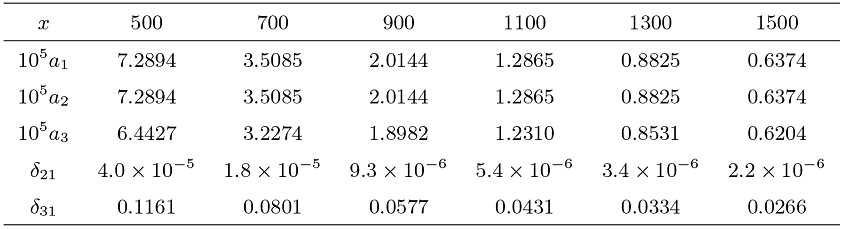
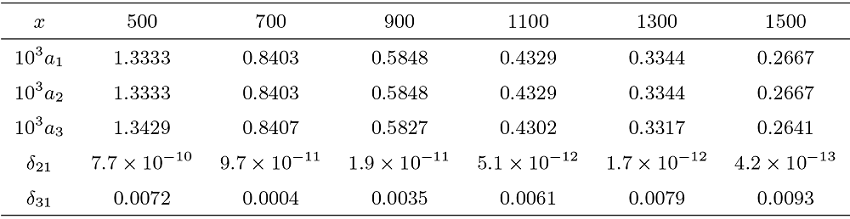
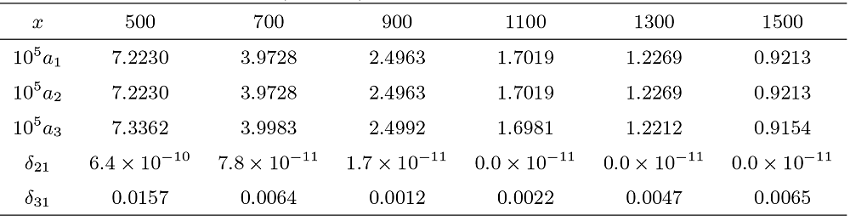
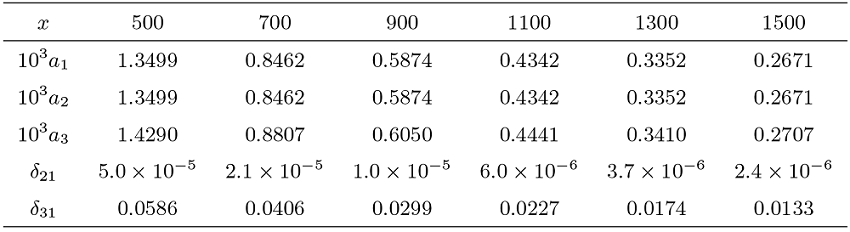
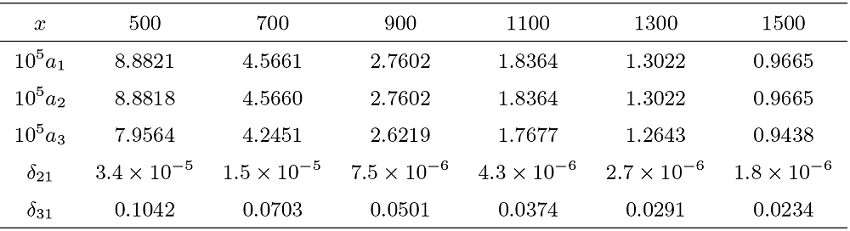
本节通过数值实验来进一步考察定理 1.1 结论的近似效果, 验证 Max-Sum 局部等价式的可行范围. 为了方便, 我们仅考虑二维情形. 假定随机变量 $X_1$ 服从对数正态分布,其密度为

$\begin{align*} f_1(x;\mu,\sigma) =\begin{cases} \frac{1}{x\sqrt{2\pi}\sigma}\mathrm{exp}\Big[-\frac{1}{2\sigma^2}\left(\mathrm{ln}x-\mu\right)^2\Big],&\quad x>0,\\ 0,&\quad x\leq0, \end{cases} \end{align*}$

其参数 $\mu \in \mathbb{R}, \sigma>0$ . 对应的分布函数为

$\begin{align*} F_{1}\left( x;\lambda,\sigma \right) =\Phi \left( \dfrac{\mathrm{ln}x-\mu }{\sigma}\right), \end{align*}$

其中 $\Phi(\cdot)$ 表示标准正态分布. 随机变量 $X_2$ 服从 Pareto 分布, 其密度为

$\begin{align*} f_2(x;\lambda,k) = \begin{cases} \frac{k\lambda^k}{x^{k+1}}, & \quad x \geq \lambda, \\ 0, & \quad x < \lambda, \end{cases} \end{align*}$

其参数 $\lambda>0, k>0$ . 对应的分布函数为

$\begin{align*} F_2(x;\lambda,k) = \begin{cases} 1-\left( \frac{\lambda}{x}\right)^k & \quad x \geq \lambda, \\ 0, & \quad x < \lambda. \end{cases} \end{align*}$

设 $(X_1,X_2)$ 的 copula 函数为

$\begin{align*} C(u,v)=uv[1+(1-u)(1-v)]. \end{align*}$

由于 Pareto 分布的重尾程度主要由 $k$ 决定, 对数正态分布则主要取决于 $\sigma$ , 为了考察其变动对逼近精度的影响, 本文给定 $\mu=0, \lambda=1$ , 同时分别选取 $k=1$ 和 $k=1.5$ , $\sigma=1$ 和 $\sigma=1.5$ , 另外为了反映 $T$ 值变化造成的影响, 分别选取 $T=500$ 和 $T=1000$ . 根据设定的参数和 $T$ 值, 对 $x=500,700,900,1100,1300,1500$ , 利用 $R$ 软件, 依次计算

(1) 两个局部分布概率之和

$\begin{align*} a_1(x,T) = \sum\limits_{i=1}^{2} [F_i(x+T) - F_i(x)]; \end{align*}$

(2) 最大值落在给定区间的概率

$\begin{align*} a_2(x,T) &= P(\max(X_1,X_2) \in (x,x+T]) \nonumber\\ &= C(F_1(x+T),F_2(x+T))-C(F_1(x)-F_2(x)); \end{align*}$

(3) 部分和落在给定区间的概率

$\begin{align*} a_3(x,T) &=P(X_1+X_2\in (x,x+T]) \nonumber\\ &= \int_{0}^{1} \frac{\partial C(u,v)}{\partial u}\Big|_{{v}=F_2(x+T-F_1^{-1}(u))}\mathrm{d}u -\int_{0}^{1} \frac{\partial C(u,v)}{\partial u}\Big|_{{v}=F_2(x-F_1^{-1}(u))}\mathrm{d}u; \end{align*}$

(4) 相对误差

$\begin{align*} \delta_{i1}(x,T) = \frac{|a_i(x,T)-a_1(x,T)|}{a_1(x,T)}, i=2,3. \end{align*}$

计算结果和相对误差如表1-8所示. 为了表达简洁, 根据 $a_i, i=1,2,3$ 的数量级作了相应的调整.

表1 $\sigma=1, k=1, T=500$ 时的计算结果和相对误差

新窗口打开| 下载CSV

表2 $\sigma=1, k=1.5, T=500$ 时的计算结果和相对误差

新窗口打开| 下载CSV

表3 $\sigma=1.5, k=1, T=500$ 时的计算结果和相对误差

新窗口打开| 下载CSV

表4 $\sigma=1.5, k=1.5, T=500$ 时的计算结果和相对误差

新窗口打开| 下载CSV

表5 $\sigma=1, k=1,T=1000$ 时的计算结果和相对误差

新窗口打开| 下载CSV

表6 $\sigma=1, k=1.5,T=1000$ 时的计算结果和相对误差

新窗口打开| 下载CSV

表7 $\sigma=1.5, k=1, T=1000$ 时的计算结果和相对误差

新窗口打开| 下载CSV

表8 $\sigma=1.5, k=1.5, T=1000$ 时的计算结果和相对误差

新窗口打开| 下载CSV

数值结果表明, 本文关于最大值和部分和的局部渐近表达式整体精度较高. 最大值的相对误差不超过 $10^{-5}$ 数量级, 对于部分和, 除了表 $8$ 中 $x=500$ 的情形之外, 其相对误差也均在 $10^{-2}-10^{-4}$ 的数量级. 此外, 通过对比发现, $k$ 和 $\sigma$ 取值较小时, 精度更高. 对于给定的参数, $T$ 值的变化对精度没有实质影响. 总体而言, 本文所得结果是稳定可行的.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Embrechts

, Goldie

C M

On closure and factorization properties of subexponential and related distributions

J Aust Math Soc Ser A, 1980, 29(2): 243-256