基于 Bernstein Copula 函数的随机变量序列的 Max-Sum 局部等价式

数学物理学报 ›› 2024, Vol. 44 ›› Issue (4): 1110-1125.

• • 上一篇

基于 Bernstein Copula 函数的随机变量序列的 Max-Sum 局部等价式

明瑞星¹(),楼振瀚¹(),崔盛^2,^3,^*(),龚婵^2,³()

¹浙江工商大学统计与数学学院杭州 310018
²三峡大学理学院湖北宜昌 443002
³三峡数学研究中心湖北宜昌 443002

收稿日期:2023-12-01 修回日期:2024-04-29 出版日期:2024-08-26 发布日期:2024-07-26
通讯作者: *崔盛, E-mail: cuisheng@ctgu.edu.cn
作者简介:明瑞星, E-mail: rxming@zjgsu.edu.cn;楼振瀚, E-mail: lzh00214@163.com;龚婵, E-mail: 2556516736@qq.com
基金资助:
浙江省重点建设高校优势特色学科 (浙江工商大学统计学)、浙江工商大学“数字+” 学科建设管理项目“数据资产: 经济理论, 价值核算, 市场交易与政策创新(SZJ2022B004);浙江省统计科学研究基地项目高维情形下最小方差投资组合研究(22TJD02);宜昌市大学科学研究与应用项目(A21-3-018)

Local Max-sum Equivalence of Random Variables with Bernstein Copula

Ming Ruixing¹(),Lou Zhenhan¹(),Cui Sheng^2,^3,^*(),Gong Chan^2,³()

¹School of Statistics and Mathematics, Zhejiang Gongshang University, Hangzhou 310018
²Science College,China Three Gorges University, Hubei Yichang 443002
³Three Gorges Mathematical Research Center,China Three Gorges University, Hubei Yichang 443002

Received:2023-12-01 Revised:2024-04-29 Online:2024-08-26 Published:2024-07-26
Supported by:
Characteristic & Preponderant Discipline of Key Construction Universities in Zhejiang Province (Zhejiang Gongshang University–Statistics), the Collaborative Innovation Center of Statistical Data Engineering Technology & Application, Digital + Discipline Construction Project(SZJ2022B004);Research on Minimum Variance Portfolio of Zhejiang Statistical Science Research Base Project in High dimension(22TJD02);Scientific Research and Application Project of Universities in Yichang City(A21-3-018)

摘要/Abstract

摘要：

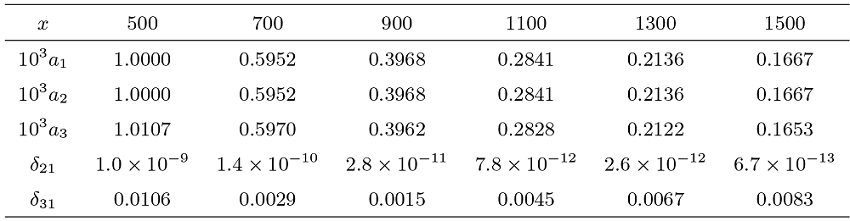
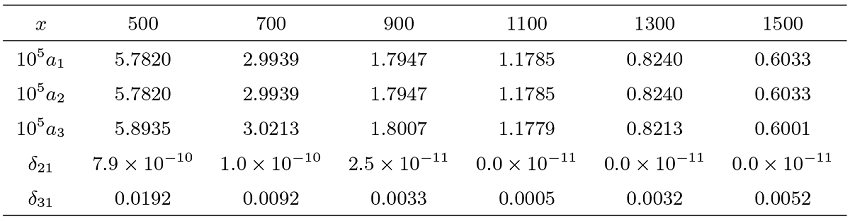
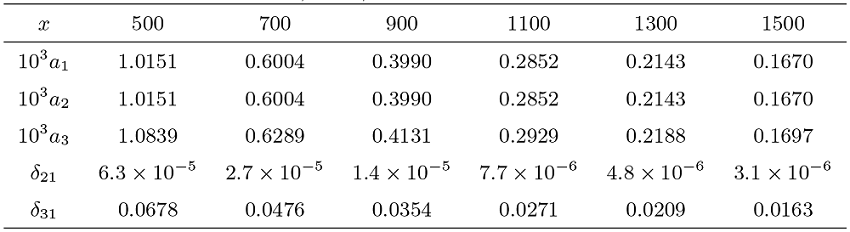
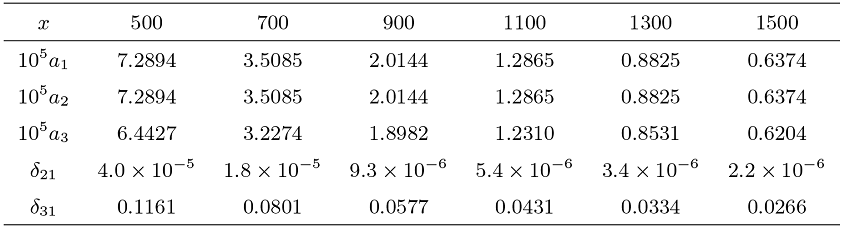
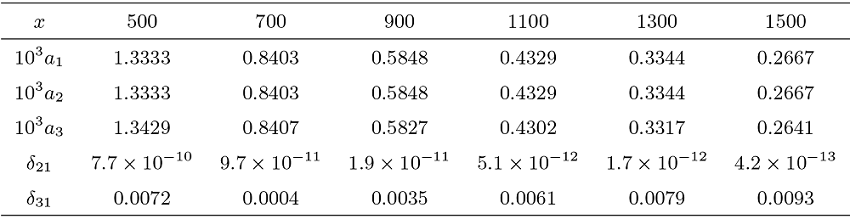
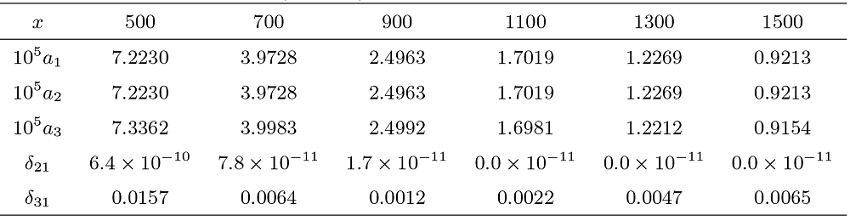
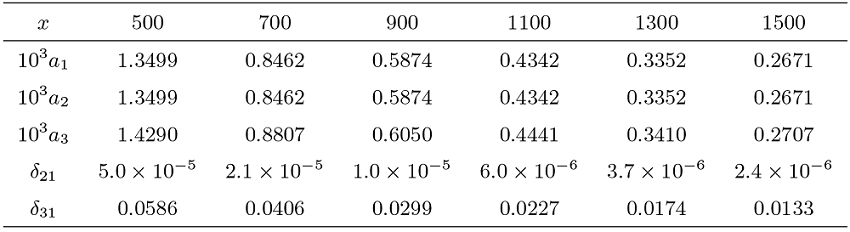
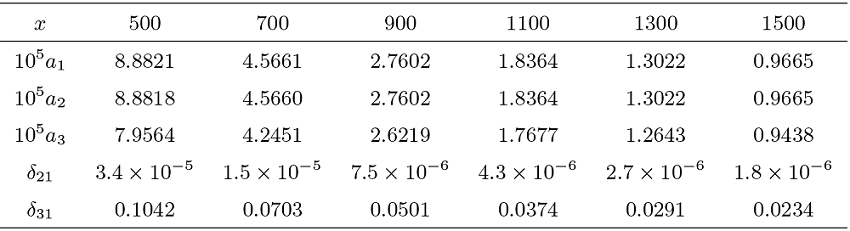
该文考虑一类具有局部长尾分布, 但不一定具有相同分布的随机变量序列, 其联合分布由 Bernstein copula 函数进行联系. 研究其部分和及其最大值的局部分布的渐近性质. 在假设诸随机变量服从局部次指数分布的条件下, 得到了 Max-Sum 局部等价性. 该等价性从局部和相依的角度描述了随机游动的一次大跳原理. 数值实验表明所得结果稳定可行.

关键词: Bernstein copula, Max-Sum 局部等价性, 局部次指数分布, 一次大跳原理

Abstract:

In this paper, we consider a sequence of non-negative dependent and not necessarily identically distributed random variables with local long-tailed marginal distributions and Bernstein copula and study the local asymptotic behavior of the tail of their partial sum and maximum. Then, under a suitable condition for local subexponentiality, we obtain the local max-sum equivalence. The result indicates that the big-jump principle of random walks remains valid in its local version under more general dependency assumptions. The numerical experimental results under different parameter settings further validate the stability and feasibility of the obtained results.

Key words: Bernstein copula, Local max-sum equivalence, Local subexponentiality, Principle of a single big jump

中图分类号:

O175.23

明瑞星, 楼振瀚, 崔盛, 龚婵. 基于 Bernstein Copula 函数的随机变量序列的 Max-Sum 局部等价式[J]. 数学物理学报, 2024, 44(4): 1110-1125.

Ming Ruixing, Lou Zhenhan, Cui Sheng, Gong Chan. Local Max-sum Equivalence of Random Variables with Bernstein Copula[J]. Acta mathematica scientia,Series A, 2024, 44(4): 1110-1125.

图/表 8

表1

表2

表3

表4

表5

表6

表7

表8

参考文献 35

[1]	Embrechts P, Goldie C M. On closure and factorization properties of subexponential and related distributions. J Aust Math Soc Ser A, 1980, 29(2): 243-256
[2]	Geluk J L, De Vries C G. Weighted sums of subexponential random variables and asymptotic dependence between returns on reinsurance equities. Insurance Math Econom, 2006, 38(1): 39-56
[3]	Wang D, Tang Q. Maxima of sums and random sums for negatively associated random variables with heavy tails. Stat Probabil Lett, 2004, 68(3): 287-295
[4]	Albrecher H, Asmussen S, Kortschak D, et al. Tail asymptotics for the sum of two heavy-tailed dependent risks. Extremes, 2006, 9(2): 107-130
[5]	Geluk J, Ng K W. Tail behavior of negatively associated heavy-tailed sums. J Appl Probab, 2006, 43(2): 587-593
[6]	Wang K, Wang Y. Notes on the asymptotics of the tail probabilities of sums for negatively associated random variables with heavy tails. Chinese J Appl Probab Stat, 2007, 23(4): 337-344
[7]	Chen Y, Yuen K C. Sums of pairwise quasi-asymptotically independent random variables with consistent variation. Stoch Models, 2009, 25(1): 76-89
[8]	Geluk J, Tang Q. Asymptotic tail probabilities of sums of dependent subexponential random variables. J Theor Probab, 2009, 22: 871-882
[9]	Foss S, Richards A. On sums of conditionally independent subexponential random variables. Math Oper Res, 2010, 35(1): 102-119
[10]	Yang Y, Wang K, Leipus R, et al. Tail behavior of sums and maxima of sums of dependent subexponential random variables. Acta Appl Math, 2011, 114(3): 219-231
[11]	Chen W, Yu C, Wang Y. Some discussions on the local distribution classes. Stat Probabil Lett, 2013, 83(7): 1654-1661
[12]	Li J. On pairwise quasi-asymptotically independent random variables and their applications. Stat Probabil Lett, 2013, 83(9): 2081-2087
[13]	Foss S, Korshunov D, Zachary S. An Introduction to Heavy-Tailed and Subexponential Distributions. New York: Springer, 2013
[14]	Asmussen S, Foss S, Korshunov D. Asymptotics for sums of random variables with local subexponential behaviour. J Theor Probab, 2003, 16(2): 489-518
[15]	Ng K, Tang Q. Asymptotic behavior of tail and local probabilities for sums of subexponential random variables. J Appl Probab, 2004, 41(1): 108-116
[16]	Denisov D, Shneer V. Local asymptotics of the cycle maximum of a heavy-tailed random walk. Adv Appl Probab, 2007, 39(1): 221-244
[17]	Denisov D, Dieker A B, Shneer V. Large deviations for random walks under subexponentiality: The big-jump domain. Ann Probab, 2008, 36(5): 1946-1991
[18]	Cui Z, Wang Y, Wang K. Asymptotics for the moments of the overshoot and undershoot of a random walk. Adv Appl Probab, 2009, 41(2): 469-494
[19]	Yang Y, Leipus R, Siaulys J. Local precise large deviations for sums of random variables with O-regularly varying densities. Stat Probabil Lett, 2010, 80(19/20): 1559-1567
[20]	刘希军, 王岳宝. 不同分布的卷积的局部封闭性及局部渐近性的充分条件和必要条件. 系统科学与数学, 2009, 29(4): 527-535 doi: 10.12341/jssms08391
	Liu X J, Wang Y B. The sufficient condition and necessary condition of local closure and local asymptotic for the convolutions of non-identical distributions. J Syst Sci Math Sci, 2009, 29(4): 527-535 doi: 10.12341/jssms08391
[21]	江涛, 徐晖. Farlie-Gumbel-Morgenstern 联合分布的 Max-Sum 局部等价式. 中国科学: 数学, 2016, 46(1): 67-80
	Jiang T, Xu H. Max-Sum local equivalence of random variables with Farlie-Gumbel-Morgenstern joint distribution. Sci Sin Math, 2016, 46(1): 67-80
[22]	柳福祥, 龚婵, 崔盛. 服从 FGM Copula 的实值重尾随机游动的局部 Max-Sum 等价. 江西师范大学学报 (自然科学版), 2020, 44(6): 609-613
	Liu F X, Gong C, Cui S. The local max-sum equivalence of real valued random walks with heavy-tailed increments following FGM copula. Journal of Jiangxi Normal University, 2020, 44(6): 609-613
[23]	Nelsen R B. An Introduction to Copulas. New York: Springer, 2006
[24]	Sancetta A, Satchell S. The Bernstein copula and its applications to modeling and approximations of multivariate distributions. Economet Theor, 2004, 20(3): 535-562
[25]	Bouezmarni T, Rombouts J V K, Taamouti A. Asymptotic properties of the Bernstein density copula estimator for $\alpha$-mixing data. J Multivariate Anal, 2010, 101(1): 1-10
[26]	Janssen P, Swanepoel J, Veraverbeke N. Large sample behavior of the Bernstein copula estimator. J Stat Plan Infer, 2012, 142(5): 1189-1197
[27]	Swanepoel J W H, Allison J S. Some new results on the empirical copula estimator with applications. Stat Probabil Lett, 2013, 83(7): 1731-1739
[28]	Tavin B. Application of Bernstein copulas to the pricing of multi-asset derivatives//Jaworski P, Durante F, Hardle W. Copulae in Mathematical and Quantitative Finance. Berlin: Springer, 2013: 277-288
[29]	Hernández-Maldonado V, Díazviera M, Erdely A. A joint stochastic simulation method using the Bernstein copula as a flexible tool for modeling nonlinear dependence structures between petrophysical properties. J Petrol Sci Eng, 2012, 90-91: 112-123
[30]	Hernández-Maldonado V, Díazviera M, Erdely A. A multivariate Bernstein copula model for permeability stochastic simulation. Geofis Int, 2014, 53(2): 163-181
[31]	Diers D, Eling M, Marek S D. Dependence modeling in non-life insurance using the Bernstein copula. Insurance Math Econom, 2012, 50(3): 430-436
[32]	镇磊, 尹留志, 方兆本. 多项式 Copula 方法对市场相关结构的分析. 中国管理科学, 2008, 16(3): 1-7
	Zhen L, Yin L Z, Fang Z B. An analysis to dependence patterns in a polynomial copula approach. Chinese J Manag Sci, 2008, 16(3): 1-7
[33]	龚婵. 相依重尾随机变量序列 Max-Sum 等价的相关研究. 宜昌: 三峡大学, 2021
	Gong C. Local Max-Sum equivalence of sequences of dependent heavy-tailed random variables. Yichang: China Three Gorges University, 2021
[34]	Coqueret G. Second order risk aggregation with the Bernstein copula. Insurance Math Econom, 2014, 58: 150-158
[35]	江涛, 明瑞星, 崔盛. 相依重尾风险模型的渐近分析. 北京: 科学出版社, 2019
	Jiang T, Ming R X, Cui S. Asymptotic Analysis of Dependent Risk Model with Heavy Tails. Beijing: Science Press, 2019

基于 Bernstein Copula 函数的随机变量序列的 Max-Sum 局部等价式

Local Max-sum Equivalence of Random Variables with Bernstein Copula

RichHTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 8

参考文献 35

相关文章 15

Metrics

本文评价

推荐阅读 10

[1]	喻婷, 冬英. 三维 Keller-Segel-Stokes 系统的快速信号扩散极限的收敛速率[J]. 数学物理学报, 2024, 44(4): 925-945.
[2]	徐瑞, 周凯娟, 白宁. 一类基于游离病毒感染和细胞-细胞传播的宿主体内 HIV-1 感染动力学模型[J]. 数学物理学报, 2024, 44(3): 771-782.
[3]	刘敬华, 李林. 迭代函数方程的同胚解[J]. 数学物理学报, 2024, 44(2): 313-325.
[4]	杨招弟, 贺衎, 段周波. 基于向量楔积的两体量子系统的纠缠度量[J]. 数学物理学报, 2024, 44(1): 246-256.
[5]	吴鹏, 何泽荣. 具有非局部感染和周期治疗的HIV感染模型的时空动力学分析[J]. 数学物理学报, 2024, 44(1): 209-226.
[6]	简慧, 龚敏, 王莉. 带部分调和势的非齐次非线性 Schrödinger 方程的爆破解[J]. 数学物理学报, 2023, 43(5): 1350-1372.
[7]	李易娴,张正杰. 一类与 Klein-Gordon-Maxwell 问题有关的方程组的基态解的存在性[J]. 数学物理学报, 2023, 43(3): 680-690.
[8]	王娟,赵杰. 振荡Robin混合边值齐次化问题[J]. 数学物理学报, 2021, 41(1): 81-90.
[9]	王娟,赵杰. 高阶方程混合边界齐次化问题[J]. 数学物理学报, 2020, 40(4): 925-933.
[10]	王跃,索洪敏,韦维. 无边界约束的一类新Kirchhoff型问题的古典解[J]. 数学物理学报, 2020, 40(4): 857-868.
[11]	梁文翠,张正杰. Kirchhoff型方程有关的非线性方程多解的存在性[J]. 数学物理学报, 2020, 40(4): 842-849.
[12]	王娟,赵杰. Neumann边值齐次化问题:W^{1, p}强收敛估计[J]. 数学物理学报, 2019, 39(5): 1115-1124.
[13]	范英飞, 章国鹏, 江欣国, 马剑. 一类二阶中立随机偏微分方程的吸引集和拟不变集[J]. 数学物理学报, 2018, 38(6): 1135-1143.
[14]	赵继红. 三维耗散型电流体动力学系统弱解的正则性准则[J]. 数学物理学报, 2018, 38(3): 549-564.
[15]	佟玉霞, 郑神州, 程林娜. 弱A-调和张量的奇点可去性[J]. 数学物理学报, 2017, 37(6): 1001-1011.