设 $ \mathbb{R}^{p} $ 和 $ \mathbb{R}^{q} $ 是有限维欧式空间, 并且每个空间上的內积和诱导范数分别表示为 $ \langle \cdot,\cdot \rangle $ 和 $ \|\cdot\|=\sqrt{\langle \cdot,\cdot \rangle}. $ 假设 $ h:\mathbb{R}^{q}\rightarrow \mathbb{R} $ 是凸函数, $ f:\mathbb{R}^{p}\rightarrow \mathbb{R}\cup\{+\infty\} $ 和 $ g:\mathbb{R}^{q}\rightarrow \mathbb{R}\cup\{+\infty\} $ 是扩展实值下半连续凸函数, $ \Phi :\mathbb{R}^{q} \times \mathbb{R}^{p} \rightarrow \mathbb{R} $ 是连续可微函数, $ K:\mathbb{R}^{q} \rightarrow \mathbb{R}^{p} $ 是有界线性算子. 函数 $ f $ 的共轭函数定义为 $ f^*(y)=\sup\limits_{x\in\mathbb{R}^{p}}\{\langle{y,x}\rangle-f(x)\} $.

考虑如下带有双线性耦合项的鞍点问题

问题 (1.1) 在许多领域有着广泛的应用, 比如信号与图像处理、压缩感知、机器学习、博弈论等, 许多学者研究了问题 (1.1), 详情见文献 [1⇓-3]. 求解问题 (1.1) 的相关算法已经有很多, 其中最经典的是 Arrow-Hurwicz 方法^[4], 即原始对偶算法. 从初始点 $ (x_{0},y_{0})\in \mathbb{R}^{q}\times \mathbb{R}^{p} $ 开始, 具体迭代为

其中 $ \tau>0, \sigma>0 $ 是步长参数. 该方法在图像处理中也被称作原始对偶混合梯度算法. 若 $ f^{*} $ 的定义域有界且步长很小时, 可基于原始对偶间隙函数得到 $ O(\frac{1}{N}) $ 的遍历收敛率, 具体的收敛性分析^[2,5]. 但是 Arrow-Hurwicz 方法在一般情况下不收敛^[6]. 为了克服这一缺点, 许多学者提出了不同的改进方法^[7⇓⇓-10].

受文献 [9] 的启发, 周丹青等^[11] 提出了一类黄金比率原始对偶算法求解如下鞍点问题

这里 $ h $ 是可微函数. 具体迭代为

其中 $ \tau, \sigma>0 $. 若 $ \tau(\sigma\|K\|^{2}+2L_{h})\leq\psi $, $ \psi\in(1,\phi] $ ($ \phi $ 是黄金比率), 周丹青等证明了算法 (1.3) 的收敛性以及 $ O(\frac{1}{N}) $ 遍历收敛率.

注意到, 在问题 (1.1) 和 (1.2) 中涉及到一个双线性函数, 但是在实际应用中许多函数往往不满足双线性性. 因此, 如何研究带非线性二元函数的鞍点问题显得尤为重要. 最近, Zhu 等^[12] 考虑了如下鞍点问题

这里 $ h $ 是可微函数. Zhu 等^[12] 提出了如下原始对偶算法

其中 $ \rho_{n-1} > 0, \eta_{n-1} = \frac{\rho_{n-1}}{2} $, $ L_{n-1} = L_{11} + L_{h} + L_{21}^{2}(2+\rho_{n-1}L_{22})\rho_{n-1} $ ( $ L_{11} $、 $ L_{21} $ 和 $ L_{22} $ 是各个 Lipschitz 常数, 见假设 2.2). 在函数 $ \nabla_{x}\Phi(x,y) $ 和 $ \nabla_{y}\Phi(x,y) $ 关于 $ x $ 和 $ y $ 是 Lipschitz 连续的假设下证明了算法 (1.5) 的收敛性以及 $ O(\frac{1}{N}) $ 遍历收敛率. 值得注意的是, 算法 (1.5) 对于邻近算子参数 $ L_{n} $ 的取值范围严重依赖于 Lipschitz 常数, 且单次循环迭代步骤较多, 这将严重影响算法的收敛速度. 此外, 函数 $ h $ 可微这一假设比较强. 事实上, 许多函数并不满足可微性. 因此, 如何在不可微情况下提出加速的算法求解问题 (1.4) 是本文讨论的重点.

本文受到文献 [11,12] 的启发, 我们提出了求解问题 (1.4) 的黄金比率原始对偶算法, 证明了由算法产生的序列收敛到问题 (1.4) 的解, 并用数值实验验证了算法的优势. 本文所得的结果改进和推广了文献 [11,12] 中相应结果.

全文用 $ \mathbb{N} $ 表示正整数集, 用 $ \phi $ 表示黄金比率, 即 $ \phi=\frac{1+\sqrt{5}}{2} $. 设 $ w:\mathbb{R}^{q}\rightarrow \mathbb{R}\bigcup \{+\infty\} $ 为扩展实值下半连续凸函数, 其有效域记为 dom$(w):=\{x\in \mathbb{R}^{q}:w(x)<+\infty\} $. 设 $ x\in \mathbb{R}^{q} $, $ w $ 在点 $ x $ 的次微分记为 $ \partial w(x) $, 即 $ \partial w(x):=\{\xi \in \mathbb{R}^{q}:w(y)\geq w(x)+\langle\xi,y-x\rangle, \forall y\in \mathbb{R}^{q}\} $, $ w $ 在点 $ x $ 的邻近点映射定义为

问题 (1.4) 的原始问题与对偶问题分别为

为了证明本文的主要结果, 我们需要如下假设.

假设 2.1 对于问题 (1.4), 设存在 $ (\bar{x},\bar{y})\in ({\rm dom}(h)\cap {\rm dom}(g))\times {\rm dom}(f) $ 使得

并且 $ ({\rm dom}(h)\cap {\rm dom}(g))\times {\rm dom}(f)\subseteq {\rm dom}(\Phi) $ 以及 $ \mathcal{L}(\bar{x},\bar{y}) $ 是有界的.

注 2.1 假设 2.1 是凸凹极小极大问题中的标准假设. 它保证了强对偶性 $ (P^{*}=D^{*}=\mathcal{L}(\bar{x},\bar{y})) $ 以及问题 $ P^{*} $、 $ D^{*} $ 解的存在性^[14].

假设 2.2 对任意的 $ y\in {\rm dom}(f) $, $ x\in {\rm dom}(g)\cap {\rm dom}(h) $, $ \Phi(x,y) $ 关于 $ x $ 和 $ y $ 分别是凸函数和凹函数. 此外, 对任意的 $ x_{1}, x_{2}\in {\rm dom}(g)\cap {\rm dom}(h) $ 和 $ y_{1}, y_{2}\in {\rm dom}(f) $ 满足

注 2.2 假设 2.2 广泛用于求解凸凹极小极大问题^[12,13], 即要求 $ \nabla_{x}\Phi(x,y) $ 和 $ \nabla_{y}\Phi(x,y) $ 关于 $ x $ 和 $ y $ 是 Lipschitz 连续的.

假设 2.3 对任意的 $ u_{n}\in \partial h(x_{n}) $, $ u_{n-1}\in \partial h(x_{n-1}) $, 存在 $ L_{h}>0 $ 满足

注 2.3 若 $ h $ 是可微的, 则假设 2.3 退化为文献 [11,12] 中的梯度 Lipschitz 连续性假设.

由假设 2.1 知问题 (1.4) 的鞍点集非空, 并记为

引理 2.1^[1] 设 $ w:\mathbb{R}^{q}\rightarrow \mathbb{R}\bigcup \{+\infty\} $ 是扩展实值闭正常凸函数, $ \lambda>0 $ 以及 $ x\in \mathbb{R}^{q} $, 则

引理 2.2^[14] 设 $ \{a_{n}\}_{n\in \mathbb{N}} $ 和 $ \{b_{n}\}_{n\in \mathbb{N}} $ 是非负实数列. 如果存在 $ N>0 $ 使得 $ a_{n+1}\leq a_{n}-b_{n} $, $ \forall n\geq N $, 那么 $ \lim\limits_{n\rightarrow\infty}a_{n} $ 存在且 $ \lim\limits_{n\rightarrow\infty}b_{n}=0 $.

引理 2.3^[14] 对任意 $ x,y,z\in \mathbb{R}^{q} $ 和 $ \alpha \in \mathbb{R} $ 有

设 $ (\bar{x},\bar{y}) $ 是问题 (1.4) 的解, 则

取 $ \bar{u} \in \partial h(\bar{x}) $, 则上式等价于

故问题 (1.4) 的原始对偶间隙函数定义为

显然, $ P(x),D(y) $ 和 $ G(x,y) $ 都是凸函数且 $ G(x,y)\geq0. $ 对任意的 $ y\in {\rm dom}(f) $, $ x\in {\rm dom}(g)\cap {\rm dom}(h) $, $ G(x^{*},y^{*}) = 0 $ 当且仅当 $ (x^{*},y^{*}) $ 是问题 (1.4) 的鞍点.

本文提出如下算法

注 3.1 当 $ \Phi(x,y) = \langle Kx,y \rangle $ 且 $ h $ 是可微函数时, 算法 1 就退化为文献 [11,算法 1].

注 3.2 算法 1 是完全可分裂的, 即在每次迭代中不依赖于求解任何子问题或线性方程组. 而且算法1 完全不同于文献 [12,算法 1] 的变体 1 (记为 Alg.1(v1)), 本文的算法更加的简洁, 数值效果更好, 见数值实验部分.

为了证明收敛性结果, 我们首先证明如下引理.

引理 3.1 假设 $ \{(x_{n},y_{n},z_{n})\}_{n\in \mathbb{N}} $ 是由算法 1 产生的序列, $ (\bar{x},\bar{y})\in S $ 以及 $ \bar{u} \in \partial h(\bar{x}) $, 那么对于任意的 $ (x,y) \in \mathbb{R}^{q}\times \mathbb{R}^{p} $, 有

证 由引理 2.1 可得

由 $ G(x,y) $ 的定义知

上式结合 (3.2) 式有

又因为 $ x_{n}-z_{n}=\psi(x_{n}-z_{n+1}) $, 以及函数 $ \Phi(\cdot,\cdot) $ 关于第一变元的凸性和关于第二变元的凹性, 有

由于 $ h $ 是凸函数, 则次梯度算子是单调的. 故 $ \langle u_{n}- \bar{u},x_{n}-\bar{x}\rangle \geq 0 $. 因此 (3.1) 式成立. 证毕.

下面给出算法的收敛性证明.

定理 3.1 假设 $ \{(x_{n},y_{n},z_{n})\}_{n\in \mathbb{N}} $ 是由算法 1 产生的序列, $ (\bar{x},\bar{y})\in S $ 以及 $ \bar{u} \in \partial h(\bar{x}) $. 则 $ \{(x_{n},y_{n})\}_{n\in \mathbb{N}} $ 收敛到问题 (1.4) 的解, 即收敛到 $ S $ 中的一个元素.

证 由引理 2.3, 引理 3.1, 假设 2.2 和 Cauchy-Schwarz 不等式得

注意到 $ x_{n+1}=\frac{\psi}{\psi-1}z_{n+2}-\frac{1}{\psi-1}z_{n+1} $ 和 $ z_{n+2}-z_{n+1}=\frac{\psi-1}{\psi}(x_{n+1}-z_{n+1}) $. 由引理 2.3 可得

由于

则由 (3.3) 和 (3.4) 式可得

因为 $ \tau(2L_{h}+2L_{11}+L_{12})\leq \psi, \psi \in (1,\phi] $ 且 $ L_{12}+2L_{21}\leq \frac{1}{\sigma} $, 则 $ \psi-\tau L_{h}-\tau L_{11}-\tau L_{12}\geq\tau L_{h}+\tau L_{11} $ 以及 $ \frac{\tau}{\sigma}-\tau L_{12}-2\tau L_{21}\geq0 $. 又因为 $ \psi\leq\phi $, 故 $ \psi-1-\frac{1}{\psi}\leq0 $. 因此上式可简化为

令

注意到 $ G(x_{n},y_{n})\geq 0 $, 则

显然 $ a_{n}\geq0 $, $ b_{n}\geq 0 $. 由引理 2.2 知 $ \lim\limits_{n\rightarrow\infty}a_{n} $ 存在以及 $ \lim\limits_{n\rightarrow\infty}b_{n}=0 $. 又由 $ x_{n}-z_{n}=\psi(x_{n}-z_{n+1}) $ 以及 $ b_{n} $ 的定义可知

因为 $ \lim\limits_{n\rightarrow\infty}a_{n} $ 存在, 故 $ \{z_{n+1}\}_{n\in \mathbb{N}} $ 和 $ \{y_{n}\}_{n\in \mathbb{N}} $ 是有界的. 进一步有 $ \{(z_{n+1},y_{n})\}_{n\in \mathbb{N}} $ 有界. 又因为 $ \lim\limits_{n\rightarrow\infty}\|z_{n}-x_{n}\|=0 $, 所以 $ \{x_{n}\}_{n\in \mathbb{N}} $ 也有界.

下面证明 $ \{(x_{n},y_{n})\}_{n\in \mathbb{N}} $ 收敛到问题 (1.4) 的一个解. 不妨假设 $ \{(x_{n+1},y_{n})\}_{n\in \mathbb{N}} $ 的子列 $ \{(x_{n_{k}+1},y_{n_{k}})\}_{k\in \mathbb{N}} $ 收敛于 $ (x^{*},y^{*}) $. 则 $ \lim\limits_{k\rightarrow\infty}x_{n_{k}}=\lim\limits_{k\rightarrow\infty}x_{n_{k}+1}=x^{*}, \lim\limits_{k\rightarrow\infty}y_{n_{k}}=\lim\limits_{k\rightarrow\infty}y_{n_{k}-1}=y^{*} $. 对任意的 $ (x,y)\in \mathbb{R}^{q}\times \mathbb{R}^{p} $, 选取 $ u_{n_{k}} \in \partial h(x_{n_{k}}) $, 由引理 2.1 得如下不等式组

由于 $ g $, $ f^{*} $ 是下半连续的, 则在上式中令 $ k\rightarrow \infty $ 且两边同时除以 $ \tau(\tau>0) $, 选取 $ u^{*} \in \partial h(x^{*}) $ 得

因此 $ (x^{*},y^{*})\in S $. 同时对任意的 $ (\bar{x},\bar{y})\in S $, 以上证明仍然成立. 因此, 在 (3.5) 式中可用 $ (x^{*},y^{*}) $ 去代替 $ (\bar{x},\bar{y}) $, 得到

由此可得 $ \lim\limits_{k\rightarrow\infty}a_{n_{k}}=0 $. 又因为 $ \{a_{n}\}_{n\in \mathbb{N}} $ 单调不增, 故 $ \lim\limits_{n\rightarrow\infty}a_{n}=0 $. 因此 $ \lim\limits_{n\rightarrow\infty}x_{n}=\lim\limits_{n\rightarrow\infty}z_{n+1}=x^{*} $ 且 $\lim _{n \rightarrow \infty} y_{n}=y^{*}$. 证毕.

下面给出算法 1 的 $ O(\frac{1}{N}) $ 遍历收敛速率.

定理 3.2 假设 $ \{(x_{n},y_{n},z_{n})\}_{n\in \mathbb{N}} $ 是由算法 1 产生的序列, $ (\bar{x},\bar{y})\in S $ 以及 $ \bar{u} \in \partial h(\bar{x}) $. 设 $ N\geq 1 $ 是任意正整数, 正整数 $ t $ 是满足 $ 0<t<N $, 并定义

则

证 由 (3.5) 和 (3.6) 式知, 对任意的 $ n\geq 1 $, 有 $ 2\tau G(x_{n},y_{n})\leq a_{n}-a_{n+1} $. 从 $ n=t,\cdots,N $, 将以上不等式相加, 得 $ 2\tau \sum\limits_{n=t}^{N}G(x_{n},y_{n})\leq a_{t}-a_{N+1}\leq a_{t} $. 注意到, $ G(x,y)=P(x)+D(y) $ 且 $ P(x) $ 和 $ D(y) $ 是凸函数, 由 Jessen 不等式和 (3.7) 式得

上式联合 $ a_{t}=\frac{\psi}{\psi-1}\|z_{t+1}-\bar{x}\|^{2}+\frac{\tau}{\sigma}\|y_{t-1}-\bar{y}\|^{2}+\tau (L_{h}+ L_{11})\|x_{t}-x_{t-1}\|^{2} $ 可得结论. 证毕.

注 3.3 定理 3.1 从以下两个方面改进了文献 [12,定理 2]

(i) 将 $ h $ 的可微性弱化到不可微.

(ii) 本文提出的算法完全不同于文献 [12,算法 1] 的变体 1, 在算法的形式上更为精简. 算法 1 采用了黄金比率凸组合技术, 这可以显著的减少算法的迭代次数与运行时间, 见数值实验部分.

注 3.4 当 $ \Phi(x,y) = \langle Kx,y \rangle $ 且 $ h $ 是可微函数时, 由本文定理 3.1 和 3.2, 我们可以重新获得文献 [11,定理 3.1 和 3.2].

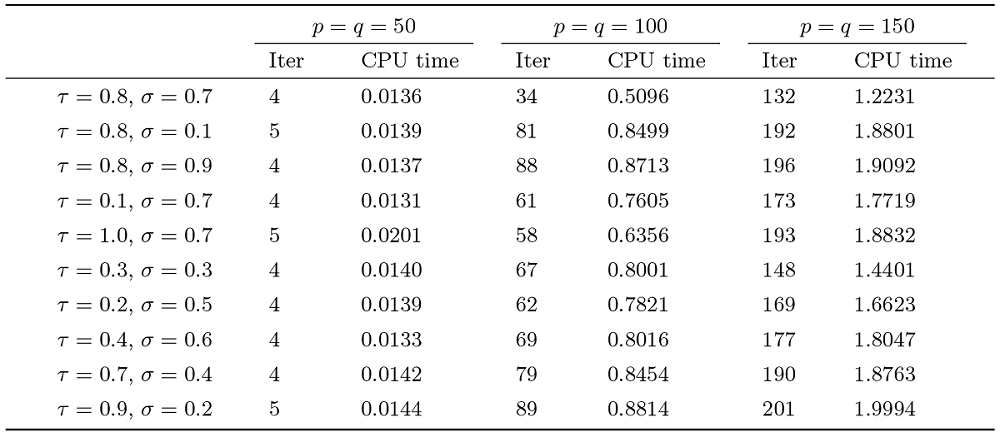
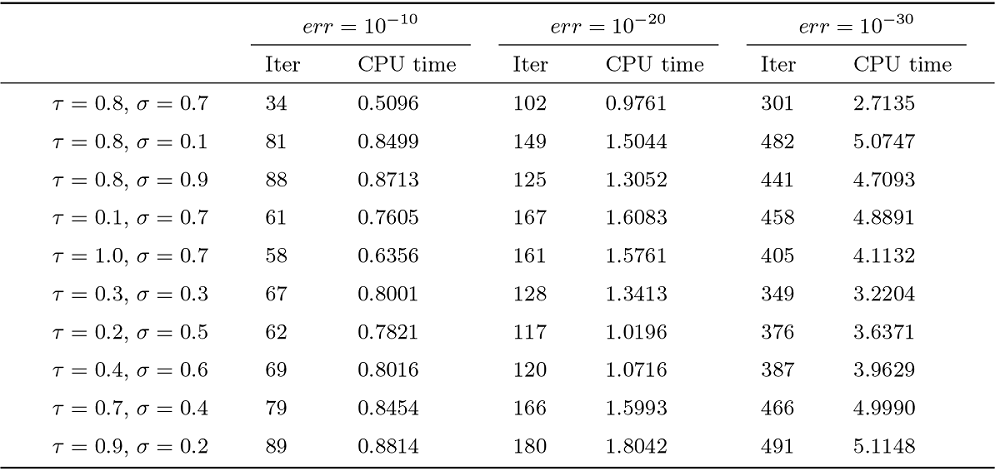
本节给出数值实验, 通过两个例子将本文算法 1 与文献 [12,算法 1] 的变体 1 (记为 Alg.1(v1)) 进行比较. 所有代码均在 MATLAB R2018a 和 Windows10 系统下运行, 计算机基本参数为 Intel(R) Core(TM) i5-8250U CPU@1.60GHz, 其中 “iter” 表示程序迭代次数, “CPU time” 表示程序运行时间, 单位为秒. 算法的终止条件为 $ ||[x_{n};y_{n}] - [x_{n-1};y_{n-1}]||^{2}\leq err$ (err 为提前设定的误差).

例 4.1^[12] 考虑如下二次规划问题

其中 $ A_{i}\in \mathbb{R}^{q\times q} $ 是对称半正定矩阵, $ b_{i}\in \mathbb{R}^{q} $, $ c_{i}\in \mathbb{R}.$$ A_{0} $ 是正定矩阵, $ D:=10 $. 显然, (4.1) 式可转化为问题 (1.4), 其中 $ X:=\{x\in \mathbb{R}^{q}:\|x\| \leq D\} $, $ g(x):=\delta_{X}(x) $, $ f^{*}(y):=\delta_{\mathbb{R}^{p}_{+}}(y) $, $ \Phi(x,y):=\Sigma^{p}_{i=1}y_{i}w_{i}(x) $, $ w_{i}(x):=\frac{1}{2}x^{T}A_{i}x+b_{i}^{T}x+c_{i} $. 设初始点 $ x_{0}=y_{0}=(0,0,\cdots 0)^{T} $, $ A_{0} $, $ A_{i} $, $ b_{0} $, $ b_{i} $, $ c_{i} $ 分别是服从正态分布的随机矩阵、随机向量、随机数. 在此情况下, 我们对比了两种算法在不同维数 $ p $, $ q $ 和不同误差情况下的数值效果. 见表1和表2.

参数选取如下

算法 1 设 $ \tau=0.1, \sigma=0.1, \psi=1.6. $

文献 [12,算法 1] 的变体 1: 设 $ \rho=0.8, \eta=\frac{\rho}{2}, L_{11}=10, L_{f}=10, L_{21}=20, L_{22}=20 $.

例 4.2 考虑下述极大极小博弈问题

其中 $ \Delta_{q}:=\{x\in \mathbb{R}^{q}_{+}:\Sigma^{q}_{j=1}x_{j}=1\} $, $ \Delta_{p}:=\{y\in \mathbb{R}^{p}_{+}:\Sigma^{p}_{i=1}y_{i}=1\} $. 显然, (4.2) 式可转化为问题 (1.4), $ g(x):=\delta_{\Delta_{q}}(x), f^{*}(y):=\delta_{\Delta_{p}}(y) $, $ h(x):=\frac{1}{N}\sum\limits^{N}_{j=1}\log(1+\exp(a_{j}^{T}x)) $, $ \Phi(x,y):=\langle j(x),k(y)\rangle $, $ j_{i}(x):=\frac{b_{i}}{1+x_{i}} $, $ k_{i}(y):=y_{i} $. 设初始点 $ x_{0}=y_{0}=(0,0,\cdots 0)^{T} $, $ a_{j} $ 是服从正态分布的随机向量. 在此情况下, 我们对比了两种算法在不同维数 $ p $, $ q $ 和不同误差情况下的数值效果. 见表3和表4.

参数选取如下

算法 1 设 $ \tau$=0.8, $\sigma$=0.8, $\psi$=1.2.

文献 [12,算法 1] 的变体 1 设 $ \rho=1.4, \eta=\frac{\rho}{2}, L_{11}=10, L_{f}=10, L_{21}=20, L_{22}=20 $.

例 4.3 考虑下述极大极小问题

其中 $ \Delta_{q}:=\{x\in \mathbb{R}^{q}_{+}:\Sigma^{q}_{j=1}x_{j}=1\} $, $ \Delta_{p}:=\{y\in \mathbb{R}^{p}_{+}:\Sigma^{p}_{i=1}y_{i}=1\} $. 显然, (4.3) 式可转化为问题 (1.4), $ g(x):=\delta_{\Delta_{q}}(x), f^{*}(y):=\delta_{\Delta_{p}}(y) $, $ h(x):=\|x\|_{1} $, $ \Phi(x,y):=\langle j(x),k(y)\rangle $, $ j_{i}(x):=\frac{b_{i}}{1+x_{i}} $, $ k_{i}(y):=y_{i} $. 设初始点 $ x_{0}=y_{0}=(1,1,\cdots 1)^{T} $, $ a_{j} $ 是服从正态分布的随机向量. 由于 $ h $ 是非光滑函数, 所以文献 [12,算法 1] 的变体 1 以及文献 [11,算法 1] 不能求解本例子. 取 $ \psi=1.2 $, 在不可微点 $ x_{n-1}^{i}=0 (x_{n-1} $ 的第 $ i $ 个分量), 取次梯度 $ u_{n-1}^{i} = 0 \in \partial h(x_{n-1}^{i}) $. 在此情况下, 我们对比了算法 1 在不同维数 $ p $, $ q $, 不同步长和不同误差情况下的数值效果. 见表5、表6. 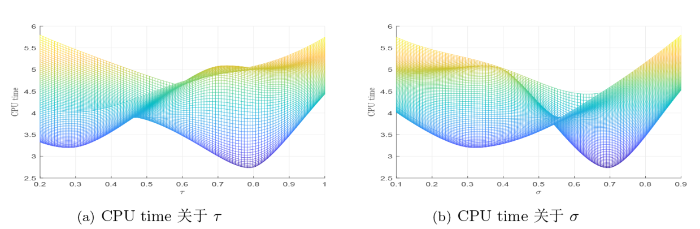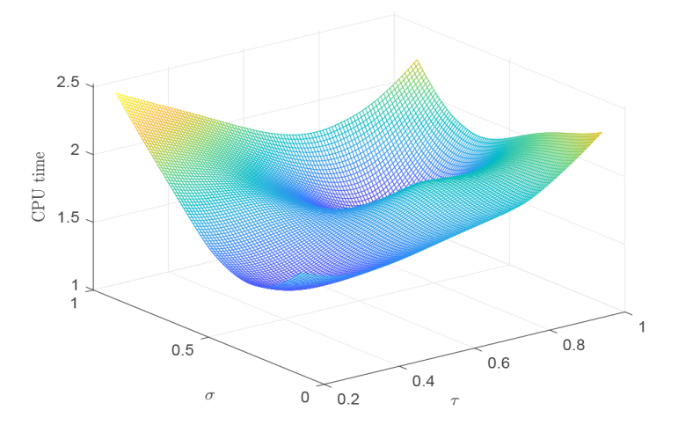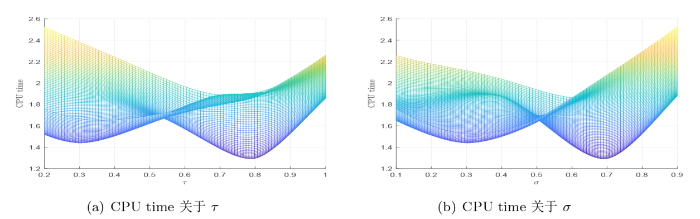更进一步, 我们在 $ p=q=150 $ 以及 $ err=10^{-30} $ 两种情况下分别给出了CPU time关于步长 ($ \tau, \sigma $) 的三维曲面图以及剖面图, 见图1、图2、图3、图4.

注 4.1 从数值实验的结果来看, 我们有

(i) 算法 1 与文献 [12,算法 1] 的变体 1 都收敛到问题的解.

(ii) 从 CPU 运行时间来看 (针对例 4.1 与例 4.2), 在适当参数的选取下, 算法 1 优于文献 [12,算法 1], 见表1-4.

(iii) 从迭代次数来看, 在适当参数的选取下, 例 4.2 中算法 1 随着维度和精度的增加仍然表现出很强的稳定性, 较文献 [12,算法 1] 的变体 1 数值效果更佳, 见表3和表4.

(iv) 例 4.3 中, 在 $ err=10^{-10} $, $ p=q=50 $, $ p=q=100 $, $ p=q=150 $ 的情况下, 我们选取了多组步长, 得到 $ \tau=0.8 $, $ \sigma=0.7 $ 时的数值效果最佳, 见表5及图1, 图2; 以及在 $ p=q=100 $, $ err=10^{-10} $, $ err=10^{-20} $, $ err=10^{-30} $ 的情况下, 我们选取了多组步长, 同样得到 $ \tau=0.8 $, $ \sigma=0.7 $ 时的数值效果最佳, 见表6及图3, 图4.

(v) 算法 1 在 $ h $ 光滑与非光滑的条件下同样适用.