特征提取一直是图像处理和计算机视觉研究领域中一个值得探讨的问题, 在计算机科学、医疗辅助诊断、军事、工业测量等众多领域应用广泛. 在计算机视觉和模式识别中, 如何准确定位和提取关键特征是其中首先需要解决的问题之一. 最小二乘回归是一种最简单有效的特征提取和数据降维方法. 经典的最小二乘回归方法, 即岭回归 (ridge regression, RR), 可由如下优化问题得到^[1,2]

其中 $ \operatorname{loss}(\cdot) $ 为损失函数, $ {y_i} $ 为样本 $ {x_i} $ 的标签, $ R(f) $ 为 $ f $ 上的正则化函数, $ \psi>0 $ 为正则化参数. 然而 RR 方法具有潜在的缺点, 因其使用 $ L_2 $ 范数或 Frobenius 范数作为度量, 对含有异常值的数据较敏感, 同时该方法也只能获得有限数量的投影. 为解决这一问题, 通用处理方法为在回归模型中放弃使用标记指示矩阵, 同时引用数据集函数 $ g\left(x_j\right) $, 得到如下修正的正则化回归模型

文献 [1,3,4] 都可以用上述模型进行总结. 文献 [5⇓⇓-8] 指出, 局部几何结构在低维子空间的学习中起着重要的作用, 而几何结构或类特定结构在降维中非常重要, 这些信息可以帮助我们找到有意义的低维表征, 增强表征能力. 其核心思想是先定义一个类内相似图, 然后在低维子空间中保存该图所表征的信息. 遵循这一思路, Lai^[9] 提出的 RDR(robust discriminant regression) 模型中引入类内相似图, 将局部几何结构整合进回归模型, 同时使用鲁棒范数作为主要度量, 利用正交约束回归模型得到 RDR 的如下目标函数

其中矩阵 $ W=(W_{ij}) $ 描述了数据集的局部流形结构. 假定函数 $ f $ 和 $ g $ 为线性投影算子, 基于 $ L_{2,1} $ 范数定义

文献 [9] 为增强算法鲁棒性, 通过最小化加权 $ L_{2,1} $ 范数损失函数来保持局部几何结构, 同时对正交约束的回归模型 (1.3) 进行广义扩展, 得到 RDR 模型的具体形式如下

其中 $ X=\left[x_1^T, x_2^T, \cdots, x_N^T\right]\in\!\! \mathbb{R}^{\!\!N\times m} $ 为包含所有训练样本 $ \left\{x_i\right\}_{i=1}^N \in \mathbb{R}^m $ 的数据矩阵, $ \|\cdot\|_F $ 为矩阵 Frobnius 范数. 文献 [9] 指出用 $ L_{2,1} $ 范数作为基本度量可以使得离群值的重要性低于 $ \left\|x_i-x_j Q P\right\|_2^2 $. 基于 $ L_{2,1} $ 范数相关性质^[10], 模型 (1.4) 的目标函数可转化为

其中 $ \mathrm{tr}(A) $ 表示方阵 $ A $ 的迹,

定义

和具有非负对角元的对角矩阵 $ D\in\!\! \mathbb{R}^{\!\!N\times N} $, 其中 $ \odot $ 表示矩阵 Hadamard 积, $ D $ 的对角元素定义为

模型 (1.4) 可进一步可转化为如下迹函数极小化模型

模型 (1.6) 中, 因为目标函数的复杂性且双未知变量 $ Q,P $ 互相耦合, 同时矩阵 $ F $ 和 $ D $ 依赖于变量 $ Q,P $, 故其关于无约束变量 $ P $ 和列正交约束变量 $ Q $ 没有明确的解析表达式. 文献 [9] 设计了基于近似交替最小二乘思想的求解方案: (1) 固定$ (Q,F,D) $, 更新 $ P $; (2) 固定 $ (P,F,D) $, 更新 $ Q $; (3) 更新 $ (F,D) $. 但在每次迭代中, 关于变量 $ P $ 的子问题需要利用到矩阵逆运算得到解析表达式, 增加了算法的数值不稳定性; 关于变量 $ Q $ 的子问题没有精确解析表达式, 文献 [9] 给出近似的解析表达式, 但需要计算矩阵的完整特征值分解, 这导致该算法计算复杂度较高 (具体见 5.1 节). 同时注意到交替最小二乘方法缺乏完整的全局收敛性分析, 其迭代速度和满足迭代终止条件的迭代解精度并不理想. 为更有效地求解模型 (1.6), 本文在 $ (F,D) $ 取为固定值的前提下, 对于变量 $ Q,P $ 的更新, 整合紧流形和线性流形, 从黎曼优化的角度设计基于乘积流形的黎曼一阶优化算法进行求解. 注意到变量 $ Q $ 的可行集 $ \left\{Q \in \mathbb{R}^{m \times d} \mid Q^T Q=I_d\right\} $, 通常被称为 Stiefel 流形并记为 $ \mathrm{St}(m, d) $, 是向量空间 $ \mathbb{R}^{m \times d} $ 中的一个维数为 $ m p-\frac{1}{2} d(d+1) $ 的嵌入子流形, 而向量空间$ \mathcal{P}:=\mathbb{R}^{d \times m} $ 也可视为线性流形. 若记

假定 $ F, D $ 取为固定矩阵, 模型 (1.6) 可简化为如下乘积流形约束下的矩阵优化问题

传统上在欧氏空间中处理一些具有约束的问题常使用拉格朗日法或贪婪算法, 而这些方法往往会导致次优解的生成. 为了在数值计算中获得更精确的数值解, 黎曼流形优化开辟了一个新的方向. 采用黎曼流形优化有两个显著的优势: 第一, 对于许多具有黎曼几何结构约束的优化问题, 通过黎曼流形上的优化可以更好地利用约束空间的几何结构, 转化为黎曼流形上的无约束优化问题, 以获得更精确的数值解. 第二, 通过引入适当的度量, 可以将某些欧氏空间中的非凸问题转化为黎曼流形上的凸问题, 进而改善数值计算方法, 获得全局最优解.

黎曼流形优化问题目前已广泛应用于机器学习, 数据挖掘, 计算机视觉, 材料科学等领域. 如果将可行集限制在流形上, 流形优化问题就是一个流形上的无约束优化问题. 因此只要保证迭代点在流形上, 各种无约束优化算法都对应着流形上的优化算法, 如梯度类方法, 共轭梯度法, 信赖域方法, 牛顿法, 拟牛顿法和阻尼牛顿法等. 乘积流形黎曼优化近年来也得到了国内外学者的大量关注, 并应用于实际问题获得了一系列的研究成果. 理论和实践证明, 将具有约束的多变量矩阵优化问题转化为相应乘积流形上的无约束优化问题, 引入黎曼流形优化算法可以获得更有效的数值解. 如 Sato 和 Sato^[11]提出了基于乘积流形 $ \textrm{Sym}_{+}(r) \times \mathrm{St}(n, r) \times \mathbb{R}^{m \times r} $ (其中 $ \textrm{Sym}_{+}(r) $ 为对称正定矩阵构成的流形) 上的黎曼信赖域算法研究了保结构 $ H^2 $ 最优模型缩减问题; 同时将对称线性连续时间系统的在线最优辨识问题转化为乘积流形 $ \textrm{Sym}_{+}(r) \times \mathbb{R}^{n \times m} \times \mathbb{R}^{p \times m} $ 上的矩阵优化模型, 并提出了基于乘积流形的黎曼梯度类求解算法^[12]. Sato^[13,14] 将线性稳定 port Hamiltonian 系统模型缩减问题转化为乘积流形 $ \textrm{Skew}(r) \times \textrm{Sym}_{+}(r) \times \mathbb{R}^{r \times m} $ (其中 $ \textrm{Skew}(r) $ 表示 $ {r} $ 阶反对称矩阵构成的线性流形)上的矩阵优化模型, 并分别提出了基于乘积流形的黎曼最速下降法和黎曼信赖域求解算法. Sato, Sato 和 Damm^[15]将源于电气网络系统, 多代理网络系统, 建筑物温度动态系统中的三类线性连续时间对称系统辨识问题分别转化为乘积流形 $ \textrm{Sym}_{+}(r) \times \mathbb{R}^{n \times m} \times \mathbb{R}^{p \times m} $、商流形 $ N / O(n) $、 $ \textrm{Diag}_{+}(n) \times \mathbb{R}^{n \times m} \times \mathbb{R}^{p \times m} $ (其中 $ \textrm{Diag}_{+}(n) $ 为具有正对角元对角阵构成的流形) 上的矩阵优化模型, 并提出了基于相应乘积流形上的黎曼共轭梯度类求解算法. 更多关于乘积流形黎曼优化及其应用的文献见 [16⇓⇓⇓⇓⇓⇓⇓⇓-25].

黎曼共轭梯度法是欧式空间非线性共轭梯度法在流形上的推广, 由于其良好的收敛特性, 目前已成为黎曼可行一阶优化方法中较常用的算法, 近年来各类黎曼非线性共轭梯度法得到了国内外学者的持续关注, 并应用于具体问题获得了相当丰富的研究成果^{[26⇓⇓⇓⇓⇓⇓-33]}. 本文结合乘积流形 $ \mathrm{St}(m, d) \times \mathcal{P} $ 的几何性质, 基于 Zhang-Hager 技术^[34] 拓展, 将黎曼共轭梯度法进一步推广到求解模型 (1.7) 上, 设计一类自适应问题的黎曼非线性共轭梯度法, 并给出算法全局收敛性分析. 数值实验验证所提算法对于求解问题是可行有效的, 与其他黎曼梯度算法及黎曼优化工具箱中已有的黎曼一阶和二阶算法相比在迭代效率上有一定优势.

本文余下内容组织如下: 第 2 节讨论乘积流形 $ \mathrm{St}(m, d) \times \mathcal{P} $ 的几何性质, 给出 (1.7) 中目标函数黎曼梯度和黎曼海塞的具体计算公式; 第 3 节给出求解问题 (1.7) 的黎曼非线性共轭梯度法的算法框架; 第 4 节进而给出算法全局收敛性分析; 第 5 节给出了数值实验和数值比较验证所提出的算法对于问题 (1.7) 的有效性; 最后第 6 节进行总结.

首先给出乘积流形 $ \mathrm{St}(m, d) \times \mathcal{P} $ 若干几何性质, 关于 Stiefel 流形 $ \mathrm{St}(m, d) $ 的更多性质读者可参考文献 [35]. 因为 $ \mathrm{St}(m, d) $ 的维数 $ \operatorname{dim}(\mathrm{St}(m, d))=m p-\frac{1}{2} d(d+1) $, 故有

由于 Stiefel 流形 $ \mathrm{St}(m, d) $ 在点 $ Q \in \mathrm{St}(m, d) $ 的切空间 $ \mathcal{T}_{Q} \mathrm{St}(m, d) $ 可表示为

同时线性流形 $ \mathcal{P} $ 在点 $ P \in \mathcal{P} $ 处的切空间

故乘积流形 $ \mathrm{St}(m, d) \times \mathcal{P} $ 在 $ (Q, P) \in \mathrm{St}(m, d) \times \mathcal{P} $ 处的切空间可表示为

令在欧式空间 $ \mathbb{R}^{n \times d} \times \mathbb{R}^{d \times m} $ 上有如下标准内积

由于乘积流形 $ \mathrm{St}(m, d) \times \mathcal{P} $ 是 $ \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} $ 的嵌入子流形, 故对于 $ \forall(Q, P) \in \mathrm{St}(m, d) \times \mathcal{P} $ 和 $ \left(\eta_1, \xi_1\right) $, $ \left(\eta_2, \xi_2\right) \in \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} $, 乘积流形上的黎曼度量可定义为

其诱导范数为 $ \|(\eta_1, \xi_1)\|_{(Q, P)}:=\sqrt{\|\eta_1\|_F^2+\|\xi_1\|_F^2} $. 为讨论方便, 下文分别用 $ \langle\cdot,\cdot\rangle $ 和 $ \|\cdot\| $ 表示 $ \mathrm{St}(m, d) \times \mathcal{P} $ 上的黎曼度量及其诱导范数. 在黎曼度量 (2.1) 式下, $ \forall(E,F)\in \mathbb{R}^{m \times d}\times \mathbb{R}^{d \times m} $, 其在切空间 $ \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} $ 的正交投影为

其中

分别表示 $ E $ 和 $ F $ 在切空间 $ \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) $ 和 $ \mathcal{P} $ 上的正交投影, 其中 $ \mathrm{sym}(M)=\frac{1}{2}(M+M^T) $, $ \forall M\in\!\! \mathbb{R}^{\!\!d\times d} $.

对于乘积流形 $ \mathrm{St}(m, d) \times \mathcal{P} $ 上的黎曼优化方法, 其一般迭代框架为

其中 $ \left(Q^{(k)}, P^{(k)}\right) $ 为当前迭代步, $ \alpha_k $ 为迭代步长, $ \left(\eta^{(k)}, \xi^{(k)}\right) $ 为切空间 $ \mathcal{T}_{\left(Q^{(k)}, P^{(k)}\right)} \mathrm{St}(m, d) \times \mathcal{P} $ 内的搜索方向,

表示限制在乘积流形上点 $ \left(Q^{(k)}, P^{(k)}\right) $ 对应切空间即$ \mathcal{T}_{\left(Q^{(k)}, P^{(k)}\right)} \mathrm{St}(m, d) \times \mathcal{P} $ 上的收缩算子. $ \forall \alpha \in \mathbb{R}, (Q, P) \in \mathrm{St}(m, d) \times \mathcal{P}, (\eta, \xi) \in \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} $, 乘积流形 $ \mathrm{St}(m, d) \times \mathcal{P} $ 上的收缩算子定义为

其中, $ \mathcal{R}_P(\alpha \xi)=P+\alpha \xi$ 为定义在线性流形 $ \mathcal{P} $ 上的收缩算子, $ \mathcal{R}_Q(\alpha \eta) $ 为 Stiefel 流形 $ \mathrm{St}(m, d) $ 上的收缩算子. 对于 Stiefel 流形 $ \mathrm{St}(m, d) $, 目前常用的收缩算子有基于指数映射, $ QR $ 分解, 极分解, 流形投影, Cayley 变换等. 本文采用基于 $ QR $ 分解的收缩算子, 其具体计算公式为

其中对于给定的列满秩矩阵 $ A \in \mathbb{R}^{m \times d} $, $ \mathrm{qf}(A)\in\!\! \mathbb{R}^{\!\!m \times d} $ 表示 $ A $ 的简洁版 $ QR $ 分解中的 $ Q $ 因子, 其形式为 $ A=\widetilde{Q} \widetilde{R} $, 其中 $ \widetilde{Q} \in \mathrm{St}(m, d) $, $ \widetilde{R}\in \!\!\mathbb{R}^{\!\!d \times d} $ 为具有严格正对角元素的上三角矩阵.

对 $ \forall\left(\eta_1,\xi_1 \right),\left(\eta_2,\xi_2 \right) \in \mathcal{T}_{(Q, P)} S t(m, d) \times \mathcal{P} $, 基于切空间正交投影的向量转移定义为

其中

分别为 $ \eta_2 $ 在点 $ \mathcal{R}_Q\left(\eta_1\right) $ 处切平面 $ \mathcal{T}_{\mathcal{R}_Q\left(\eta_1\right)} $ 上的正交投影和 $ \xi_2 $ 在点 $ \mathcal{R}_P\left(\xi_1\right) $ 处切平面 $ \mathcal{T}_{\mathcal{R}_P\left(\xi_1\right)} $ 上的正交投影. 易知基于切空间正交投影的向量转移算子满足 Ring-Wirth 非扩张条件^[36]

接下来推导问题 (1.7) 中目标函数 $ f $ 关于 $ Q, P $ 的黎曼梯度和黎曼海塞具体计算公式. 为此定义映射 $ \bar{f}: \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} \rightarrow\!\! \mathbb{R} $

易知 $ f(Q, P) $ 是 $ \bar{f}(Q, P) $ 在乘积流形 $ \mathrm{St}(m, d) \times \mathcal{P} $ 上的限制函数.

引理 2.1 $ f $ 在 $ (Q, P) \in \mathrm{St}(m, d) \times \mathcal{P} $ 处的黎曼梯度

证 因为 $ \mathrm{St}(m, d) \times \mathcal{P} $ 是欧式空间 $ \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} $ 的嵌入子流形, 目标函数 $ f $ 关于 $ (Q, P) $ 的黎曼梯度等于 $ \bar{f} $ 关于 $ (Q, P) $ 的欧式梯度在切空间 $ \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} $ 上的正交投影. 基于迹微分并通过简单计算可知 $ \bar{f} $ 关于 $ Q $ 和 $ P $ 处的欧式梯度分别为

故 $ \bar{f} $ 在 $ (Q, P) \in \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} $ 的欧式梯度可表示为

利用切空间 $ \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} $ 上的正交投影表达式 (2.2)-(2.3), 得

证毕.

引理 2.2 $ \forall(Q, P) \in \mathrm{St}(m, d) \times \mathcal{P} $ 和 $ (\eta, \xi) \in \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} $, $ f $ 在 $ (Q, P) $ 的黎曼海塞为切空间 $ \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} $ 上的线性变换, 且

证 $ \forall(\eta, \xi) \in \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} $, 经简单计算 $ \bar{f} $ 关于 $ (Q, P) \in \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} $ 的欧式海塞

结合 $ \nabla^2 \bar{f} $ 和切空间 $ \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} $上的正交投影公式 (2.2)-(2.3), $ f $ 关于 $ (Q, P) $的黎曼海塞可通过如下方式计算^[37]

注意到 $ \operatorname{grad} f(Q, P)=\mathbf{P}_{(Q, P)}(\nabla \bar{f}(Q, P)) $, 参考文献 [37], (2.17) 式可进一步表示为

(2.18) 式的最后一个等式中用到了 $ \mathbf{P}_{(Q, P)}^2=\mathbf{P}_{(Q, P)} $. 又因为

注意到若 $ S $ 为 $ p \times p $ 阶对称矩阵, 则有

上式可以简化 (2.18) 式中 $ Q $ 因子部分的正交投影计算. 事实上结合上式可得

将 (2.19) 式代入 (2.18) 式, 并结合 (2.20) 式, 可得 $ \mathrm{Hess} f(Q, P)[(\eta, \xi)] $ 作用于 $ (\eta, \xi) $ 的表达式

将 (2.16) 和 (2.12) 式代入 (2.21) 式可得 (2.15) 式.

给定当前迭代点 $ x_k \in \mathcal{M} $, 黎曼优化通常按如下方式计算更新迭代点

其中 $ \eta_k $ 为 $ x_k \in \mathcal{M} $ 所对应切平面 $ \mathcal{T}_{x_k} \mathcal{M} $ 上的搜索方向, $ \mathcal{R} $ 表示 $ \mathcal{T}_{x_k} \mathcal{M} \rightarrow \mathcal{M} $ 的收缩映射. 注意到迭代格式 (3.1) 需要三个要素: 步长 $ \alpha_k>0 $, 搜索方向 $ \eta_k \in \mathcal{T}_{x_k} \mathcal{M} $ 和一个保证下一个迭代点是可行点的收缩映射, 也即 $ x_{k+1} \in \mathcal{M} $. 黎曼线搜索方法通过迭代的形式构造一个可行点序列 $ \left\{x_k\right\} $, 并希望该序列可以收敛到问题的局部极小点或者至少收敛到一个平稳点. 合适步长的选择对线搜索方法的鲁棒性和迭代效率至关重要. 为了保证目标函数值的减小, 关键是选择一个合适的步长, 使其既不能太大也不能太小. 目前常用的步长选取方法包括单调线搜索和非单调线搜索. 常用的单调线性搜索包括 Armijo 方法, 强 (弱) Wolfe 方法和 Goldstein 方法等^[38], 而常用的非单调搜索技术包括在文献 [39] 中引入的基于全局化策略的 Max 型非单调线搜索和文献 [34] 引入的 Zhang-Hager 非单调搜索技术.

本文将 Zhang-Hager 技术与文献 [40] 提出的 Armijo 型线搜索相结合, 针对本文具体模型, 按如下方式选取步长: 给定 $ {\rho _1}\in ( {0,1} ) $, $ {\rho _2}>0 $ 和 $ \tau \in[0,1) $, 选择步长 $ \alpha_k=\bar{\alpha}_k \rho^{h_k} $, 其中 $ \bar{\alpha}_k $ 为当前迭代步 $ \left(Q_k, P_k\right) $ 对应的试验步长, $ h_k $ 为满足下列不等式的最大整数

其中迭代参考值 $ C_k $ 是 $ C_{k-1} $ 和 $ f\left(Q_k, P_k\right) $ 的凸组合, 即

而 $ O_k=\tau O_{k-1}+1, O_0=1, C_0=f\left(Q_0, P_0\right) $.

对于不等式 (3.2) 中的步长 $ {\alpha _k} $, 首先说明其存在性, 即对 $ \forall {\rho _1}\in ( {0,1} ) $, $ {\rho _2}>0 $ 及 $ \forall k \geqslant 1 $, 存在 $ {\alpha}>0 $ 满足不等式

事实上, 由 $ {f\big({\mathcal{R}_{(Q_k, P_k)}}({\alpha}(\eta _k, \xi _k))\big)} $ 的一阶泰勒展开式^[35]

结合下文引理 4.3 的结论 $ f(Q_k, P_k)\leq C_k, \forall k\geq 0 $, 有

由极限保号性, 存在 $ \breve{\alpha}>0 $, 当 $ \alpha\in (0, \breve{\alpha}) $ 时, (3.3) 式成立.

结合上文中给出的乘积流形收缩映射、向量转移具体计算公式, 目标函数黎曼梯度及非单调线搜索公式, 下面给出求解问题 (1.7) 的一类非单调黎曼非线性共轭梯度法的具体迭代格式.

算法 1 求解问题 (1.7) 的黎曼非线性共轭梯度法

给定初始点 $ \left(Q_0, P_0\right) \in \mathrm{St}(m, d) \times \mathcal{P} $, 参数 $ 0<\mu_k<\mu_{\max }, 0<\alpha_m<\alpha_M<\infty $, $ \rho_1, \varepsilon, \rho\in (0,1), \rho_2>0, \tau \in [0,1), O_0=1, C_0=f\left(Q_0, P_0\right),\left(\eta_0, \xi_0\right)=-\operatorname{grad} f\left(Q_0, P_0\right), k:=0 $.

1. 当 $ \left\|\operatorname{grad} f\left(Q_k, P_k\right)\right\|>\varepsilon $ 时, 执行下面的步骤.

2. 选择 $ \bar{\alpha}_k \in\left[\alpha_m, \alpha_M\right] $, 计算最小正整数 $ h_k $ 使得步长 $ \alpha_k=\bar{\alpha}_k \rho^{h_k} $ 满足

3. 更新

4. 令

其中

5. 更新 $ O_{k+1}=\tau O_k+1 $ 和

6. 令 $ k\leftarrow k+1 $.

注 3.1 由 (3.7) 式中参数 $ {\mu _k} $ 构成的序列 $ \{\mu_k\} $ 是一个正实数有界序列, 即对 $ \forall k $, 都有 $ 0 < {\mu _k} \le {\mu _{\max }} $, 其中 $ {\mu _{\max }} \in \mathbb{R} $. 在本文具体计算中, 序列 $ \{\mu_k\} $ 取为每次迭代的当前步长 $ \alpha_{k} $ 组成的序列 $ \{\alpha_k\} $, $ {\mu _{\max }} = \alpha_{0} $.

本节给出算法 1 的全局收敛性分析. 记 $ \mathcal{T} \mathrm{St}(m, d) \times \mathcal{P} $ 为乘积流形 $ \mathrm{St}(m, d) \times \mathcal{P} $ 上的切向量从. 对 $ \forall(\eta, \xi) \in \mathcal{T} \mathrm{St}(m, d) \times \mathcal{P} $, 定义回调映射

记 $ \widehat{f}_{(Q, P)} $ 为 $ \widehat{f} $ 在 $ {(Q, P)} $ 处切空间 $ \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} $ 上的限制, 即

由文献 [35, p56] 可知, $ f $ 的黎曼梯度与其回调函数 $ \widehat{f} $ 的欧式梯度有如下关系

其中 $ 0_{(Q, P)} $ 为切空间 $ \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} $ 的原点.

引理 4.1 对 $ \forall\left(Q_0, P_0\right) \in \mathrm{St}(m, d) \times \mathcal{P} $, 水平集

是紧集.

证 $ \forall\left(Q_0, P_0\right) \in S t(m, d) \times \mathcal{P} $. 对 $ \forall(Q, P) \in \mathcal{Z} $, 有 $ \|Q\|=\sqrt{\operatorname{tr}\left(Q^T Q\right)}=\sqrt{d}. $ 又由

若记 $ P \in\!\! \mathbb{R}^{\!\!d \times m}(m \geq d) $ 的奇异值为 $ \delta_1\geq \delta_2\geq \cdots\geq \delta_d\geq 0 $, $ Q^{\mathrm{T}}X^TFX \in\!\! \mathbb{R}^{\!\!d \times m} $ 的奇异值 $ \gamma_1\geq\gamma_2\geq \cdots \gamma_d\geq 0 $, 由文献 [41] 中 Neumann 不等式的推论 6.4.3 及柯西-施瓦茨不等式有

又由 $ \psi>0 $ 及 $ D $ 为具有非负对角元的对角阵可知

故有

$ \forall(Q, P) \in \mathcal{Z} $, 有$ f(Q, P) \leq f\left(Q_0, P_0\right) $, 即

上式左边为关于 $ \|P\| $ 的开口向上的二次函数, 而 $ f\left(Q_0, P_0\right) $ 为有限值, 故 $ \|P\| $ 的取值一定是有界的. 因此水平集 $ \mathcal{Z} $ 是有界的, 又目标函数 $ f(Q, P) $ 关于 $ Q, P $ 是连续的, $ \mathcal{Z} $ 是闭集, 从而水平集 $ \mathcal{Z} $ 是紧集.

由于 $ \mathrm{St}(m, d) \times \mathcal{P} $ 是 $ \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} $ 的嵌入黎曼子流形, 且对 $ \forall(Q, P) \in \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} $ 都有 $ \mathcal{T}_{(Q, P)} \mathrm{St}(m, d) \times \mathcal{P} \subset \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} $, 故 $ \operatorname{grad} f(Q, P) $ 可以看作是 $ \mathrm{St}(m, d) \times \mathcal{P} $ 到 $ \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} $ 的一个连续非线性映射, 由引理 4.1 可知 $ \mathcal{Z} $ 是紧集, 故存在常数 $ \kappa>0 $ 使得

另外, 对 $ \forall\left(Q_1, P_1\right),\left(Q_2, P_2\right) \in \mathrm{St}(m, d) \times \mathcal{P}, \operatorname{grad} f\left(Q_1, P_1\right) $ 和 $ \operatorname{grad} f\left(Q_2, P_2\right) $ 可以看作是 $ \mathbb{R}^{m \times d} \times \mathbb{R}^{d \times m} $ 的向量, 故 $ \operatorname{grad} f\left(Q_1, P_1\right)-\operatorname{grad} f\left(Q_2, P_2\right) $ 是有意义的, 又因 $ \mathcal{Z} $ 是紧集, 故 $ \operatorname{grad} f(Q, P) $ 在 $ \mathcal{Z} $ 上 Lipschitz 连续, 即存在常数 $ \beta_L $ 使得

其中 “dist” 表示 $ \mathrm{St}(m, d) \times \mathcal{P} $ 上的黎曼距离[35,p46].

引理 4.2 存在非负常数 $ c_1, c_2 $ 使得对 $ \forall k $, 有

证

此时 $ c_1=1 $. 另一方面, 根据基于正交投影的向量转移算子的非扩张性和柯西-施瓦茨不等式得

故可得

此时 $ c_2=\mu_{\text {max }}+1 $, 即引理得证.

下面给出算法 1 的全局收敛性, 为此先建立序列 $ \left\{C_k\right\} $ 的若干重要性质.

引理 4.3 令 $ \left\{\left(Q_k, P_k\right)\right\} $ 为算法 1 生成的有限序列, 有

此外, 序列 $ \left\{C_k\right\} $ 是单调递减的.

证 定义函数 $ \psi_{k+1}: \mathbb{R}\!\! \rightarrow\!\! \mathbb{R}\!\!$,

则 $ \psi_{k+1}(t) $ 关于 $ t $ 的导数为

从引理 4.2 和非单调 Armijo 类条件可知

这意味着对于所有的 $ t \geq 0, \psi_{k+1}^{\prime}(t) \geq 0 $. 因此, 对所有 $ t \geq 0 $,

取 $ t=\tau O_k $ 有

另一方面, 由算法 1 和 (4.7) 式有

因此序列 $ \left\{C_k\right\} $ 是单调递减的.

引理 4.4 在算法 1 中, 当 $ k $ 足够大时, 存在一个常数 $ v>0 $ 使得步长 $ \alpha_k $ 满足

证 由 Zhang-Hager 条件和算法 1 可知

又有

令两边取极限, 可得

(4.15) 式的第二个极限意味着存在 $ N_\alpha \in N $ 使得 $\delta^{-1} \alpha_k\left\|\left(\eta_k, \xi_k\right)\right\| \leq \kappa, \forall k \geq N_\alpha$. 其中 $ \kappa $ 由 (4.5) 式确定.

设 $ k $ 为任意正整数使 $ k \geq N_\alpha $, 为证明该引理分析两种情况: 如果在第 $ k $ 次迭代中 $ \tilde{\alpha}_k $ 没有被改变, 那么有 $ \alpha_k=\tilde{\alpha}_k \geq \alpha_m>0 $; 另一种可能是标量 $ \tilde{\alpha}_k $ 不满足非单调 Armijo 条件, 在这种条件下$ \alpha_k=\delta^{m_k} \tilde{\alpha}_k $ 其中 $ m_k \geq 1 $ 是使 Armijo 条件成立的最小整数, 因此对于 $ \delta^{-1} \alpha_k $, Zhang-Hager 不等式不成立, 有

结合引理 4.3 可得

结合中值定理, 柯西-施瓦茨不等式以及 (4.17) 式可知, 存在一个 $ \theta_k \in(0,1) $ 使得当 $ k $ 足够大时

结合 (4.17) 式和引理 4.2 有

因此, 当 $ k $ 足够大且 $ v=\min \left\{\alpha_{\text {min }}, \frac{\left(1-\rho_1\right) \delta c_1}{\left(\beta_L+\rho_2\right) c_2^2}\right\} $ 时, 引理成立.

定理 4.1 令 $ \left\{\left(Q_k, P_k\right)\right\} $ 是由算法 1 产生的迭代序列, 则有

证 根据 (4.15) 式中的第一个极限和 (4.7) 式有

令 $ \varepsilon>0 $ 为任意的正数, 根据 (4.19) 式, 存在 $ K \in N $, 使得对于所有 $ k>0 $ 有

其中 $ v $ 由引理 4.4 确定. 选择 $ N_{\varepsilon}=\max \left\{K, N_\alpha\right\} \in N $, 对所有 $ k \geq N_{\varepsilon} $ 可得

这意味着对所有 $\left\|\operatorname{grad} f\left(Q_k, P_k\right)\right\|^2<\varepsilon$. 因此定理成立.

本节利用数值实验和数值比较验证算法 1 对于求解问题 (1.7) 的有效性. 所有的数值结果均通过 Matlab(R2022a), $ \text{Intel}^{\circledR} $ Core i5 处理器, 3.00GHz 的 PC 中获得. 首先给出本节数值实验中的参数选取说明

(1) 关于 $ X, W, F, D $ 的选取. 对于数据矩阵 $ X\in \mathbb{R}^{N\times m} $, 其中 $ N $ 为训练样本量, $ m $ 为样本维度, 文献 [9] 采用 FERET 脸谱数据库中给出的数据集, 本文不失一般性通过 Matlab 随机生成 $ X={ {\rm rand}(N,m)} $, 即元素属于 $ (0,1) $ 满足均匀分布的 $ N\times m $ 随机数矩阵. 分两种情形来给出数据矩阵 $ X $, $ N\gg m $ 高样本量、低维样本; $ m\gg N $ 低样本量、高维样本. 因为近邻样本的数据点很可能具有相同的类别标签, 为建立局部几何流形结构, 文献 [9]构建一个类内相似图来定义$ W $, 其最近邻图模型定义为

其中 $ N_{K}(x_j) $ 为与样本点 $ x_i $ 相邻的同类样本点 $ x_j $ 子集. 因数据矩阵 $ X $ 通过随机方式生成, 不失一般性, 本文实验中同样按随机方式生成 $ W={ {\rm rand}(N,N)} $.进而通过 $ X $, $ W $ 计算 $ F $, $ D $, 即 $ F=G \odot W $, 其中 $ G_{i j}=\frac{1}{2\left\|x_{i}-x_{j} Q P\right\|_{2}} $, $ D $ 为对角矩阵且 $ D_{i i}=\sum_{j} F_{i j}. $

(2) 初始迭代矩阵. 本文算法及比较算法的迭代初值 $ (Q_0 $, $ P_0) $ 均取为随机生成的可行点,

其中 $ \textrm {randn}(d,m) $ 为元素服从标准正态分布的 $ d\times m $ 随机数矩阵, $ \textrm{orth()} $ 表示对括号内矩阵进行列标准正交化.

(3) 算法终止标准. 参考文献 [42] 中关于黎曼梯度类算法终止标准的说明, 算法 1 的终止标准取为: $ \left\| {\mathrm{grad} f\left( {{Q_k},{P_k}} \right)} \right\| \le \epsilon $ 或者 $ tol_{\left( {Q,P} \right)}^k \le {\epsilon_{\left( {Q,P} \right)}} $ 和 $ tol_f^k \le {\epsilon_f} $, 其中

其中参数 $ \epsilon, \epsilon_{(Q,P)},\epsilon_f $ 的选取为 $ \epsilon = 10^{-5} $, $ \epsilon_{(Q,P)}= 10^{-5} $, $ \epsilon_f= 10^{-8} $. 算法 1 中其它参数选取方式为 $ \delta_1 = 10^{-3} $, $ \delta_2 = 10^{-8} $, $ \rho = 0.5 $, $ \tau = 0.85 $, 最大迭代步设为 $ 10000 $.

(4) 初始步长. 不等式 (3.2) 中试验步长 $ \bar{\alpha}_k $ 的选取由如下方式确定

其中 $ \alpha^{BB} $ 为 Barzilai-Borwein(BB) 步长, 其定义为

其中 $ {M_{k - 1}} = ({Q_k},{P_k}) - ({Q_{k - 1}},{P_{k - 1}}) $, $ {Y_{k - 1}} = ({\eta _k},{\xi _k}) - ({\eta _{k - 1}},{\xi _{k - 1}}) $.

对于问题 (1.6), 在变量矩阵 $ F, D $ 固定的情况下, 文献 [9] 中设计了基于交替最小二乘思想的求解方案. 对于 $ (Q_k, P_k)\in \mathrm{St}(m, d) \times \mathcal{P} $, 其更新步的迭代框架为

对于 (5.3) 式中的 $ P $ 子问题 (无约束迹函数极值问题), 通过 $ \frac{\partial f(Q_k, P)}{\partial P}=0 $ 可得其精确解析表达式为

对于 (5.3) 式中的 $ Q $ 子问题, 其等价于

显然问题 (5.5) 关于约束变量 $ Q $ 并没有明确解析表达式. 文献 [9] 按如下方式获得 $ Q $ 子问题的近似解: 记 $ A_k=\psi I_d+Q_k^T X^T D X Q_k $, 将 (5.4) 代入问题 (5.5) 中目标函数, 同时取近似等式 $ A_k\approx \psi I_d+Q^T X^T D X Q $, 问题 (5.5) 经一步步简化可转化为如下极值问题

上述极值问题 (5.6) 的解可以通过如下特征值-特征向量分解求得

其中 $ \lambda $ 为特征向量 $ \nu $ 对应的特征值, 进而文献 [9] 将矩阵 $ \left(X^T D X+\alpha I\right)^{-1}\left(X^T F X X^T F^T X\right) $ 的前 $ d $ 个最大特征值所对应的特征向量按列排列, 并作正交化处理后得到的列正交矩阵作为问题 (5.6) 的最优解.

显然文献 [9] 求得的 $ Q $ 子问题近似解与变量 $ P $ 无关, 进而得出 $ (Q,P) $ 经初始迭代矩阵迭代一次后不再更新, 即目标函数值 $ f(Q,P) $ 经迭代一次后不再下降 (即使对文献 [9]中给出的 RDR 算法同时考虑更新变量 $ F $ 和 $ D $, 因 $ F,D $ 依赖于变量 $ Q,P $), 这与文献 [9, 图6] 给出的目标函数随迭代步的变化曲线图一致.

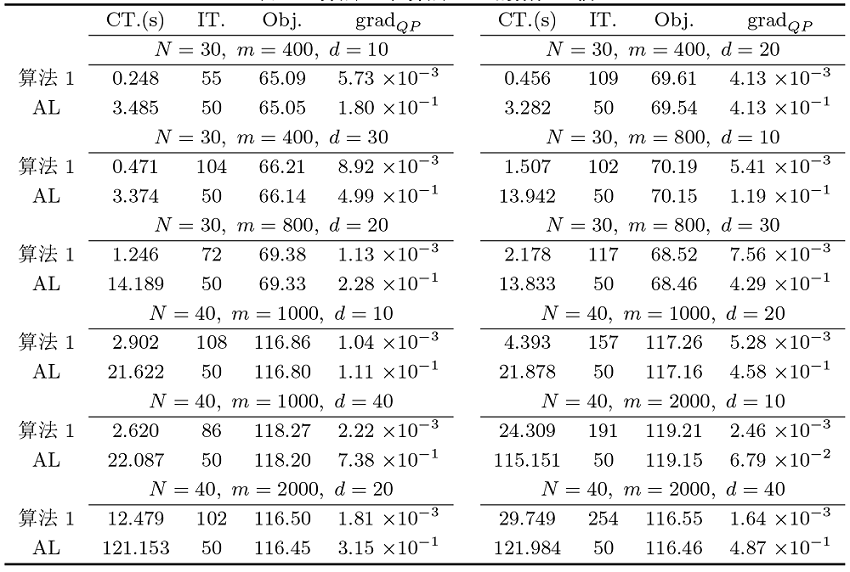
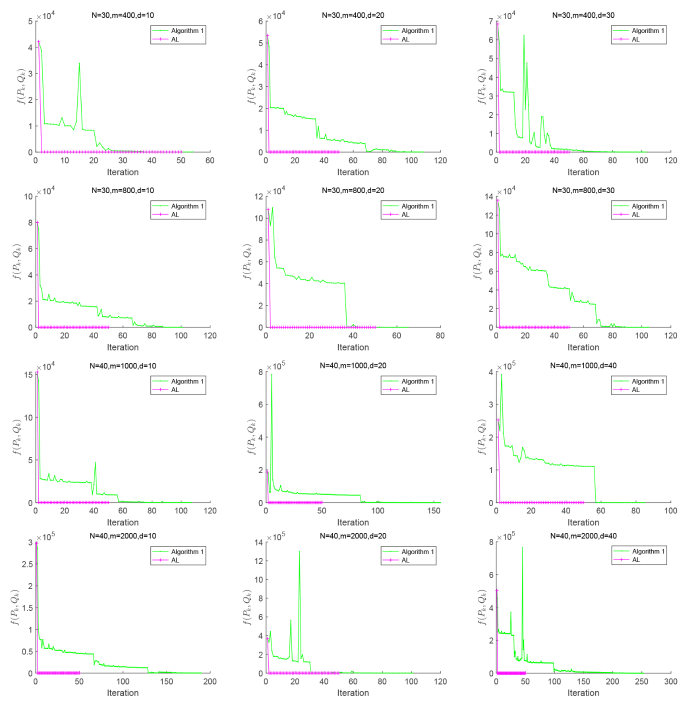
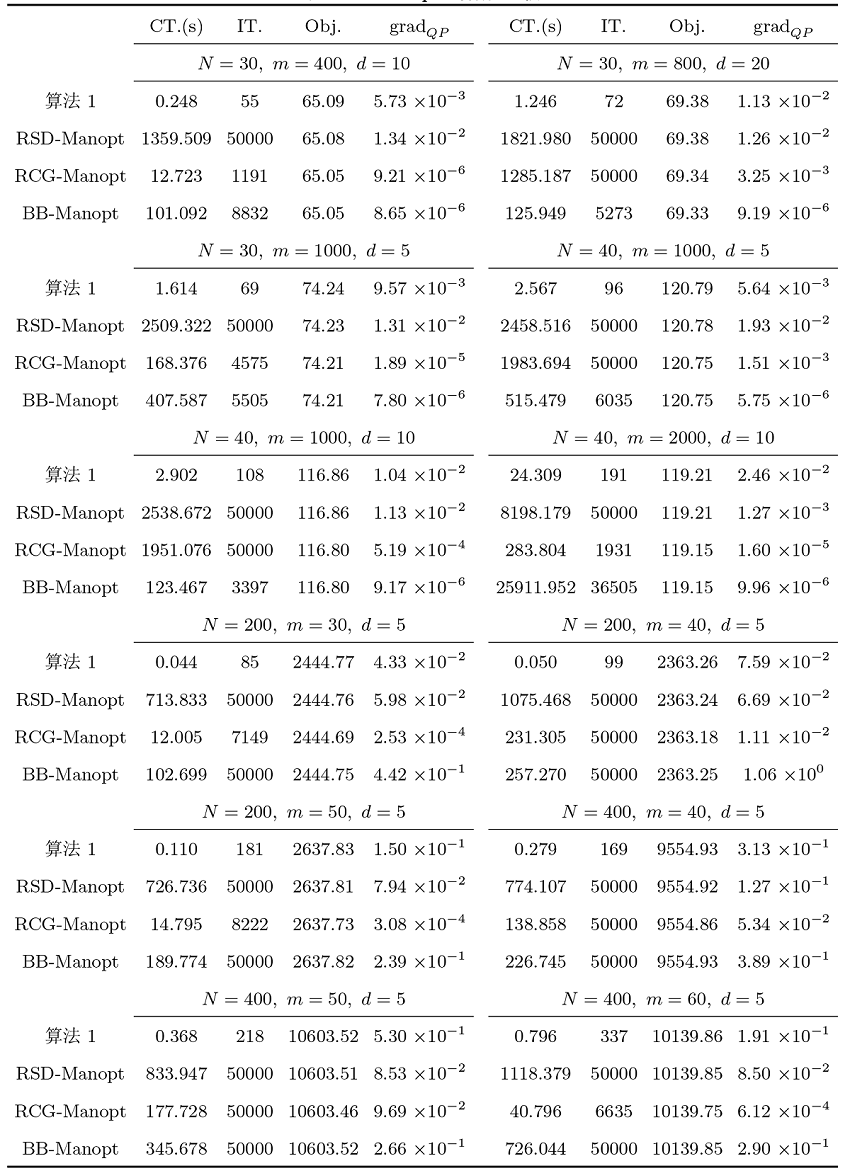
表1给出了算法 1 与文献 [9] 中近似交替最小二乘算法 (AL) 在不同系统维数下的数值比较结果, 其中算法 AL 的最大迭代步设置为 50. 表1 中“CT.” 和“IT.”分别表示迭代终止所需的计算时间和迭代次数 $ k $, ``Obj."和``$ {{\rm grad}_{QP}} $" 分别表示迭代终止对应的目标函数值 $ f(Q_k, P_k) $ 和黎曼梯度范数 $ \|\textrm{grad} f(Q_k, P_k)\| $. 图1给出了算法 1 与 AL 算法目标函数值随迭代步的变化曲线图. 从表1中可以看出, 算法 1 的单步计算成本远低于算法 AL, 虽然算法 1 给出的迭代终止目标函数值略高于算法 AL, 但从迭代终止的黎曼梯度范数来看, 算法 1 给出的近似解精度高于算法 AL. 从图1中也可以看出, 算法 AL 的目标函数值在迭代一次后不再下降, 这与前述分析一致.

本文提出的线搜索 (3.2) 实质上是结合了 Zhang-Hager 非单调线搜索技术与文献 [40] 中单调 Armijo 型线搜索的一种新型非单调线搜索. 为验证其有效性, 本节与前文提到的两种主流的非单调线搜索-Zhang-Hager线搜索技术和 Max 型非单调线搜索来进行比较. 与之比较的采用两类非单调搜索技术的代表性黎曼梯度类算法包括文献 [42] 中提出的应用于流形优化的基于曲线搜索的黎曼梯度下降法 ({OptStiefelGBB}), 文献 [32,43] 推广的基于欧式空间 Dai 非线性共轭梯度法且应用于流形优化的黎曼非线性共轭梯度法 ({RCG}). 首先给出算法 {OptStiefelGBB} 和 {RCG} 应用于求解问题 (1.7) 的迭代框架.

OptStiefelGBB: 对于给定参数 $ \delta, \rho, \vartheta \in \left( {0,1} \right) $ 和搜索方向 $ \left({{\eta _k},{\xi _k}}\right)=-\mathrm{grad} f(Q_k, P_k) $, 其搜索步长 $ {\alpha _k}=\max\{\bar{\alpha}_k {\rho ^h}, j=0,1,2,\cdots \} $ 由如下Zhang-Hager非单调搜索准则确定

其中作用于 Stiefel 流形上的收缩映射 $ \mathcal{R}_Q{(\alpha\eta)} $ 采用基于 Cayley 变换的收缩算子^[42], 初始迭代步长 $ \bar{\alpha}_k $ 的选取同 (5.1)-(5.2). 参考函数 $ C_{k} $ 的选取同算法 1.

RCG: 迭代步长 $ {\alpha_k} $ 采用如下 $ \textrm{Max} $ 型非单调线搜索确定

其中作用于 Stiefel 流形上的收缩映射 $ \mathcal{R}_Q{(\alpha\eta)} $ 同算法 {OptStiefelGBB}, $ \delta \in \left( {0,1} \right),{h_k} = \min \left\{ {h - 1,k} \right\} $, $ h $ 为正整数. 搜索方向更新方案为

其中 $ \mathbf{T} $ 为采用基于微分收缩的向量转移算子^[32], 参数 $ {\beta _{k + 1}} \in \left[ {0,\beta _{k + 1}^D} \right] $, 而

其中 $ M = \left\langle {\mathrm{grad} f\left( {{Q_{k + 1}},{P_{k + 1}}} \right),{\mathbf{T} _{{\alpha_k}\left( {{\eta _k},{\xi _k}} \right)}}\left( {{\eta _k},{\xi _k}} \right) - \left\langle {\mathrm{grad} f\left( {{Q_k},{P_k}} \right),\left( {{\eta _k},{\xi _k}} \right)} \right\rangle } \right\rangle $.

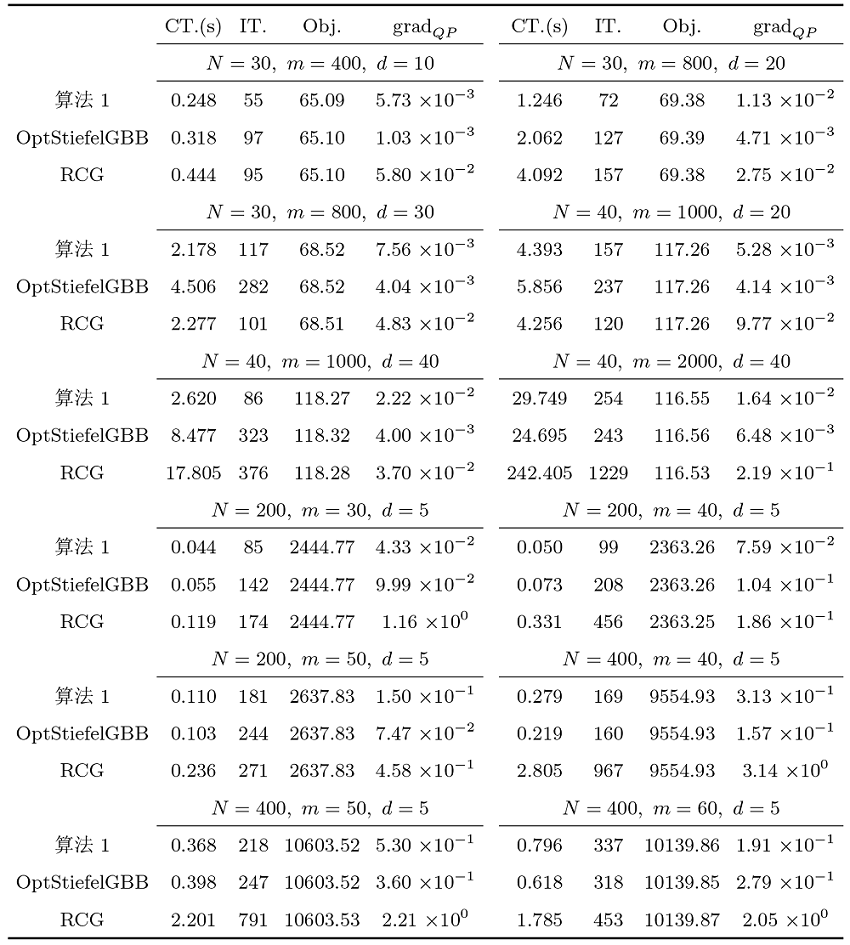
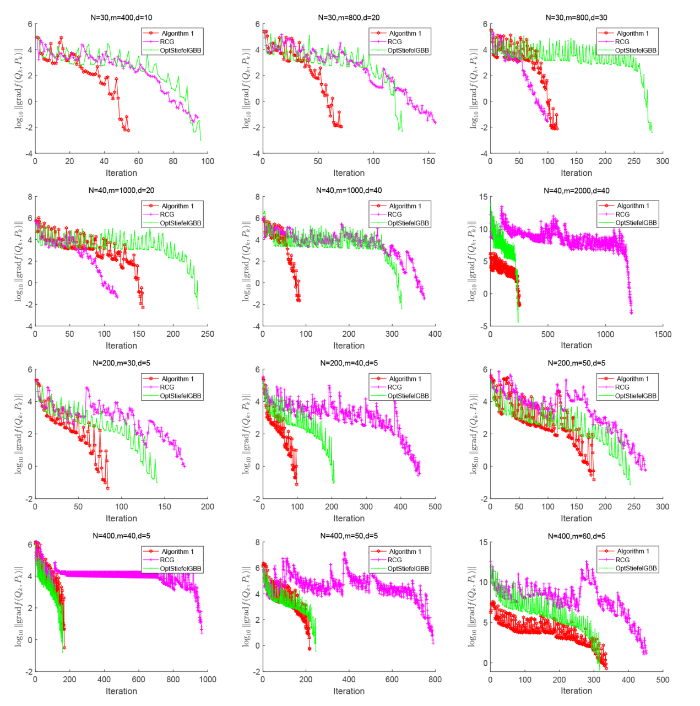
表2给出了不同系数维数下算法 1 与 OptStiefelGBB 和 RCG 的数值比较结果, 其中表头“CT.”、“IT.”、“Obj.”和“${ {\rm grad}_{QP}} $” 的定义同表1. 表2前 6 组数据给出的是低样本量、高维样本的数值比较结果, 后 6 组数据给出高样本量、低维样本的比较结果. 图2给出了三种算法的黎曼梯度范数随迭代步的半对数收敛曲线图. 从表2中数据可以看出, 在相同的终止标准下, 三种算法得到的迭代终止目标函数值近似相同, 其迭代解所对应的黎曼梯度范数相当. 但从迭代时间和迭代步来看, 大多数情况下, 本文算法 1 在迭代效率上有一定的优势. 因算法 OptStiefelGBB 不需要计算向量转移算子, 故达到相同终止标准所需要的迭代时间相对较少. 结合表2 的数据结果和图2的收敛曲线图可以看出, 本文提出的结合 Zhang-Hager 非单调线搜索技术与文献 [40] 中单调 Armijo 型线搜索的新型非单调线搜索较两类主流的非单调线搜索在迭代效率上有一定的优势.

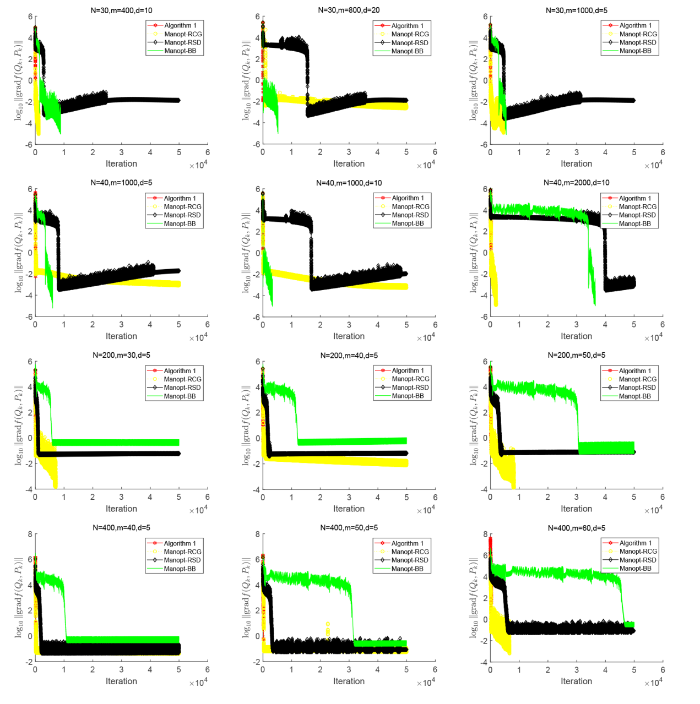
本小节给出算法 1 与黎曼优化工具箱 Manopt^[44] 中已有的一阶方法进行数值比较, 与之比较的算法包括 Steepest-descent(RSD-Manopt), Conjugate-gradient(RCG-Manopt) 和 Barzilai-Borwein(BB-Manopt). 表3给出了在低样本量高维样本和高样本量低维样本两种情况下四种算法的数值比较结果. 图3给出了四种算法的黎曼梯度范数随迭代步的半对数变化曲线图. 黎曼优化工具箱 Manopt 中的三类算法其相关参数选取和终止标准均取为默认, 最大迭代步修改为 50000. 从表3中数据和图3中黎曼梯度范数的变化曲线图可以看出, 算法 RSD-Manopt 和算法 BB-Manopt 在大多数情况下都达到最大迭代步, 其黎曼梯度范数下降相对比较缓慢, 且达到一定精度后趋于稳定. 由此可以看出, 对于求解问题 (1.7), 本文算法较黎曼优化工具箱 Manopt 中的一阶算法相比也具有一定的优势.

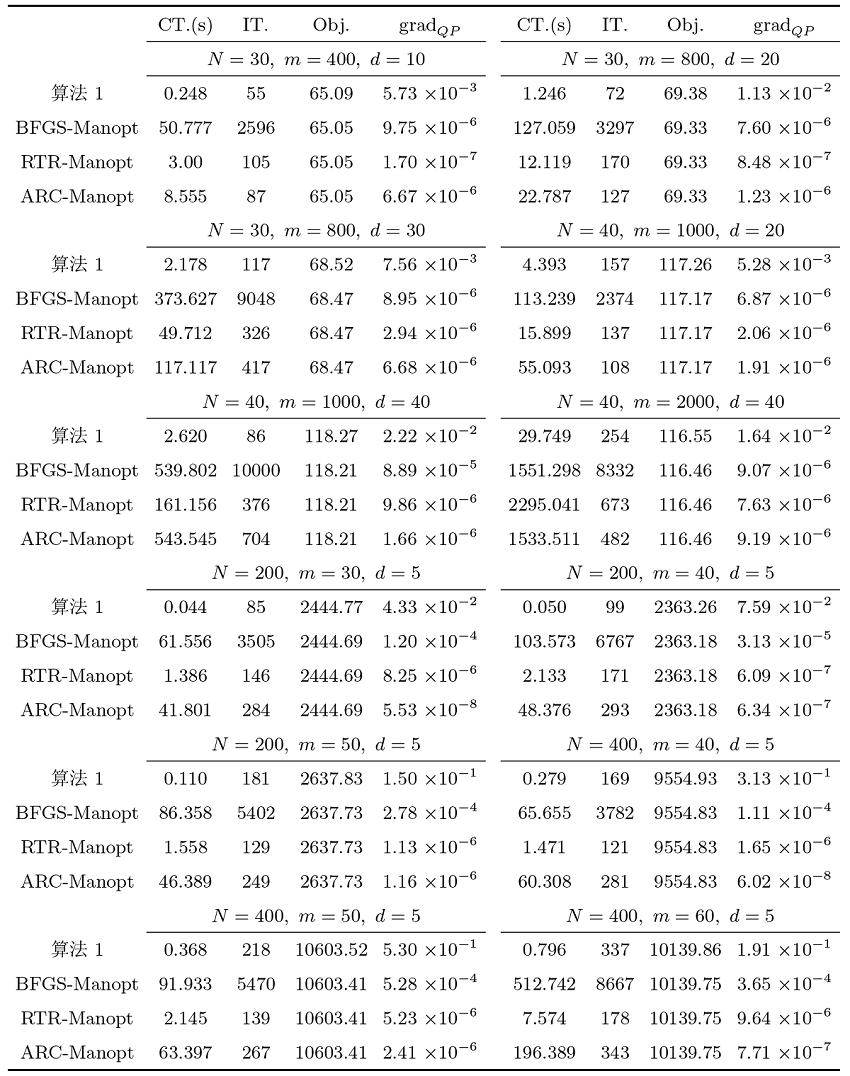
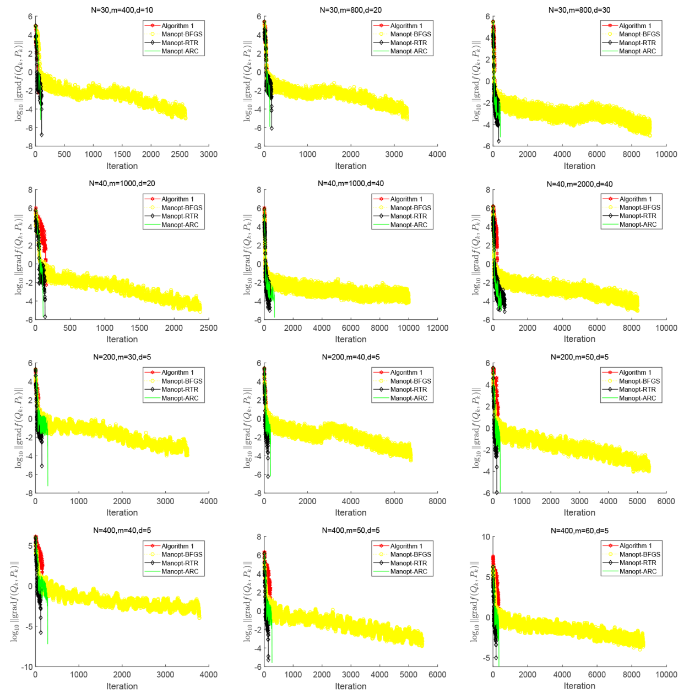
基于引理 2.2 中给出的黎曼海塞具体计算公式 (2.15), 本小节给出算法 1 与黎曼优化工具箱 Manopt 中已有的二阶算法进行数值比较, 与之比较的算法包括 BFGS(BFGS-Manopt), Trust-regions(RTR-Manopt) 和 Adaptive regularization by cubics(ARC-Manopt). 表4给出了在低样本量高维样本和高样本量低维样本两种情况下四种算法的数值比较结果. 图4给出了四种算法的黎曼梯度范数随迭代步的半对数变化曲线图. 黎曼优化工具箱 Manopt 中的三类算法其相关参数选取和终止标准均取为默认, 最大迭代步修改为 10000. 从表4的数据可以看出, 在对应的终止标准下, 算法 1 虽然总体迭代步数较多, 但因为不需要内迭代, 故总体时间较少. 算法 RTR-Manopt 因为需要用到截断共轭梯度法 (tCG) 求解相应信赖域子问题, 虽然具有超线性收敛速度, 但是总体迭代时间要比算法 1 长. 另在大多数情况下, 算法 BFGS-Manopt 的总体运行时间最长, 这是因为黎曼优化工具箱中的黎曼 BFGS 算法实质上是 Limited-memory BFGS 在黎曼流形上的推广, 且其默认的记忆规模为 30, 也即每次迭代中都需计算 30 次基于正交投影的向量转移算子, 这很大程度上主导了BFGS-Manopt 的运行时间.

本文研究了来源于特征提取的一类鲁棒判别回归模型, 该模型可重构为由 Stiefel 流形和线性流形所组成的黎曼乘积流形上的一类矩阵迹函数极小化问题, 即问题 (1.6). 因模型 (1.6) 的目标函数中矩阵 $ F, D $ 的元素由变量 $ Q, P $ 确定, 故原问题难以求解. 本文考虑其取为固定矩阵时的简化版本, 即问题(1.7). 结合 Zhang-Hager 非单调搜索技术和 Armijo 型线搜索, 本文提出一类新的非单调搜索准则, 并结合乘积流形几何性质, 构造一类适用于求解问题 (1.7) 的黎曼非线性共轭梯度法, 同时给出了算法的全局收敛性分析. 充分的数值实验和数值比较说明了本文算法对于求解问题 (1.7) 的可行性和高效性, 其中数值比较包括与已有的近似交替最小二乘方法的比较, 与现有两类主流非单调线搜索技术的比较, 以及黎曼优化工具箱 Manopt 中已有的一阶和二阶方法的比较. 数值结果表明本文针对问题 (1.7) 所提出的算法, 与已有算法相比, 在迭代解精度、迭代时间或迭代步数上都具有一定的优势.

本文只针对问题 (1.7) 进行数值求解, 如何设计有效算法进一步求解问题 (1.6) 是下一步的研究工作, 可行的研究方案是采用交替更新的迭代思想, 其迭代框架为

1. 给定数据矩阵 $ X $ 和描述数据集局部流形结构的类内相似图 $ W $. 给定初始点 $ \left(Q_0, P_0\right) \in \mathrm{St}(m, d) \times \mathcal{P} $, $ k:=0 $;

2. $ k=1,2,\cdots $, 直到满足终止标准;

3. 生成 $ F_k, D_k $;

4. 通过算法1更新 $ (Q_k, P_k) $, 即

但终止标准的建立和算法的收敛性分析值得进一步研究.